让我们回归机器学习的算法部分。这篇BLOG我们将会一同学习加速我们算法的有一个常用技巧-参数向量化,特别感谢大佬的推导思路。
为什么要参数向量化
为什么我们要参数向量化呢?
首先,无论我们是用Octave 还是别的语言,比如MATLAB Python NumPy 或 Java C C++ 所有这些语言都具有各种方便的线性代数库,这些库文件通常都是内置的,且已经经过高度优化,这为我们的参数向量化提供了物质基础。这些库函数通常是数值计算方面的专业人士开发的,而当我们实现机器学习算法时,如果能好好利用这些线性代数库而不是自己去做那些函数库可以做的事情的话,往往程序的运行速度会更快, 并且能够更好地利用你的计算机里可能有的一些并行硬件系统。
其次,这也意味着我们可以用更少的代码来实现你需要的功能 并且实现的方式更简单,代码出现问题的有可能性也更小。比如与其自己写代码,在Octave中做矩阵乘法 ,只需要输入 a * b 就可以了。 就是一个非常高效的两个矩阵相乘的程序。还有很多例子可以说明,如果你用合适的参数向量化方法来实现,你就会有一个简单得多也有效得多的代码。所以我们提倡参数向量化。
假设函数h(x)的参数向量化
让我们看看线性回归中的假设函数如何使用参数向量化吧。首先,假设函数 h(x) 可以写成求和的形式:
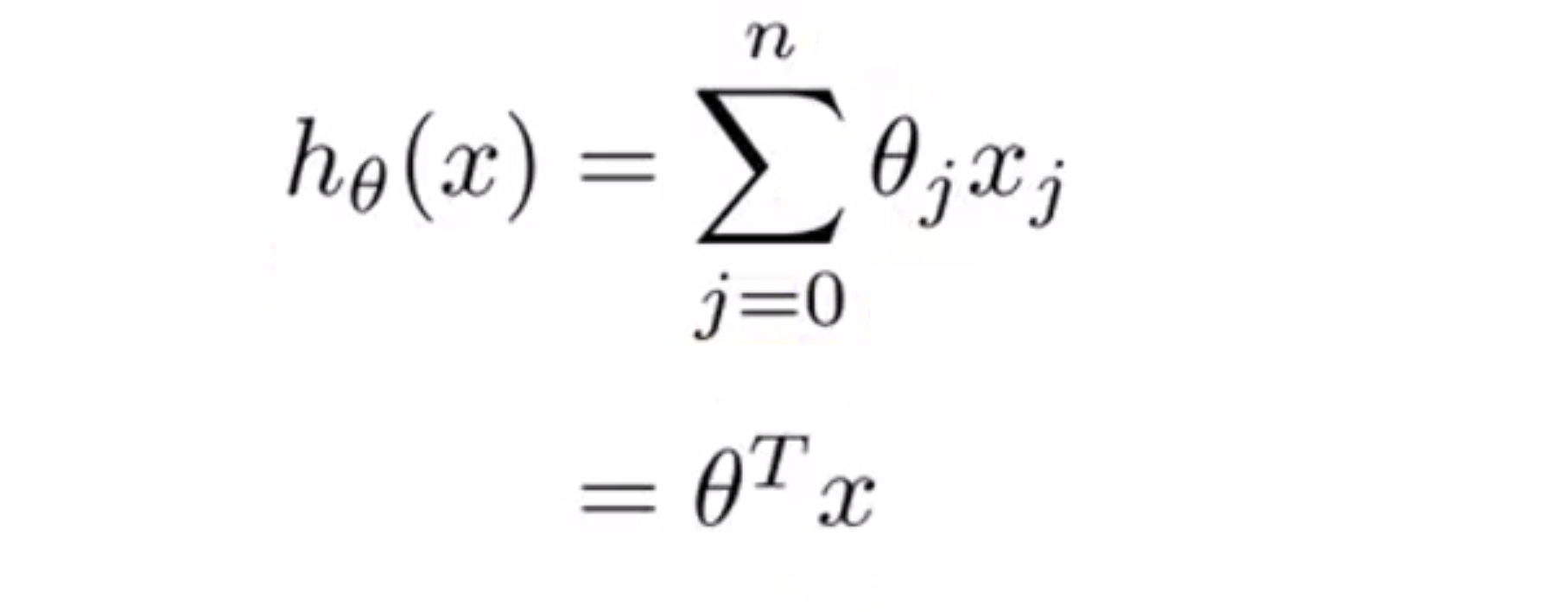
如果我们想要直接计算 h(x) ,我们就要使用循环语句去计算 j = 0 到 j = n 的和。但换另一种方式来想想,如果我们把 h(x) 看作 θ^T x 那么,h(x)就可以写成两个向量的内积,这两种思考角度会给你两种不同的实现方式。
比如说,下面是在Octave中未向量化的代码实现方式,我们首先要初始化变量 prediction 的值为0.0 ,然后变量 prediction 的最终结果就是 j 取值 0 到 n+1 循环,变量 prediction 每次都通过 自身加上 θ(j) x(j):

顺便要提醒一下,这里的向量,用的下标是 0 所以我们有 θ0 θ1 θ2,但因为 Octave 的下标从1开始,所以 θ0 我们就要用 theta(1) 来表示,所以这里我的 for 循环 j 取值从 1 直到 n+1 而不是 从 0 到 n。
接下来是参数向量化后的代码实现,我们把 x 和 θ 看做向量,这样就只需要令变量 prediction 等于 theta 的转置乘以 x 就可以计算出来了:
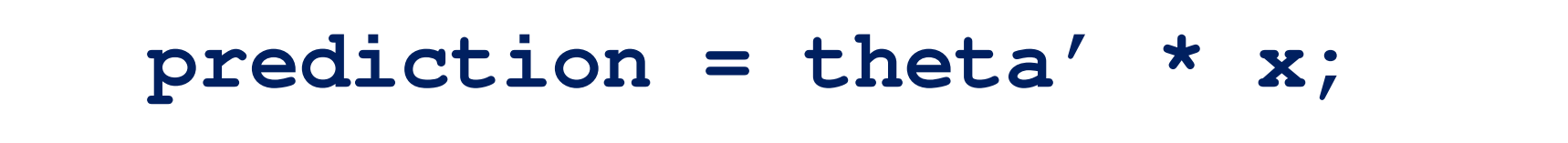
对比写前面很多行的 for 循环的代码,参数向量化后你只需要一行代码,而这行代码还利用了 Octave 的高度优化的线性代数算法来计算两个向量的内积。这样向量化的实现不仅仅是更简单,运行起来也将更加高效。这就是在 Octave 上所做的。
而向量化的方法在其他编程语言中同样可以实现,让我们来看一下 C++ 上的例子,下面是未向量化的代码实现的样子:

我们再次初始化变量 prediction 为 0.0 ,然后我们现在从 j 等于 0 到 n 进行循环,每次变量 prediction += theta[j] * x[j],这往往是低效的。
而使用一个比较好的 C++ 数值线性代数库,你就可以用下面这个方程来写这个函数,而代码取决于你的数值线性代数库的内容:

你可以有一个对象 (object) 比如这个 C++ 对象 theta 和另一个一个 C++ 对象向量 x ,这时只需要用 theta.transpose ( ) * x 。根据你所使用的 数值和线性代数库的使用细节的不同,你最终使用的代码表达方式可能会有些许不同,但是通过参数向量化后,使用一个库来做内积,你可以得到一段更简单更高效的代码。
梯度下降更新的参数向量化
接下来让我们来看一个更为复杂的例子-梯度下降的更新。下图是我们熟悉的更新规则,我们用这条规则对 j 等于 0 1 2 ……的所有值更新:
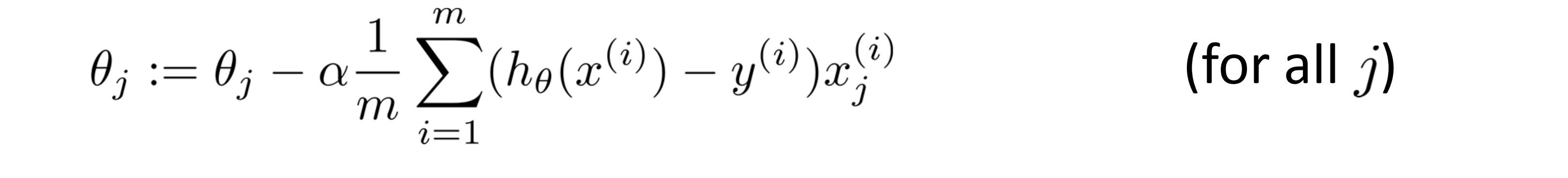
为了简化问题,我们假设只有两个特征量,所以此时 n 等于 2。下图是我们需要做的我们需要对 θ0 θ1 θ2 进行更新,这些都应该是同步更新:
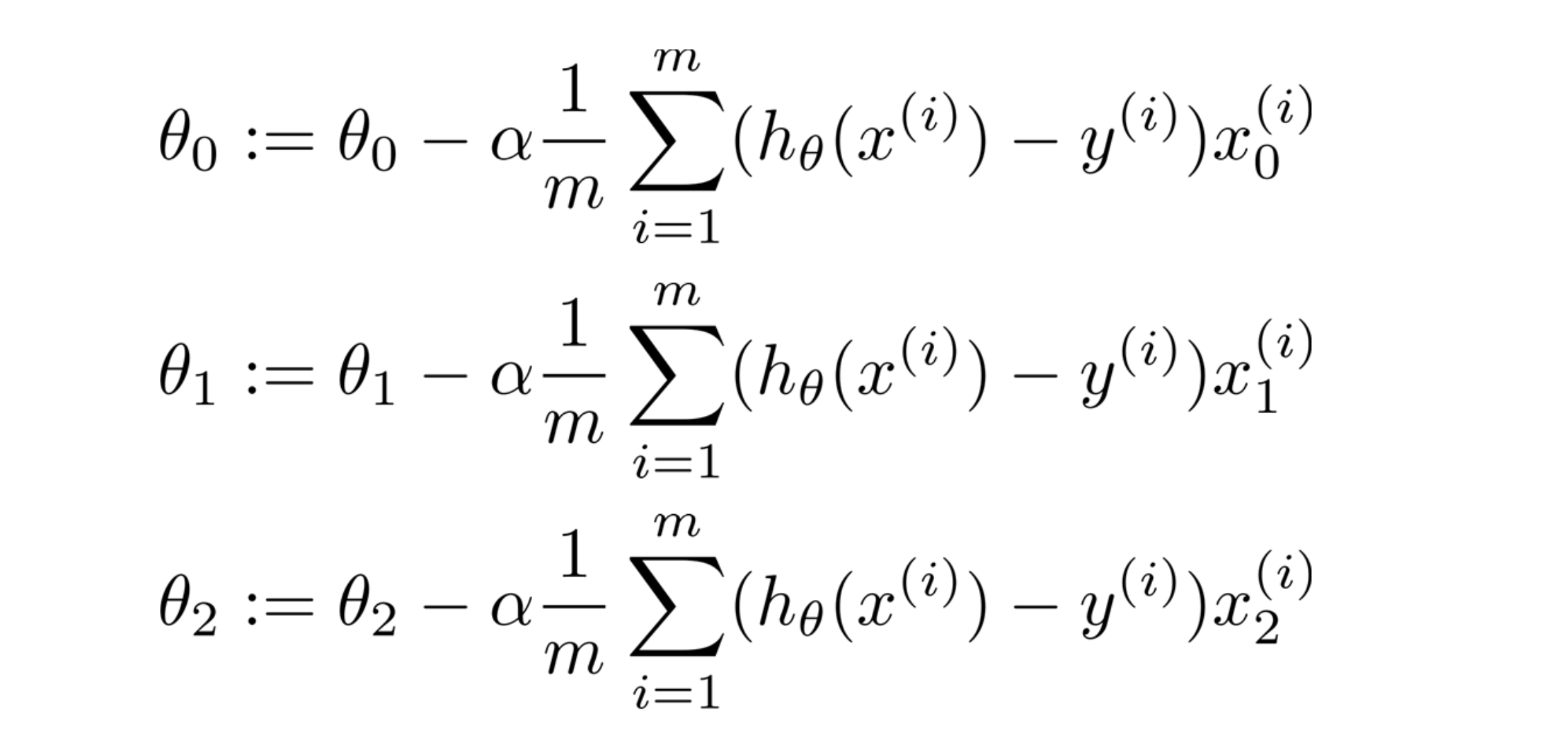
当然我们也可以使用for循环逐个进行更新,但我们应该看看是否可以拿出一个向量化的代码实现。
首先我们要对我们 θ 的更新进行改写:
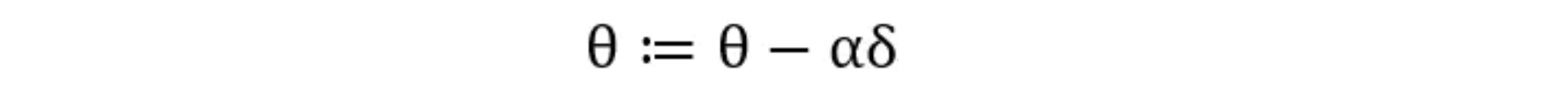
其中 α 仍为学习速率,是一个实数,而 θ 和 δ 都是一个n+1 维的向量,为:
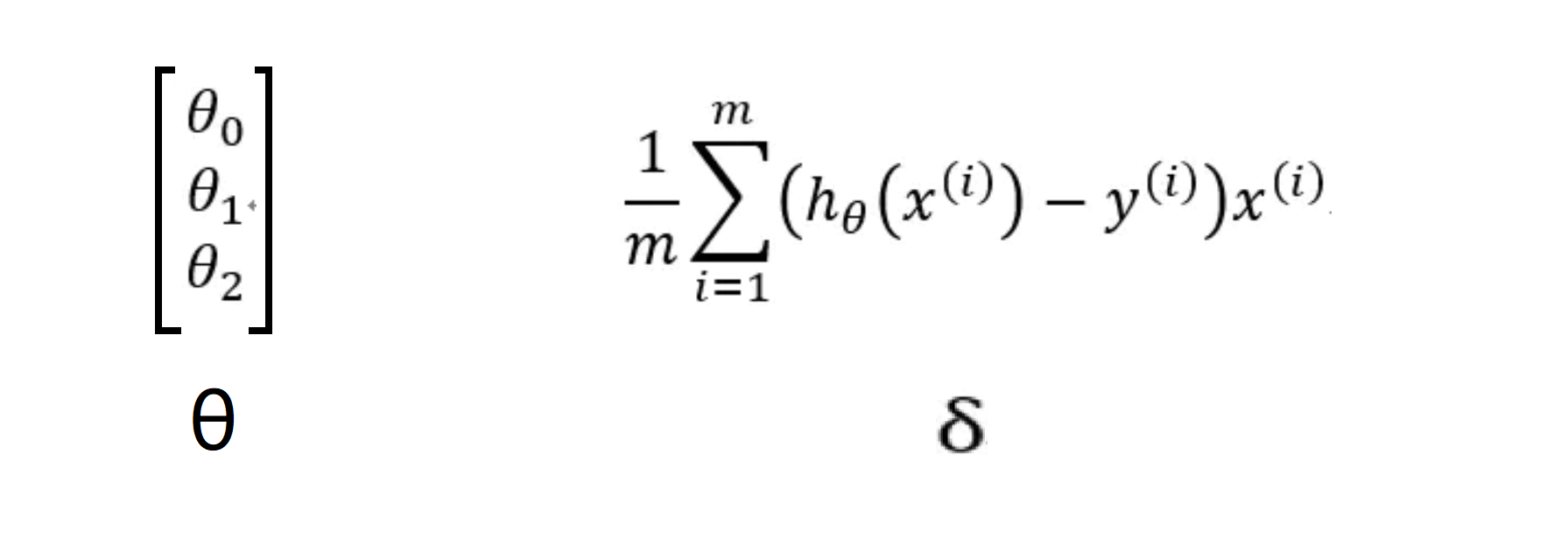
对于 δ, x(i)为 n+1 维向量,前面为常数,所以 δ 也为n+1 维向量。
我们改写 δ 为矩阵:
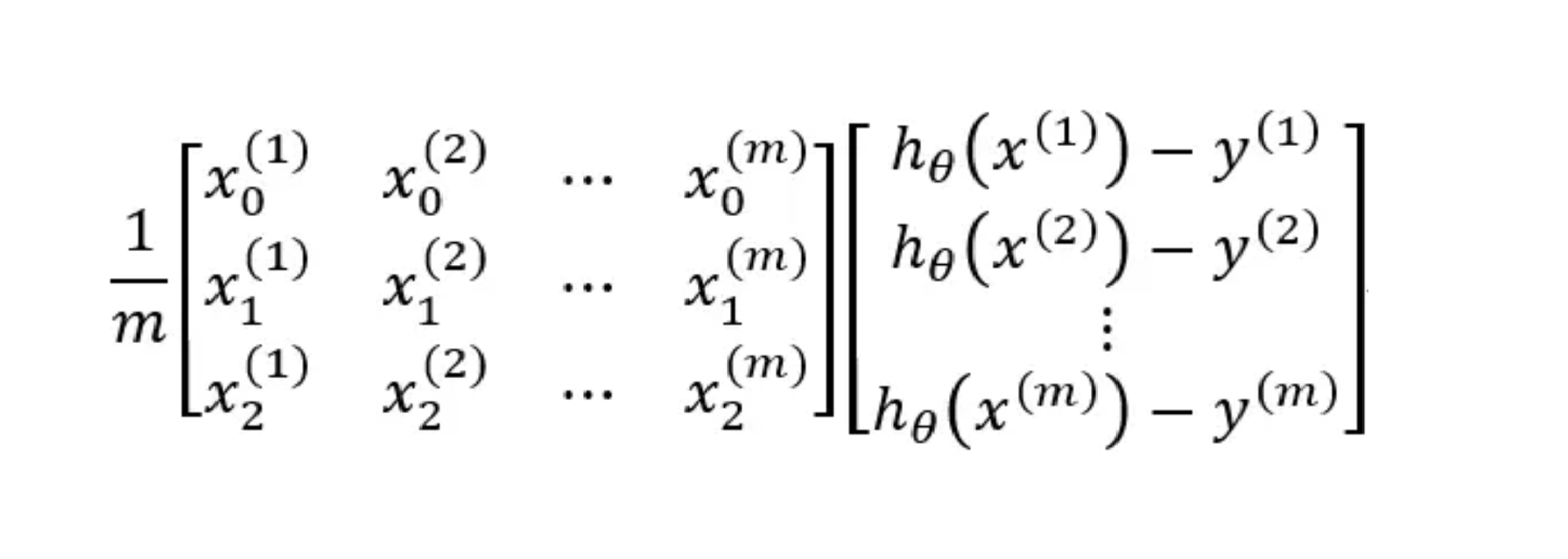
其中左边的矩阵就是X的矩阵的转置,而右边的矩阵可通过h(x)的向量减去y得到,所以我们得到的最终计算的过程应为:
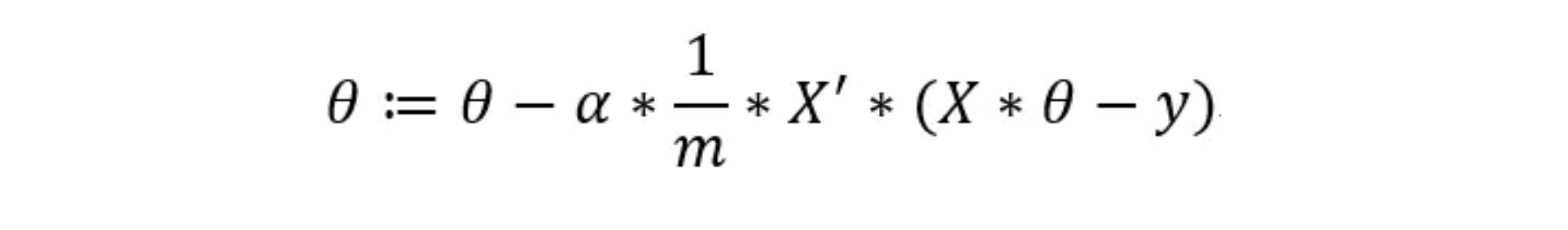
这样就可以用代码一步求解了。
结语
通过这篇BLOG,相信你已经初步掌握了参数向量化这个优化技巧,接下来我们还会一同学习更多更厉害的优化技巧。最后希望你喜欢这篇BLOG!
dalao太强辣ORZ
您更加强吧QwQ