在之前的BLOG中,我们已经初步掌握了矩阵的定义和一些简单的运算,这篇BLOG,就让我们继续看看矩阵中的一些进阶操作吧!
矩阵算术运算
矩阵的算术运算
首先是对于两个矩阵 A 和 C,如果想要得到这两个元素的积,前面提到过,只要A * C就好了:

同理对于除法加法减法也是一样的,这里就不赘述了。
矩阵元素的算术运算
而对于两个大小相同的矩阵 A 和 B,如果我想要对应位置的元素相乘,就要使用到A .* B:

同样地,如果想要 A 中的每个元素乘以 c ,我们就可以用A .* c,如果想要 A 中的每个元素除于 d ,我们也可以用A ./ d,如果想要 A 中的每个元素都变成自身的 e 次幂,我们也可以用A .^ e来实现:

对于矩阵或者向量 A ,我们还可以使用1 ./ A来让 A 中的所有元素变成自己的倒数:

类似的数学运算还有让 v 中所有元素对 e 取对数-log(v),所有元素 vi 变成 e^vi-exp(e):

还有对 v 中所有元素取绝对值的函数-abs(v),让 v 中所有元素变成自身的相反数的函数--v:

如果你想给你的向量 v 的每一个元素加上一个常数 c ,我们有两种方法,一种是v + c * ones(length(v), 1),另一种是直接v + c:

矩阵函数使用
接下来我们来看看一些常用的矩阵操作函数。
矩阵的转置和逆元
首先肯定是转置了,对于一个矩阵 A ,其转置就是A',记住转置的转置就是矩阵本身:

而pinv(A)可以求出 A 的逆(无逆时求出伪逆):
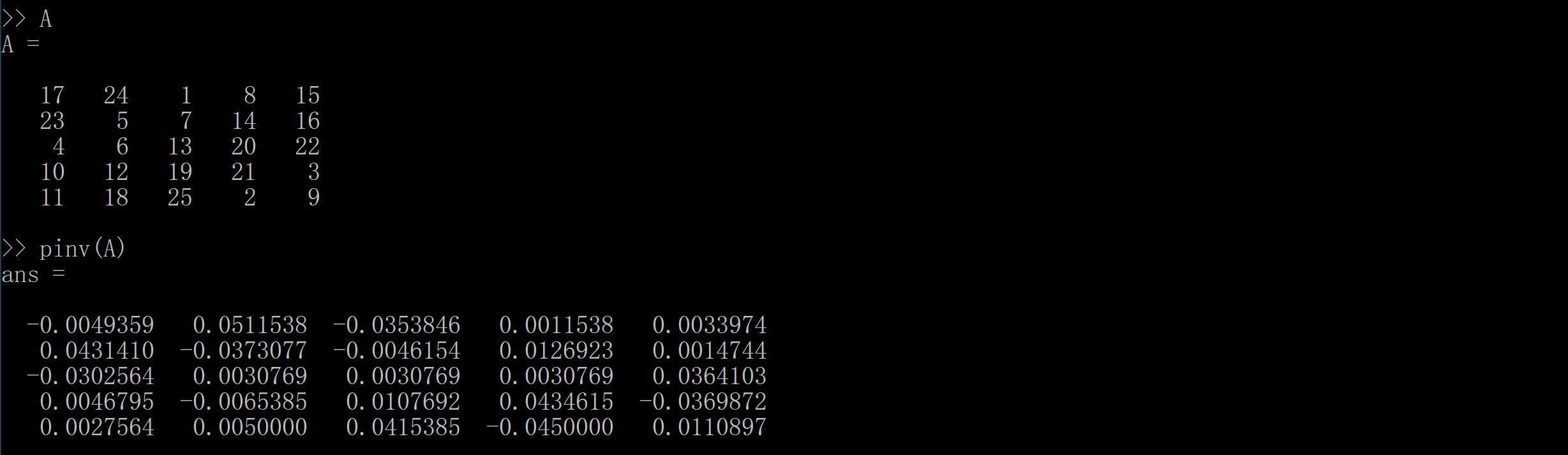
最值的计算
接下来我们来看看大名鼎鼎的max()函数。
首先对于一个行向量 a, max(a)可以直接得到 a 中的最大值,而[val, ind] = max(a)则不仅可以获得 a 中的最大值,还可以知道最大值出现在第几个元素:

而如果对于一个矩阵 B, max(B)就与max(B, [], 1)一样,返回的是一个行向量,记录的是每一列的最大值;而max(B, [], 2)返回的则是一个列向量,记录的是每一行的最大值:

所以如果要统计一个矩阵 B 的最大值,我们通常有两种办法,一种是直接max(max(B)),另一种是通过之前提到过的将所有元素变成一个列向量的max(B(:))的方式:

我们还可以对于两个大小相同的矩阵 A 和 B,max(A, B)输出的是每个对应位置上 A 和 B 中元素的最大值:

元素的寻找
首先,对于一个行向量 a ,如果我想知道每个元素是否小于 3 ,我可以直接使用a < 3,返回的也是一个向量,反应的是对应 a 位置是否小于 3 ,是则为 1 ,不是则为 0 :

我也可以运用上面的结果,结合find(条件)函数找到满足条件的元素的位置,比如find(a < 3)可以找到所有小于 3 的元素的下标:

而对于矩阵 A 而言,find(条件)同样适用,比如[r, c] = find(A >= 7)可以找到 A 中所有大于等于 7 的元素的坐标:

在上面这个例子中,坐标为(1,1)(3,2)(2,3)的元素均满足大于等于 7 的条件。
累乘和累加
对于一个行向量 a, 我们可以通过sum(a)来得到 a 中所有元素的累加和,通过prod(a)类得到 a 中所有元素的累乘:

而对于一个矩阵 A,我们可以通过sum(A, 1)来得到每一列的累加和,sum(A, 2)来得到每一行的累加和,prod也是同理的:

向下取整和向上取整
对于一个矩阵或者向量 a ,我们可以通过floor(a)来让所有元素向下取整,也可以通过ceil(a)来让所有元素向上取整:

奇幻矩阵
下面我们要见到的,是一种叫做奇幻矩阵的特殊方阵,对于 n 阶的奇幻矩阵,其每个元素都不重复且均在 1 - n^2 中,并且每一行每一列和两条对角线上的元素的和都是相同的,在Octave中,我们可以使用magic(n)来生成一个n阶的奇幻矩阵:

镜像翻转
我们如果想要只保留一个 n 维方阵 A 的主对角线上的元素,我们只要A .* eye(n)就可以了:
那如果我要反对角线上的元素呢?很容易想到,只要 A 乘以一个单位矩阵沿着竖直的中轴线翻转的矩阵就可以了。那如何实现这样镜像翻转呢?其实对于矩阵 B ,flipud(B)得到的就是 B 沿着竖直的中轴线翻转所得到的矩阵,所以操作也就很简单了:
