这次我们要介绍一个很高大上的东西FFT！，看完这篇博客，希望你能学会FFT，让多项式乘法成为你眼中的一道水题！:smile: :smile:

多项式乘法

顾名思义，就是两个多项式相乘。而我们要求的，就是相乘后各个项的系数，例如：
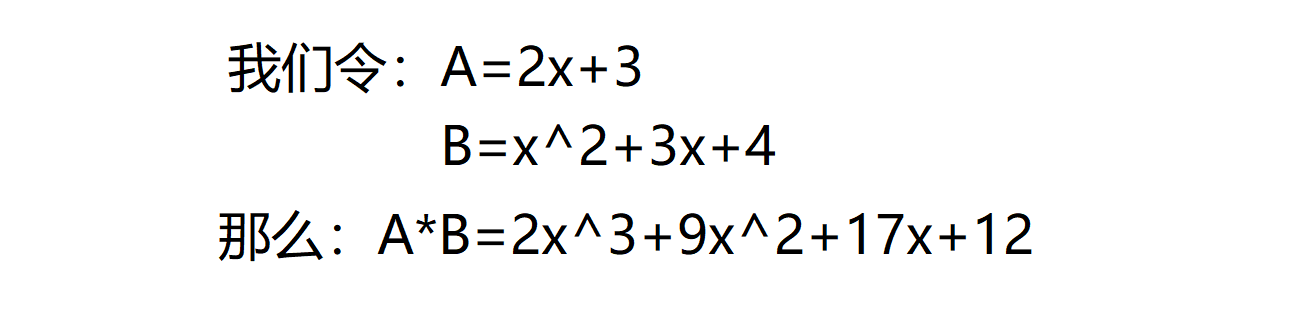
fft1.png
很显然我们可以通过手动暴力模拟来计算后各个项的系数，但复杂度却已经达到了O（n^2）,在n到达10^5级别时就已经完美TLE了。

这就引导我们要在O（nlogn）的复杂度下求解多项式乘法，所以这里就要隆重介绍今天的主角——FFT。

DFT和FFT的基本概念

简单来说，傅里叶变换，在OI中就只有一个用途——加速多项式乘法，而其方法简单来说就是：
构造多项式——FFT——点值乘法——IFFT

DFT（Discrete Fourier Transform）

即离散傅里叶变换，在这里的运用主要就是多项式的系数向量转换为点值表示的过程。

FFT（Fast Fourier Transformation）

即快速傅里叶变换，是离散傅里叶变换的加速算法，可以在 O(nlogn) 的复杂度下完成DFT，同理也可以在 O(nlogn) 的复杂度下完成逆DFT。

基本的一些数学知识

多项式表达法

次数表达法

先定义一个最高次数为n-1（次数界为n）的多项式：

A（x）=a0+a1*x+a2*x^2+……+an-1*x^n-1

上面这个就是次数表达法了，也是我们平常最常见的表示方法。而这个多项式的系数可以表示为一个由系数组成的向量 a=（a0，a1，a2，……，an-1）

点值表达法

什么是点值表示法呢？我们可以尝试吧我们的多项式理解为一个函数，然后用函数上的点来表示这个多项式。（两点确定一条直线，三点确定一个二次函数，……，n个点确定一个n-1次函数）

次数为n的多项式的点值表示法就是一个n个点对组成的集合：
{(x0,y0),(x1,y1),(x2,y2),……,(xn-1,yn-1)}

那么点值表示法由什么用呢？它可以在O(n)的时间复杂度下进行多项式乘法？怎么操作呢？
我们设A：
{(x0,Ay0),(x1,Ay1),(x2,Ay2),……,(xn-1,Ayn-1)}
我们设B：
{(x0,By0),(x1,By1),(x2,By2),……,(xn-1,Byn-1)}
那么c=A*B=:

{(x0,Ay0*By0),(x1,Ay1*By1),(x2,Ay2*By2),……,(xn-1,Ayn-1*Byn-1)}

这在FFT中起到了很大的作用。

单位复数根

fft2.png
在上面说讲到的n次单位复数根——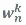wkn.png的含义是wn^k，这是什么意思呢？
通过计算我们会发现wn^0乘以wn，就会变成wn^1；同理，wn^1乘以wn，就会变成wn^2……
也就是说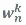，wkn.png为一个公比为wn的n项等比数列。

fft3.png
fft4.png

如下图，下图为四次单位复数根：
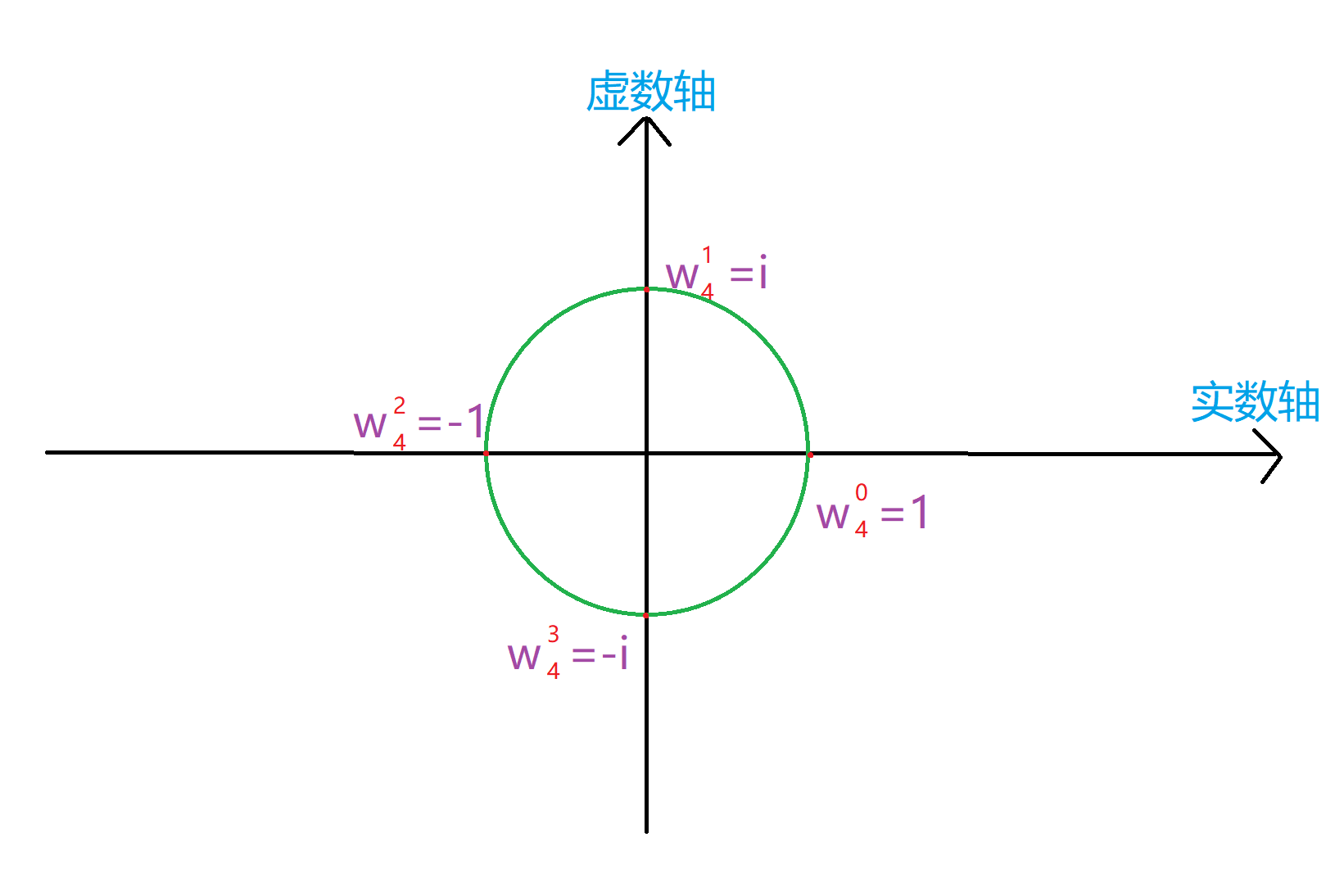
fft5.png

是不是很简单易懂啊QwQ

一些单位复数根的引理

消去引理

fft6.png

折半引理

fftf7.png

求和引理

fft8.png

DFT离散傅里叶变换

哈哈，终于到今天的的重头戏之一——DFT了!
我们希望次数为n的多项式：
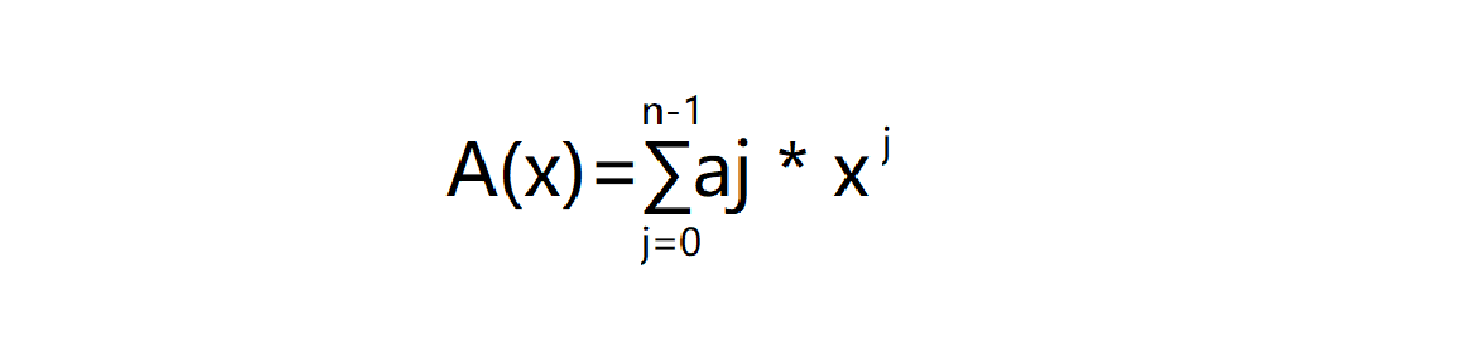
fft9.png
求出在：wn^0,wn^1,wn^2,……,wn^(n-1)[即n个n次单位复数根]的值，即将次数表达法转换为点值表达法。

使用插值法，时间复杂度达到了O(n^2)。这种比较落后的方法就是DFT（离散傅里叶变换）。

FFT快速傅里叶变换

利用单位复数根的特殊性质（上面介绍的三种引理），我们可以在O(nlogn)的时间内计算出 A（x） 进行傅里叶变换后的点集。

说到从O(n^2)到O(nlogn)的优化，你一定很自然的想到分治算法，没错FFT正是分治优化过后的DFT。

我们采用分治的策略，先分离出A（x）中以奇数下标和偶数下标为系数的数，形成两个新的次数界为n/2的多项式A0（x）和A1（x）；
A0(x)=a0+a2*x+a4*x^2+……+a(n-2)*x^(n/2-1)
A1(x)=a1+a3*x+a5*x^2+……+a(n-1)*x^(n/2-1)

那么我们可以很容易得到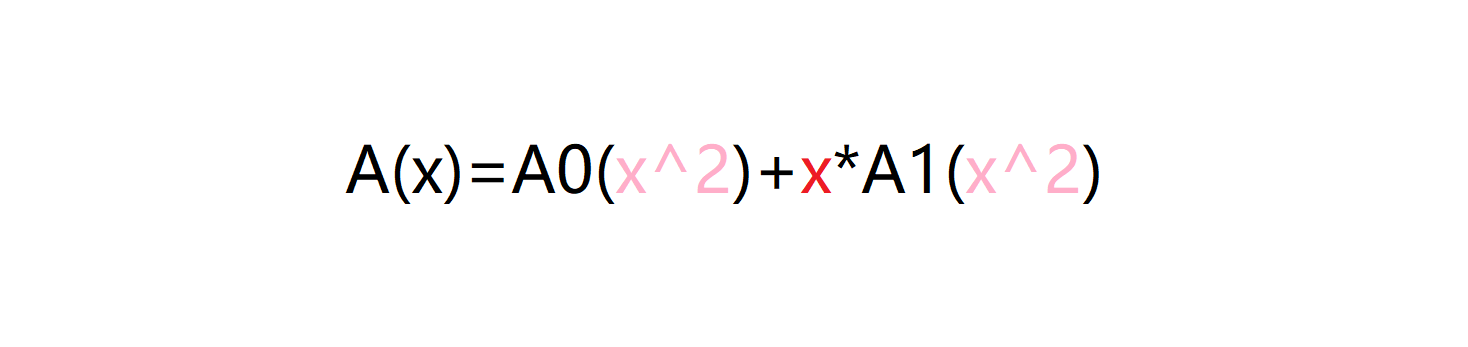：fft10.png
为什么是这个？你把上式展开，就发现会等于原式A(x)。

所以求A（x）在wn^0,wn^1,wn^2,……,wn^(n-1)处的值就转换为：
求A0（x），A1（x）在(wn^0)^2,(wn^1)^2,(wn^2)^2,……，(wn^(n-1))^2 处的值。

根据折半引理，上式并不是由n个不同值组成，而是仅仅由n/2个n/2次单位复数根组成，每个根刚好出现两次。

所以我们可以继续向A0(x)和A1(x)递归求出他们的值，每次规模为原来的一半，这样我们就把一个n个元素的DFT，变为两个n/2个元素的DFT，再变为四个n/4个元素的DFT………………【边界：w1^0=1,所以w1^0*a=a】

下面我们举个栗子！

fft11.JPG

接着我们再对G(x)和H(x)也进行一样的操作跑一下FFT；这样递归下去，总的复杂度为O(n log n)。

IFFT快速傅里叶逆变换

我们FFT得到的是什么？是点值表示法，这时我想想得出具体的系数表示法，具体思路就是在单位复数根处插值。这里只要记住结论就好了：我们用wn^-1代替wn，并将解结果每个除以n，得到的就是逆DFT的结果，即所想要的系数表示法。

具体代码实现：

原理我们都明白了，那就直接上代码了：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring> 
#include<complex>//c++自带的复数库
#include<algorithm>
using namespace std;
double pi=acos(-1);

complex<double> a[410000],b[410000],c[410000];
int i,j,k,m,n,o,p,js,jl;

void fft(complex<double> *a,int n,int op)
{
    if(n==1)return; 
    complex<double> w(1,0),wn(cos(2*pi/n),sin(2*pi*op/n)),a1[n/2],a2[n/2];

    for(int i=0;i<n/2;i++)
    {
        a1[i]=a[2*i];
        a2[i]=a[2*i+1];
    }
    fft(a1,n/2,op);
    fft(a2,n/2,op);

    for(int i=0;i<n/2;i++)
    {
        a[i]=a1[i]+w*a2[i];
        a[i+n/2]=a1[i]-w*a2[i];
        w=w*wn;
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;i++)scanf("%lf",&a[i]);
    for(int i=0;i<=m;i++)scanf("%lf",&b[i]);
    m=m+n;n=1;
    while(n<=m)n=n*2;

    fft(a,n,1);fft(b,n,1);
    for(int i=0;i<=n;i++)c[i]=a[i]*b[i];
    fft(c,n,-1);
    for(int i=0;i<=m;i++)printf("%d ",int(c[i].real()/n+0.5));
    return 0;
}

经典例题

【luogu 1919】A*B Problem升级版

题目描述
给出两个n位10进制整数x和y，你需要计算xy。
输入输出格式
输入格式：
第一行一个正整数n。 第二行描述一个位数为n的正整数x。 第三行描述一个位数为n的正整数y。
输出格式：
输出一行，即xy的结果。（注意判断前导0）
输入输出样例
输入样例#1：
1
3
4
输出样例#1：
12
说明
数据范围：
n<=60000
来源：bzoj2179

很明显高精度乘法和我们多项式乘法的运算有着异曲同工之妙，如果跑DFT就和高精度乘法一模一样，但会超时。所以这里我们要用FFT进行加速，最后再加一些对进位和去首位0的操作就能AC了，附上代码：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring> 
#include<complex>//
#include<algorithm>
using namespace std;
double pi=acos(-1);

complex<double> a[410000],b[410000],c[410000];

int ans[410000];
char sa[410000],sb[410000];
int i,j,k,m,n,o,p,js,jl;

void fft(complex<double> *a,int n,int op)
{
    if(n==1)return; 
    complex<double> w(1,0),wn(cos(2*pi/n),sin(2*pi*op/n)),a1[n/2],a2[n/2];

    for(int i=0;i<n/2;i++)
    {
        a1[i]=a[2*i];
        a2[i]=a[2*i+1];
    }
    fft(a1,n/2,op);
    fft(a2,n/2,op);

    for(int i=0;i<n/2;i++)
    {
        a[i]=a1[i]+w*a2[i];
        a[i+n/2]=a1[i]-w*a2[i];
        w=w*wn;
    }
}
int main()
{
    scanf("%d",&n);
    scanf("%s",sa+1);scanf("%s",sb+1);
    for(int i=0;i<n;i++)a[i]=double(sa[n-i]-'0'); 
    for(int i=0;i<n;i++)b[i]=double(sb[n-i]-'0'); 
    n--;
    m=2*n;n=1;
    while(n<=m)n=n*2;

    fft(a,n,1);fft(b,n,1);
    for(int i=0;i<=n;i++)c[i]=a[i]*b[i];
    fft(c,n,-1);
    for(int i=0;i<=m;i++)ans[i]=int(c[i].real()/n+0.5);
    for(int i=1;i<=m;i++)
    {
        ans[i]=ans[i]+ans[i-1]/10;
        ans[i-1]=ans[i-1]%10;
    }
    int bb=1;
    for(int i=m;i>=0;i--)
    {
        if(ans[i]>0)bb=0;
        if(bb==0)printf("%d",ans[i]);
    }
    return 0;
}

结语

通过这篇BLOG，你肯定已经学会如何实现FFT了！快去刷刷题巩固一下吧！希望你喜欢这篇BLOG！

Last modification：June 18th, 2019 at 07:08 pm
© 允许规范转载
If you think my article is useful to you, please feel free to appreciate