在之前的BLOG里，我们介绍了通过梯度下降法来解决回归问题。在这篇BLOG中，就让我们学习一种新的解析方法——正规方程法吧。

正规方程法

到之前的BLOG中，我们一直在使用梯度下降法来解决线性回归问题，也就是使用的迭代算法，经过很多步迭代来计算最值所对应的 θ 。但正规方程法(Normal Equation) 提供了一种求 θ 的解析解法，也就是可以一次求解最优时 θ 的值。

在讲正规方程法之前，我们再讲讲另一种解析解法——方程法。先举一个例子来解释这个问题，我们假设，有一个非常简单的代价函数 J(θ) 其是关于参数 θ 的二次函数：

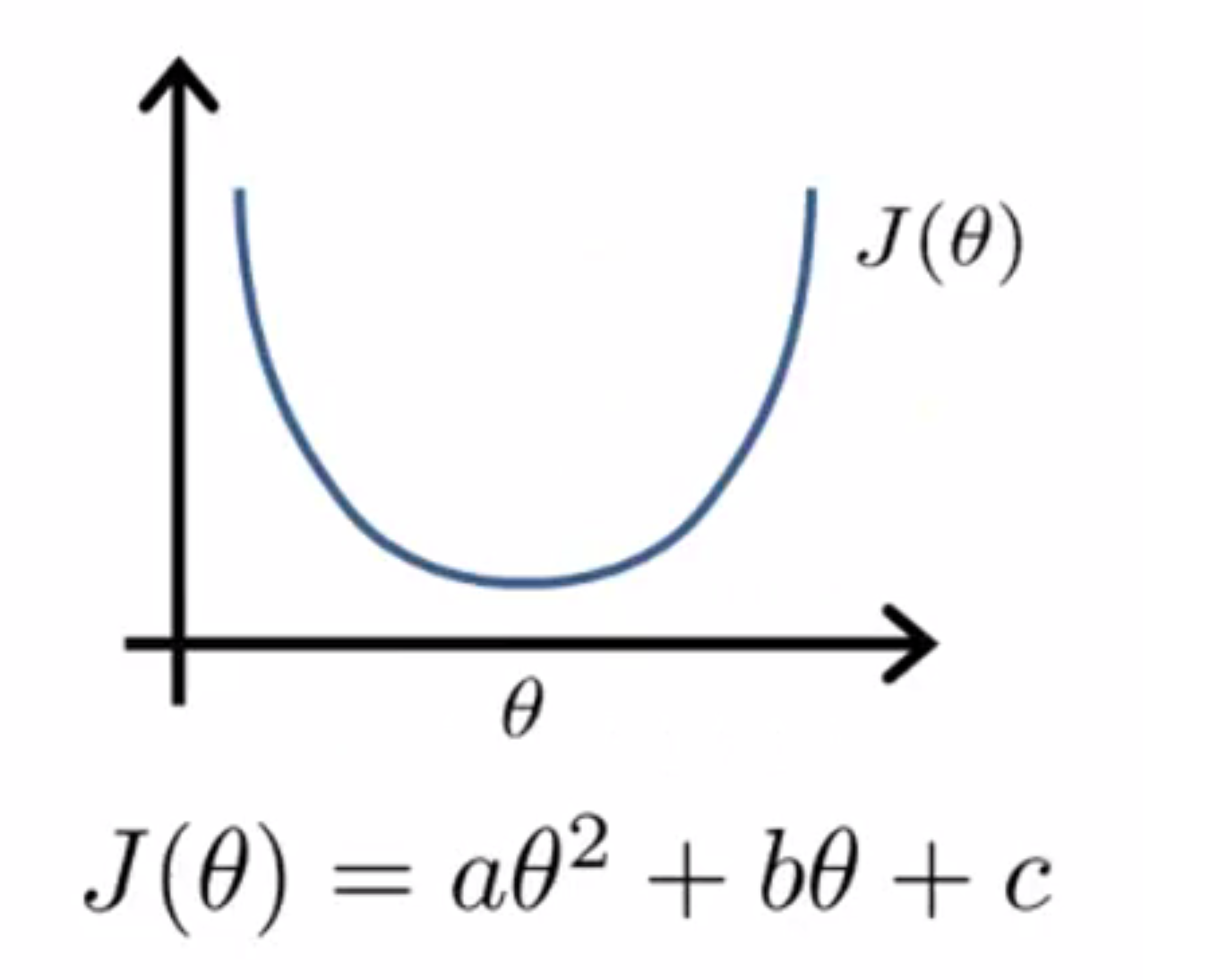
那么如何求解一个函数的最低点呢?学过数学分析/高等数学的同学就知道，要求解一个函数的最值，其实就是要去找那些导数值等于 0 或者导数值不存在的点。当 θ 只是一个实数的时候，这时很容易实现的，只需要解一个方程就可以了；但如果 θ 不是一个实数，而是一个 n+1 维的参数向量的时候我们又该怎么办呢？此时代价函数 J 是向量 θ 的函数，也就是 θ0 到 θn 的函数，大概是这样：

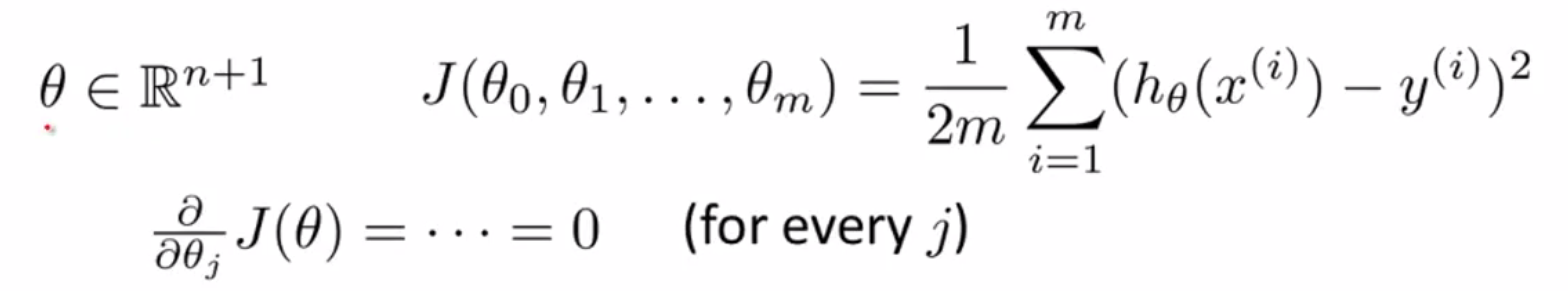
我们其实要对每个参数 θ 求 J 的偏导数，然后求出满足所有偏导数都不存在或等于 0 的解，最值就出现在里面，但是这时非常麻烦的。

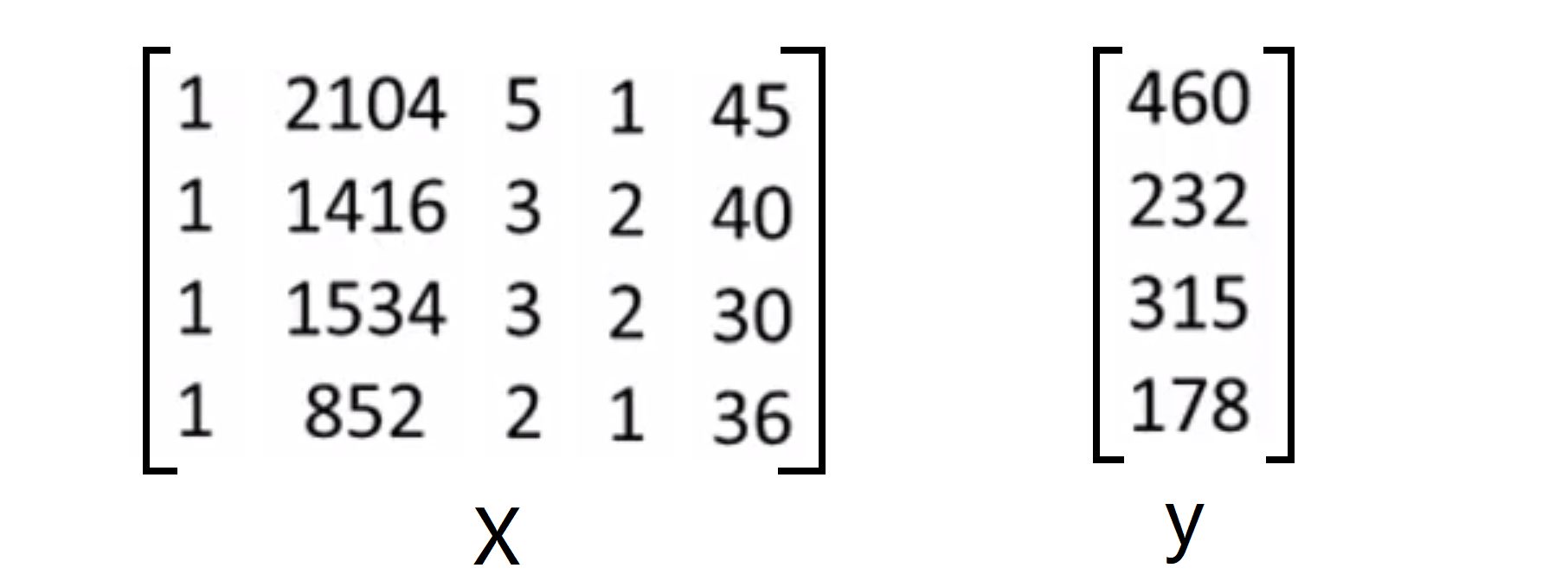
但我们我们接下来要讲的正规方程法不需要这些数学分析/高等代数的知识，我们只需要一些线性代数的知识就可以了。具体怎么操作，让我们来再次通过卖房子的例子来说明吧。假如说我有 m = 4 的训练样本：

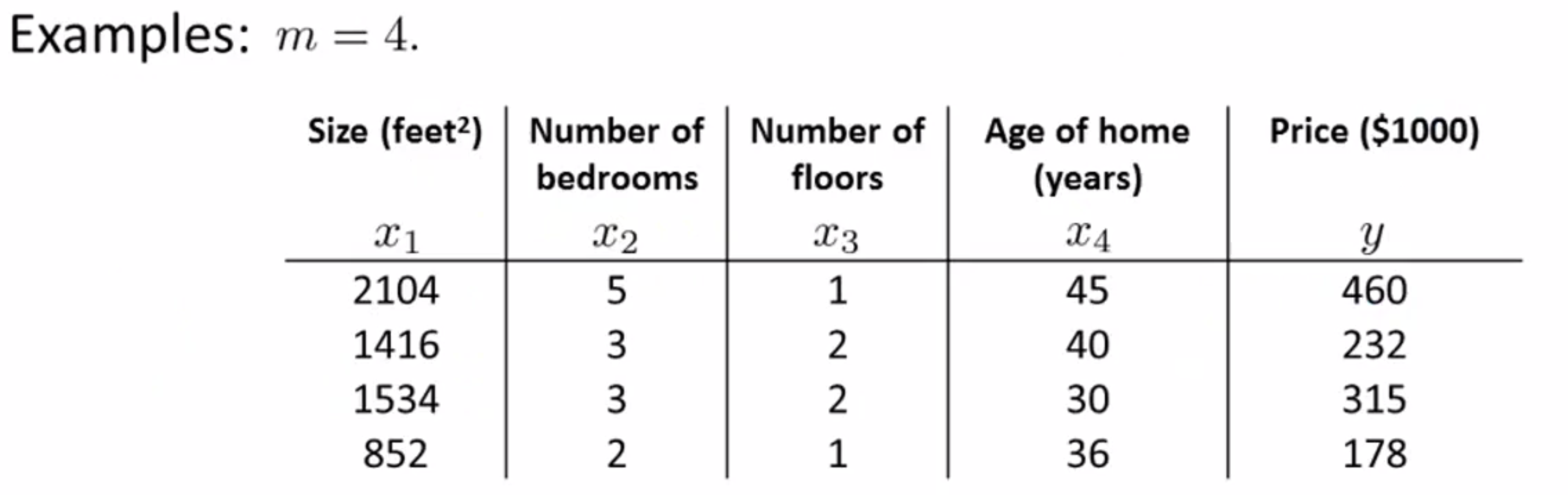
我们首先要做的就是在训练集中加上一列对应额外特征变量的x，其值恒为 1：

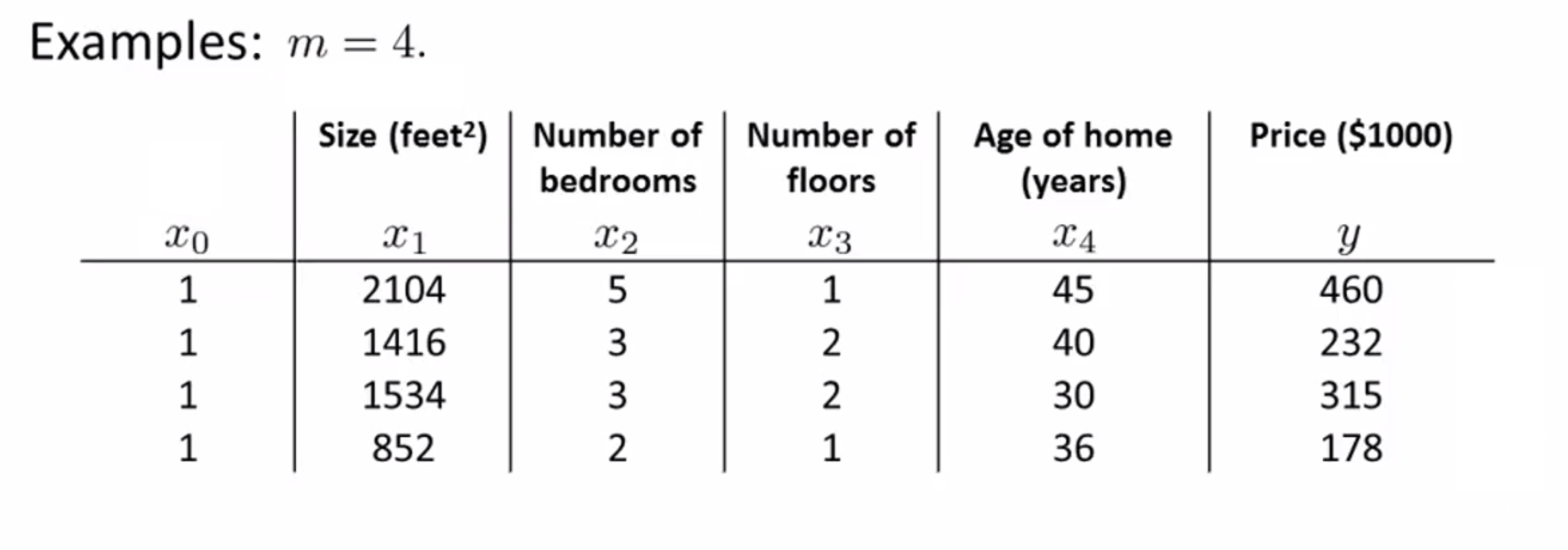
下来我们要构建一个矩阵 X 这个矩阵基本包含了训练样本的所有特征变量，这个矩阵基本包含了训练样本的所有特征变量，也即是说我们要将表格中的所有特征值放到一个矩阵当中，所以 X 会是一个 m*(n+1) 维矩阵：

接下来我们还要构造一个向量y，我们要将要预测的值建一个向量，并且称之为向量 y ，所以 y 会是一个 m 维向量：

接着我们来分析一下，我们最后求出的回归方程应该是 h0(x) = 00 + 01 * x1 + 02 * x2 + 03 * x3 + 04 * x4,我们一样地，构造一个向量 p 为 p = [00, 01, 02, 03, 04]，那如果我们的数据是完全在我们的回归直线上，那就应该有 X * p = y，即p = X^T * y。

但实际上，我们会遇到两个问题，第一数据大多情况下是均匀地分布在我们的直线两边的，所以我们可以用线性代数中的最小二乘法进行逼近；第二，只有方阵才有逆矩阵，而大多数情况下我们的 X 都是普通的矩阵，所以我们要用到SVQ里面用到过的伪逆的概念。

思路就是上面说的那样，具体的过程我就不进行推到了，其实最优情况下的向量 0 就是满足下面一个式子：

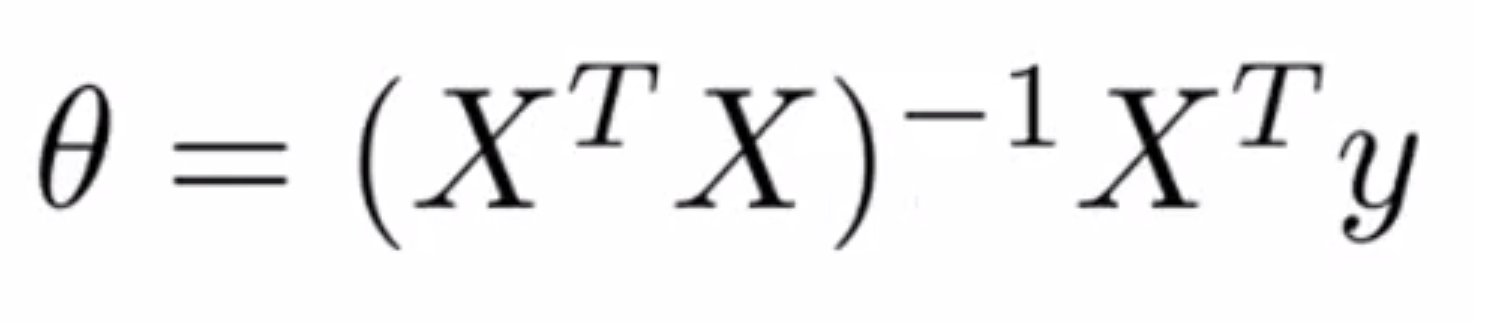
其中(X^TX)^-1代表X^TX的逆矩阵。再Octave中，这可以写成很简洁的一行代码pinv(x' * x) * x' * y。我没有去证明这个式子，因为证明过程可以在线性代数的树上找到，但你可以相信这个式子会给出最优的 θ 值。

最后我们来谈一谈什么时候可以使用这个正规方程法，其实最重要的就是这个特征值的数目n的大小。因为我们要计算(X^T*X)^-1，这大概是个O(n^3)的工作，所以当n≥10000时，实际上花费的时间可能就不如梯度下降法了。但相反地，在 n 不太大的时候，正规方程法还是一种很不错的算法。

X^T*X的可逆性

可能有的同学会好奇，θ = inv(X'X )*X'y ，那对于矩阵X'X的结果是不可逆的情况咋办呢? 确实如果你懂一点线性代数的知识 ，有的有些矩阵可逆，而有些矩阵不可逆。其实X'X的不可逆的问题很少发生，在Octave里如果你用pinv来实现逆矩阵的计算，就算该矩阵不可逆，你也会得到一个正常的解，因为这时计算机帮你找到了一个类似于逆矩阵的矩阵，此时你的不可逆矩阵乘以这个矩阵是最接近单位矩阵的。

其实在Octave里，有两个函数可以求解矩阵的逆，一个被称为pinv()另一个是inv()，这两者之间的差异是些许计算过程上的，前者是所谓的伪逆，后者被称为严格的逆，使用pinv() 函数计算出比较正常的解，便矩阵X'X是不可逆的。

尽管如此，我们还是要尽量避免X'X结果是不可逆的情况的出现。如果矩阵X'X结果是不可逆的，通常有两种最常见的原因：

第一个原因是可能出现了多余的特征值，它和其他特征值始终保持线性关系。例如在预测住房价格时，如果x1是以英尺为尺寸规格计算的房子，x2是以平方米为尺寸规格计算的房子，同时我们找到1米恒等于3.28英尺，那 x1 就恒等于 x2 的 3.28平方倍，即它们是线性相关的，所以此时 X'X 就会不可逆了。

第二个原因是可能在你的特征值太大了，这也可能会导致矩阵X'X的结果是不可逆的。具体地说，在训练样本数 m 小于或等于特征数 n 的时候，你的矩阵 X'X 就很可能是不可逆的了，这时你就要填充更多的数据或者重新审视你特征值的选取，是否有必要选取这么多之类的。

其实不可逆的情况在实际的操作中还是少之又少的，再加上Octave能够自动处理，所以只要知道大概的解决方案就可以了，不必倾注太多时间。

代码实现

思路在上面已经写的比较清楚了，下面我用Cpp进行了实现，供大家学习，其中求逆矩阵用了高斯消元法，不了解的同学可以点击这里进行学习：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
const double EPS = 1e-6;
double cpu[1100][2200];
double temp[1100][2200];
double x[1100][2200], y[1100];
double a[1100][2200],ans[2200];
const double Alpha = 3 * 1e-3;
void read() {
    printf("请输入样本大小m:\n");
    scanf("%d", &m);

    printf("请输入特征值的个数n:\n");
    scanf("%d", &n);

    for(int i = 1; i <= m; i++) x[i][1] = 1;
    n++;

    printf("请依次输入m个特征值xi和结果y:\n");
    for(int i = 1; i <= m ; i++) { 
        for(int j = 2; j <= n; j++) {
            scanf("%lf", &x[i][j]);
        }
        scanf("%lf", &y[i]);
    }
    return;
}

void gauss() {
    double multi;
    for(int i = 1; i <= n; i++) {//从左到右枚举第i列(即枚举主元列)

        if(fabs(a[i][i]) < EPS) {
            printf("Error!\n");
            exit(0);
        }

        multi = a[i][i];

        for(int j = i; j <= 2 * n; j++) a[i][j] /= multi;

        for(int j = 1; j <= n; j++) {
            if(j != i) {
                if(a[j][i] == 0)continue;
                else multi= a[j][i] / a[i][i];
                for(int k = i; k <= 2 * n; k++) {
                    a[j][k] -= a[i][k] * multi;
                }
            }
        }
        //通过初等行变化(即减去第i行的某个倍数)，我们将除第i行的第i列都变成0；
    }
}

void work() {
    memset(ans, 0, sizeof(ans));
    memset(cpu, 0, sizeof(cpu));
    memset(a, 0, sizeof(a));
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            for(int k = 1; k <= m; k++) {
                a[i][j] += x[k][i] * x[k][j];
            }
        }
    }
    for(int i = 1; i <= n; i++) {
        a[i][i + n] = 1;
    }

    gauss();

    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            temp[i][j] = a[i][j + n];
        }
    }

    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            for(int k = 1; k <= n; k++) {
                cpu[i][j] += temp[i][k] * x[j][k];
            }
        }
    }

    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            ans[i] += cpu[i][j] * y[j];
        }
    }

    return ;
}

void write() {
    printf("拟合出的直线为：");
    printf("y = %0.1lf", ans[1]);
    for(int i = 2; i <= n; i++) {
        if(ans[i] >= 0)printf(" + %0.1f * x%d", ans[i], i);
        else printf(" - %0.1f * x%d", -ans[i], i);
    }
    printf("\n");
}
int main() {

    read();
    work();
    write();
    return 0;
}  

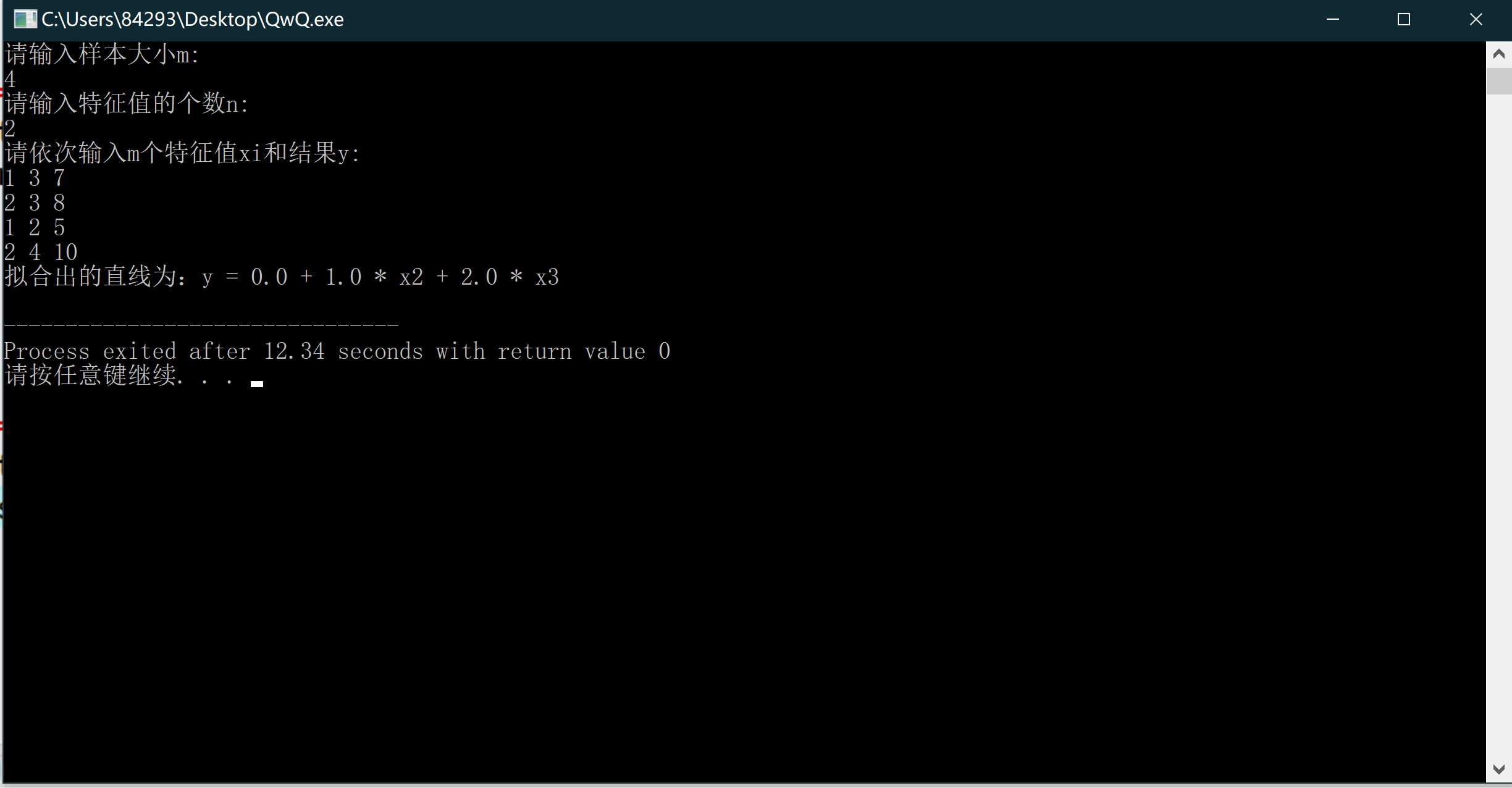
效果也是极为不错的：

结语

通过这篇BLOG，相信你已经掌握了机器学习的第二个算法正规方程法，之后我们还会继续学习更多更高效的算法。最后希望你喜欢这篇BLOG！