为了求解回归问题，我们一般采取梯度下降法来实现。但是往往因为一些优化还不到位，导致我们的梯度下降法用了很长时间才达到我们预期的结果，下面，就让我们一同康康梯度下降法的一些优化方法吧！

特征缩放

首先，让我们一同来看看一个叫做特征缩放 (feature scaling) 的常用方法。其主要思想就是 当我们在一个问题中涉及到多个特征时，如果你能确保这些特征都处在一个相近的范围，那梯度下降法就能更快地收敛。

我们举个具体的例子吧。假如我们有一个具有两个特征的问题，其中 x1 是房屋面积大小，它的取值在0到2000之间；x2 是卧室的数量，其取值范围在0到5之间。如果你画出代价函数 J(θ) 的轮廓图，那其应该大致如下图所示：

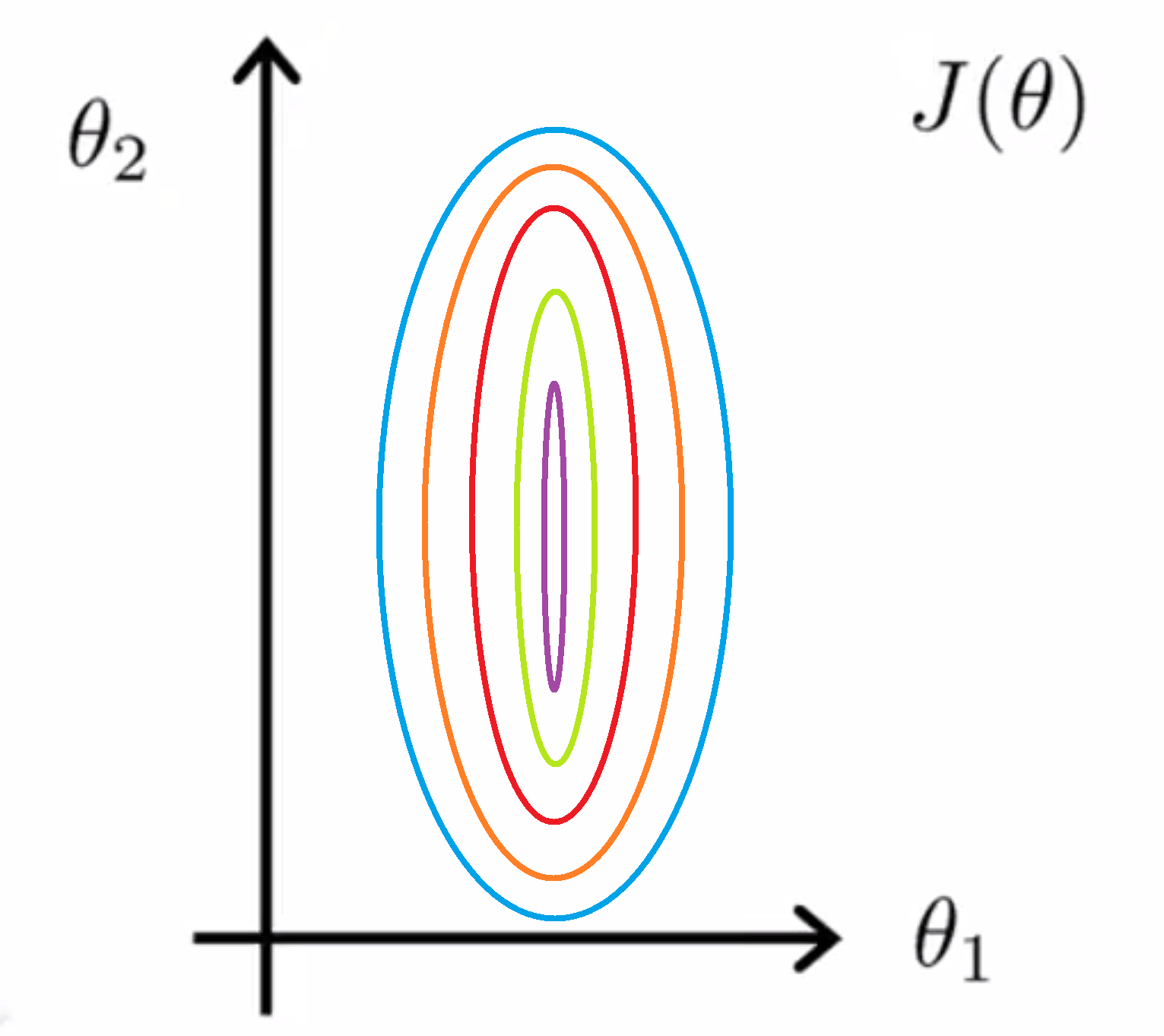
即如果 x1 的取值范围远远大于 x2 的取值范围的话 那么最终画出来的代价函数 J(θ) 的轮廓图就会呈现出这样一种非常偏斜并且椭圆的形状。

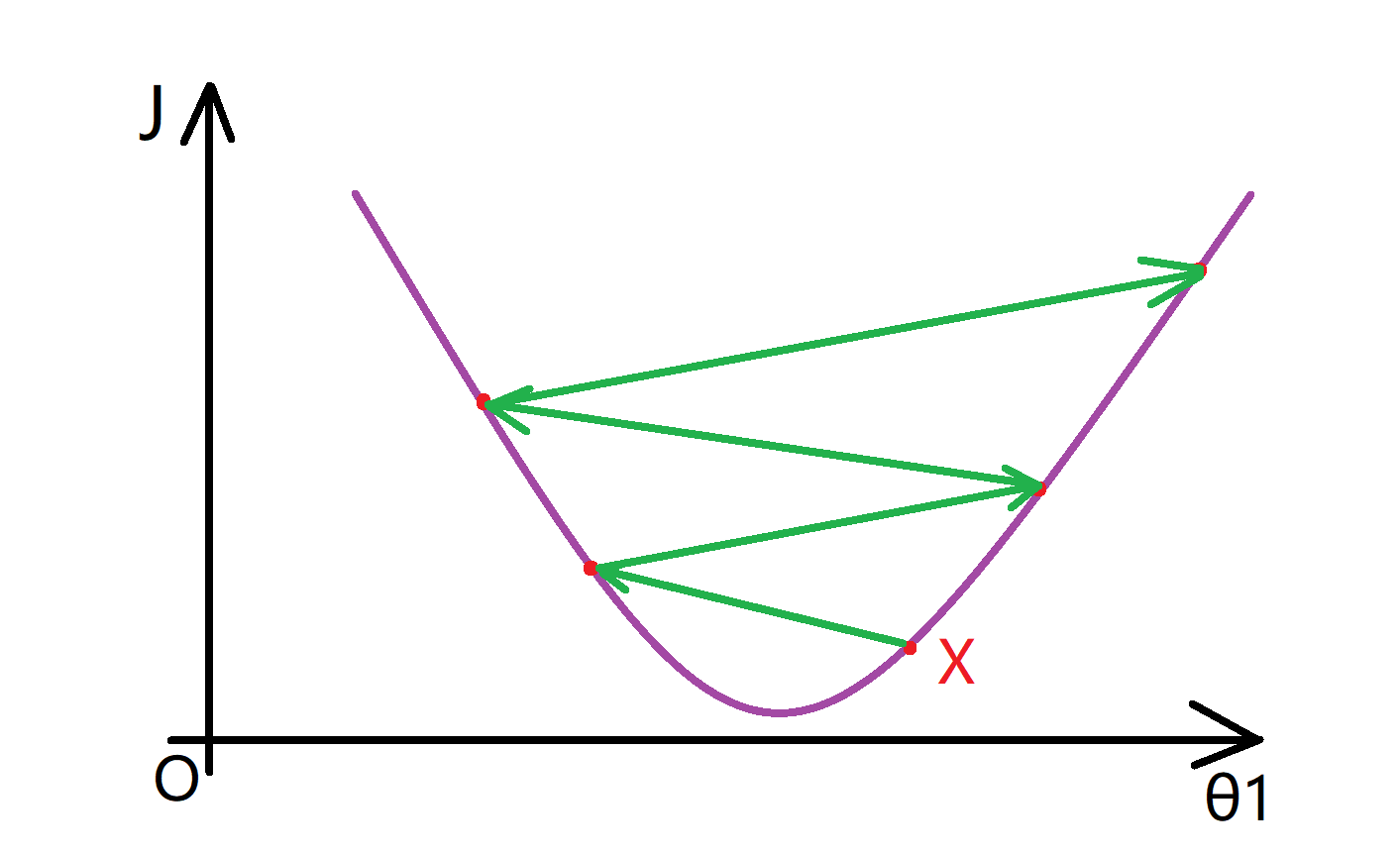
那这有什么问题吗？如果我们直接用这个代价函数来运行梯度下降的话，我们要得到梯度值就可能需要花很长一段时间，因为它可能可能会来回波动,然后会经过很长时间,最终才收敛到全局最小值:

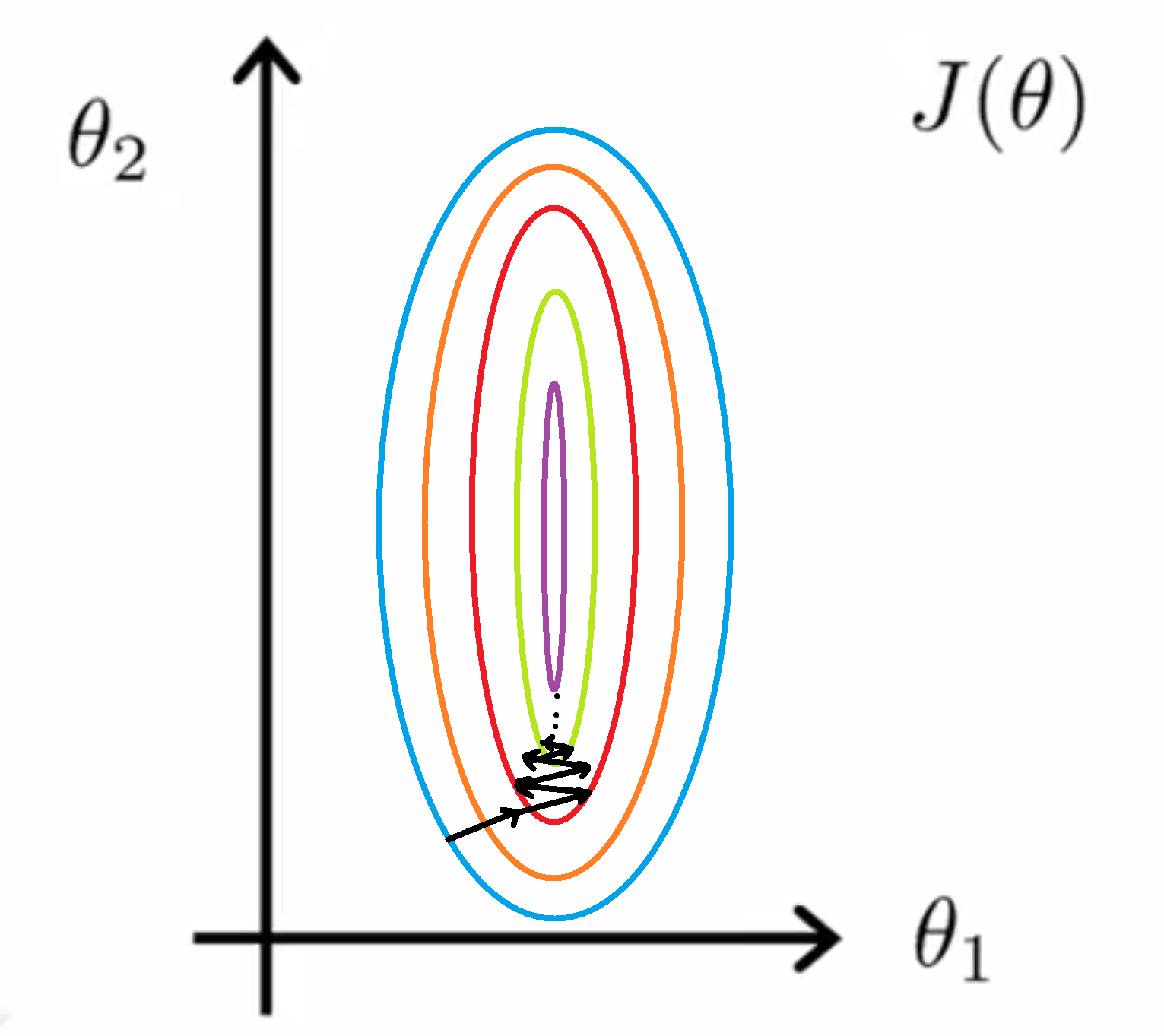
更夸张地，如果两个变量的比例再被放大一些的话，代价函数就会变得更细更长，那么可能情况会更糟糕，梯度下降的过程可能更加缓慢，我们也需要花更长的时间，反复来回振荡，最终才找到一条正确通往全局最小值的路。

在这样的情况下，一种有效的优化方法是进行特征缩放。具体来说，就是把每个除于它们的大致范围。比如在上面那个例子中，我们把特征值 x1 改写为 房子的面积大小 除以2000的话，并且把 x2 改写为 卧室的数量除以5。这样的话代价函数 J(θ) 的轮廓图的形状就会更加圆润:

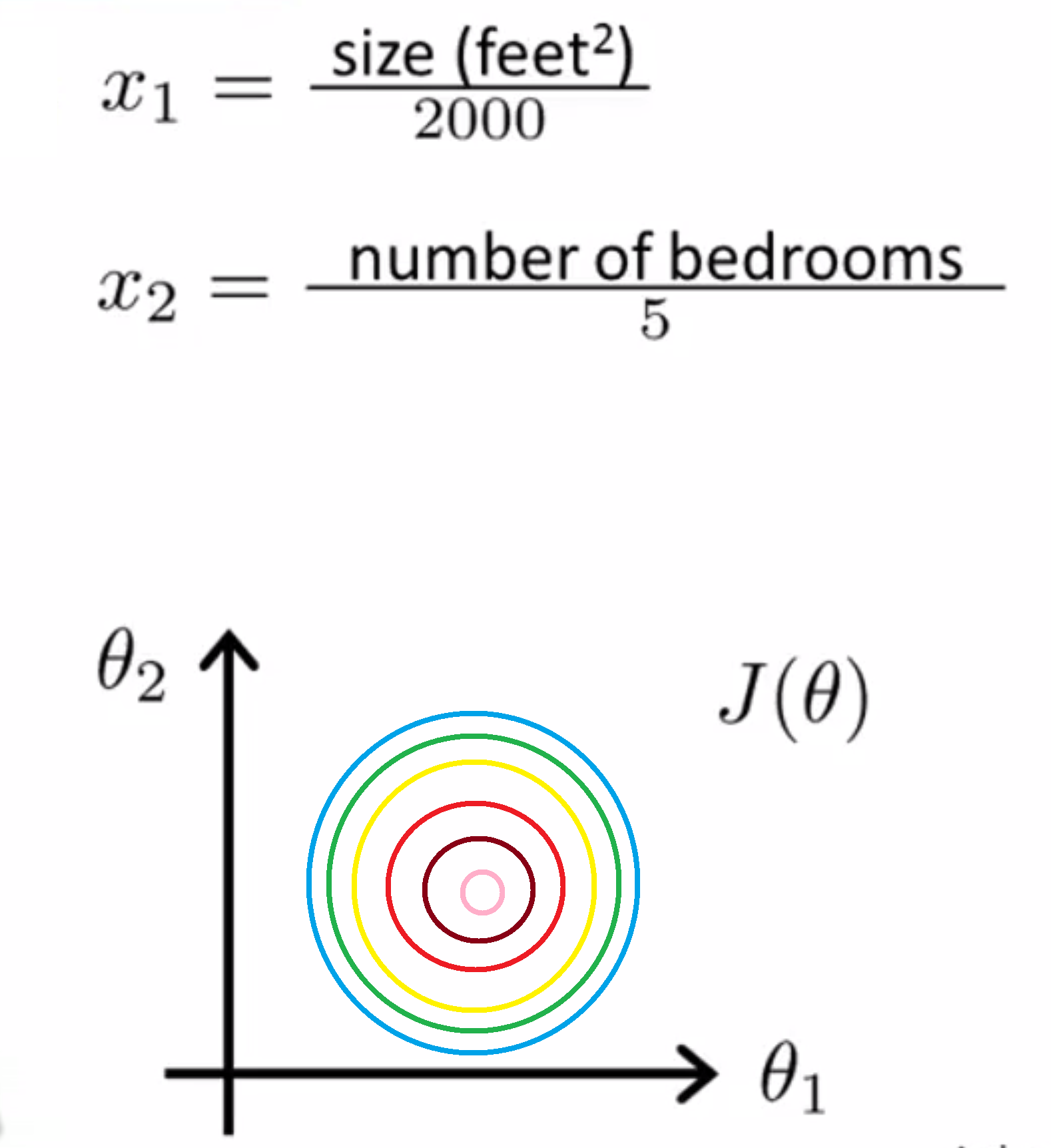
如果你用这样的代价函数来执行梯度下降的话，那么你可以从数学上来证明，这样的梯度下降算法就可以用更小的步数来到达我们的全局最小值。因此通过特征缩放，通过"消耗掉"这些值的范围，比如在这个例子中，我们最终得到的两个特征 x1 和 x2 都在0和1之间，这样我们得到的梯度下降算法就会更快地收敛。

更一般地，我们在使用特征缩放时，我们通常会将将特征的取值约束到 -1 到 +1 的范围内。而我们的的特征值 x0 是总是等于1，因此经是在这个范围内，就无需处理了，但对其他的特征，你可能需要通过除以不同的数，来让它们大致处于同一范围内。记住 -1 和 +1 这两个数字并不是太重要！不一定要限定的那么死。所以如果你有一个特征 x1 它的取值在0和3之间这没问题，如果你有另外一个特征 x2 取值在-2 到 +0.5之间，这也没什么关系，这些都非常接近 -1 到 +1的范围；但如果你有另一个特征x3 它的范围 在 -100 到 +100 之间，那么这个范围跟 -1 到 +1 就有很大不同了，所以这就是一个不那么好的特征，你需要进行放缩，类似地，如果你的特征在一个非常非常小的范围内，比如另外一个特征 x4 它的范围在 0.0001和+0.0001之间，那么这同样是一个比 -1 到 +1 小得多的范围，你也要进行缩放。

具体来说，我们一般可以这么考虑的，如果一个特征是在 -3 到 +3 的范围内，那么你应该认为这个范围是可以接受的。但如果这个范围大于了 -3 到 +3 的范围，我可能就要开始注意了；同样地如果它的取值 在-1/3 到+ 1/3 的话也是可以接受，或者是 0 到 1/3 或 -1/3 到0，这些都是典型的可接受范围。但如果特征的范围取得很小的话，比如像这里的 x4 你就要开始考虑进行特征缩放了。

所以总的来说，不用过于担心你的特征是否在完全相同的范围或区间内，只要它们的范围足够接近的话，梯度下降法就能够正常地工作。

均值归一化

除了简单的特征缩放，有时候我们也会进行一个被称为均值归一化(mean normalization)的工作。其具体流程就是，如果我们有一个特征值 xi 你就用 （xi - μi）/(x_max - x_min)来代替. 通过这样做，让我们的特征值都具有为0的平均值且范围变成了 1 。我们不需要把这一步应用到 x0中，因为 x0 总是等于1的，所以它不可能有等于 0 的平均值。

继续用之前的例子，假如我们有一个具有两个特征的问题，其中 x1 是房屋面积大小，它的取值在0到2000之间；x2 是卧室的数量，其取值范围在0到5之间。对于房子的大小取值介于0到2000，并且假如房子面积的平均值是等于1000的 那么你可以用这个公式，让训练集的所有 x1 = (x1 - 1000) / 2000 ；类似地如果平均一套房子有两间卧 那么你也可以类似地使用这个公式来归一化你的第二个特征 x2 = (x2 - 2) / 5 .在这两种情况下,你可以算出新的特征 x1 和 x2 这样它们的范围,它们都在在 0 和 1 之间：

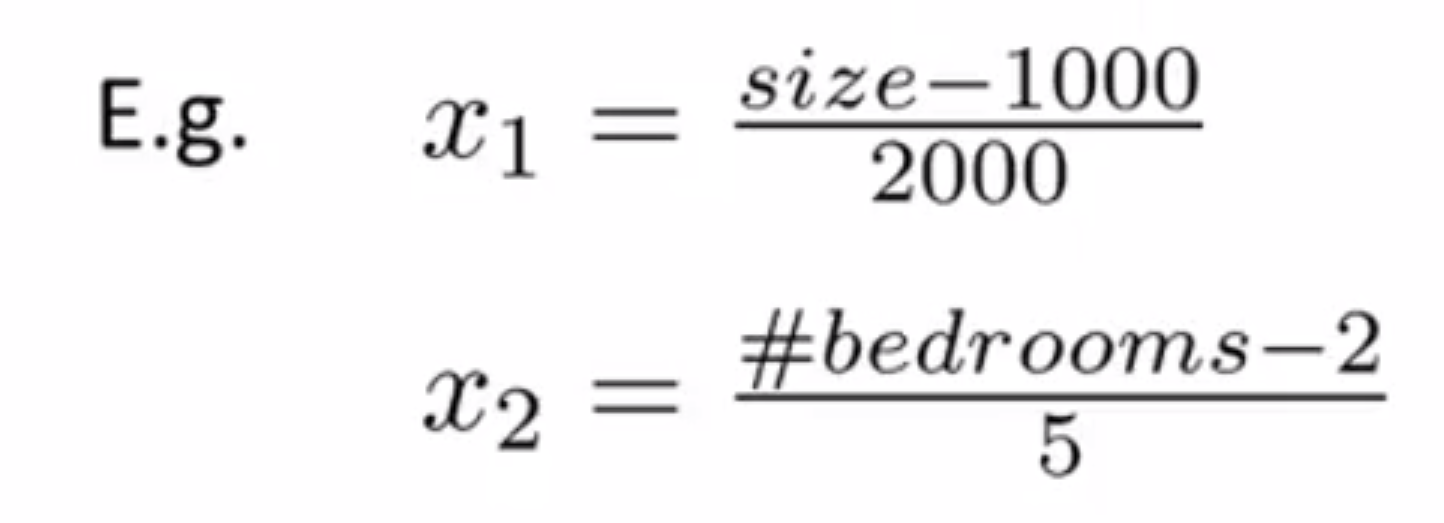
其实更一般的规律是，你可以用这样的公式，你可以用 (xi- μi) / Si 来替换原来的特征 xi。其中 μ1 的意思是在训练集中特征 xi 的平均值，而 Si 是 该特征值的范围，即是指最大值减去最小值。

其实在现实运用中，只要将特征转换为相近似的范围就都是可以的。特征缩放其实并不需要太精确，这只是为了让梯度下降能够运行得更快一点而已。

学习速率的选择

在这一部分，我们将集中讨论一些学习率 α 的选择。具体来说，下图是梯度下降算法的更新规则，你应该还记得吧，这里我想要告诉你如何调试，也就是我认为应该如何确定梯度下降是正常工作的；此外我还想告诉大家如何选择学习率 α：

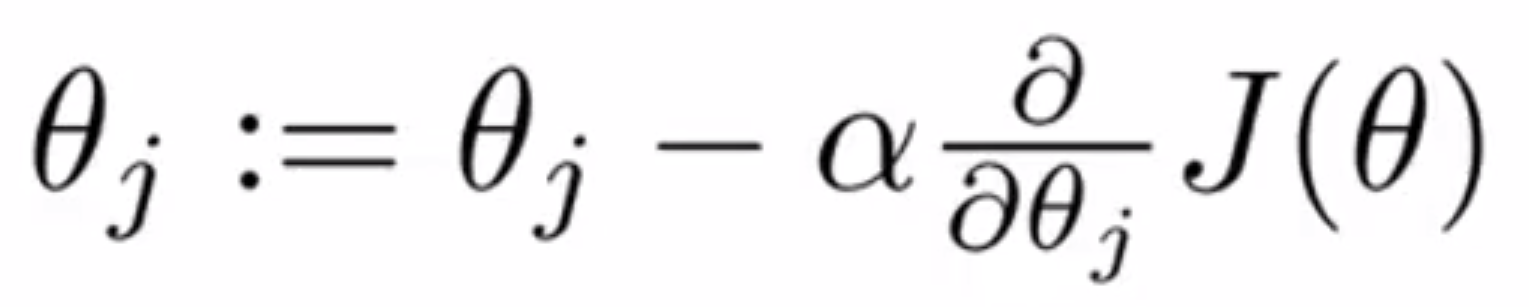
梯度下降算法所做的事情就是为我们找到一个 θ 值(也可能是一个向量)，使得它能够最小化代价函数 J(θ)。我通常会在梯度下降算法运行时通过输出的方式绘出代价函数 J(θ) 的值：

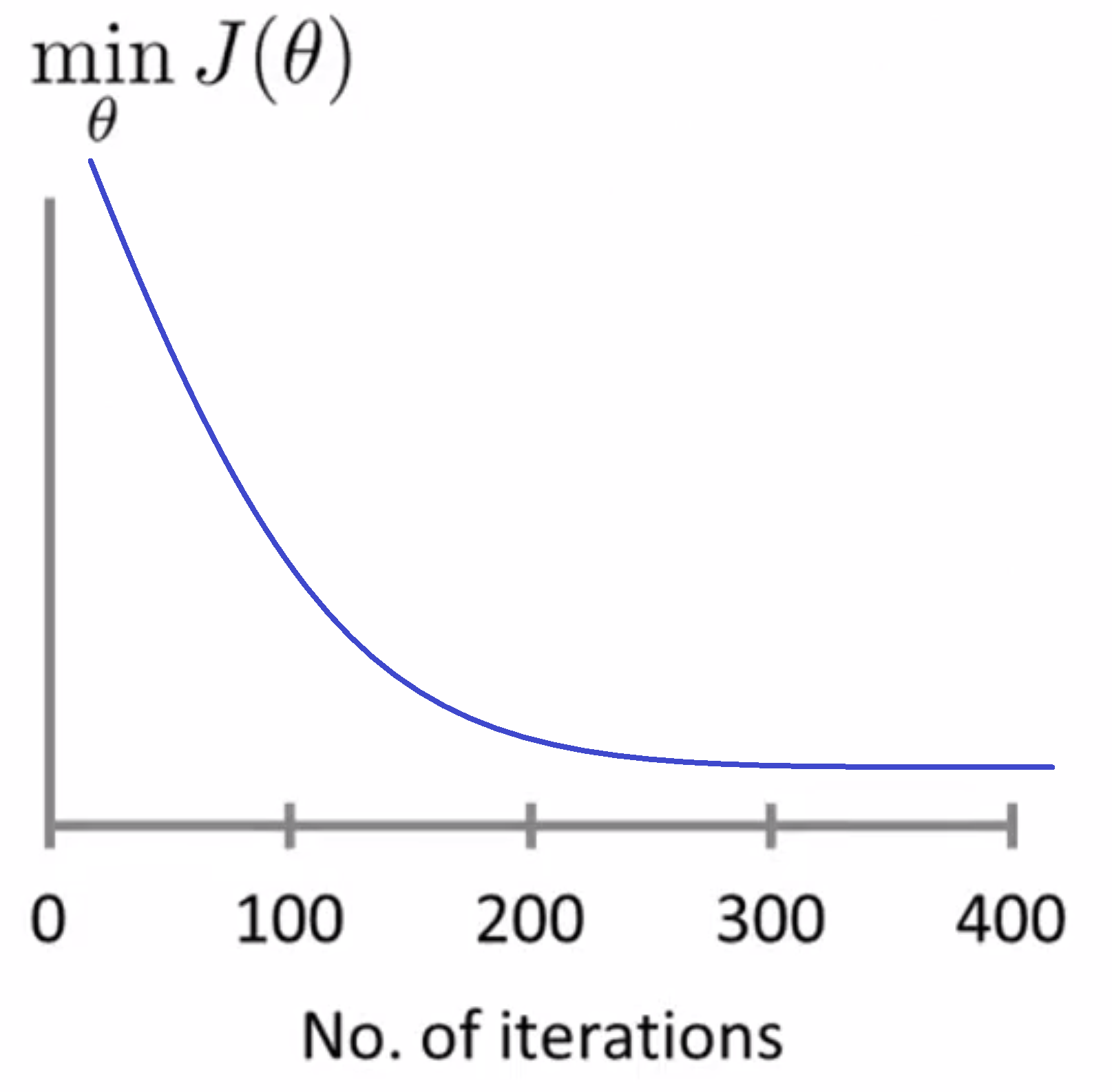
这里的 x 轴是表示梯度下降算法的迭代步数，y轴就是随着梯度下降的 J(θ) 的值，即在每一次迭代之后我将得到一个 θ 值，而我们可以根据这个 θ 值，算出代价函数 J(θ) 的值，而这个点的垂直高度就代表梯度下降算法每一步迭代之后得到的 θ 算出的 J(θ) 值。

如果梯度下降算法正常工作的话，每一步迭代之后 J(θ) 都应该下降。这条曲线的一个用处在于，它可以告诉你，当你达到 300 步迭代之后，也就是300步到400步迭代之间， J(θ) 并没有下降多少，所以当你进行了超过 400 步迭代的时候，这条曲线看起来已经很平坦了，也就是说，在这里400步迭代的时候，梯度下降算法就已经基本上已经收敛了。所以如果能输出数据绘制曲线，可以帮助你判断梯度下降算法是否已经收敛。

顺便说一下，对于每一个特定的问题，每一个数据集，梯度下降算法所需的迭代次数可能会相差很大。也许对于某一个问题梯度下降算法只需要30步迭代就可以收敛，然而换一个问题也许梯度下降算法就需要3000步迭代，再对于另一个机器学习问题，则可能需要30000000000步迭代.实际上我们很难提前判断梯度下降算法需要多少步迭代才能收敛，所以通常我们需要画出这类曲线，画出代价函数随迭代步数数增加的变化曲线再通过观察这种曲线来试着判断梯度下降算法是否已经收敛。

但有的人可能会觉得这太麻烦了，想去偷懒，进行一些自动的收敛测试。也就是说用一种算法，来告诉我们梯度下降算法是否已经收敛。自动收敛测试的一个非常典型的例子是如果代价函数 J(θ) 的下降小于一个很小的值 ε 那么就认为已经收敛。比如所我们可以选择 1e-3 但其实要选择一个合适的阈值 ε 是相当困难的，需要大量的经验。因此为了检查梯度下降算法是否收敛，我们大多数情况下还是可以去以来曲线图，而不是依靠自动收敛测试。

此外这种曲线图也可以在算法没有正常工作时提前警告你。具体地说，如果代价函数 J(θ) 随迭代步数的变化曲线是在不断上升的，比如：

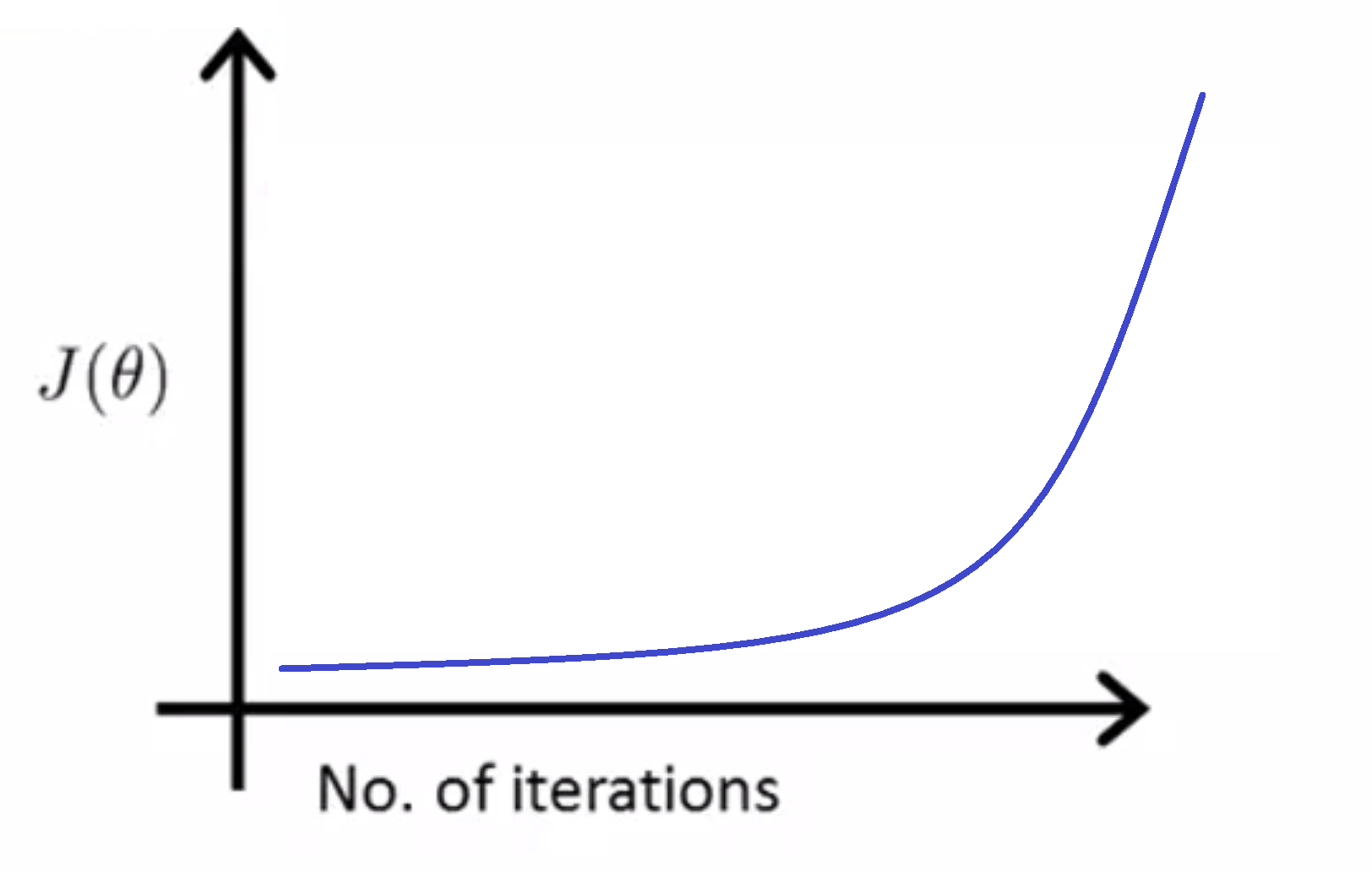
那就证明你的学习速率 α 选择的不太好，很可能是太大了，这时你需要调小你的 α 。就像我们之前提到的那样，会导致发散：

同样地，如果你发现你的 J(θ) 随迭代步数的变化曲线是如下图一样下下上上的，你也同样需要调小你的 α：

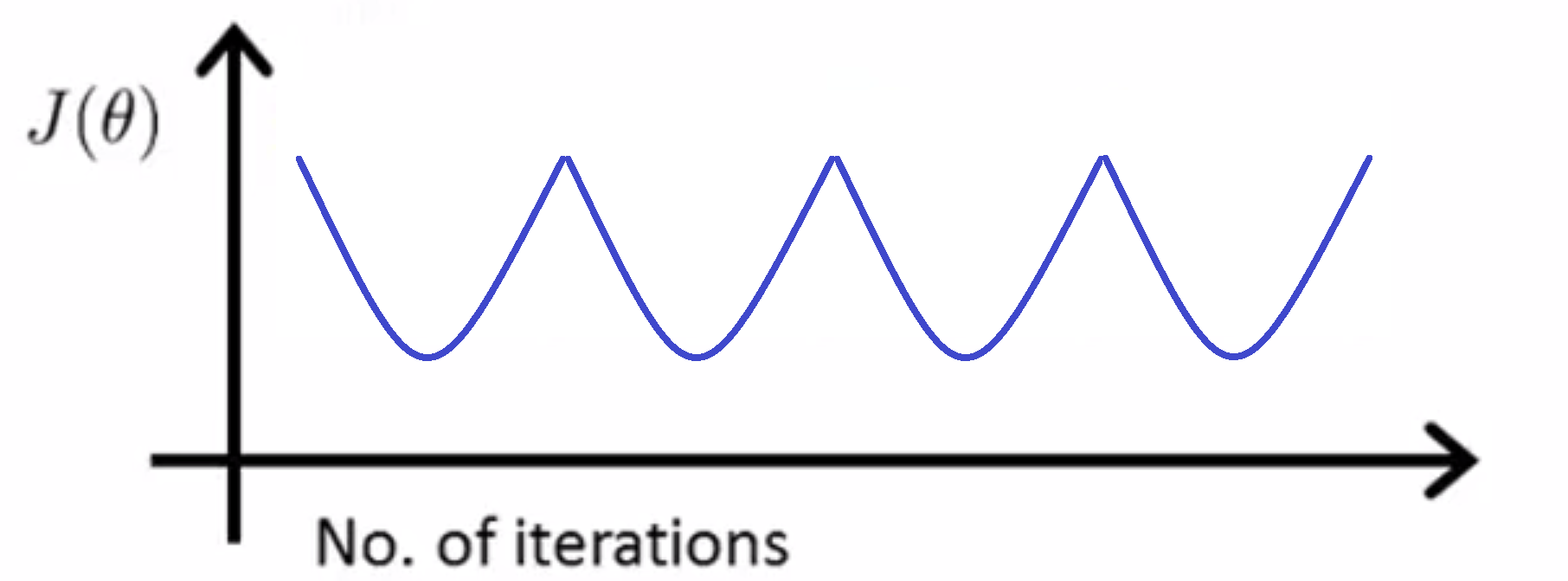
通过数学证明我们可以知道，当 α 足够小的时候，我们的J(θ) 随迭代步数的变化曲线一定是单调下降的。但是这不意味着你可以选取尽量下的 α ，因为如果 α 太小的话，可能会让整个下降过程变得很慢。

具体到 α 的具体选择数值上，我一般习惯在尝试的时候大致以3为一个跨度：……0.1，0.3，1，3，10，30，100……之类的，这样貌似比较容易找到适合的那个 α 。

参数的选择

最后我们来一起康康选择特征的方法，因为当选择了合适的特征后，我们的算法才可能是非常有效的。

我们还是以预测房价为例，假设我们有两个特征，分别是房子长度和宽度，下图就是我们想要卖出的房子的图片，我们就可能会像下面这样建立一个线性回归模型，其中长度是第一个特征值 x1，宽度是第二个特征值x2：

但当我们在运用线性回归时，我们不一定非要直接用给出的 x1 和 x2 作为特征，其实我们也可以自己创造新的特征。比如如果我要预测房子的价格，我们发现真正能决定价格的其实是我房子大小，因此我们可能会创造一个新的特征量x，其值为房子的长度乘以宽度，即x = x1 * x2. 因此特征量的选择其实取决于你从什么样的角度去审视一个特定的问题，而不是只是直接去使用未处理的现成数据，这样可能会使算法的效率更加高，并且有时通过定义新的特征，我们确实可能会得到一个更好的模型。

结语

通过这篇BLOG，相信你已经掌握了一些回归问题的优化方法，快去实现它们吧。最后希望你喜欢这篇BLOG！