在之前的BLOG中我们介绍了单变量的线性回归问题及其解决方法——梯度下降算法，在这篇BLOG中，我们将会从单元走向多元，探讨进一步多元的线性回归问题，并以此为基础学习多项式回归。

多元线性回归

在之前的BLOG中，我们初步介绍了线性回归，特别是单元线性回归，但其实在实际的生活情景中，更多的情况我们往往不止一个变量，所以现在就让我们看看多元线性回归是如何操作的。

在之前我们学习过的线性回归中，我们只有一个单一变量——房屋面积 x 来预测房子的价格，我们的假设函数也是一个只关于单一变量和常数项的一次函数：

但是如果我们不仅有房屋面积作为参数，我们还知道卧室的数量、楼层的数量以及房子的使用年限也与最后的售价有关，这样就给了我们更多可以用来预测房屋价格的信息：

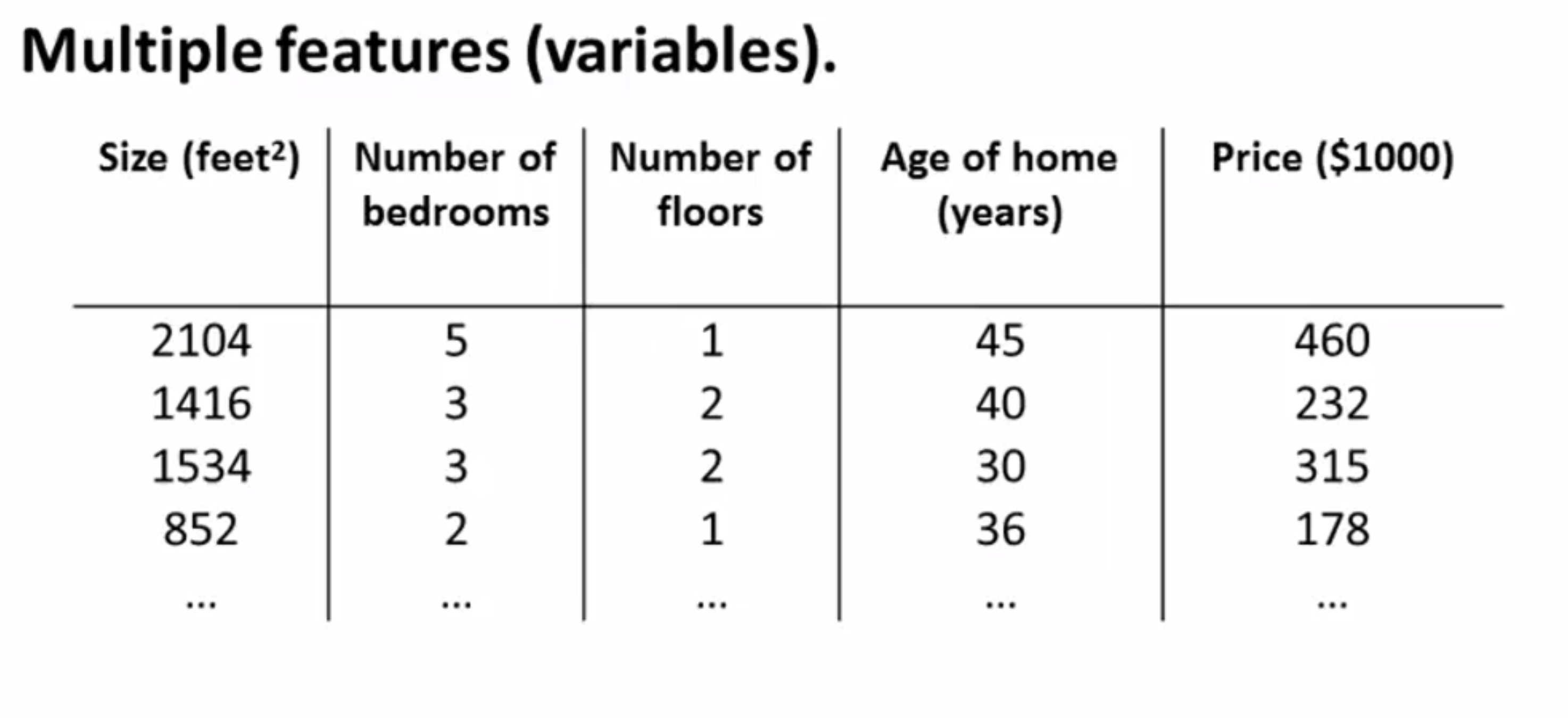
先简单介绍一下在多元线性回归中的一些标记：

在这个例子中，我们有四个特征量——面积，房间的数量，楼层数和房子的年龄，我们分别用 x1，x2，x3，x 4来表示，然后我们依然用 Y 来表示我们所想要预测的输出变量——房屋的价格。

让我们来看看更多的表示方式：

如上，我要用小写 n 来表示特征量的数目，因此在这个例子中，我们的 n 等于 4，因为你们看我们有面积，房间的数量，楼层数和房子的年龄共4个特征量；要值得注意的是，我们之前提到了另一个记号，小写的 m 那是用来表示样本的数量，需要大家加以区分。

上标带 (i) 的 x 来表示第 i 个训练样本的输入特征向量，举个具体的例子，在上面的那个例子中 x 上标 (2) 就是表示第二个训练样本的特征向量，即是向量[1416, 3, 2, 40]，在这里是一个一个四维向量，事实上更普遍地来说这是n维的向量。

接着我用 x 上标 (i) 下标 j 来表示第 i 个训练样本对应的特征向量中的第 j 个特征量，因此具体的来说 x 上标(2) 下标 3 代表着第 2 个训练样本里的第 3 个特征量就等于2。

既然我们有了多个特征量，那我们的假设函数应该是怎样的呢？下图中上面是我们之前使用的假设形式， x 就是唯一的特征量；但看下面那个式子，我们有了多个特征量，我们就不能再使用这种简单的表示方式了，取而代之的，我们将把线性回归的假设，改成 θ0 + θ1 * x1 + θ2 * x2 + θ3 * x3 + …… + θn * xn ：

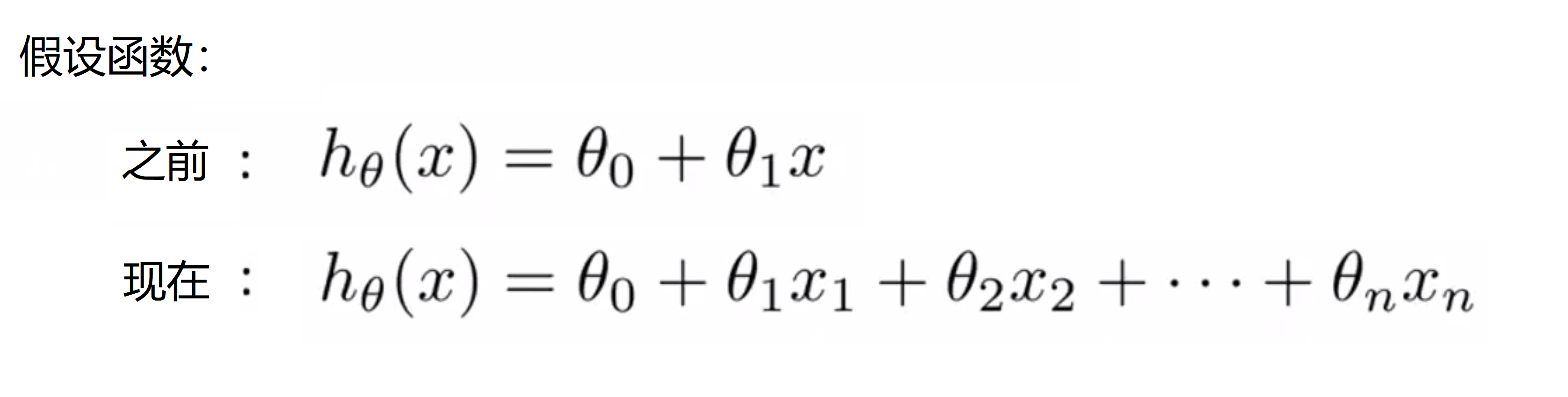
接下来我们来看看如何简化这个等式的表示方式，我们发现上式中只有 x1 到 xn。为了表示方便，我们设置一个 x0 ，其值恒等于1。具体而言，对于第 i 个样本，都有一个向量x(i)，并且 x(i)中的第一个元素(下标0)恒等于 1，所以我现在的特征向量 x 是一个从0开始标记的 n+1 维的向量，而 θ 也可以看成一个n+1 维的向量：

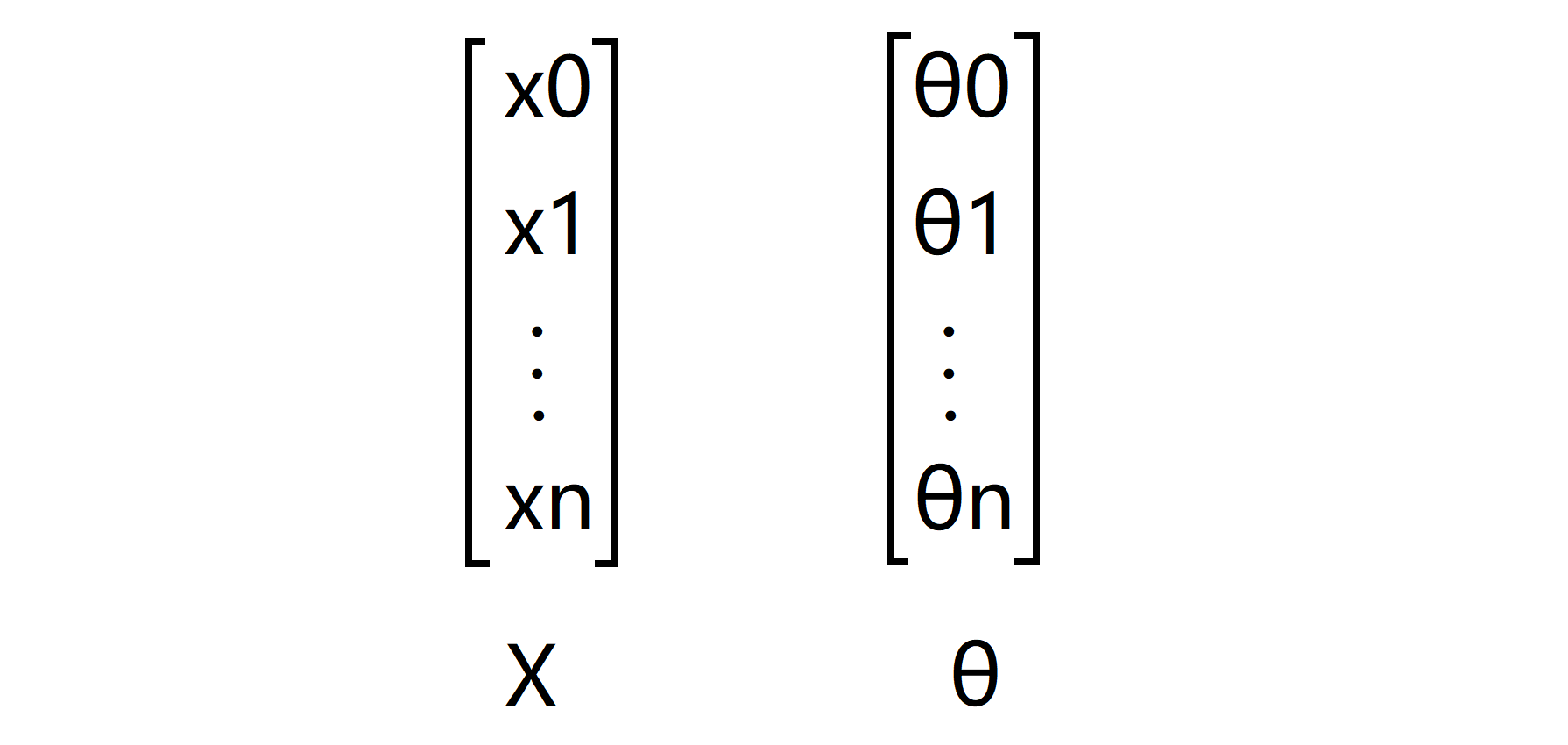
还记得我们之前介绍过转置运算T和向量的内积吧。这是我们发现hθ(x) = θ^T * X,这里的 θ^T 代表 θ 的转置。

而其实所谓的多元线性回归中的多元一词，也就是用来预测的多个特征量或者变量，这只是一种更加好听的说法罢了，不需要这这里花费太多时间去计较。

梯度下降求解过程

在上一部分我们着重介绍了一下多元线性回归的一些概念和记号，而在这一部分我们会一同学习如何使用梯度下降法来解决多特征的线性回归问题。

类似与单元的线性回归，我们同样有：

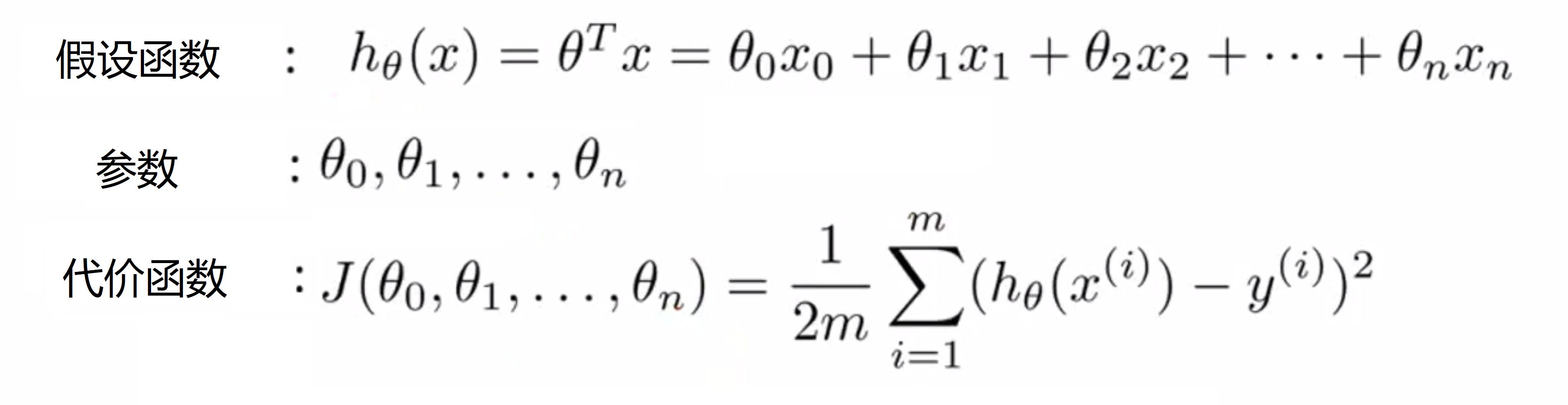
但是其实你也可以把这 n+1 个 θ (θ0 - θn)想象成一个 n+1 维的向量 θ，而原来我们的代价函数是从 θ0 到 θn 的函数 J 并给出了误差项平方的和，但同样地我们也可以把函数 J 想成是一个只关于一个 n+1 维向量的函数，这样就与单元线性回归更加相近了，也更好理解。

接下来我们看看如何使用梯度下降法。类似与单元线性回归，我们将会不停地用 θj 减去 α 倍的一个偏导数项：

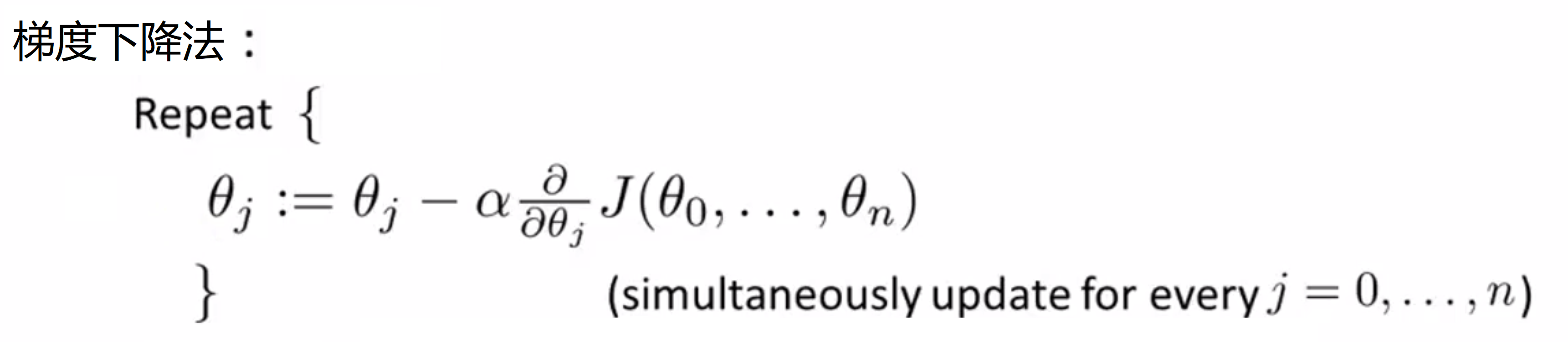
下面是我们当特征 n=1 时的梯度下降的情况，也就是我们熟悉的单元情况，θ0 式子后面打括号的一项就是代价函数相对于 θ0 的偏导数(其实最后那个 1 就是 x0 [还记得我们约定了x0 = 1吗])，同样对参数 θ1 式子后面打括号的一项就是代价函数相对于 θ1 的偏导数(最后那个 x 就是我们所说的 x1)：

现在让我们看看当有一个以上特征时候的算法，通过找规律我们发现，类似地我们有：

我们举个例子对θ0、θ1、θ2的三条更新规则其实就是(记住x0恒为1)：

这样我们就完成了多元线性回归在梯度下降中的算法改写。对上标和下标不太熟悉的可以翻回这篇文章的上一部分再去康康。如果还不理解的同学可以自行推到一下那个偏导数项，相信你会收获很多。

多元回归梯度下降算法实现

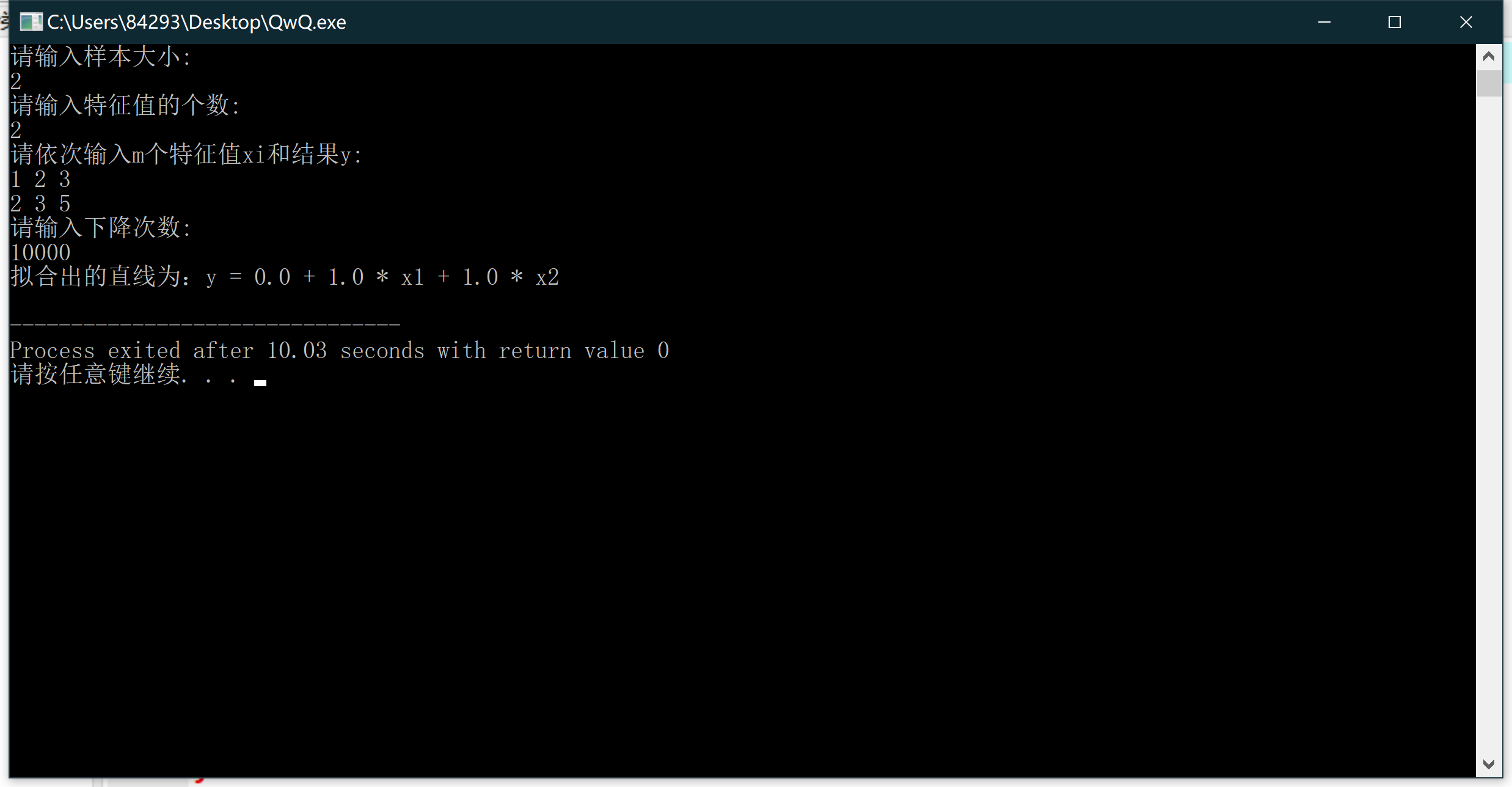
算法的思路都在上面了，同样地，这次我还是用cpp来是实现这个算法供大家交流学习：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
int n, m;
double ans[11000];
double temp[11000], h[11000];
double x[11000][1100], y[11000];
const double Alpha = 3 * 1e-3;
void read() {
    printf("请输入样本大小:\n");
    scanf("%d", &n);

    printf("请输入特征值的个数:\n");
    scanf("%d", &m);

    for(int i = 1; i <= n; i++) x[i][0] = 1;

    printf("请依次输入m个特征值xi和结果y:\n");
    for(int i = 1; i <=n; i++) { 
        for(int j = 1; j <= m; j++) {
            scanf("%lf", &x[i][j]);
        }
        scanf("%lf", &y[i]);
    }
    return;
}

void work() {
    memset(ans, 0, sizeof(ans));
    double delta = 1;
    int num;
    printf("请输入下降次数:\n"); 
    scanf("%d", &num);

    for(int o = 1; o <= num; o++) {
        for(int i = 0; i <= m; i++) temp[i] = ans[i];
        //==========================================
        for(int i = 1; i <= n; i++) {
            h[i] = 0;
            for(int j = 0; j <= m; j++)
            {
                h[i] += x[i][j] * ans[j];
            }
            h[i] -= y[i];
        }
        //==========================================
        for(int i = 0; i <= m; i++) {
            for(int j = 1; j <= n; j++) {
                temp[i] = temp[i] - (Alpha / (double)m) * h[j] * x[j][i];
            }
        }
        //==========================================
        for(int i = 0; i <= m; i++) ans[i] = temp[i];
    }
    return ;
}

void write() {
    printf("拟合出的直线为：");
    printf("y = %0.1lf", ans[0]);
    for(int i = 1; i <= m; i++) {
        if(ans[i] >= 0)printf(" + %0.1f * x%d", ans[i], i);
        else printf(" - %0.1f * x%d", -ans[i], i);
    }
    printf("\n");
}
int main() {

    read();
    work();
    write();
    return 0;
}  

其效果也是极为不错的：

多项式回归

在之前的学习中，我们一直都在用直线也就是一次函数来拟合数据，但是实际情况中，我们最好的拟合方案可能不是一个一次函数，而是一个二次，三次，根号，log之类的多项式。

比如下面这个例子，用直线来拟合显然是不太正确的：

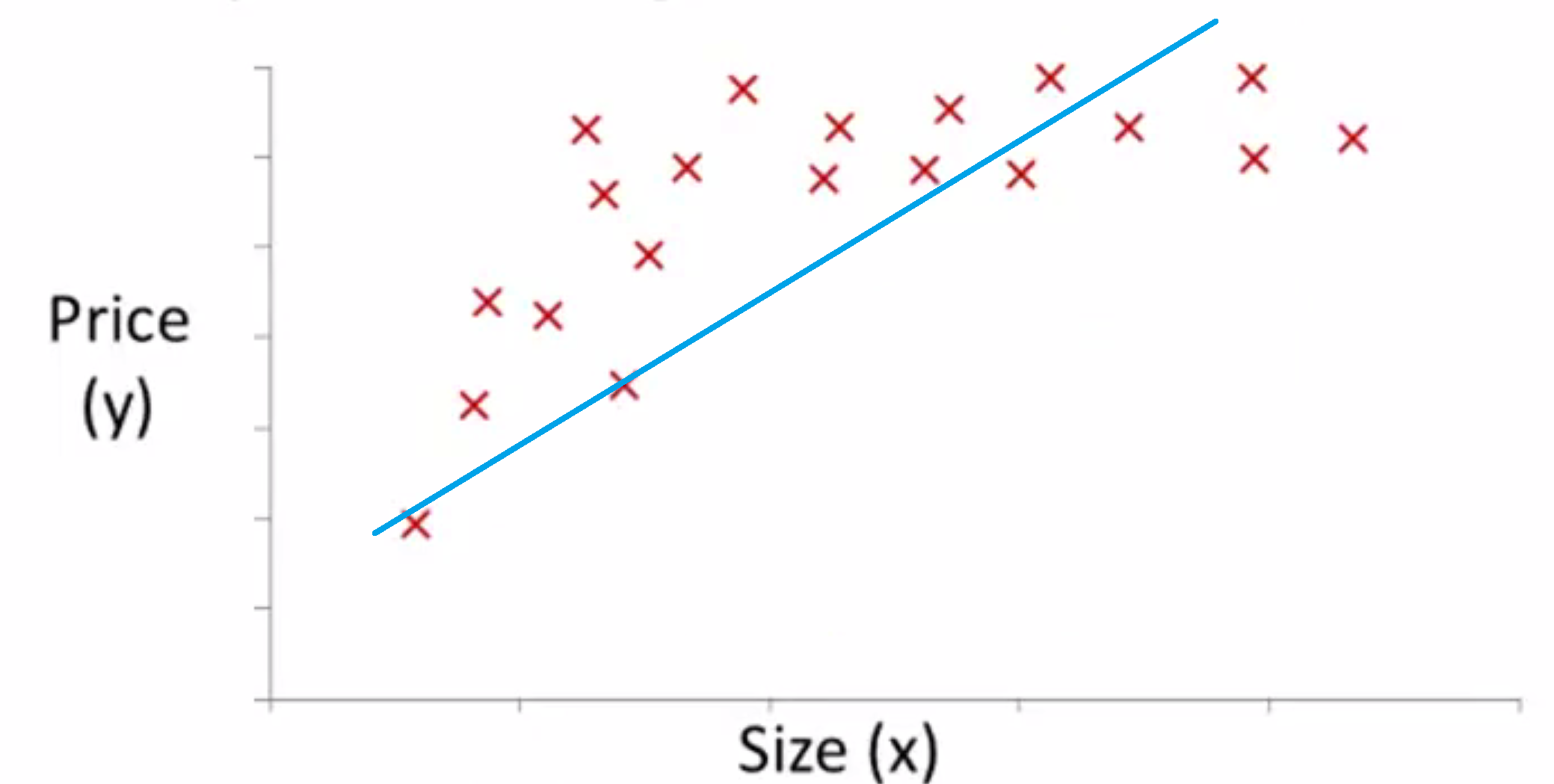
而如果我们使用一个关于常数项和 √x 或者三次多项式之类的的多项式来拟合，结果可能会好得多：

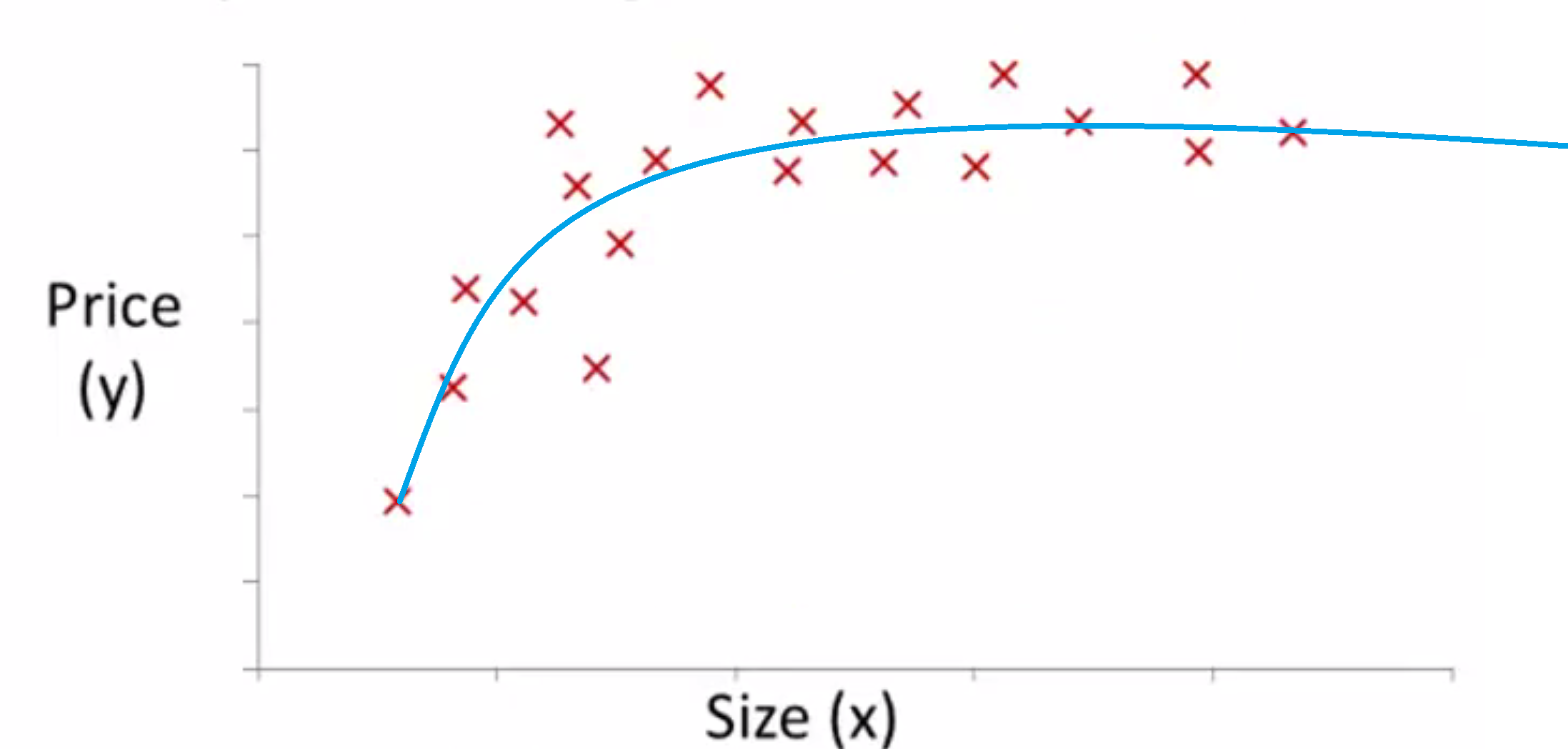
那我们怎么用已经学过的知识来实现使用多项式回归呢？其实我们可以用多元线性回归的方法。我们可以通过将我们的算法做一个非常简单的修改来实现它，以按照我们以前假设的形式对这样的模型进行拟合。

假如我确定要用三次函数去拟合这些数据，那么我们可以：

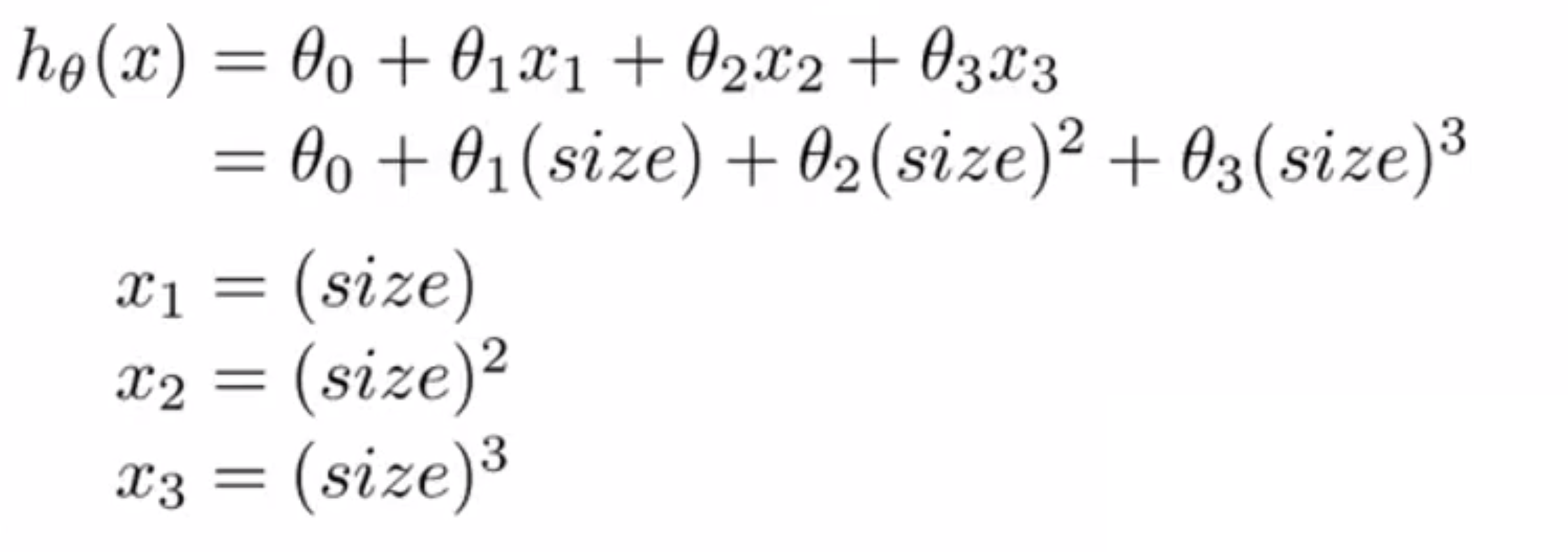
将 x1 特征设为房子的面积，将第二个特征 x2 设 房屋面积的平方，将第三个特征 x3 设为房子面积的立方，然后再应用多元线性回归的方法就可以完成拟合。

然后如果我们像这样选择特征，那么几个特征值的范围差距就很大(指数级)，那么特征的归一化就变得更重要了，这可以加速我们梯度下降的过程，至于具体怎么优化，在下一篇BLOG我会重点介绍。

但是除了建立一个三次模型以外，我们也许有其他的选择，比如log，根号之类的，这就要我们去慢慢猜测了。

当然在之后的学习中，我们将会学到一些更加高级的算法能够自动选择要使用什么特征，即它可以观察给出的数据并自动为你选择到底应该选择一个二次函数或者一个三次函数还是别的函数。当然在现阶段，通过观察加多项式回归拟合的方法就能得到一个比较符合你的数据的模型。

结语

通过这篇BLOG，相信你已经初步掌握了多元线性回归及多项式回归，希望你能好好地运用这些工具。最后希望你喜欢这篇BLOG！