在之前的BLOG里，我们已经基本学完了计算几何的算法。可是仍然有一些题目是我们之前的算法所无法解决的。这时候我们就要使用计算几何的终极奥义——枚举和分治 :neckbeard:。

枚举与计算几何

先引入一道经典例题：

[caioj 1211]统计正方形

题目描述
【题目描述】
给定平面上N个点,你需要计算以其中4个点为顶点的正方形的个数。注意这里的正方形边不一定需要和坐标轴平行。
【输入文件】
第一行一个数N,以下N个点的坐标。
【输出文件】
一个数正方形的个数。
【样例输入】
7
0 0
0 1
1 0
1 1
1 2
2 1
2 2
【样例输出】
3
【数据规模】
对于20％的数据,满足1≤N≤20；
对于l00％的数据,满足1≤N≤500,-50≤X[i],Y[i]≤50,点不会重叠。

看到这道题，很多同学就有些蒙了，好像叉积凸包旋转卡壳都用不上了。但冷静一下，看一下数据范围，呀！1≤N≤500。这就引导我们往O(n^2)的枚举判断去思考了。

我们知道如果知道了正方形的任意两点的坐标，就可以推出其余两个点的坐标。为了方便起见，我们枚举正方形中靠下的两个点分别设为 I(xi,yi) 和 J(xj,yj) （规定其中J的横坐标xj大于I的横坐标xi）。

然后我们令X=xj-xi；Y=yj-yi；
接着我们就可以推出剩下两点坐标：
O(xi-Y,yi+x)，P(xj-y,yj+x);只需要用数组判断O，P两点是否存在即可，若存在则ans++，否则继续枚举下一个I，J。(如下图)

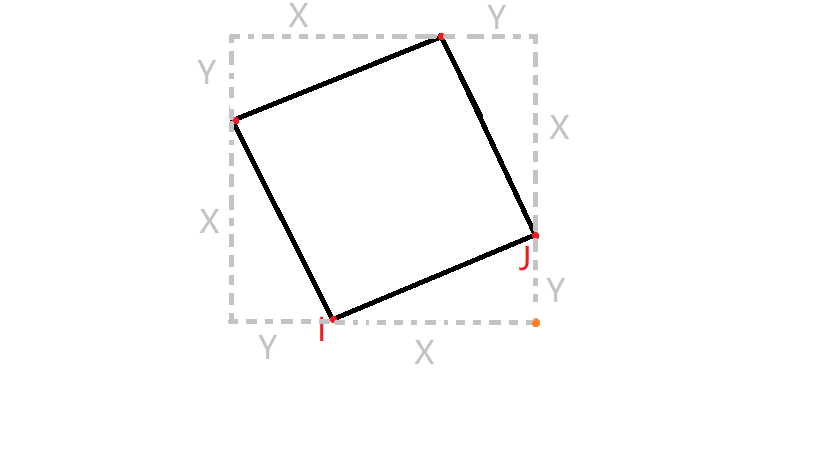
特别需要注意的是，由于坐标可能为负数，为了方便后面的判断，需要让每个点的坐标加上一个比较大的正数让坐标全部变为正数，具体代码如下：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
    int x,y;
}a[1100];
int f[1100][1100]={0};
int i,j,k,m,n,o,p,u,v,ans;

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&u,&v);
        a[i].x=u+500;
        a[i].y=v+500;

        f[a[i].x][a[i].y]=1;
    }

    ans=0;

    for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
    if(i!=j)
    {
        if(a[i].x<a[j].x)if(a[i].y<=a[j].y)
        {
            int x=a[j].x-a[i].x;
            int y=a[j].y-a[i].y;

            if(f[a[i].x-y][a[i].y+x]==1)
            if(f[a[j].x-y][a[j].y+x]==1)
            ans++;
        }
    }

    printf("%d",ans);
}

*分治与计算几何

在上一篇BLOG中，我们用旋转卡壳算法实现了O(n)求解平面内的最远点对，那最近的点对呢？暴力枚举的复杂度达到了O(n^2),要想更优地解决这个问题，我们不妨先把问题简化，看看一维上这个问题的求解方法。

一维内的最近点对

此时，n个点退化为x轴上的n个实数x1，x2，...，xn。最接近点对即为这n个实数中相差最小的两个实数。显然可以先将点排好序，然后用O(n)线性扫描就可以了。但我们为了便于推广到二维的情形，尝试用分治法解决这个问题。

首先肯定要先对点进行排序，接着假设我们用m点将S分为S1和S2两个集合，这样一来，对于所有的p(S1中的点)和q(S2中的点)，有p小于q。

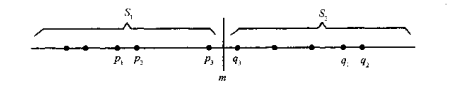
然后把s1和s2分别当作完整的序列s，重复上述操作，递归地在S1和S2上找出其最近点对{p1,p2}和{q1,q2}，并设
d = min{ |p1-p2| , |q1-q2| }

由此易知，S中最近点对可能是{p1,p2}，可能是{q1,q2}，也可能是某个{q3,p3}，如上图所示。

如果此时最近点对是{q3,p3}，即|p3-q3|小于d，则p3和q3两者与m的距离都不超过d，且p3和q3一定分别出现在区间(m-d,d]和(d,m+d]。此时，一维情形下的最近点对时间复杂度为O(nlogn)。

二维内的最近点对

其实我们可以对刚刚的做法进行推广，我们可以首先先对x坐标进行排序，取出中点，然后对于左右两边的区域s1，s2，重复上述过程，递归地求出左右两边分别的最近点对的距离d1，d2，并且令d=min(d1,d2)。

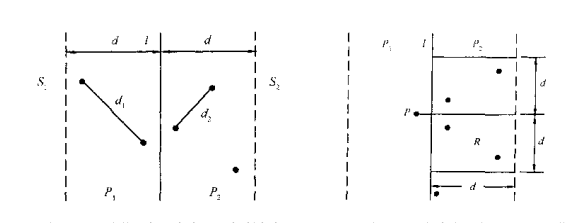
接着我们来考虑中间的情况，由左图可见，由于可能的点只会落在（mid-d，mid+d）的宽为2d的带状区间内，但最多可能有n个点，合并时间最坏情况下为n^2。但是，P1和P2中的点具有一种神奇的稀疏的性质——对于P1中的任意一点，P2中的点必定落在一个d*2d(如右图，不然P1，P2之间的距离d3一定大于d)的矩形中，且最多只需检查六个点（鸽巢原理，最后我会给出完整证明）。这样，先将带状区间的点按y坐标排序，然后线性扫描，这样合并的时间复杂度为O(nlogn)，几乎为线性。所以总的时间复杂度为O(nlognlogn)。

对于最多六个节点的证明

我们继续用回上一幅图进行证明；

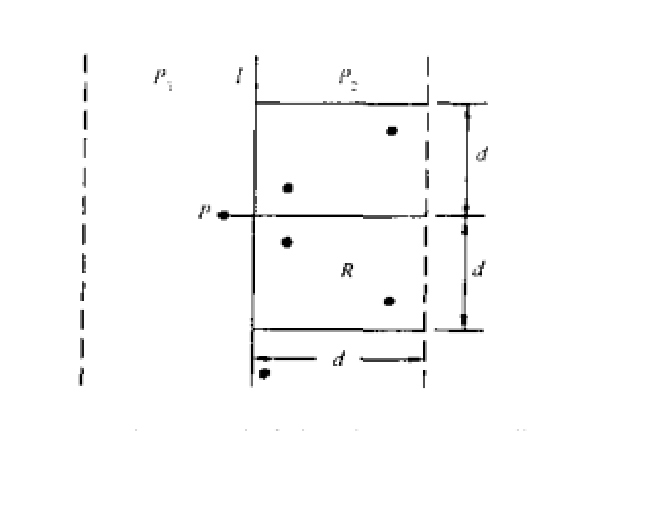
我们知道，左右两边分别的最近点对的距离d1，d2，并且令d=min(d1,d2)，也就是右边这个d2d的矩形中，任意两点的之间的距离都要大于等于d。那么我们想在这个d2d的矩形中放尽量多的点，但彼此之间距离都要大于等于d，怎么放呢？

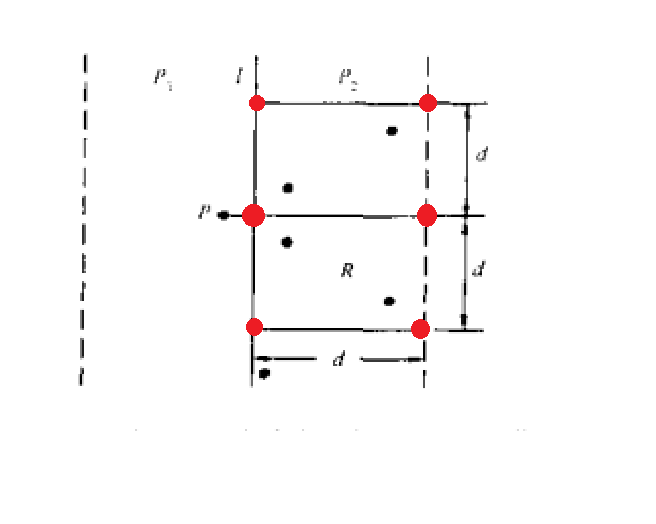
聪明的你一定想到了，按照上图的红点位置放，是最优的策略了。但此时最多也就只能放下六个点。所以原结论是正确的。

再来道模板题

[caioj 1206]最近点对的距离

【题意】
给出n个点的坐标，求最近两点间的距离。
【输入格式】
第一行一个整数n(2 ≤ n ≤ 50000)。
下来n行，每行两个实数x和y表示点坐标。
【输出格式】
一行一个实数，表示最近两点间的距离（保留4位小数）。
【样例输入】
5
0 0
0 5
5 0
5 5
2 0
【样例输出】
2.0000

直接贴模板了：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
    double x,y;
}p[51000],f[51000];

int i,j,k,m,n,o;
double ans,lans,rans;

double dis(node x,node y)
{
    return (sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y)));
}

double my_min(double x,double y)
{
    if(x<y)return(x);
    else return(y);
}

bool cmp(node x,node y)
{
    if(x.x<y.x)return(true);
    return(false);
}

bool cmpp(node x,node y)
{
    if(x.y<y.y)return(true);
    return(false);
}

double close(int left,int right)
{
    if(left==right)return(21474836);//只有一个点的情况 
    if(left+1==right)//只有两个点的情况 
    {
        return(dis(p[left],p[right]));
    }

    int mid=(left+right)/2;
    double d1=close(left,mid);
    double d2=close(mid+1,right);
    //递归分别求出左右两块区域s1，s2的最近距离d1，d2 
    double d=min(d1,d2);
    int len=0;

    for(int i=left;i<=right;i++)
    if(fabs(p[i].x-p[mid].x)<=d)
    f[++len]=p[i];

    sort(f+1,f+len+1,cmpp);
    //选出mid左右d的条状区域的所有点并且按照y轴坐标排序 
    for(int i=1;i<len;i++)
    {
        for(int j=i+1;j<=len;j++)
        if(f[j].y-f[i].y<d)
        {
            double d3=dis(f[i],f[j]);
            if(d3<d)d=d3;
        }
        else break;//利用鹊巢原理进行优化 
    }
    //判断是否有小于d的值存在 
    return(d);
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%lf%lf",&p[i].x,&p[i].y);
    sort(p+1,p+n+1,cmp);//对于x轴坐标排序 

    ans=close(1,n);//计算答案 

    printf("%0.4lf",ans);
    return 0;
}

结语

到这里，计算几何的基本算法我都介绍完了，计算几何可能就先告一段落了（以后看到其他题型再来补充）。期待下一个专题吧！感谢你的阅读！