不知不觉简单的计算几何就快讲完了，这次我再讲讲旋转卡壳算法（看得我脑袋是有些卡壳QwQ）。这个算法和凸包有着很大的关系，所以建议没看凸包的同学去计算几何分类看一下凸包的求解方法。

先抛出一个问题

在二维平面上给定n个点，求距离最远的两个点之间的距离是多少？
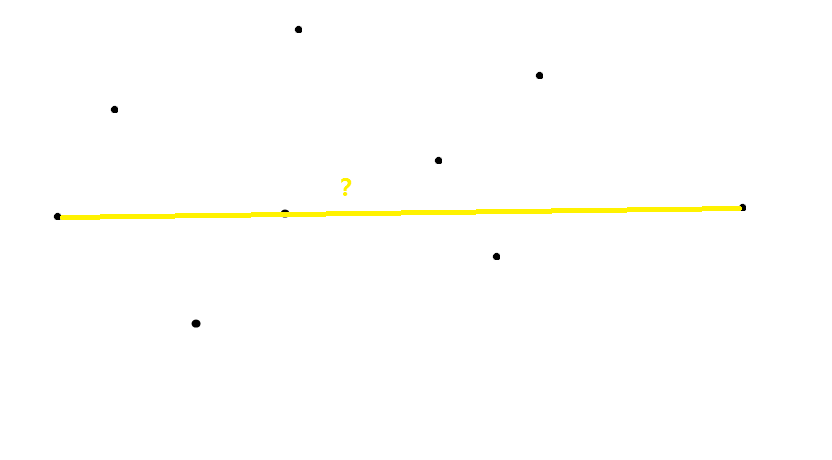
xz1.png
看到这道题，大部分同学第一反应肯定是暴力——暴力枚举所有点对，然后求出最远的那一对相距的距离。这种方法当然没错，可是复杂度已经达到了O(n^2)，当n是50000,100000，甚至1000000时，暴力就显得苍白无力。

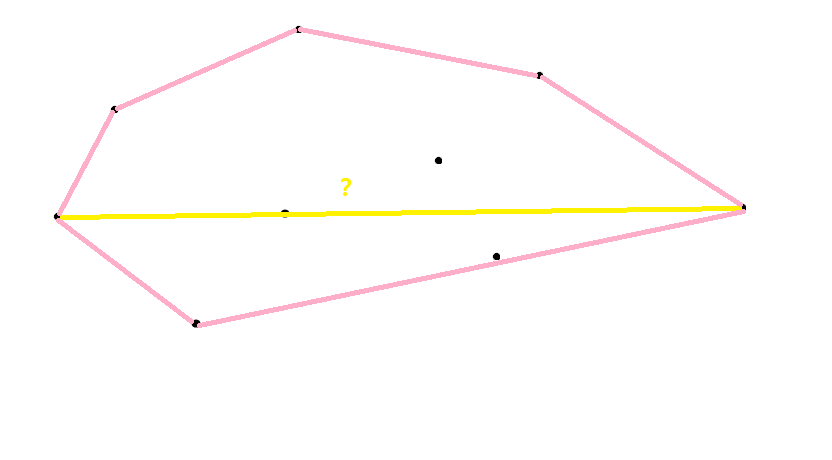
这时我们进一步思考，这个最远点对一定会出现在这些点集的凸包上，所以在这里我们在凸包上，使用复杂度低至O(n)的旋转卡壳算法进行求解。
xz2.png

什么是旋转卡壳算法

旋转卡(qiǎ)壳算法:是解决一些与凸包有关问题的有效算法，计算时就像一对平行卡壳卡住凸包旋转而得名。

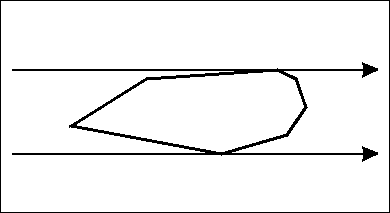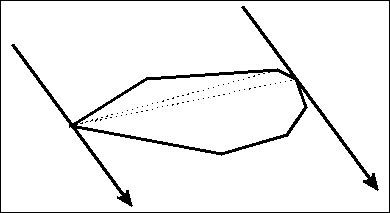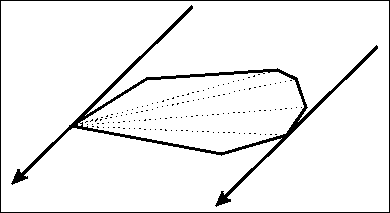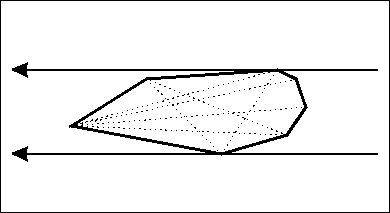
xz.gif
【图片来自:http://cgm.cs.mcgill.ca/~orm/rotcal.html 】

在凸包上，被一对平行卡壳正好卡住的对应点对称为对踵点；可以证明对踵点的个数不超过3n/2个 也就是说对踵点的个数是O(n)的，对踵点的个数也是我们下面解决问题时间复杂度的保证。

我们发现，平行卡壳分为两种情况：
(1)卡住两个点：
xz3.png
(2)卡住一条边和一个点：
xz4.png

由于在处理过程中，卡壳卡住两个点的情况不好处理，所以一般我们都是去关注第二种情况。在这种情况下我们发现，一个对踵点到对应边之间的距离比其他点要大。
也就是说，一个对踵点和对应边所形成的三角形的面积是最大的，所以我们可以使用叉积的第二种用法——求三角形面积来求解对踵点。

经过比对我们发现，对踵点对距离中的最大值，就是在这个二维平面内两点距离的最大值，总的时间复杂度为O(n)。

怎样实现旋转卡壳算法

首先，由于旋转卡壳算法是建立在凸包上的，我们要先对所有点求出一个凸包，放在数组(设为sta数组)内，由于之前已经细细讲过凸包了，这里就不做细讲，不懂凸包的同学请先移步二维凸包。

现在我们需要考虑，如何得到距离每条对应边的的最远点呢?稍加分析,我们可以发现,我们可以把点到直线的距离化解为三角形的面积，再运用叉积进行比较。同时，凸包上的点依次与对应边产生的距离成单峰函数,面积上升到最高点后，又会下降。(具体证明可以从凸包定义入手 用反证法解决)
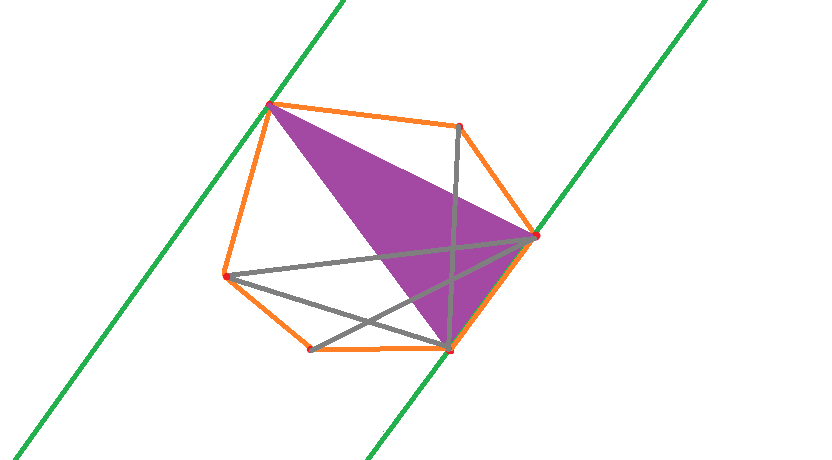
xz6.png

利用单峰函数这一性质，我们可以根据凸包上点的顺序，枚举对踵点，直到下一个点的距离小于当前点就可以停止了，而且随着对应边的旋转，最远点也只会顺着这个方向旋转，我们可以从上一次的对踵点开始继续寻找这一次的。由于内层while循环的执行次数取决于j增加次数 j最多增加O(n)次，所以求出所有对踵点的时间复杂度为O(n)。
代码如下：

    sta[top+1]=sta[1];j=2;ans=0;
    for(int i=1;i<=top;i++)
    {
        while(fabs(multi(sta[i],sta[i+1],sta[j]))<fabs(multi(sta[i],sta[i+1],sta[j+1])))
        {
            j++;
            if(j>top)j=1;
        }
        //js=dis(sta[i],sta[j]); 错误版本
        js=max(dis(sta[i],sta[j]), dis(sta[i+1],sta[j]));
        if(js>ans)ans=js;
    }

简单的模板题

【caioj 1226】最远点对的距离

题目描述
【题意】
给出n个点的坐标，求最远两点间的距离。
【输入格式】
第一行一个整数n(2 ≤ n ≤ 50000)。
下来n行，每行两个实数x和y表示点坐标（x,y<=|10^6|)。
【输出格式】
一行一个实数，表示最远两点间的距离的平方（保留2位小数）。
【样例输入】
5
0 0
0 5
5 0
5 5
2 0
【样例输出】
50.00

这就是一道经典的模板题。只要凸包再跑一遍旋转卡壳算法就可以完美求解了。
附上代码（同时也是模板），并特别感谢fatzard和fiora_gwx对代码的指正：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
    double x,y;
}p[510000],sta[510000];

int i,j,k,m,n,o,top;
double ans,jl,js;

double multi(node p1,node p2, node p0)
{
    double x1=p1.x-p0.x;
    double y1=p1.y-p0.y; 

    double x2=p2.x-p0.x;
    double y2=p2.y-p0.y;

    return(x1*y2-x2*y1); 
}//计算叉积 

double dis(node p1,node p2)
{
    return (double((p1.x-p2.x)*(p1.x-p2.x))+double((p1.y-p2.y)*(p1.y-p2.y)));
}//计算任意两点间距离 

bool cmp(node p1,node p2)
{
    double tt=multi(p1,p2,p[1]);
    if(tt<0)return(0);
    if(tt==0 && dis(p1,p[1])>dis(p2,p[1]))return(0);
    return(1);
}

void graham()
{
    sort(p+2,p+n+1,cmp);
    for(int i=1;i<=2;i++)sta[i]=p[i];
    top=2;
    n++;p[n]=p[1];

    for(int i=3;i<=n;i++)
    {
        while(top>1 && multi(sta[top],p[i],sta[top-1])<=0)top--;
        top++;
        sta[top]=p[i];

    }
}

int main()
{

    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%lf%lf",&p[i].x,&p[i].y);
        if(p[i].y<p[1].y ||(p[i].y==p[1].y && p[i].x<p[1].x))
        {
            node t=p[1];p[1]=p[i];p[i]=t;
        }//找最下方的点 
    }

    top=0;//记录凸包上点的个数 
    graham();
    top--;//sta中存储了top+1个点，第top+1个和第一个相同 

    j=2;ans=0;
    for(int i=1;i<top;i++)
    {
        while(fabs(multi(sta[i],sta[i+1],sta[j]))<fabs(multi(sta[i],sta[i+1],sta[j+1])))
        {
            j++;
            if(j>top)j=1;
        }
        js=max(dis(sta[i],sta[j]), dis(sta[i+1],sta[j]));
        if(js>ans)ans=js;
    }//旋转卡壳

    printf("%0.2lf",ans);
    return 0;
}

结语

通过这篇博客，我相信神犇的你一定已经熟练的掌握旋转卡壳算法了，到这里计算几何也差不多接近尾声了，莫名有些悲伤:cry:。最后感谢你阅读这篇博客！

Last modification：March 17th, 2022 at 04:10 pm
© 允许规范转载
If you think my article is useful to you, please feel free to appreciate