上学期的新手赛和CSP被各路大佬吊打QwQ,在复习的时候发现还有KD树这个数据结构没有了解过,所以今天就让我们一起来学习多维查找树-KD树吧。PS不知不觉就第100篇BLOG了有点激动!!!
什么是KD树
KD树是K-dimension tree的缩写,是对数据点在k维空间(如二维(x,y),三维(x,y,z),k维(x1,x2,……,xk))进行划分的一种数据结构,主要应用于索引结构中相似性查询,其中包含两种基本的方式:一种是范围查询,范围查询时给定查询点和查询距离阈值,从数据集中查找所有与查询点距离小于阈值的数据;另一种是K近邻查询,就是给定查询点及正整数K,从数据集中找到距离查询点最近的K个数据,当K=1时,它就是最近邻查询。
从本质上来说,Kd-树就是一种平衡二叉树。所以在学习KD树之前,就先让我们先复习一下平衡二叉树。所谓二叉查找树,就是一种具有以下性质的二叉树:
若它的左子树不为空,则它的左子树节点上的值皆小于它的根节点。
若它的右子树不为空,则它的右子树节点上的值皆大于它的根节点。
它的左右子树也分别是二叉查找树。
若你之前没有了解过二叉查找树,可以点击这里进行深度学习。
其实二叉查找树是对一维的数据进行的线性划分,而KD树则是它的升级版,其划分的是一个空间。换句话说,KD树就是把数据所在的空间划分为特定的几个部分,然后在特定空间的部分内进行相关搜索操作:
可能到这你都还觉得很抽象不好理解,没关系下面我就通过两个具体实例来分别构造解决这两种问题的KD树。
范围查找的应用
先思考一个问题
假如在一款叫做《蒟蒻联盟》的游戏中,给你 n(n≤1e5)个角色,告诉你每个角色的攻击力ai和防御力di。然后有m(m≤1e5)次询问,每次询问给定al,ar,dl,dr,要求输出攻击力在[al,ar],防御力在[dl,dr]之间的角色数量。
乍一看题目好像无从下手,没关系我们先试着把题目简化一下。假如数据范围不变,我们每个角色只知道攻击力信息,并且每次查询的限定也只是攻击力在[al,ar]而已,那我们应该怎么做呢?
如果每次查询都遍历一遍所有角色进行判断,那我们的复杂度就是O(nm),是铁定会TLE的。根据数据范围感性判断,我们单次查询的复杂度要控制在O(logn),所以我们可以考虑树状的数据结果。想到这里,答案其实已经呼之欲出了,没错,就是构建二叉查找树。
假设我们有 6 个角色,第 i 个角色的攻击力与防御力属性构成类似 (ai, di) 的元组,就假设我们六个角色的数据分别为 (2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)吧;那么在简化的问题中,我们只考虑攻击机,即每个角色的前一个属性——2, 5, 9, 4, 8, 7,我们如何构造二叉查找树呢?
相信你已经学会了二叉查找树这个前置知识,那么我们直接来看看构造出来的二叉查找树的样子:
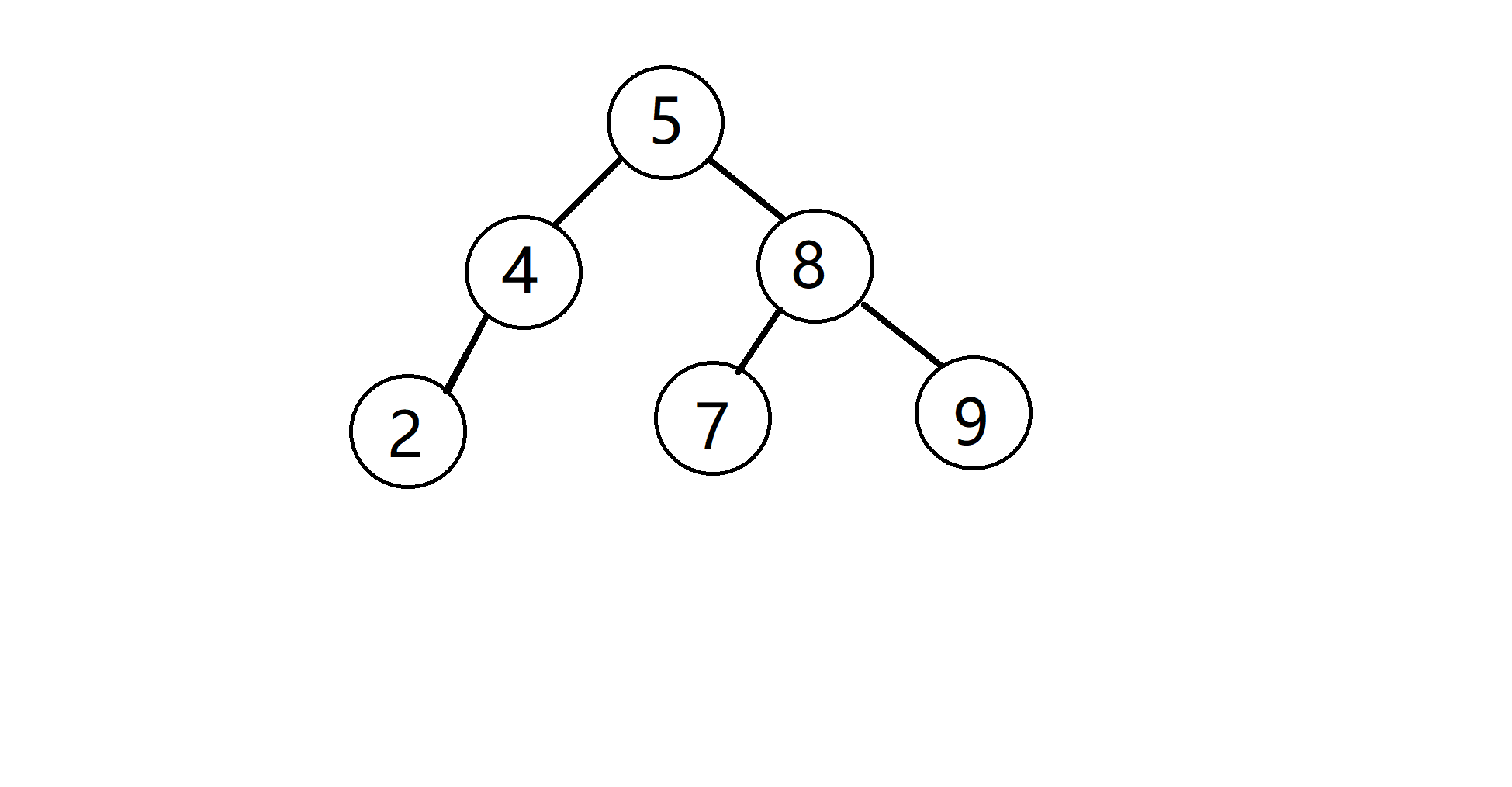
接着假如我们要查找攻击力在[1, 4]范围内的角色,我们只要按照二叉查找树的性质,找到对应的子树就可以了:
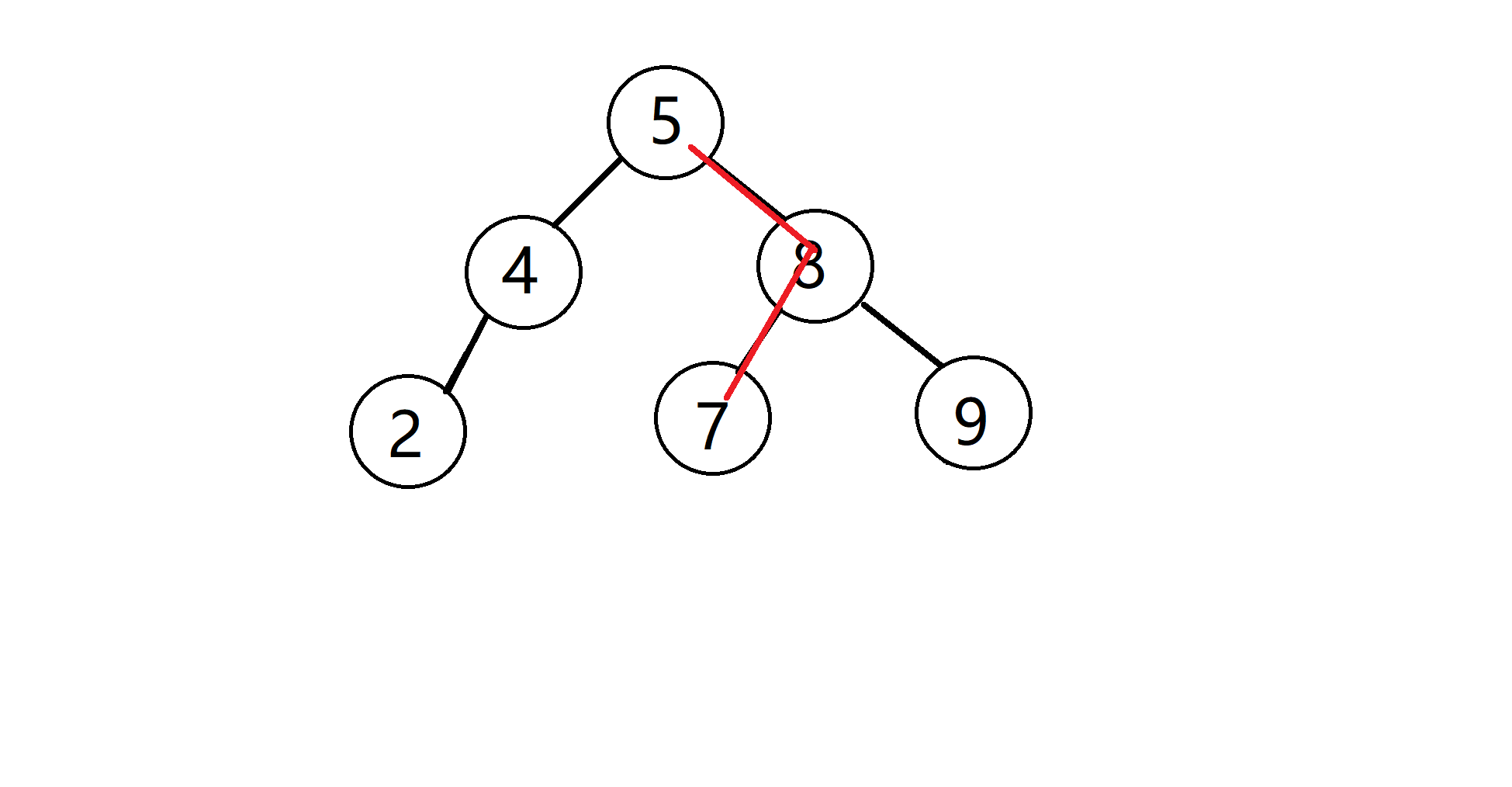
我们可以看到普通的二叉查找树其实是对一维数据的划分(划分顺序为红绿蓝):
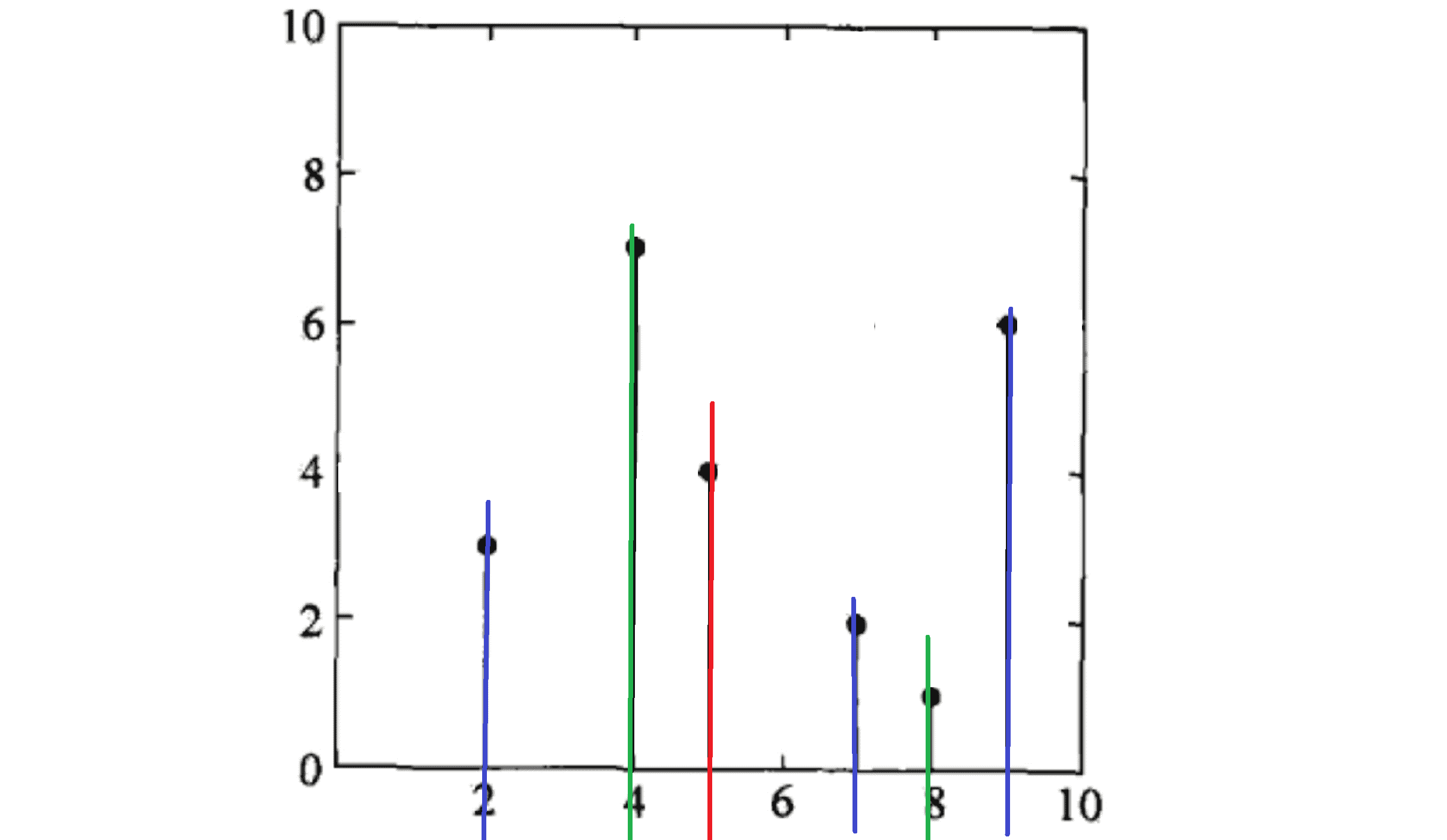
那我们加大题目难度,这时我们要查找攻击力在[al,ar],防御力在[dl,dr]之间的角色数量怎么办?有一种很简单的想法,就是建立两棵二叉查找树,分别维护攻击力和防御力,然后先找到攻击力在[al,ar]的角色集合S1,再找到防御力在[dl,dr]的角色集合S2,然后计算S1和S2的交集就是我们的答案。但是这样做的话,最坏情况单次也要O(n),最坏情况下总的复杂度就到了O(nm)。
那我们有没有更加优秀的针对多维数据的查找算法呢?没错就是KD树,下面我们就沿用上面这个二维数据的例子对KD树进行讲解。
KD树
KD树的构建
实现原理
二叉查找树做的是对一维数据的划分,而KD树做的是对多维数据的划分,但其最后表现在树上都是一棵二叉树。下面我们就通过例子看看KD树是如何划分空间的。
我们的数据(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)在二维平面下的表示大致如下图:
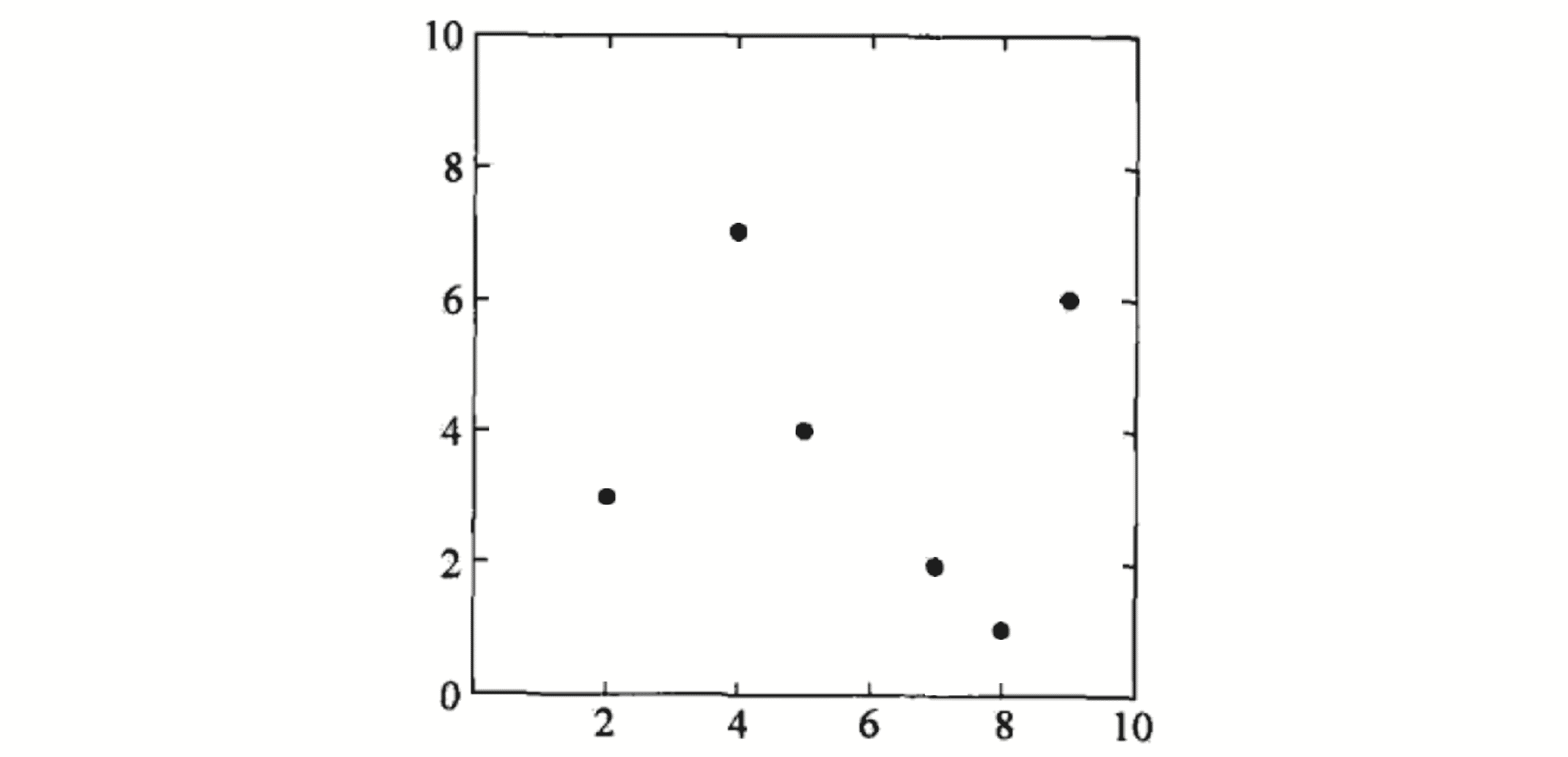
为了方便后续说明我们设攻击力表示为x0,防御力表示为x1。这图中的横轴代表的是 x0,纵轴代表的是 x1。顺带一提,若我们需要处理的是 n 维数据,我们一般表示为(x0, x1, x2, x3 …… xn-1)。
我们的最终目标是把上图中的六个点划分到不同的平面区域内,那如何划分呢?一般来说,假如我们的数据是 n 维,那么对于第 j 层划分,我们设 l = j % n,我们当层划分的就是 xl 这个维度,而划分的地方就是划分区域的待划分点在 xl 这个维度的“中位数”。对于我们《蒟蒻联盟》的数据,划分的最后结果如下:
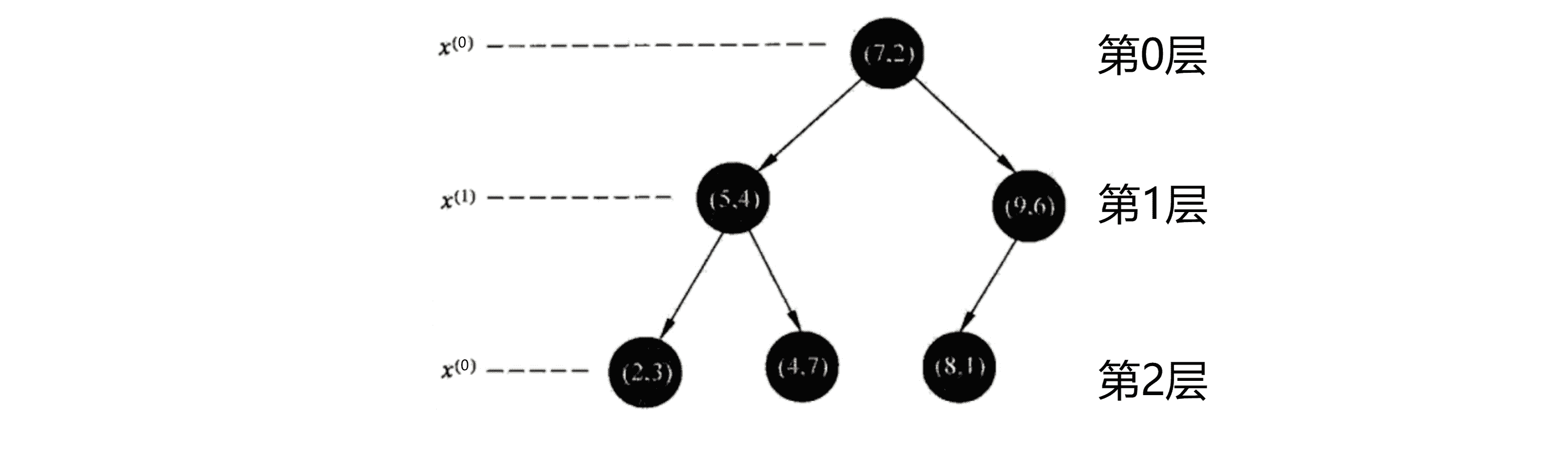
如果你还是感到有些迷茫,没关系,下面我们就一步一步来构建我们的KD树。
第一轮划分,划分的是第 0 层,所以我们这一轮划分 x0 这个维度,本次划分区域为整个平面。我们当前区域的带划分点有(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2),我们将其按照 x0 的大小进行排序得到 (2, 3), (4, 7), (5, 4), (7, 2), (8, 1), (9, 6)。这时的数据集大小k = 6,我们选取 k / 2 + 1 个点即“中位数”点——(7, 2)的作为分界线进行划分,将平面划分为左右两个部分,并将该点加入KD树的二叉树结构中作为根节点:
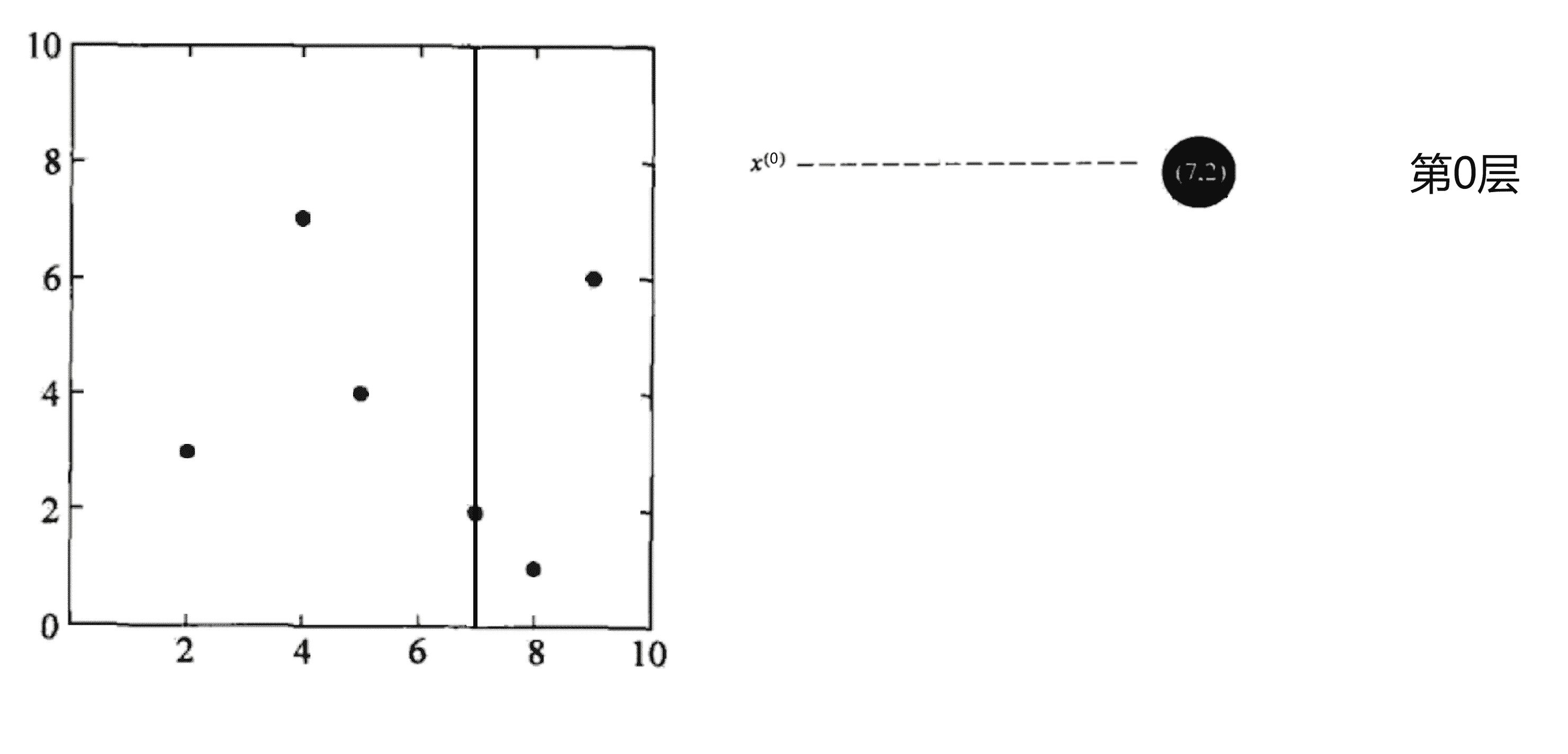
划分完后,左右区域均有未划分节点,我们先划分左区域。
第二轮划分,划分的是第 1 层,所以我们这一轮划分 x1 这个维度,本次划分区域为上次划分的左边区域。我们当前区域的带划分点有(2, 3), (5, 4), (4, 7),我们将其按照 x1 的大小进行排序得到 (2, 3), (5, 4), (4, 7)。这时的数据集大小 k = 3,我们选取 k / 2 + 1 个点即“中位数”点——(5, 4)的作为分界线进行划分,将平面划分为上下两个部分,并将该点加入KD树的二叉树结构中作为根节点的左儿子节点:
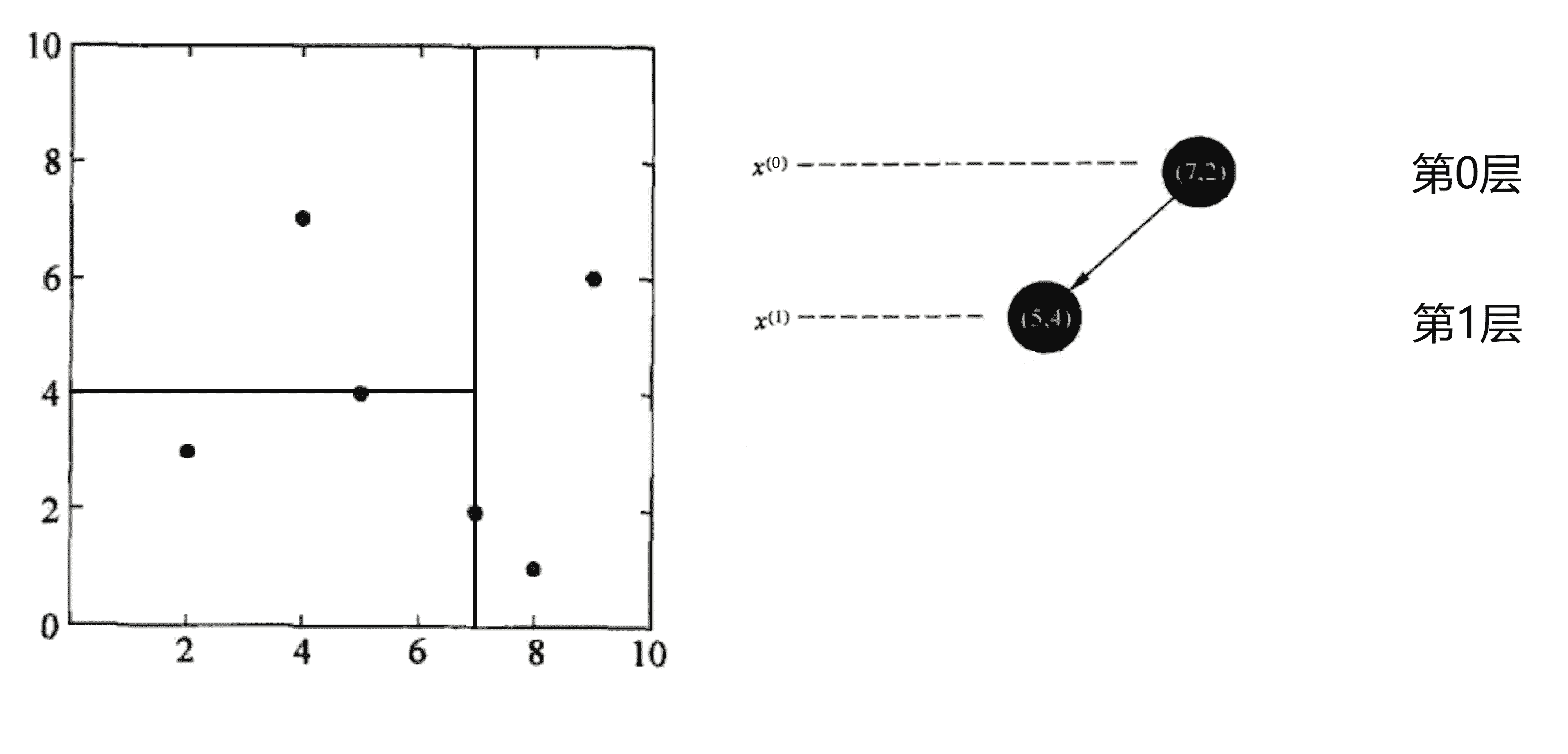
划分完后,上下区域均有未划分节点,我们先划分下区域。
第三轮划分,划分的是第 2 层,所以我们这一轮划分 x0 这个维度,本次划分区域为上次划分的下边区域。我们当前区域的带划分点有(2, 3),我们将其按照 x0 的大小进行排序得到 (2, 3)。这时的数据集大小 k = 1,我们选取 k / 2 + 1 个点即“中位数”点——(2, 3)的作为分界线进行划分,将平面划分为左右两个部分,并将该点加入KD树的二叉树结构中作为第二轮划分的节点的左儿子节点:
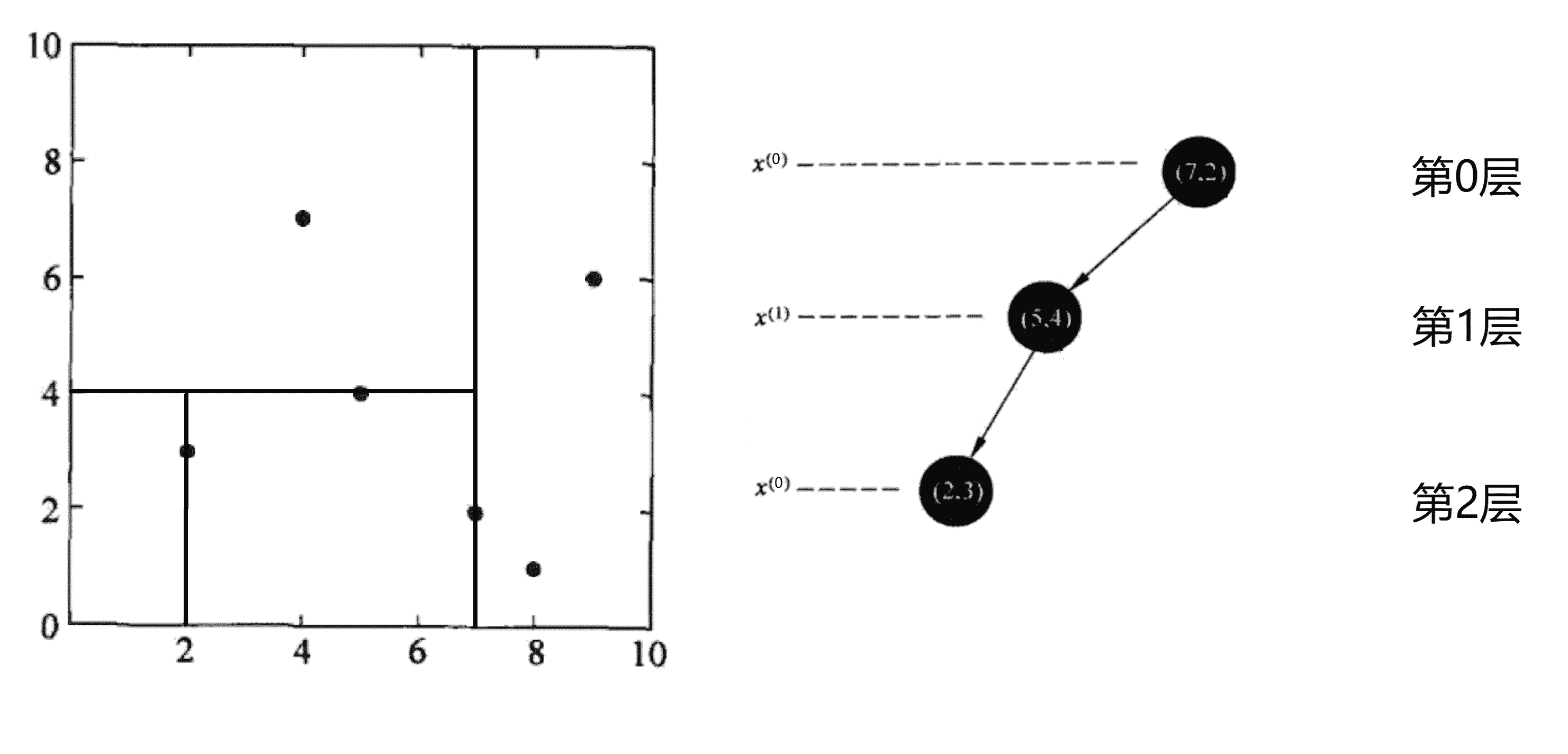
划分完后,左右区域均无未划分节点,直接递归回溯处理第二轮划分产生的上区域。
第四轮划分,划分的是还是第 2 层,所以我们这一轮划分 x0 这个维度,本次划分区域为第二轮划分的上边区域。我们当前区域的带划分点有(4, 7),我们将其按照 x0 的大小进行排序得到 (4, 7)。这时的数据集大小 k = 1,我们选取 k / 2 + 1 个点即“中位数”点——(4, 7)的作为分界线进行划分,将平面划分为左右两个部分,并将该点加入KD树的二叉树结构中作为第二轮划分的节点的右儿子节点:
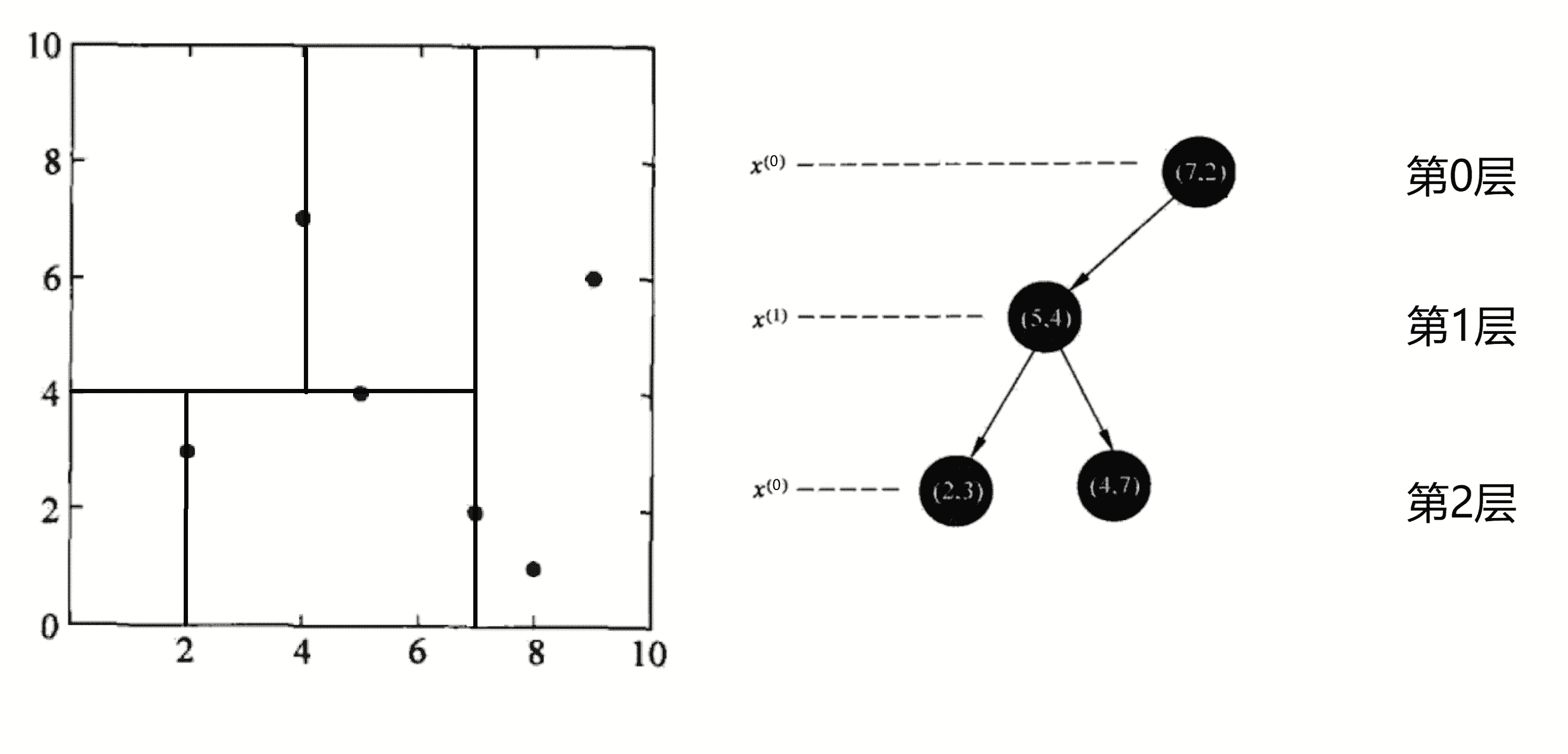
划分完后,左右区域均无未划分节点,回溯发现第二轮的上下划分区域均出力完毕,直接递归回溯处理第一轮划分产生的右区域。
第五轮划分,划分的是第 2 层,所以我们这一轮划分 x1 这个维度,本次划分区域为第一轮划分的右边区域。我们当前区域的带划分点有(8, 1), (9, 6),我们将其按照 x1 的大小进行排序得到 (8, 1), (9, 6)。这时的数据集大小 k = 2,我们选取 k / 2 + 1 个点即“中位数”点——(9, 6)的作为分界线进行划分,将平面划分为上下两个部分,并将该点加入KD树的二叉树结构中作为根节点的右儿子节点:
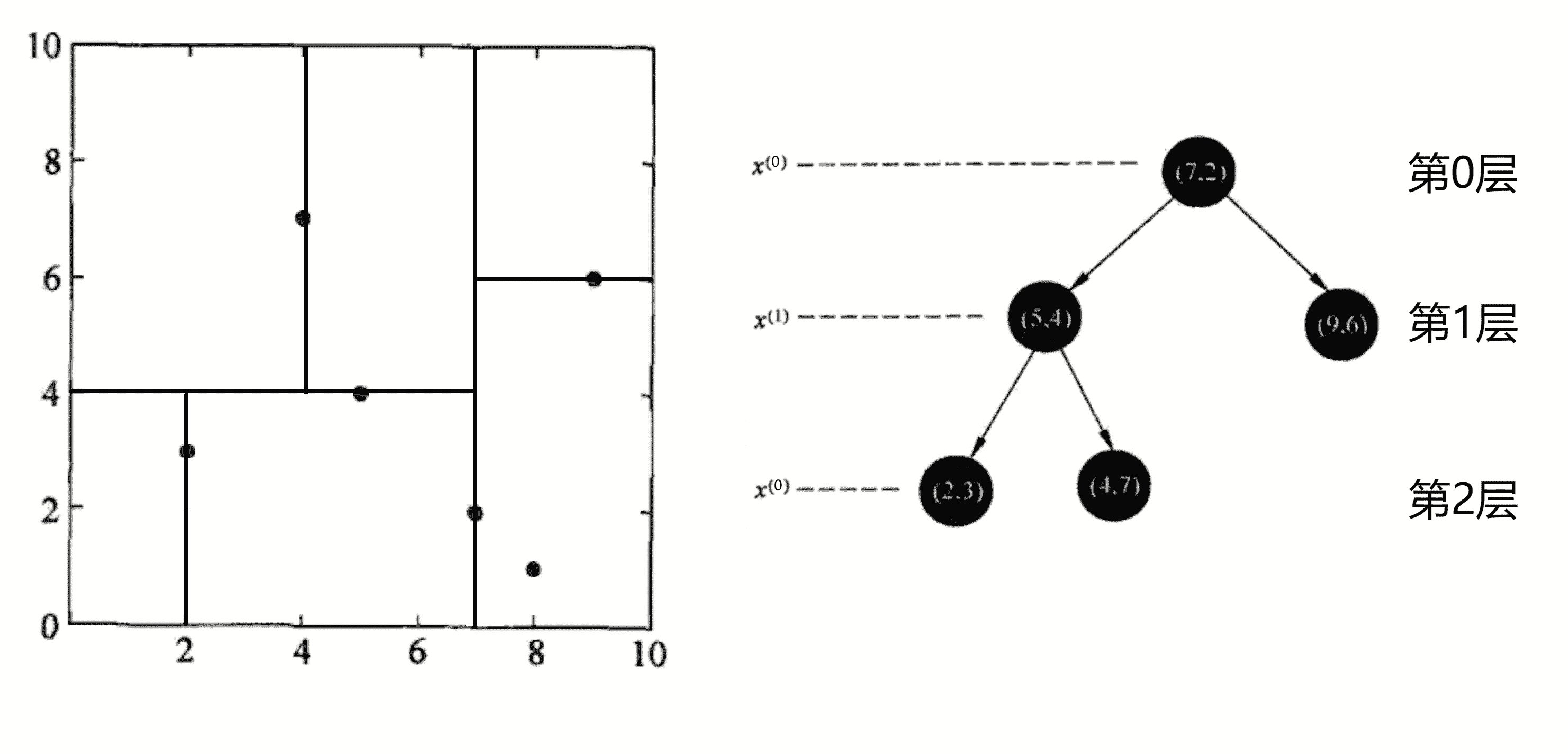
划分完后,只有下区域存在未划分节点,我们直接去划分下区域。
第六轮划分,划分的是第 2 层,所以我们这一轮划分 x0 这个维度,本次划分区域为上次划分的下边区域。我们当前区域的带划分点有(8, 1),我们将其按照 x0 的大小进行排序得到 (8, 1)。这时的数据集大小 k = 1,我们选取 k / 2 + 1 个点即“中位数”点——(8, 1)的作为分界线进行划分,将平面划分为左右两个部分,并将该点加入KD树的二叉树结构中作为第二轮划分的节点的左儿子节点:
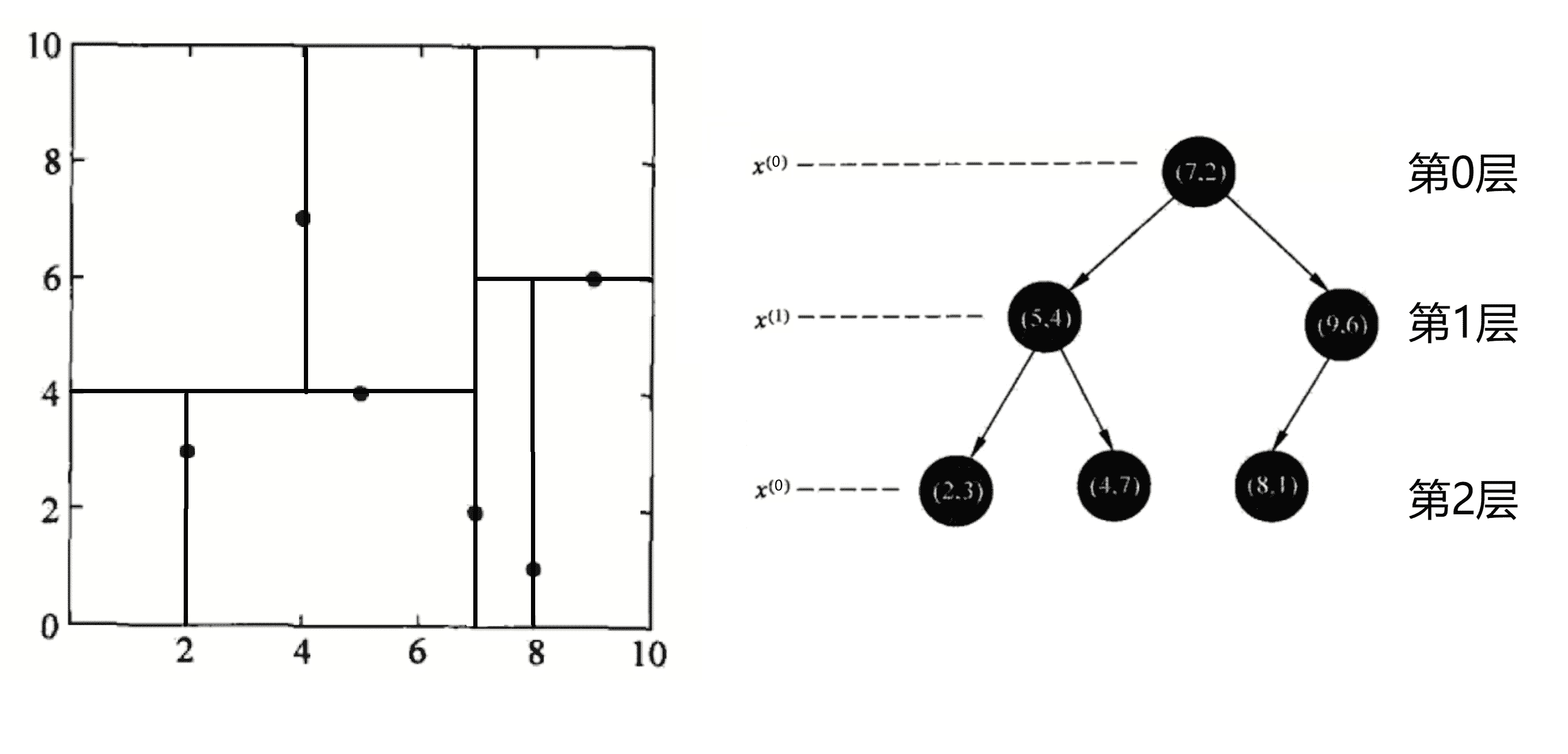
划分完后,我们发现所有节点都已经被划分,我们的KD树也就建立好了。
实现代码
思路已经很明了了,实现代码也呼之欲出了:
void build(int l, int r, int rt = 1, int dep = 0) {
if(l > r) return;//如果没用节点
son[rt] = r - l;//表示还余下多少未划分节点
son[rt * 2] = son[rt * 2 + 1] = -1;//初始值
idx = dep % k;//计算当前层的划分维度
int mid = (l + r + 1) / 2;//计算k(mid)
nth_element(po + l, po + mid, po + r + 1);//查找l到r中在idx维度上第 mid 大的数,并放在po[mid]整个位置上
pt[rt] = po[mid];//当前层KD数节点放po[mid]这个节点
build(l, mid - 1, rt * 2, dep + 1);
build(mid + 1, r, rt * 2 + 1, dep + 1);
//递归构建下一层
return ;
}KD树的查找
实现原理
在建立好KD树之后,假如我们要继续查找攻击力在[al,ar],防御力在[dl,dr]之间的角色数量,我们要怎么做呢?其实非常简单。
我们还是用回之前的例子,假设我们已经运用上面的代码,将(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)建立好了KD树:

接下来我们只需递归判断,若现在递归到的这一层有可能包含攻击力在[al,ar],防御力在[dl,dr]之间的角色,则递归下去,直到当前层只有一个节点且满足条件时ans++;反之,若这一层不可能包含攻击力在[al,ar],防御力在[dl,dr]之间的角色,则直接回溯到上一层。
我们首先读入minn数组和maxx数组,其中minn[i]和maxx[i]分别代表第i维度的下界和上界,并初始化答案ans = 0。
接着我们对于每一次划分,先判断划分前区域是否直接在给定区域内,若是直接加上改区域内的点数并返回上一层;若不是,先判断划分点是否在查询区域内再判断划分的两个部分中有没有可能有点满足条件,若有则递归判断划分后区域即可。
代码实现
代码也相应的非常简单:
void query(point minn, point maxx, point now_minn, point now_maxx, int rt = 1, int dep = 0) {
if(son[rt] == -1) return;
int flag;
flag = 1;
for(int i = 0; i < k; i++) {
if(now_maxx.x[i] > maxx.x[i] || now_minn.x[i] < minn.x[i]) {
flag = 0;
break;
}
}
if(flag) {
ans += son[rt] + 1;
return;
}
//判定当前区域是否满足条件
flag = 1;
for(int i = 0; i < k; i++) {
if(pt[rt].x[i] > maxx.x[i] || pt[rt].x[i] < minn.x[i]) {
flag = 0;
break;
}
}
ans += flag;
//判定当前划分点是否满足条件
int idx = dep % k;//计算当前层的划分维度
if(pt[rt].x[idx] > minn.x[idx]) {
int temp = now_maxx.x[idx];
now_maxx.x[idx] = pt[rt].x[idx];
query(minn, maxx, now_minn, now_maxx, rt * 2, dep + 1);
now_maxx.x[idx] = temp;
}
if(pt[rt].x[idx] < maxx.x[idx]) {
int temp = now_minn.x[idx];
now_minn.x[idx] = pt[rt].x[idx];
query(minn, maxx, now_minn, now_maxx, rt * 2 + 1, dep + 1);
now_minn.x[idx] = pt[rt].x[idx];
}
//分别判断两个划分区域是否与查询区域相交
return ;
}经典例题
[JROJ]蒟蒻联盟
题目描述
假如在一款叫做《蒟蒻联盟》的游戏中,第一行两个整数n和k,代表一共有 n(n≤1e5)个角色,每个角色都有 k(k≤5) 维能力;
接下来 n 行,每行 k 个整数,代表每个角色的k维能力值。
接下来一个整数m,代表有m(m≤1e5)次询问,每次询问给定 n 对整数,第 i 对整数x, y代表所需要的数据第 i 维数据要求落在在[x,y]内,每次询问要求输出满足条件的角色数量。
解题思路
就是我们之前思考的例子,下面见模板:
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 55555, K = 5;
const int inf = 0x3f3f3f3f;
#define sqr(x) (x)*(x)
int k, n, idx, ans = 0; //k为维数,n为点数
struct point {
int x[K];
bool operator < (const point &u) const {
return x[idx] < u.x[idx];
}
}po[N];
typedef pair<double, point>tp;
priority_queue<tp>nq;
struct kdTree {
point pt[N << 2];
int son[N << 2];
void build(int l, int r, int rt = 1, int dep = 0) {
if(l > r) return;//如果没用节点
son[rt] = r - l;//表示还余下多少未划分节点
son[rt * 2] = son[rt * 2 + 1] = -1;//初始值
idx = dep % k;//计算当前层的划分维度
int mid = (l + r + 1) / 2;//计算k(mid)
nth_element(po + l, po + mid, po + r + 1);//查找l到r中在idx维度上第 mid 大的数,并放在po[mid]整个位置上
pt[rt] = po[mid];//当前层KD数节点放po[mid]这个节点
build(l, mid - 1, rt * 2, dep + 1);
build(mid + 1, r, rt * 2 + 1, dep + 1);
//递归构建下一层
return ;
}
void query(point minn, point maxx, point now_minn, point now_maxx, int rt = 1, int dep = 0) {
if(son[rt] == -1) return;
int flag;
flag = 1;
for(int i = 0; i < k; i++) {
if(now_maxx.x[i] > maxx.x[i] || now_minn.x[i] < minn.x[i]) {
flag = 0;
break;
}
}
if(flag) {
ans += son[rt] + 1;
return;
}
//判定当前区域是否满足条件
flag = 1;
for(int i = 0; i < k; i++) {
if(pt[rt].x[i] > maxx.x[i] || pt[rt].x[i] < minn.x[i]) {
flag = 0;
break;
}
}
ans += flag;
//判定当前划分点是否满足条件
int idx = dep % k;//计算当前层的划分维度
if(pt[rt].x[idx] > minn.x[idx]) {
int temp = now_maxx.x[idx];
now_maxx.x[idx] = pt[rt].x[idx];
query(minn, maxx, now_minn, now_maxx, rt * 2, dep + 1);
now_maxx.x[idx] = temp;
}
if(pt[rt].x[idx] < maxx.x[idx]) {
int temp = now_minn.x[idx];
now_minn.x[idx] = pt[rt].x[idx];
query(minn, maxx, now_minn, now_maxx, rt * 2 + 1, dep + 1);
now_minn.x[idx] = pt[rt].x[idx];
}
//分别判断两个划分区域是否与查询区域相交
return ;
}
}kd;
void print(point &p) {
for(int j = 0; j < k; j++) printf("%d%c", p.x[j], j==k-1?'\n':' ');
}
int main() {
scanf("%d%d", &n, &k);
point data_minn, data_maxx;
for(int i = 0; i < n; i++) {
for(int j = 0; j < k; j++) {
scanf("%d",&po[i].x[j]);
if(i == 0) data_minn.x[j] = data_maxx.x[j] = po[i].x[j];
else {
data_minn.x[j] = min(data_minn.x[j], po[i].x[j]);
data_maxx.x[j] = max(data_maxx.x[j], po[i].x[j]);
}
}
//计算初始范围
}
kd.build(0, n - 1);
int t, m;
for(scanf("%d", &t); t--;) {
point minn, maxx;//下界和上界
point now_minn = data_minn, now_maxx = data_maxx;//初始化当前区域的下界和上界
for(int j = 0; j < k; j++) scanf("%d%d", &minn.x[j], &maxx.x[j]);//设定初始区域
ans = 0;//初始化答案为0
kd.query(minn, maxx, now_minn, now_maxx);
printf("the number is:%d\n", ans);
}
return 0;
}K邻近问题的应用
KD树不仅能够求取某个多维范围内的数据点个数,还能解决经典的K邻近问题(KNN)。
什么是K邻近问题
所谓K邻近问题,就是在 k 维度空间中先给定 n 个样本点,接着 m 次询问,每次给你一个点 (x0, x1 …… xk - 1),要求输出离它最近的 K 个样本点(注意k和K的区别)。
这种问题,放在之前,我们只能暴力枚举每个点计算其与询问点的距离,再用优先队列之类的数据结构来维护前K小的距离点,这样时间复杂度就来到了O(nmklogK)。那使用KD树我们能如何优化算法呢?
KD树
我们还是使用前面《蒟蒻联盟》的例子进行讲解。我们的数据为(2, 3), (5, 4), (9, 6), (4, 7), (8, 1), (7, 2)。
KD树的建立
KD树的建立和之前一模一样,这里就不赘述了,我们直接得到建立好的KD树:

K邻近的查询
实现原理
其实K邻近的查询也很简单,和之前的区域查询类似,我们要去访问所有有可能的区域进行查询。
接下来我们通过网上流传很广的两个例子进行讲解KD树如何求解K邻近问题。为了方便说明,下面我们取K=1,即以最近邻近点问题进行说明。
我们首先以查询(2.1, 3.1)为例:
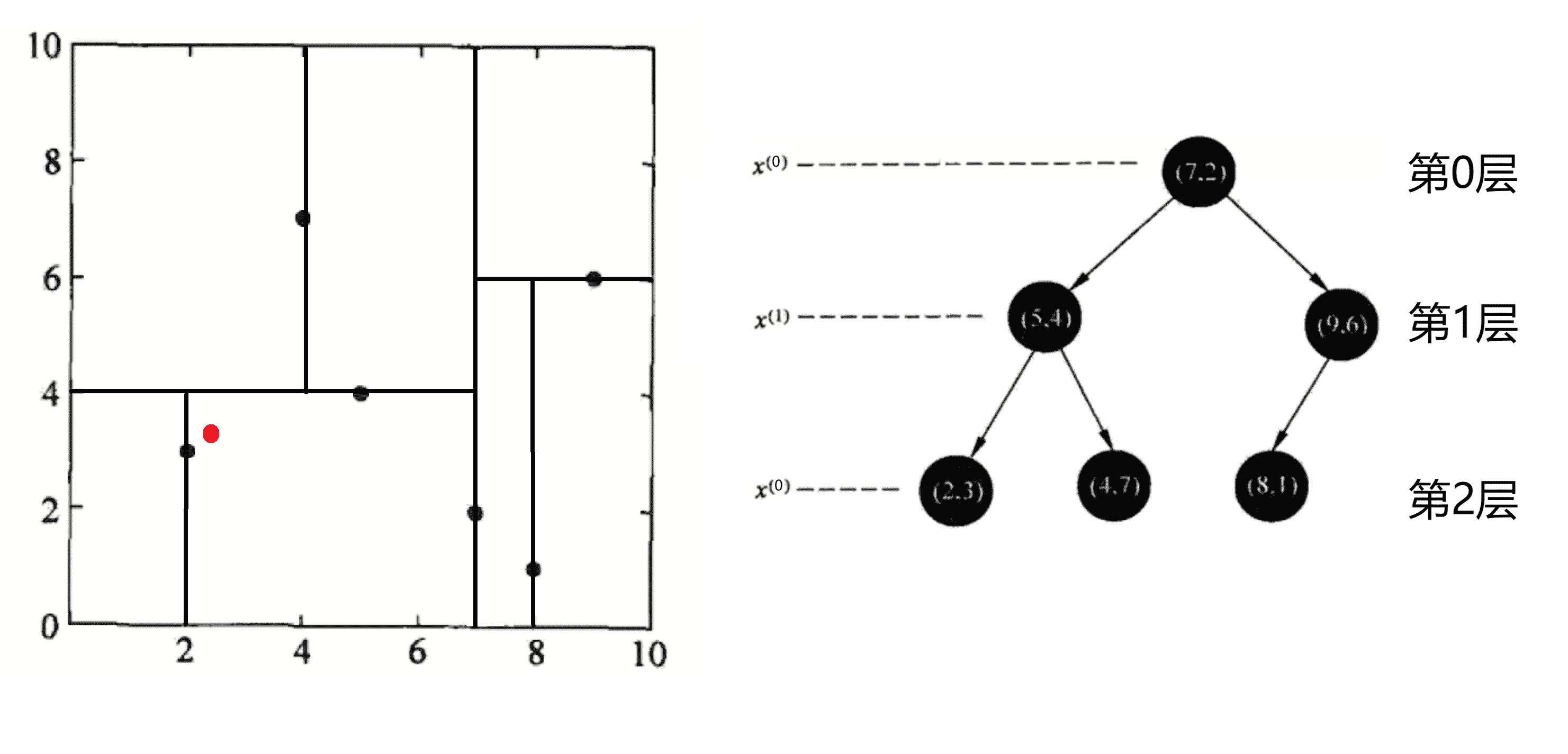
我们的查询分为两步:
1.递归。我们先从根节点(7, 2)点开始递归查找,找到我们查询点(2.1, 3.1)所属区域。我们途径的节点有<(7,2),(5,4),(2,3)>。然后我们比较途径节点与查询点(2.1, 3.1)的距离,取最短的作为当前答案并且做圆:
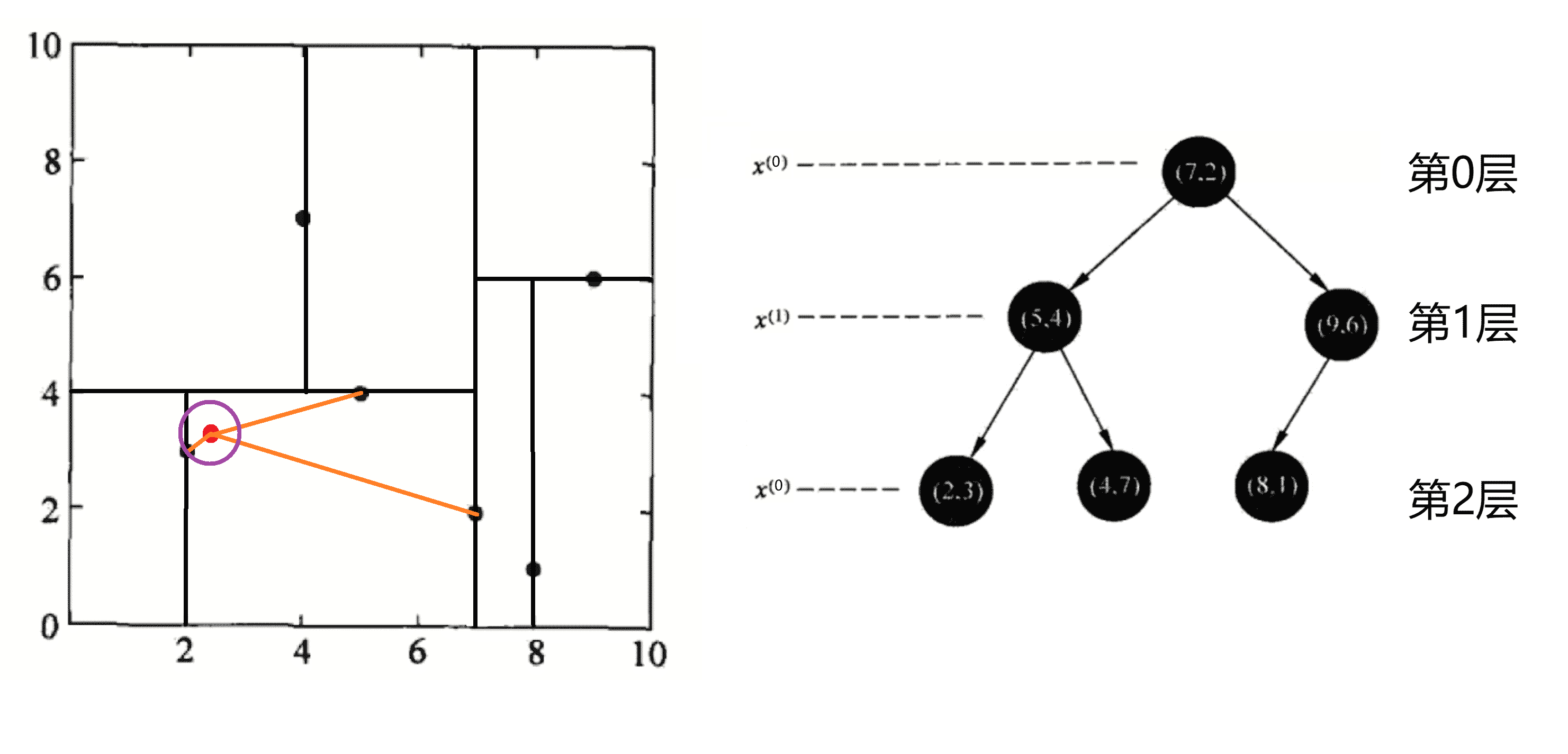
此时以(2,3)作为当前最近邻点,计算其到查询点(2.1,3.1)的距离为0.1414。
2.回溯。我们开始回溯,得到(2,3)为查询点的最近点之后,我们发现(2, 3)已经是叶子节点,所以我们首先回溯到其父节点(5,4),并判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。即我们判断我们的圆是否和当前层切割超平面y = 4相交,很显然不相交因此不用进入(5,4)节点分割的上方空间中(图中蓝色区域)去搜索;
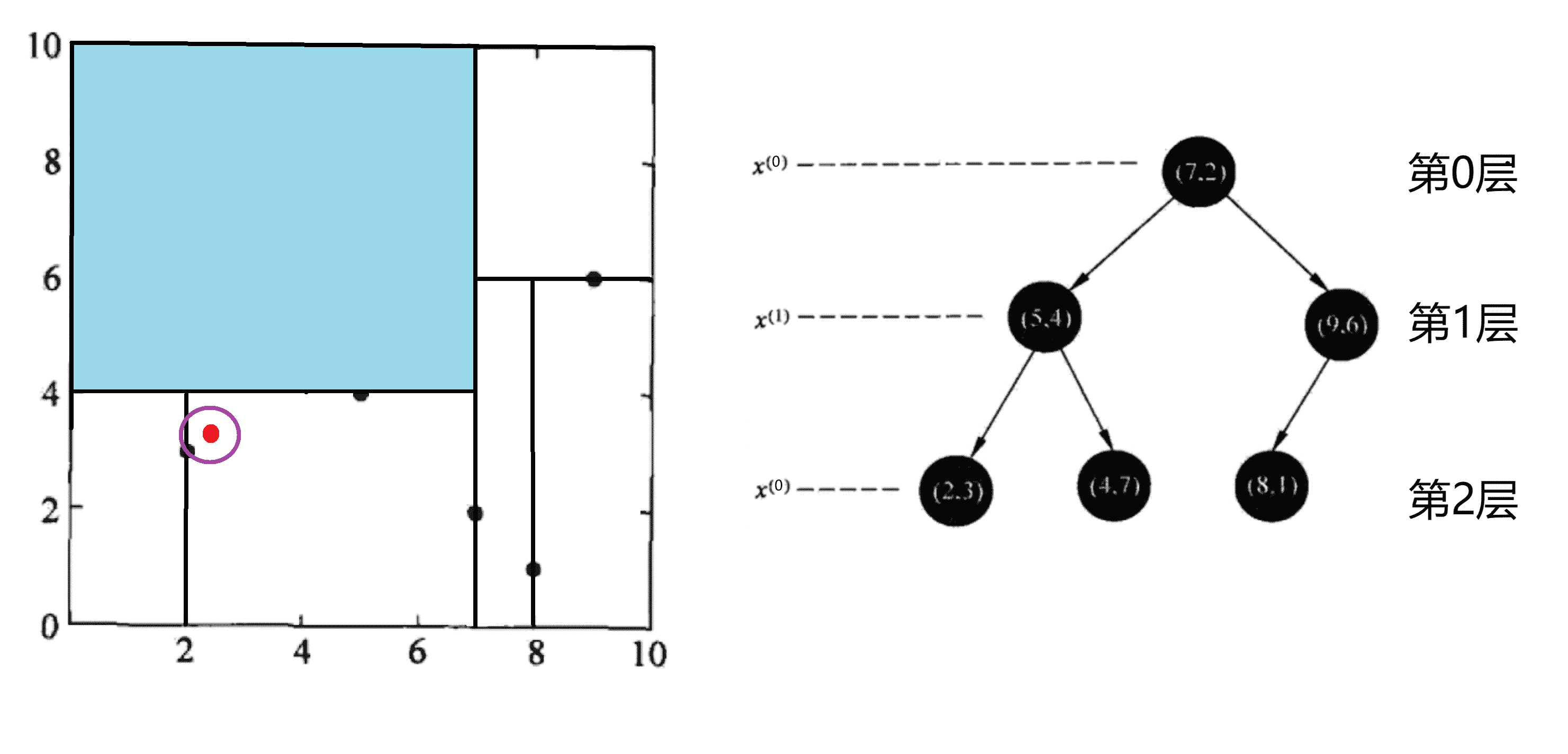
我们继续回溯,回溯到(7,2),我们发现以(2.1,3.1)为圆心,以0.1414为半径的圆更不会与x = 7超平面相交,因此不用进入(7,2)右子空间进行查找(图中蓝色区域)。至此,搜索路径中的节点已经全部回溯完,结束整个搜索,返回最近邻点(2,3),最近距离为0.1414:
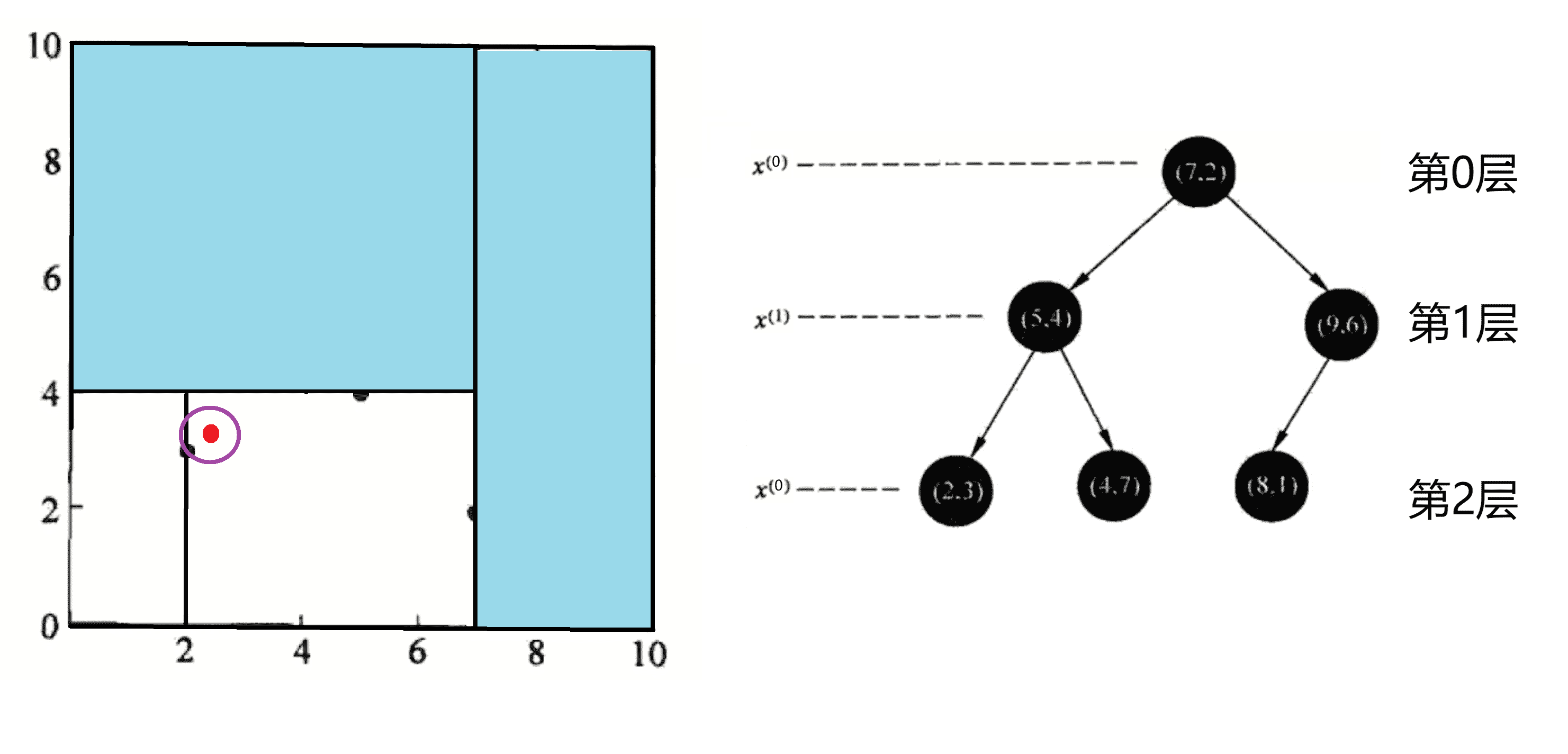
我们再举一个例子,我们这次以查询(2, 4.5)为例:
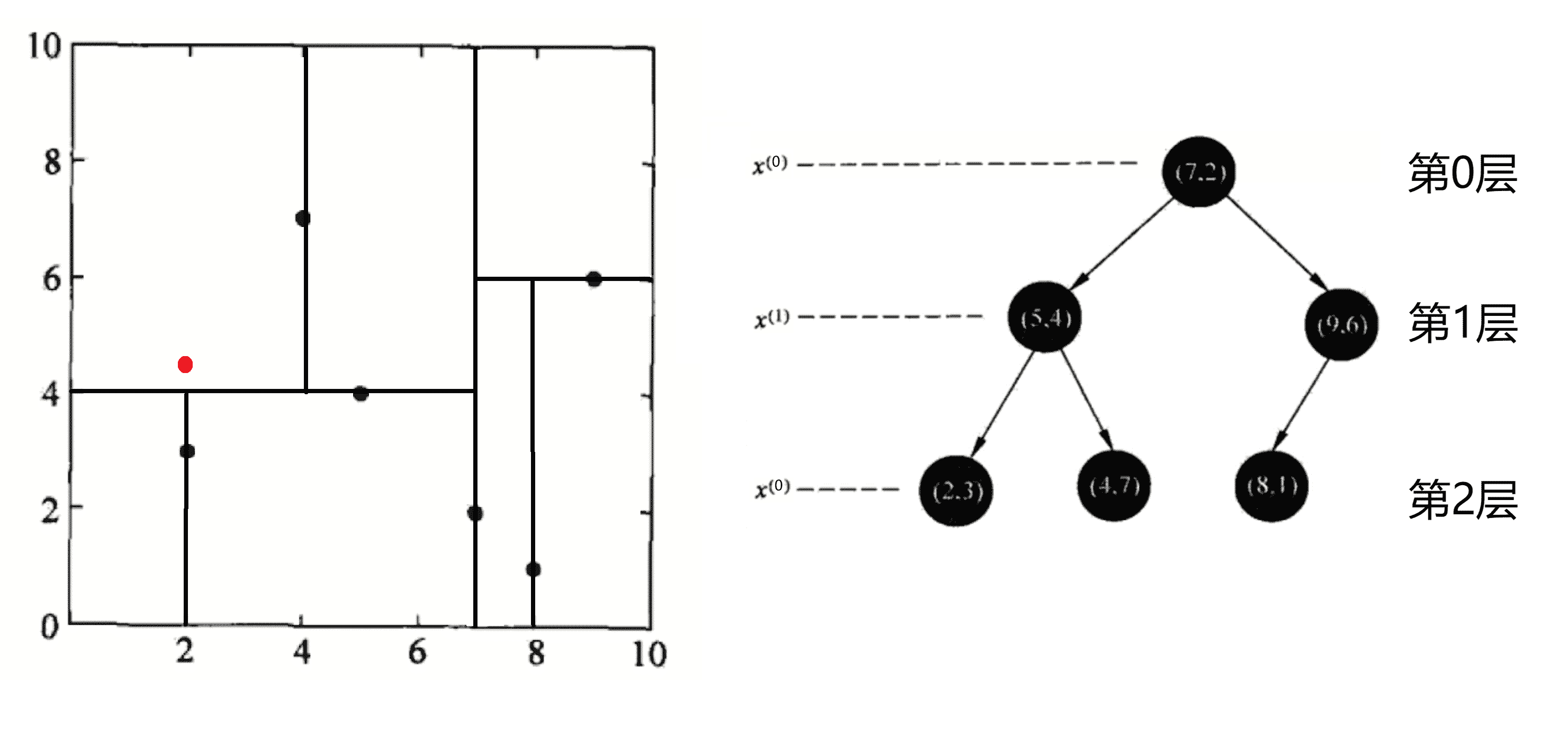
同样地,我们的查询分为两步:
1.递归。我们先从根节点(7, 2)点开始递归查找,找到我们查询点(2, 4.5)所属区域。我们途径的节点有<(7,2),(5,4),(4,7)>。然后我们比较途径节点与查询点(2, 4.5)的距离,取最短的作为当前答案并且做圆:
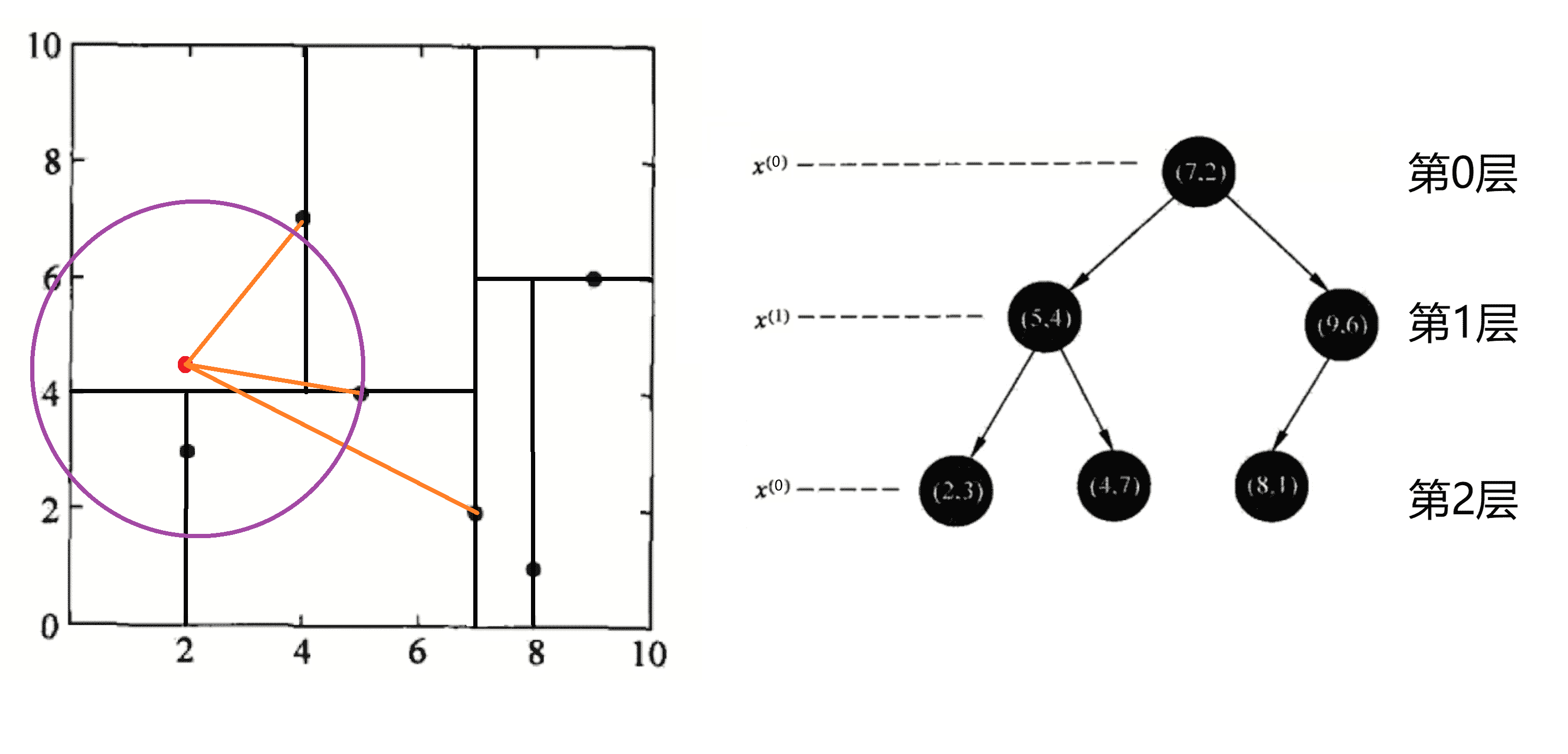
此时以(5,4)作为当前最近邻点,计算其到查询点(2, 4.5)的距离为3.041。
2.回溯。我们开始回溯,得到(2,4.5)为查询点的最近点之后,我们首先回溯到其父节点(5,4),并判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。即我们判断我们的圆是否和当前层切割超平面y = 4相交,这次该圆和y = 4超平面交割,所以需要进入(5,4)分割的下方子空间进行查找,也就是将(2,3)节点加入搜索路径中,这时(2,3)叶子节点,且其距离(2,4.5)比(5,4)要近,所以最近邻点更新为(2,3),最近距离更新为1.5:
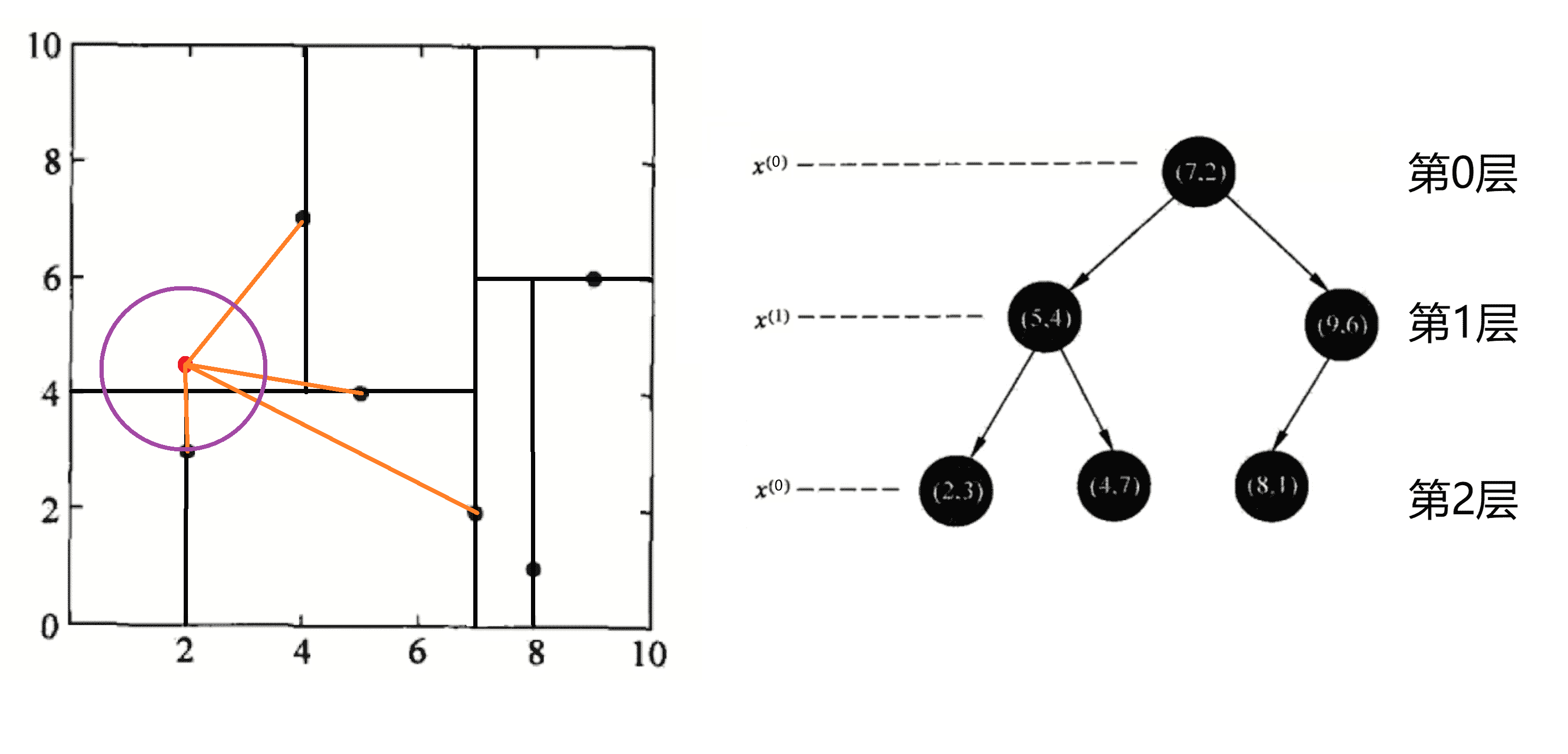
我们继续回溯,回溯到回溯到根结点(7,2)的时候,这时显然以(2,4.5)为圆心1.5为半径作圆,并不和x = 7分割超平面交割,如上图所示。至此,搜索路径回溯完,返回最近邻点(2,3),最近距离1.5。
这就是最邻近点的搜索过程,相信你已经很清楚了。那K邻近点呢?其实是一样的,我们只要以第K邻近点为半径做圆,进行如上过程即可(上述过程即K=1),而维护前K近的点用优先队列就可以啦。
代码实现
原理相信你已经很清楚了,下面来看看这部分的代码吧:
void query(point p, int m, int rt = 1, int dep = 0) {
if(son[rt] == -1) return;//如果该区域没有点
tp nd(0, pt[rt]);//生成pair类型
for(int i = 0; i < k; i++) nd.first += sqr(nd.second.x[i] - p.x[i]);//计算距离
int dim = dep % k, x = rt * 2, y = rt * 2 + 1, fg = 0;
//dim为当前划分维度,x,y为左右儿子节点编号,fg为判断是否进入另一区域
if(p.x[dim] >= pt[rt].x[dim]) swap(x, y);
//如果查询点位于当前划分点的右子树,我们就先访问右儿子
if(~son[x]) query(p, m, x, dep + 1);//如果存在
if(nq.size() < m) nq.push(nd), fg = 1;//如果不够K个点,就加入分化点
else {
if(nd.first < nq.top().first) nq.pop(), nq.push(nd);
//如果分化点到询问点距离小于当前的第K邻近点
if(sqr(p.x[dim] - pt[rt].x[dim]) < nq.top().first) fg = 1;
//如果圆和分化边界相交
}
if(~son[y] && fg) query(p, m, y, dep + 1);
//如果另一区域存在且可能存在更优的邻近点
}经典例题
[HDU 4347]The Closest M Points
题目描述
Problem Description:
The course of Software Design and Development Practice is objectionable. ZLC is facing a serious problem .There are many points in K-dimensional space .Given a point. ZLC need to find out the closest m points. Euclidean distance is used as the distance metric between two points. The Euclidean distance between points p and q is the length of the line segment connecting them.In Cartesian coordinates, if p = (p1, p2,..., pn) and q = (q1, q2,..., qn) are two points in Euclidean n-space, then the distance from p to q, or from q to p is given by:
Can you help him solve this problem?
Input
In the first line of the text file .there are two non-negative integers n and K. They denote respectively: the number of points, 1 <= n <= 50000, and the number of Dimensions,1 <= K <= 5. In each of the following n lines there is written k integers, representing the coordinates of a point. This followed by a line with one positive integer t, representing the number of queries,1 <= t <=10000.each query contains two lines. The k integers in the first line represent the given point. In the second line, there is one integer m, the number of closest points you should find,1 <= m <=10. The absolute value of all the coordinates will not be more than 10000.
There are multiple test cases. Process to end of file.
Output
For each query, output m+1 lines:
The first line saying :”the closest m points are:” where m is the number of the points.
The following m lines representing m points ,in accordance with the order from near to far
It is guaranteed that the answer can only be formed in one ways. The distances from the given point to all the nearest m+1 points are different. That means input like this:
2 2
1 1
3 3
1
2 2
1
will not exist.
Sample Input
3 2
1 1
1 3
3 4
2
2 3
2
2 3
1Sample Output
the closest 2 points are:
1 3
3 4
the closest 1 points are:
1 3
解题思路
题意:KD树模板题。
思路:M近邻和最近邻其实是一样的。M近邻只需要多个优先队列就行了。先一路递归到叶子节点,然后维护优先队列M个节点就OK。下面给出代码模板:
#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 55555, K = 5;
const int inf = 0x3f3f3f3f;
#define sqr(x) (x)*(x)
int k, n, idx; //k为维数,n为点数
struct point {
int x[K];
bool operator < (const point &u) const {
return x[idx] < u.x[idx];
}
}po[N];
typedef pair<double, point>tp;
priority_queue<tp>nq;
struct kdTree {
point pt[N << 2];
int son[N << 2];
void build(int l, int r, int rt = 1, int dep = 0) {
if(l > r) return;//如果没用节点
son[rt] = r - l;//表示还余下多少未划分节点
son[rt * 2] = son[rt * 2 + 1] = -1;//初始值
idx = dep % k;//计算当前层的划分维度
int mid = (l + r + 1) / 2;//计算k(mid)
nth_element(po + l, po + mid, po + r + 1);//查找l到r中在idx维度上第 mid 大的数,并放在po[mid]整个位置上
pt[rt] = po[mid];//当前层KD数节点放po[mid]这个节点
build(l, mid - 1, rt * 2, dep + 1);
build(mid + 1, r, rt * 2 + 1, dep + 1);
//递归构建下一层
return ;
}
void query(point p, int m, int rt = 1, int dep = 0) {
if(son[rt] == -1) return;//如果该区域没有点
tp nd(0, pt[rt]);//生成pair类型
for(int i = 0; i < k; i++) nd.first += sqr(nd.second.x[i] - p.x[i]);//计算距离
int dim = dep % k, x = rt * 2, y = rt * 2 + 1, fg = 0;
//dim为当前划分维度,x,y为左右儿子节点编号,fg为判断是否进入另一区域
if(p.x[dim] >= pt[rt].x[dim]) swap(x, y);
//如果查询点位于当前划分点的右子树,我们就先访问右儿子
if(~son[x]) query(p, m, x, dep + 1);//如果存在
if(nq.size() < m) nq.push(nd), fg = 1;//如果不够K个点,就加入分化点
else {
if(nd.first < nq.top().first) nq.pop(), nq.push(nd);
//如果分化点到询问点距离小于当前的第K邻近点
if(sqr(p.x[dim] - pt[rt].x[dim]) < nq.top().first) fg = 1;
//如果圆和分化边界相交
}
if(~son[y] && fg) query(p, m, y, dep + 1);
//如果另一区域存在且可能存在更优的邻近点
}
}kd;
void print(point &p) {
for(int j = 0; j < k; j++) printf("%d%c", p.x[j], j==k-1?'\n':' ');
}
int main() {
while(scanf("%d%d",&n, &k) != EOF) {
for(int i = 0; i < n; i++) {
for(int j = 0; j < k; j++) scanf("%d",&po[i].x[j]);
}
kd.build(0, n - 1);
int t, m;
for(scanf("%d", &t); t--;) {
point ask;
for(int j = 0; j < k; j++) scanf("%d", &ask.x[j]);
scanf("%d", &m); kd.query(ask, m);
printf("the closest %d points are:\n", m);
point pt[20];
for(int j = 0; !nq.empty(); j++) pt[j] = nq.top().second, nq.pop();
for(int j = m - 1; j >= 0; j--) print(pt[j]);
}
}
return 0;
}结语
在最后的最后,我们再来看看KD树的时间复杂度吧。我们知道KD树在二维情况下的时间复杂度递推式如下:
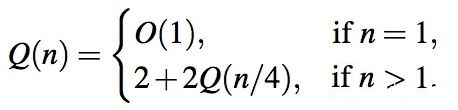
我们就知道如此一来,由主定理就得到在二维下KD树做range-query的时间复杂度为O(sqrt(n)+k)。同理在K维下的时间复杂度就为时间复杂度为O(n^((k-1)/k)+m)。
我们这篇BLOG讲了这么多KD树的妙用之处,那KD树有局限性吗?当然是有的,受限于结构,KD树一般是静态的,若要实现动态KD树,结构的破坏其时间复杂度就会变大,但仍然有更加高级的其他算法能够解决动态的问题。
这就是KD树的全部,最后希望你喜欢这篇BLOG(偷偷庆祝一下蒟蒻的第100篇BLOG)!
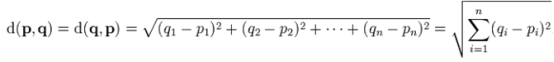
对于2D的查找,有一个数据结构叫2D range tree, 最快能以O(logn +k)的时间复杂度查找。
请问大佬,有什么更高级的算法能够解决动态问题呢
感谢OωO