咳咳，上次写完凸包后，Blog就由于服务器的原因炸了两天:sob:这两天我试着研究了一下半平面交，发现其实和高中数学的“线性规划”有着很大的关系（什么你不会，问题不大），这篇博客就让你彻底学会求半平面交的面积。

写在前面

在这篇BLOG中，为了方便讲解我们默认把一条有向直线的左侧设为该半平面的有效区域。:smirk:

什么是半平面

大家都知道形如ax+by+c=0的图形称为直线。那么半平面就是形如ax+by+c>0(或小于零)所代表的区域。如图，在这幅图中，ax+by+c>0这个不等式代表的区域就是这条直线的上方。等价的，如果规定这条直线的方向为P1点指向P2点，那么这个半平面的区域就是P1P2的左侧。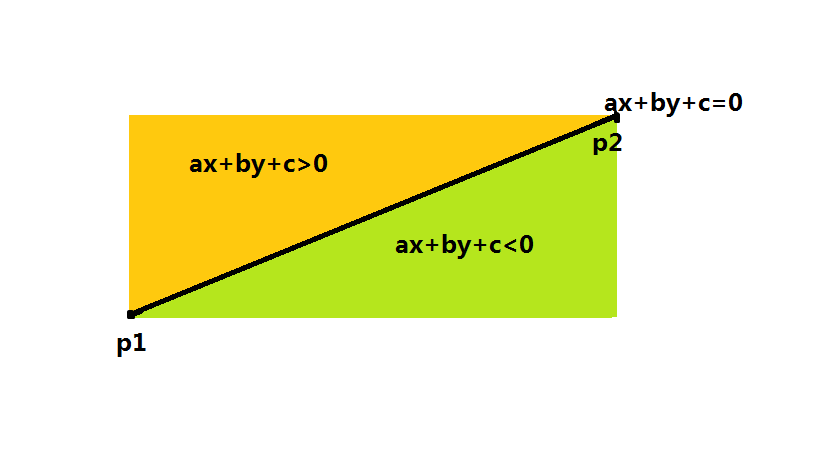

什么是半平面交

多个半平面同时覆盖到的区域称为半平面交。比如我们定义直线的左侧是半平面的有效区域，那么图中的红色区域就是三条直线的半平面交，而题目就是要我们计算这个半平面交的面积。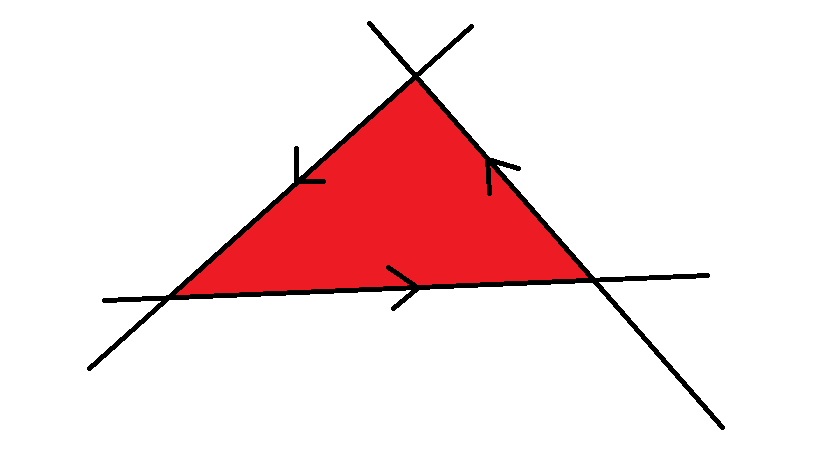

怎么解决半平面交面积问题

别急，我会把程序分块，一块一块进行讲解。

定义点和线

因为会涉及到两条直线的交点的计算，即使题目给出的坐标都为整数，这里还是要用double，定义点代码如下：

struct point
{
    double x,y;
}plist[Maxn];int pl;

接下来是定义一条边，两点确定一条直线，所以需要两个点p1，p2；这次我们在边里面多了一个参数angle，这是用来计算这条有向直线的角度的，而内部的segment则是为了方便读取一条直线，是不是很简单啊，代码如下：

struct segment
{
    point p1,p2;//两个点
    double angle;//该直线斜率
    segment(){}//读取坐标
    segment(double x1,double y1,double x2,double y2)
    {
        p1.x=x1;p1.y=y1;
        p2.x=x2;p2.y=y2;
    } 

    void get_angle()
    {
        angle=atan2(p2.y-p1.y,p2.x-p1.x);
    }//计算斜率
}seg[Maxn],sglist[Maxn];int head,tail;

叉积

大家都见过很多次了，就不再介绍了，直接贴代码：

double multi(point p1,point p2,point p0)
{
    double x1=p1.x-p0.x;
    double y1=p1.y-p0.y;
    double x2=p2.x-p0.x;
    double y2=p2.y-p0.y;
    return(x1*y2-x2*y1);
}

计算两条直线的交点

这里我们提供了两种写法，一种好理解，一种好记忆，就看你自己选择吧，现在我们逐一讲解。

好理解的版本

通过两个点(x1,y1)、(x2,y2)，我们可以用x1，x2，y1，y2表示这条直线的方程ax+by+c=0，然后通过两条直线的方程，我们可以用a1，a2，b1，b2，c1，c2表示出他们的交点，这就是这段代码的思路：

point jd(segment sg1,segment sg2)
{
    point p1,p2,p3,p4,ret;
    p1=sg1.p1;p2=sg1.p2;
    p3=sg2.p1;p4-sg2.p2;

    double a1,a2,b1,b2,c1,c2;

    a1=p1.y-p2.y;
    b1=p2.x-p1.x;
    c1=p1.x*p2.y-p2.x*p1.y;
    //计算出第一条直线的方程 

    a2=p3.y-p4.y;
    b2=p4.x-p3.x;
    c2=p3.x*p4.y-p4.x*p3.y;
    //计算出第二条直线的方程 

    ret.x=(c1*b2-c2*b1)/(a2*b1-a1*b2);
    ret.y=(c2*a1-c1*a2)/(a2*b1-a1*b2);
    //计算出交点 
    return ret;
}

好记忆的版本

上面那段代码虽然非常容易想到，但是在赛场上如果用大量时间去推导公式就有些得不偿失。所以，这里给出一种使用叉积的简单的方法，由于原理十分复杂，就不在这里证明了，大体思路是用叉积替代刚刚的直线求交点，有兴趣可以自己去证明一下，下面贴出代码：

point jd(segment sg1,segment sg2)
{
    point p,p1=sg1.p1,p2=sg1.p2,p3=sg2.p1,p4=sg2.p2;
    double t1=multi(p1,p4,p3);
    double t2=multi(p2,p4,p3);

    p.x=(t1*p2.x-t2*p1.x)/(t1-t2);
    p.y=(t1*p2.y-t2*p1.y)/(t1-t2);

    return(p);
}

判断一个点与直线的关系

由于在计算中，我们经常要涉及到一个点在一条有向直线的左边还是右边，这时我们可以用叉积来进行判断，代码如下：

bool satisfy(point p,segment sg)
//点在有向直线的左侧或者在直线上为true
//反之如果点在有向直线的右侧上则为false
{
    if(multi(p,sg.p2,sg.p1)<=eps)return true;
    else return false;
}

用下面这幅图能很好的解释这个算法的原理：

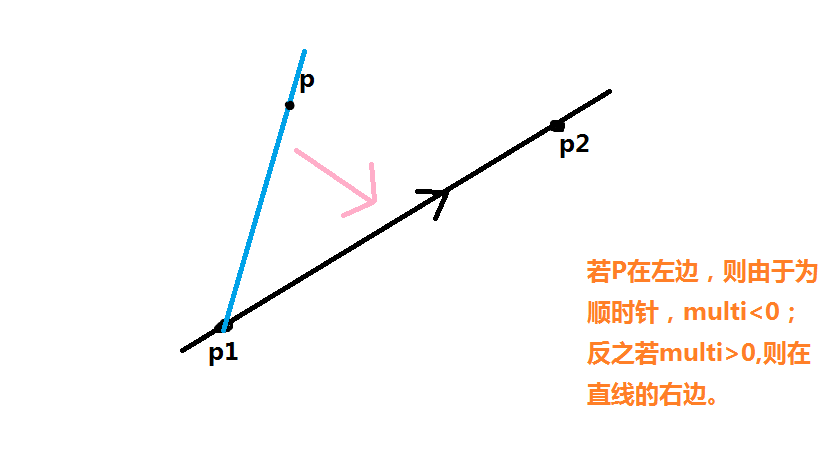
对了，这里还要介绍一下eps是什么？由于是实数计算，所以存在很小很小的误差（比如原本应该为0，单可能计算到0.000000000001），但还是会导致一定的偏差。所以在程序开头，我们就已经定义好了偏差值，防止造成数据判断上的偏差：

#define eps 1e-8

对于边的处理

我们只需在主程序中依次读取每一条边，顺便再计算出每一条有向直线的斜率即可，非常简便：

    scanf("%d",&n);
    double x1,x2,y1,y2;
    for(int i=1;i<=n;i++)
    {
        scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
        seg[i+4]=segment(x1,y1,x2,y2);
        seg[i+4].get_angle();
    }

*对于半平面交的处理

这就是整段代码中最难懂的部分了(其实也不是太难)。
首先为了方便后面的处理，我们要先对直线进行排序，排序的顺序是角度小的放在前面，角度相同时则把靠左边的放在前面，代码如下：

bool cmp(segment sg1,segment sg2)
{
    if( sg1.angle<sg2.angle )return(true);
    if( fabs(sg1.angle-sg2.angle)<eps && satisfy(sg1.p1,sg2)==true)return(true);
    return(false);
}

排序完成后，我们再对直线进行一次筛选，因为如果两条直线平行，那么如图，靠右边的区域一定覆盖了靠左边的区域，又由于是求半平面的交集，所以右边的直线可以直接删去留下左边的直线。

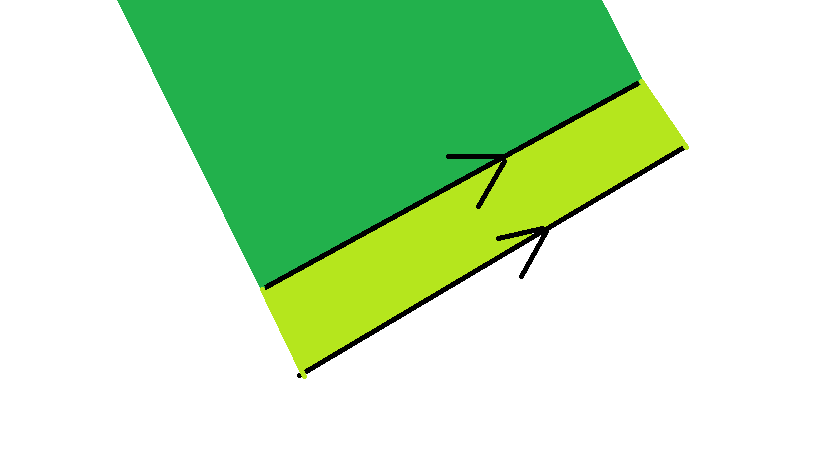
具体代码如下：

    int tp=1;
    for(int i=2;i<=n;i++)if(seg[i].angle-seg[tp].angle> eps )seg[++tp]=seg[i];
    n=tp;

接着我们先加入最开始的两条直线，然后逐一加入直线。但在加入直线前，都要把加入直线后对答案没有贡献了的直线删除掉。这是什么意思呢？

比如我们先加入了seg1，seg2，seg3三条有向直线；

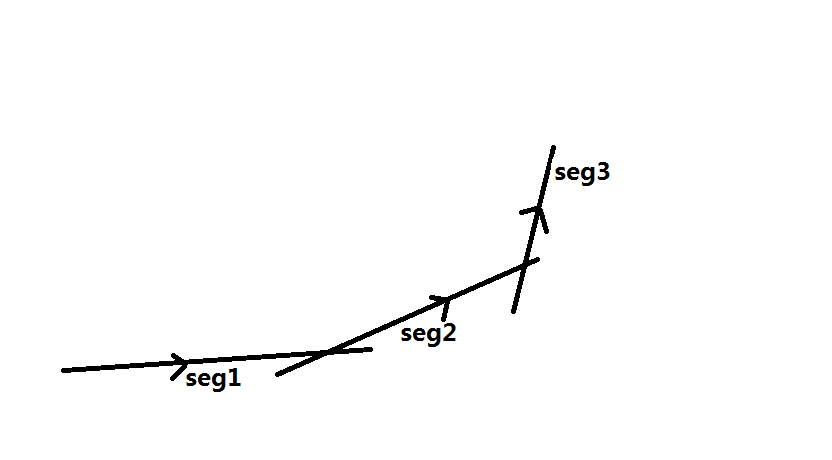
按照角度，这时候我们加入seg4，然后我们发现由于seg4在seg3的左边，角度还比seg3大，seg4贡献的区域包含在seg3对答案贡献的区域，所以seg3没有用了，这时候队尾tail--，seg3出队。

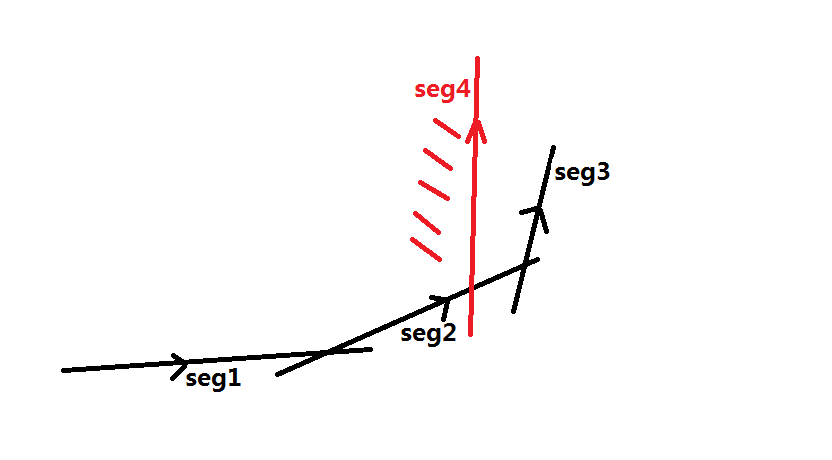
通过总结我们发现，当队尾两条直线的交点在新加入直线的右侧时，最后一条直线对答案无贡献，此时我们tail--，去掉队尾最后一条直线。

同理对于对头，加入我们加入了seg1，seg2，seg3，seg4四条有向直线；

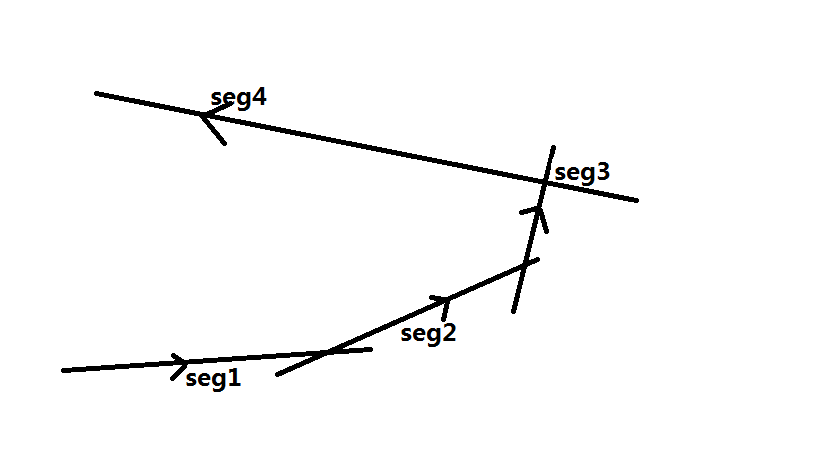
这时按照角度加入seg5，我们发现，出现了和刚刚类似的情况，seg5在seg1和seg2交点的左边（因为直线有向），此时seg5对答案贡献的半平面完全包含于seg1贡献的半平面，所以seg1对答案已经毫无作用了，因此对头指针head++，相当于删除了seg1；

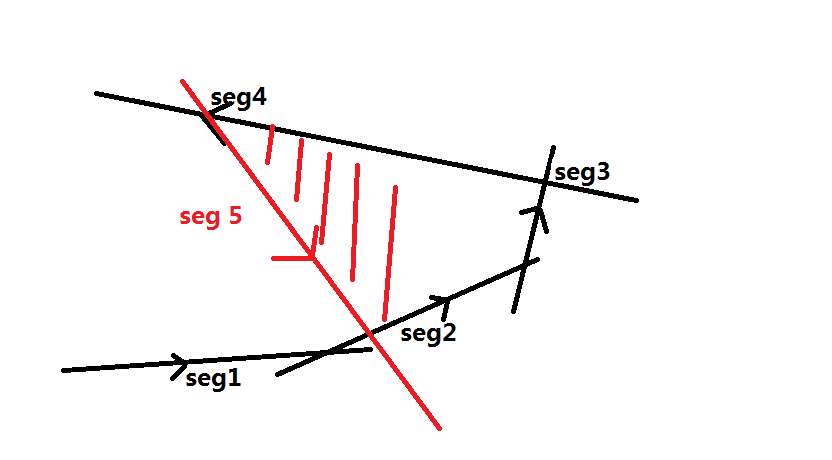
操作结束后还要用队首元素去判断是否删除队尾元素，用队尾元素去判断是否删去队首元素。这又是为什么呢？请看下图：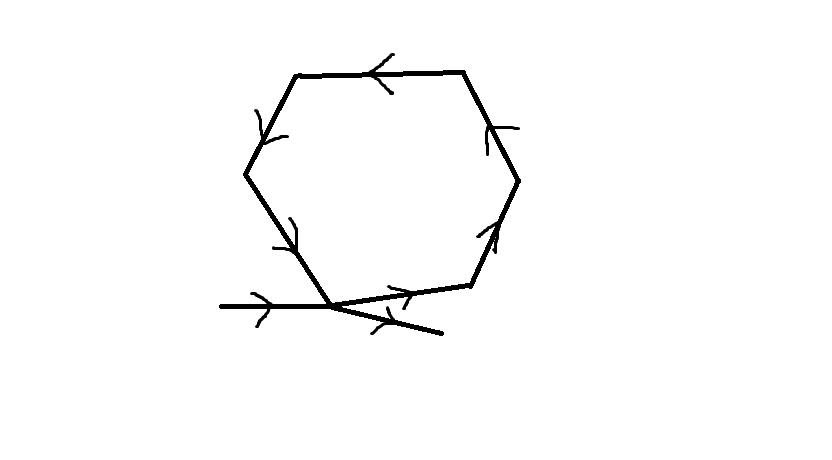
操作完成后，可能会出现这种情况，队首和队尾对答案都没有贡献，这样用队首元素去判断是否删除队尾元素，用队尾元素去判断是否删去队首元素后，就会形成一个完整的圈。

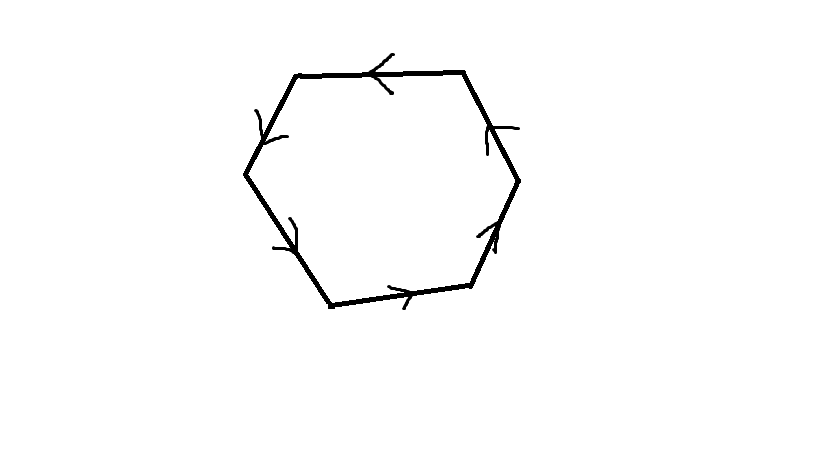
具体代码如下：

sglist[1]=seg[1];sglist[2]=seg[2];
    head=1;tail=2;
    for(int i=3;i<=n;i++)
    {
        while(head<tail && satisfy( jd(sglist[tail] , sglist[tail-1]) , seg[i])==false )tail--;
        while(head<tail && satisfy( jd(sglist[head] , sglist[head+1]) , seg[i])==false )head++;
        sglist[++tail]=seg[i];
    }

    while(head<tail && satisfy( jd(sglist[tail] , sglist[tail-1]) , sglist[head])==false )tail--;
    while(head<tail && satisfy( jd(sglist[head] , sglist[head+1]) , sglist[tail])==false )head++;

ok，到这里我们的问题已经解决了一大半了。现在我们先要判断无解情况，什么时候无解？我们都知道，三条直线才能围成封闭的图形，所以如果此时队列元素少于等于两个，就是无解。

接着对于有解情况，我们只需要记录任意两条相邻边的交点，然后利用叉积中讲到的第二种方法，利用叉积面积上的几何意义（multi的绝对值是三点组成三角形面积的两倍）求解该多变形面积。

所以这整一块的代码如下：

bool cmp(segment sg1,segment sg2)
{
    if( sg1.angle<sg2.angle )return(true);
    if( fabs(sg1.angle-sg2.angle)<eps && satisfy(sg1.p1,sg2)==true)return(true);
    return(false);
}

void HPI()
{
    sort(seg+1,seg+n+1,cmp);
    int tp=1;
    for(int i=2;i<=n;i++)if(seg[i].angle-seg[tp].angle> eps )seg[++tp]=seg[i];
    n=tp;
    sglist[1]=seg[1];sglist[2]=seg[2];
    head=1;tail=2;
    for(int i=3;i<=n;i++)
    {
        while(head<tail && satisfy( jd(sglist[tail] , sglist[tail-1]) , seg[i])==false )tail--;
        while(head<tail && satisfy( jd(sglist[head] , sglist[head+1]) , seg[i])==false )head++;
        sglist[++tail]=seg[i];
    }

    while(head<tail && satisfy( jd(sglist[tail] , sglist[tail-1]) , sglist[head])==false )tail--;
    while(head<tail && satisfy( jd(sglist[head] , sglist[head+1]) , sglist[tail])==false )head++;

    if(tail-head+1<=2)
    {
        printf("0.0");
        return;
    }

    pl=0;
    for(int i=head;i<tail;i++)plist[++pl]=jd(sglist[i],sglist[i+1]);
    plist[++pl]=jd(sglist[head],sglist[tail]);

    double ans=0.0;
    for(int i=3;i<=pl;i++)ans=ans+multi(plist[i],plist[i-1],plist[1]);
    ans=fabs(ans)/2.0;

    printf("%0.1lf",ans);
}

模板模板题

【caioj 1215】求半平面交的面积

题目描述
【题意】
在一个有限大（-10 0000<=x,y<=10 0000)的平面坐标系上有n个半平面（注意有限的），每个半平面给出一条有向线段（x1,y1)——>(x2,y2）。
每个半平面的有效区域都是左侧。求这n个半平面的交的面积。
【输入文件】
第一行一个整数n（1 <= n <= 2 0000）
下来n个半平面。每个半平面一行四个整数x1,y1,x2,y2。（-100000 <= x1,y1,x2,y2 <= 100000)
【输出文件】
一行，输出n个半平面的交的面积（保留一位小数），如果有效面积不存在则输出"0.0"。
【样例1输入】
3
1 1 9 9
5 10 4 10
0 3 0 2
【样例1输出】
50.0
【样例2输入】
4
0 0 10 0
10 0 10 10
10 10 0 10
11 11 11 0
【样例2输出】
0.0

这道题很明显是一道模板题，只需要按上面说的打一遍半平面交面积就好啦，值得注意的是，由于有边界的存在，所以要加入四条表示边界（-100000.0到100000）的有向直线

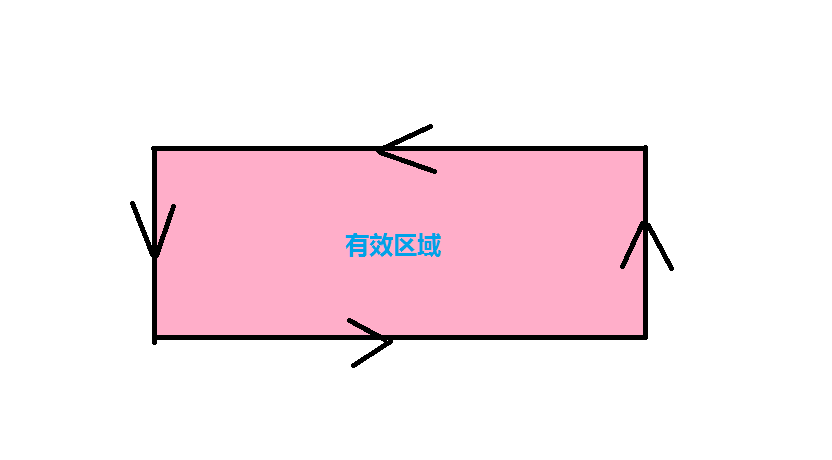
这里贴一下模板（代码）：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#define eps 1e-8
using namespace std;
const int Maxn=21000;
double Maxx=100000.0;
double Minn=-100000.0;

struct point
{
    double x,y;
}plist[Maxn];int pl;

struct segment
{
    point p1,p2;
    double angle;//该直线斜率
    segment(){}
    segment(double x1,double y1,double x2,double y2)
    {
        p1.x=x1;p1.y=y1;
        p2.x=x2;p2.y=y2;
    } 

    void get_angle()
    {
        angle=atan2(p2.y-p1.y,p2.x-p1.x);
    }
}seg[Maxn],sglist[Maxn];int head,tail;
int n;

double multi(point p1,point p2,point p0)
{
    double x1=p1.x-p0.x;
    double y1=p1.y-p0.y;
    double x2=p2.x-p0.x;
    double y2=p2.y-p0.y;
    return(x1*y2-x2*y1);
}

point jd(segment sg1,segment sg2)
{
    point p,p1=sg1.p1,p2=sg1.p2,p3=sg2.p1,p4=sg2.p2;
    double t1=multi(p1,p4,p3);
    double t2=multi(p2,p4,p3);

    p.x=(t1*p2.x-t2*p1.x)/(t1-t2);
    p.y=(t1*p2.y-t2*p1.y)/(t1-t2);

    return(p);
}

bool satisfy(point p,segment sg)
{
    if(multi(p,sg.p2,sg.p1)<=eps)return true;
    else return false;
}

bool cmp(segment sg1,segment sg2)
{
    if( sg1.angle<sg2.angle )return(true);
    if( fabs(sg1.angle-sg2.angle)<eps && satisfy(sg1.p1,sg2)==true)return(true);
    return(false);
}

void HPI()
{
    sort(seg+1,seg+n+1,cmp);
    int tp=1;
    for(int i=2;i<=n;i++)if(seg[i].angle-seg[tp].angle> eps )seg[++tp]=seg[i];
    n=tp;
    sglist[1]=seg[1];sglist[2]=seg[2];
    head=1;tail=2;
    for(int i=3;i<=n;i++)
    {
        while(head<tail && satisfy( jd(sglist[tail] , sglist[tail-1]) , seg[i])==false )tail--;
        while(head<tail && satisfy( jd(sglist[head] , sglist[head+1]) , seg[i])==false )head++;
        sglist[++tail]=seg[i];
    }

    while(head<tail && satisfy( jd(sglist[tail] , sglist[tail-1]) , sglist[head])==false )tail--;
    while(head<tail && satisfy( jd(sglist[head] , sglist[head+1]) , sglist[tail])==false )head++;

    if(tail-head+1<=2)
    {
        printf("0.0");
        return;
    }

    pl=0;
    for(int i=head;i<tail;i++)plist[++pl]=jd(sglist[i],sglist[i+1]);
    plist[++pl]=jd(sglist[head],sglist[tail]);

    double ans=0.0;
    for(int i=3;i<=pl;i++)ans=ans+multi(plist[i],plist[i-1],plist[1]);
    ans=fabs(ans)/2.0;

    printf("%0.1lf",ans);
}

int main()
{
    scanf("%d",&n);
    seg[1]=segment(Minn,Minn,Maxx,Minn);seg[1].get_angle();
    seg[2]=segment(Maxx,Minn,Maxx,Maxx);seg[2].get_angle();
    seg[3]=segment(Maxx,Maxx,Minn,Maxx);seg[3].get_angle();
    seg[4]=segment(Minn,Maxx,Minn,Minn);seg[4].get_angle();

    double x1,x2,y1,y2;
    for(int i=1;i<=n;i++)
    {
        scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
        seg[i+4]=segment(x1,y1,x2,y2);
        seg[i+4].get_angle();
    }

    n+=4;
    HPI();
    return 0;

} 
/*
point jd(segment sg1,segment sg2)
{
    point p1,p2,p3,p4,ret;
    p1=sg1.p1;p2=sg1.p2;
    p3=sg2.p1;p4-sg2.p2;

    double a1,a2,b1,b2,c1,c2;

    a1=p1.y-p2.y;
    b1=p2.x-p1.x;
    c1=p1.x*p2.y-p2.x*p1.y;
    //计算出第一条直线的方程 

    a2=p3.y-p4.y;
    b2=p4.x-p3.x;
    c2=p3.x*p4.y-p4.x*p3.y;
    //计算出第二条直线的方程 

    ret.x=(c1*b2-c2*b1)/(a2*b1-a1*b2);
    ret.y=(c2*a1-c1*a2)/(a2*b1-a1*b2);
    //计算出交点 
    return ret;
}
*/

结语

通过这篇BLOG，相信你已经对半平面交有一点感觉了，还是那句话，希望大家能在计算几何的路上越走越远,感谢你的阅读！
一些值得做的题目：

pku3130 按照逆时针给出点的坐标，求是否存在这些点围成的多边形的核 半平面交 所谓多边形的核就是过这个点的所有直线可以覆盖整个多边形。半平面交的裸模板
pku3335 按照顺时针给出点的坐标，求是否存在这些点围成的多边形的核 半平面交 同上，但要注意顺时针与逆时针的不同
pku1474 同上 半平面交 同上
pku1279 按照顺时针给出点的坐标，求这个多边形的核的面积 半平面交 求面积即可
pku3525 按照逆时针给出点，求该多边形内某一点使得该点到所有边的距离的最小值最大 半平面交 二分答案，把多边形往内缩
pku3384 按照顺时针给出点，求在这个多边形里画两个半径为r的圆，使得覆盖面积最大，问两个圆的圆心坐标 半平面交 把每条边都往里缩r，然后找最远的两个点即可
pku1755 有n个人要参加铁人三项，他们每一项的速度为ui、vi、wi，问可否通过修改每一段的路程使得这个人得冠军 半平面交 用半平面交解方程组。注意判断a=0、b=0的情况
pku2540 在一个(0,0)(0,10)(10,0)(10,10)的范围内，有一个点是要你去找的，从(0,0)开始每次给出一个点的坐标，再给出要找的点对于前一个点和现在给出的点是接近了还是更远了，求要找的点可行范围的面积 半平面交 半平面交求可行域，每一次就以给出的点和前一个点作中垂线即可
pku2451 在[0,10000][0,10000]里面给出n条直线，求半平面交 半平面交 n<=20000要用nlogn的半平面交计算
hdu3761 有n个瞭望台形成一个凸多边形，敌人会炸你的瞭望台，请选择一个点作为总部，使得敌人需要炸的瞭望台尽量多 半平面交 自己想，敌人最优的炸方案肯定是连着炸。二分答案求是否可行