在最近的训练中,遇到了很多与LCA有关的算法。今天就让我们一起来重温一下求解LCA的三种主流算法吧!
LCA简介
在求解LCA之前,我们需要先知道什么叫LCA。LCA(Least Common Ancestors),即最近公共祖先,是指在有根树或者DAG中,某两个结点u和v最近的公共祖先。
觉得很迷?没问题,下面我们来通过一个例子来理解一下LCA的内涵,我们首先有一颗可爱的树(特别感谢大佬的图):
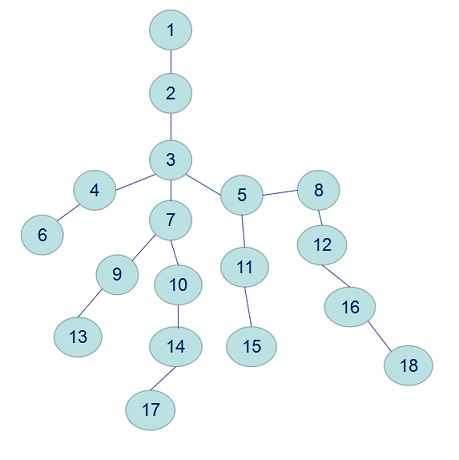
在这棵树中,6和13的LCA就是3(见蓝线),11和18的LCA就是5(见橙线):
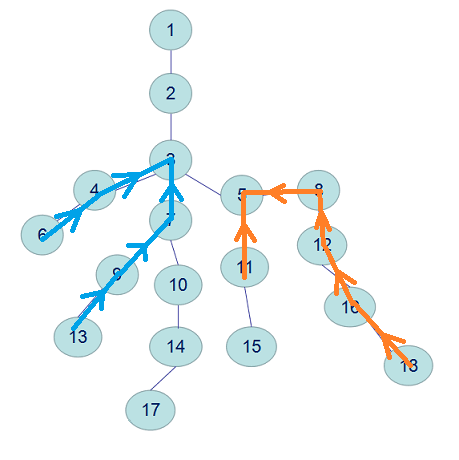
知道了LCA的概念以后,我们应该要如何求解LCA呢?暴力?暴力求解单次求解就到了O(n),m次查询的话时间复杂度就到了O(mn),m,n较大时,一条链的结构就能轻松卡掉。那么有没有什么比较快的算法呢?
倍增(在线)
算法介绍
在求解LCA的算法中,倍增应该是用的最多的在线算法,其复杂度也才O(nlogn+mlogn)[n为点数,m为询问数]。何谓在线呢?感性理解就是对于每个读入我都单独查询一遍,就类似在线聊天,它给我一个问题,我处理后返回答案给它。而所谓倍增,就是按2的倍数来增大,也就是跳1,2,4,8,16,32…… 不过在这我们不是按从小到大跳,而是从大向小跳,即按……32,16,8,4,2,1来跳,如果大的跳不过去,再把它调小,判断是否能跳,这是为什么呢?这是因为从小开始跳,可能会出现超出或者填不满的现象。
拿 5 为例,从小向大跳,1+2<5<1+2+4,若按从小到大的顺序能跳就跳就永远跳不到5了,所以这时我们还要回溯一步,不跳2,然后才能得出5=1+4,这样就增加了程序的运行时间;而从大向小跳,直接可以得出5=4+1。这也可以拿二进制为例,5(101),从高位向低位填很简单,如果填了这位之后比原数大了,那我就不填。其实就相当于在二进制下从高位到低位取二进制下为1的位数,就如5(101),在二进制下第二位和第零位都是1,所以5=4+1=2^2+2^0,这个过程是很好操作的。
还是以 6 和 13 为例,在倍增找LCA的过程中,我们访问的节点只有:
6−>3
13−>7−>3
从中可以看出此时向上跳的次数大大减小。这个算法的时间复杂度为O(mlogn),已经可以满足大部分在线求解LCA的需求。
算法实现
想要实现这个算法,首先我们要记录各个点的深度和他们2^i级的的祖先,用数组depth[i]表示每个节点的深度,fa[i][j]表示节点i的2^j级祖先,特别地,当j=0时,fa[i][j]即为i的父亲,我们在开始时先预处理出fa数组,代码如下:
void dfs(int f,int fath)//预处理fa数组
//f表示当前节点,fath表示它的父亲节点
{
depth[f]=depth[fath]+1;//记录f点深度
fa[f][0]=fath;//f的2^0=1级祖先是他的父亲
for(int i=1;(1<<i)<=depth[f];i++)//如果有2^i级祖先
fa[f][i]=fa[fa[f][i-1]][i-1];
//f的2^i级祖先等于f的2^(i-1)级祖先的2^(i-1)级祖先,即2^i=2^(i-1)+2^(i-1)
for(int i=last[f];i;i=a[i].next)
if(a[i].y!=fath)dfs(a[i].y,f);
//继续dfs其儿子节点
}预处理完毕后,我们就可以去找它的LCA了,为了让它跑得快一些,我们可以再把log2(i)预处理出来:
for(int i=1;i<=n;i++)lg[i]=lg[i/2]+1;
//预先算出log2(i)+1的值,方便后续计算 接下来就是通过倍增求解LCA了,首先我们要把两个节点跳到同一深度在开始跳。而且我们在跳的时候不能直接跳到它们的LCA,因为这可能会误判。如下图,比如4和8,在跳的时候,我们可能会认为1是它们的LCA,但1只是它们的祖先,它们的LCA其实是3。所以我们要跳到它们LCA的下面一层,比如4和8,我们就跳到4和5,然后输出它们的父节点,这样就不会误判了。

代码如下:
int lca(int x,int y)//LCA
{
if(depth[x]<depth[y])swap(x,y);//默认的深度比y深
while(depth[x]>depth[y])x=fa[x][lg[depth[x]-depth[y]]-1];
//让x和y跳到同一深度
if(x==y)return y;
//如果到同一深度后x==y代表y是x的祖先,返回y即可
for(int k=lg[depth[x]]-1;k>=0;k--)
if(fa[x][k]!=fa[y][k])
{
x=fa[x][k];
y=fa[y][k];
}//从大向小跳
return fa[x][0];
}所以之前那个例子,求6和13的完整路径应该是:
13−>9->7−>3
6−>4->3
经典例题
[luoguP3379] 【模板】最近公共祖先(LCA)
题目描述
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。输入格式
第一行包含三个正整数N、M、S,分别表示树的结点个数、询问的个数和树根结点的序号。接下来N-1行每行包含两个正整数x、y,表示x结点和y结点之间有一条直接连接的边(数据保证可以构成树)。
接下来M行每行包含两个正整数a、b,表示询问a结点和b结点的最近公共祖先。
输出格式
输出包含M行,每行包含一个正整数,依次为每一个询问的结果。输入输出样例
输入 #1
5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5
输出 #1
4
4
1
4
4
说明/提示
时空限制:1000ms,128M数据规模:
对于30%的数据:N<=10,M<=10
对于70%的数据:N<=10000,M<=10000
对于100%的数据:N<=500000,M<=500000
这就是LCA的板子了,直接贴上模板:
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
int x,y,next;
}a[2*500001];
int depth[500001],fa[500001][22],lg[500001],last[500001];
//depth[i]表示i号点在树上的深度
//fa[i][j]表示i的2^j级祖先是谁
//lg[i]表示log2(i)+1是多少
int tot;
void add(int x,int y) //邻接表存树
{
tot++;
a[tot].x=x;a[tot].y=y;
a[tot].next=last[x];
last[x]=tot;
}
void dfs(int f,int fath)//预处理fa数组
//f表示当前节点,fath表示它的父亲节点
{
depth[f]=depth[fath]+1;//记录f点深度
fa[f][0]=fath;//f的2^0=1级祖先是他的父亲
for(int i=1;(1<<i)<=depth[f];i++)//如果有2^i级祖先
fa[f][i]=fa[fa[f][i-1]][i-1];
//f的2^i级祖先等于f的2^(i-1)级祖先的2^(i-1)级祖先,即2^i=2^(i-1)+2^(i-1)
for(int i=last[f];i;i=a[i].next)
if(a[i].y!=fath)dfs(a[i].y,f);
//继续dfs其儿子节点
}
int lca(int x,int y)//LCA
{
if(depth[x]<depth[y])swap(x,y);//默认的深度比y深
while(depth[x]>depth[y])x=fa[x][lg[depth[x]-depth[y]]-1];
//让x和y跳到同一深度
if(x==y)return y;
//如果到同一深度后x==y代表y是x的祖先,返回y即可
for(int k=lg[depth[x]]-1;k>=0;k--)
if(fa[x][k]!=fa[y][k])
{
x=fa[x][k];
y=fa[y][k];
}//从大向小跳
return fa[x][0];
}
int n,m,s;
int main()
{
scanf("%d%d%d",&n,&m,&s);
for(int i=1;i<=n-1;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);//连边
}
dfs(s,0);//预处理
for(int i=1;i<=n;i++)lg[i]=lg[i/2]+1;
//预先算出log2(i)+1的值,方便后续计算
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
printf("%d\n",lca(x,y));
}
return 0;
}欧拉序+ST表(在线)
算法介绍
当然不仅有倍增这一算法能在线求解LCA,欧拉序+ST表也可以实现O(nlogn)预处理,O(1)查询地在线求解LCA。相较于倍增,除了时间更优,你可能会问了,它还特别在什么地方呢?啊哈,它还特别就特别在它支持换根操作!至于如何实现,别急,先从欧拉序是什么开始吧。
什么是欧拉序呢?顾名思义,就是一个叫欧拉的人定义的一种树上DFS序,那么欧拉和我们传统的DFS序有什么区别呢?我们来通过例子一探究竟:
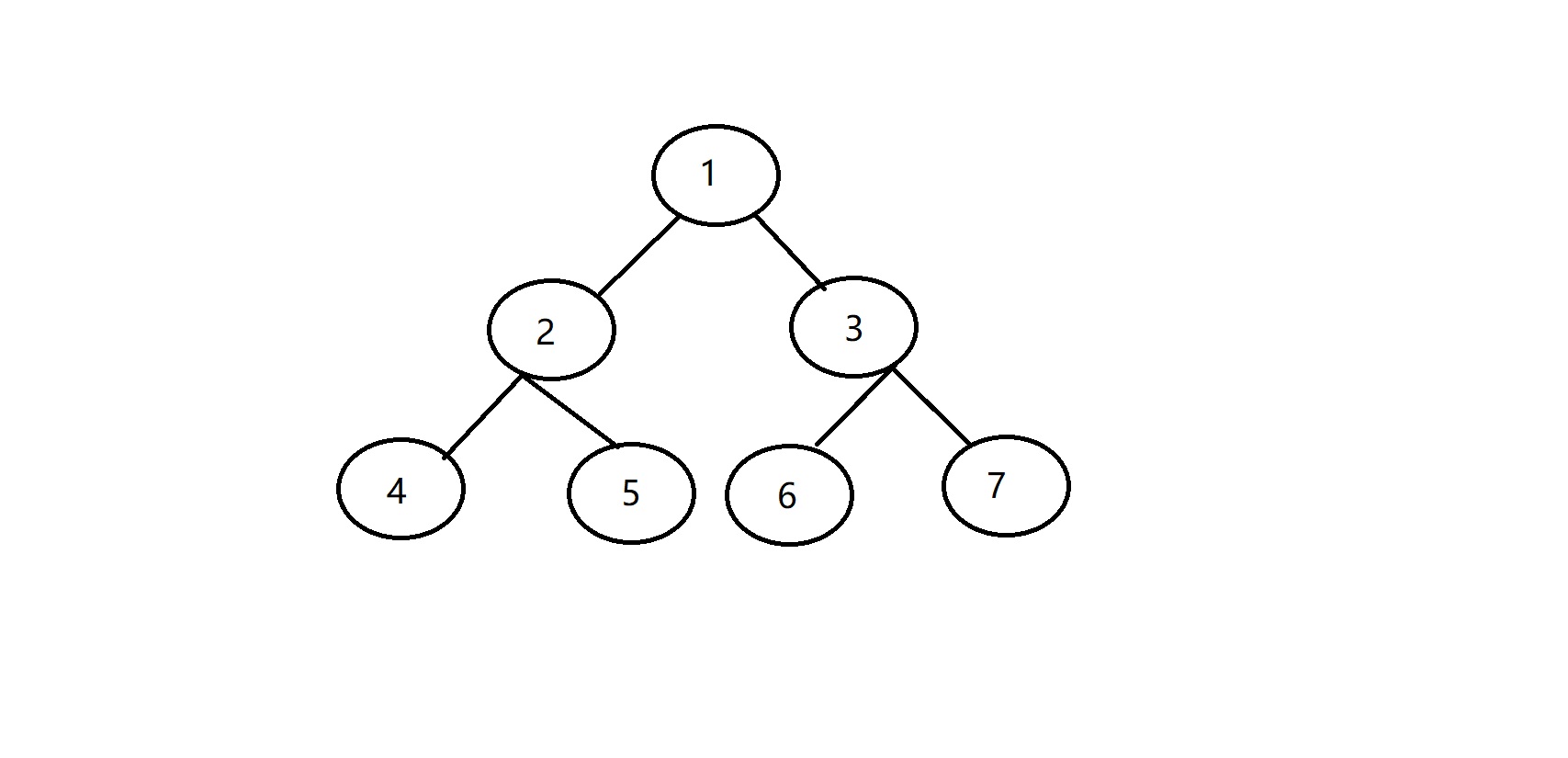
我们一般的DFS序,是在第一次访问到某个节点时,记录一次访问的时间戳(也就是在DFS序上的位置),比如,如果按照下图的访问顺序,按时间排序的DFS序就应该为 1 2 4 5 3 6 7:
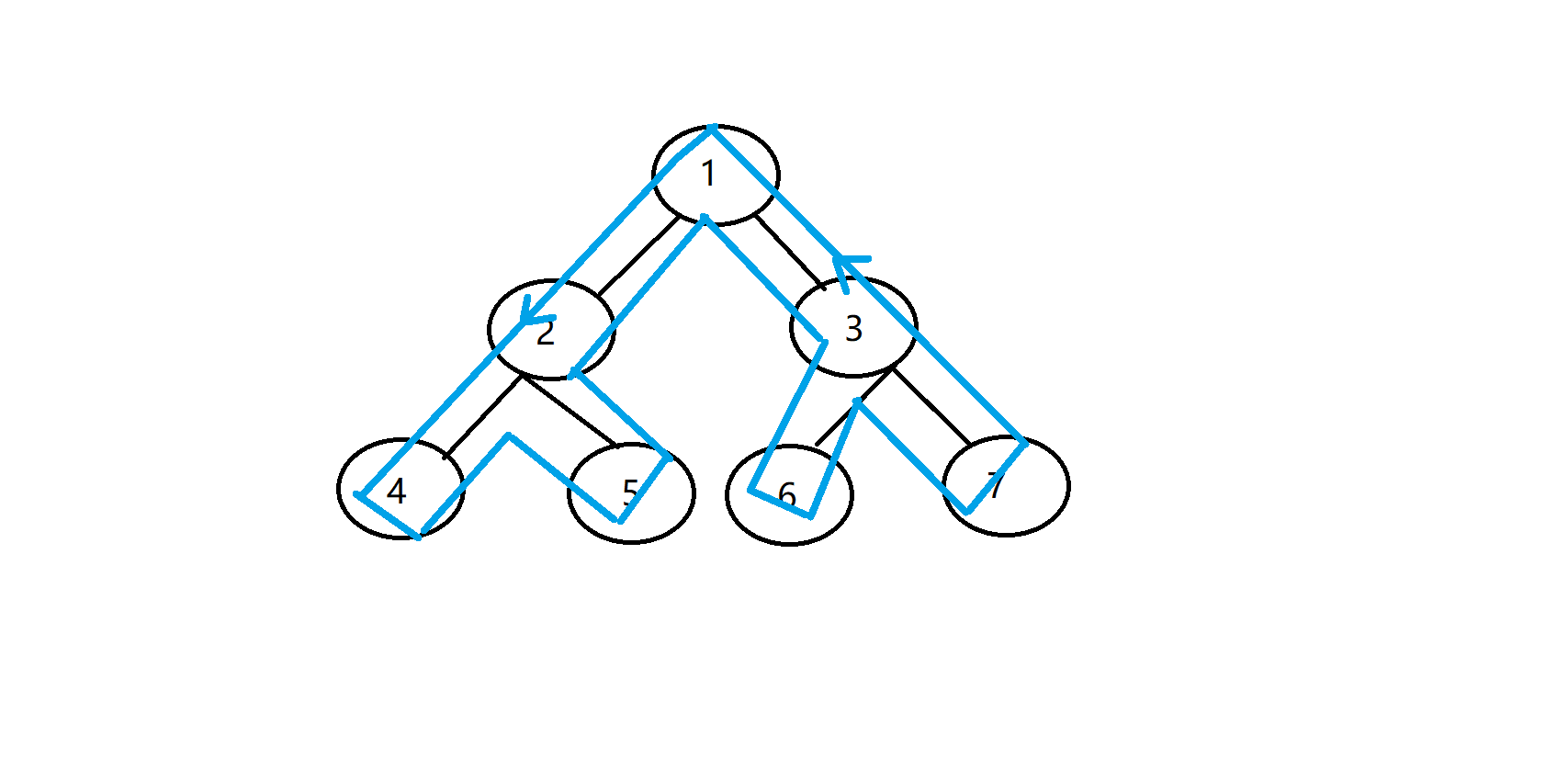
不同于普通的DFS序,欧拉序是在每一次访问到某个节点时都记录一次访问的时间戳(也就是在欧拉序上的位置),比如,仍是按上图的访问顺序,按时间戳排序的欧拉序就应该为 1 2 4 2 5 2 1 3 6 3 7 3 1;
求出欧拉序后,我们又要如何操作呢?
假设现我们需要求x和y的LCA,我们设st[i]为第一次访问到i号节点的时间戳(也就是在欧拉序上的位置),ed[i]为离开到i号节点的时间戳(也就是在欧拉序上的位置);我们假定st[x]<st[y],跑一遍欧拉序并记录st[i]和ed[i]后,st[x],st[y],ed[x],ed[y]的大小关系只有两种情况(交换后):
1.st[x]<st[y]<=ed[y]<=ed[x],表示x是y的祖先。
此时x与y的LCA就是x。
2.st[x]<=ed[x]<st[y]<=ed[y],表示x与y没有祖先-后裔关系。
此时我们观察欧拉序,在st[x]与st[y]之间的节点中深度最小的节点,就是x与y的LCA。
而在实现时,我们先对先对欧拉序建立st表,比较规则是选择深度小的,查询只要查询ed[x]与st[y]之间深度最小的节点即可。
但实际上,我们可以不用额外统计深度,而把比较规则改为选择ed[x]与st[y]中st最小的。这是为什么呢?因为在欧拉序上,最近公共祖先一定只访问一次,且是两者的祖先,而祖先的st一定小于其直系后代的st,所以在ed[x]与st[y]之间深度最小的节点即最高处的祖先st一定最小,故只要查询ed[x]与st[y]中st最小的节点就可以啦。
那如何快速查找ed[x]与st[y]中st最小的节点呢?使用st表就能在O(1)的时间复杂度下完成查询。还不会st表的同学可以点击这里。
然而,在程序实现中,由于x有可能是y的祖先,导致ed[x]>st[y],要进行特判;所以在程序实现中,往往直接查找st[x]与st[y]中st最小的节点,这和查找ed[x]与st[y]中st最小的节点其实是等效的。这是为什么呢?这是因为st[x]和ed[x]中的节点都是x的子代,其st值一定大于st的祖先也就是我们的最后答案,所以对答案没有影响,故是等效的。
算法实现
弄清思路以后,实现其实就很简单了。算法主要分为三个部分,首先是预处理出euler序和st及ed数组:
void dfs(int f,int fath)//预处理欧拉序和st,ed数组
//f表示当前节点,fath表示它的父亲节点
{
tim++;
euler[tim]=f;st[f]=tim;value[tim]=f;//记录第一次访问到f节点的时间戳
for(int i=last[f];i;i=a[i].next)
if(a[i].y!=fath)
{
dfs(a[i].y,f);
tim++;euler[tim]=f;//每次访问到该节点都记录一次
}
//继续dfs其儿子节点
ed[f]=tim;//记录离开f节点的时间戳
}接着是预处理出st表:
void my_st()//st表预处理
{
for(int i=1;i<=tim;i++)s[i][0]=st[euler[i]];
bin[0]=1;for(int i=1;i<=30;i++)bin[i]=bin[i-1]*2;
logg[0]=-1;for(int i=1;i<=tim;i++)logg[i]=logg[i/2]+1;
for(int i=1;i<=logg[tim];i++)
for(int j=1;j<=tim;j++)
{
if(j+bin[i]-1<=tim)
{
s[j][i]=min(s[j][i-1],s[j+bin[i-1]][i-1]);
}
}
} 最后是在st表上查询答案:
int qurry(int x,int y)//st表查询
{
if(st[x]>st[y])swap(x,y);
int xx=st[x],yy=st[y];
int t=yy-xx+1,lg=logg[t];
return(value[min(s[xx][lg],s[yy-bin[lg]+1][lg])]);
//查询st值最小的那个对应的节点序号
} 经典例题
[luoguP3379] 【模板】最近公共祖先(LCA)
题目描述
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。输入格式
第一行包含三个正整数N、M、S,分别表示树的结点个数、询问的个数和树根结点的序号。接下来N-1行每行包含两个正整数x、y,表示x结点和y结点之间有一条直接连接的边(数据保证可以构成树)。
接下来M行每行包含两个正整数a、b,表示询问a结点和b结点的最近公共祖先。
输出格式
输出包含M行,每行包含一个正整数,依次为每一个询问的结果。输入输出样例
输入 #1
5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5
输出 #1
4
4
1
4
4
说明/提示
时空限制:1000ms,128M数据规模:
对于30%的数据:N<=10,M<=10
对于70%的数据:N<=10000,M<=10000
对于100%的数据:N<=500000,M<=500000
还是刚刚那道题,直接贴上模板:
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
int x,y,next;
}a[2*500001];
int st[500001],ed[500001],euler[4*500001],value[4*500001],last[500001];
//st[i]为第一次访问到i号节点的时间戳(也就是在欧拉序上的位置)
//ed[i]为离开到i号节点的时间戳(也就是在欧拉序上的位置)
//euler数组存储按时间戳排序的欧拉序
//关于euler序的大小,如果叶子只统计一次就为2*n,但是如果统计两次就是4*n,怎么证明呢?对于每个点,其访问次数等于1+其儿子节点个数,所以euler序的大小就是 n+(n-1)=2n-1,但我习惯开大成4*n了QwQ
//value[i]表示st值为i的节点是谁(用于st表查询)
int s[4*500001][30],logg[4*500001],bin[33];
//st表用到的数组
int tot,tim;
void add(int x,int y) //邻接表存树
{
tot++;
a[tot].x=x;a[tot].y=y;
a[tot].next=last[x];
last[x]=tot;
}
void dfs(int f,int fath)//预处理欧拉序和st,ed数组
//f表示当前节点,fath表示它的父亲节点
{
tim++;
euler[tim]=f;st[f]=tim;value[tim]=f;//记录第一次访问到f节点的时间戳
for(int i=last[f];i;i=a[i].next)
if(a[i].y!=fath)
{
dfs(a[i].y,f);
tim++;euler[tim]=f;//每次访问到该节点都记录一次
}
//继续dfs其儿子节点
ed[f]=tim;//记录离开f节点的时间戳
}
void my_st()//st表预处理
{
for(int i=1;i<=tim;i++)s[i][0]=st[euler[i]];
bin[0]=1;for(int i=1;i<=30;i++)bin[i]=bin[i-1]*2;
logg[0]=-1;for(int i=1;i<=tim;i++)logg[i]=logg[i/2]+1;
for(int i=1;i<=logg[tim];i++)
for(int j=1;j<=tim;j++)
{
if(j+bin[i]-1<=tim)
{
s[j][i]=min(s[j][i-1],s[j+bin[i-1]][i-1]);
}
}
}
int qurry(int x,int y)//st表查询
{
if(st[x]>st[y])swap(x,y);
int xx=st[x],yy=st[y];
int t=yy-xx+1,lg=logg[t];
return(value[min(s[xx][lg],s[yy-bin[lg]+1][lg])]);
//查询st值最小的那个对应的节点序号
}
int n,m,ro;
int main()
{
scanf("%d%d%d",&n,&m,&ro);
for(int i=1;i<=n-1;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);//连边
}
dfs(ro,0);//预处理
my_st();//st表预处理
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
printf("%d\n",qurry(x,y));//输出答案
}
return 0;
}换根操作
最后我们再来介绍一下欧拉序的骚操作——换根。在换根后,倍增就要重新dfs构造倍增数组,这就会导致TLE。但是欧拉序不用,这是为什么呢?
我们先举个例子:
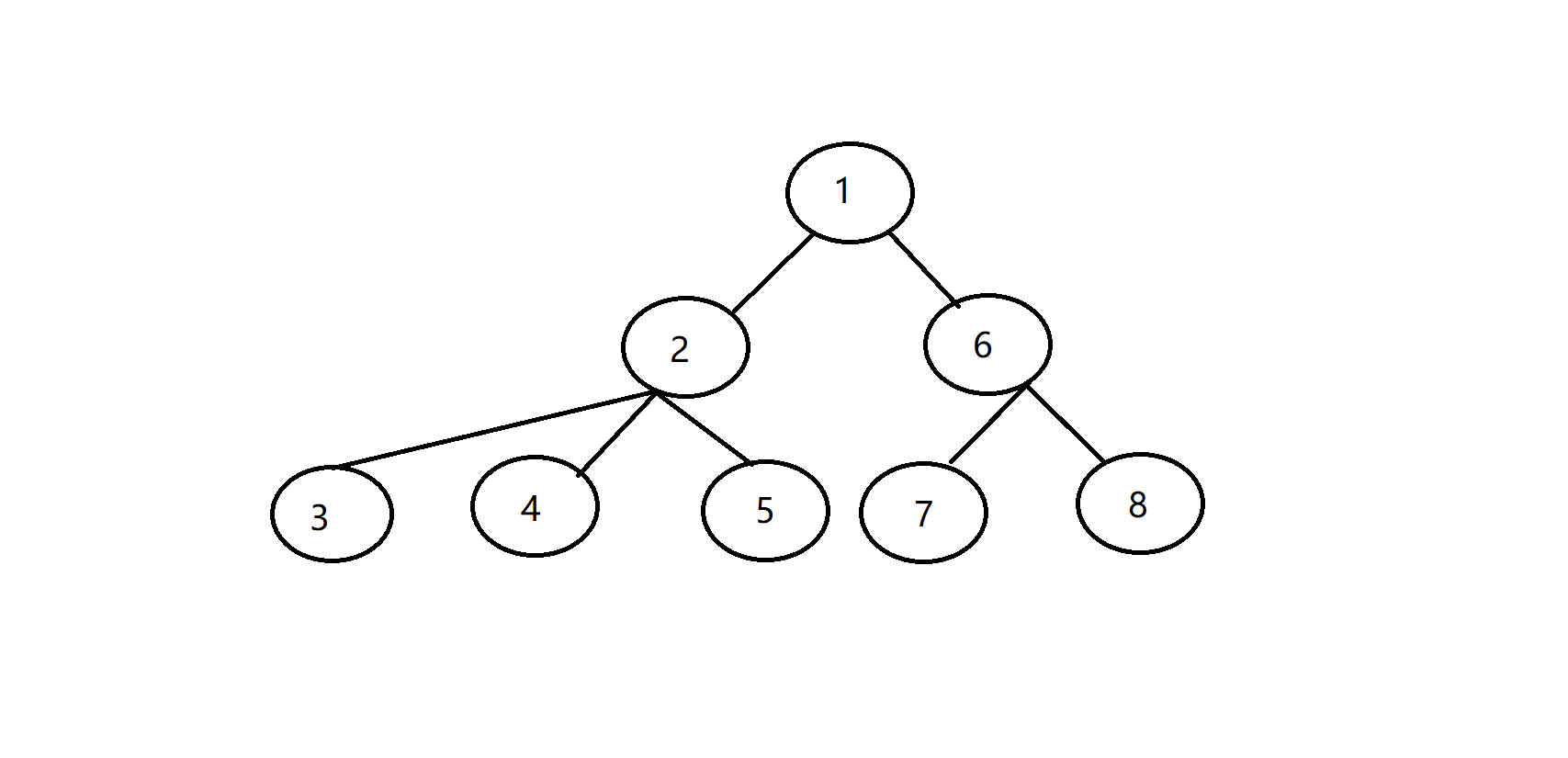
以上面这棵可爱的树为例子,欧拉序其实相当于以根为起点围着树跑了一圈,那么我们就可以把欧拉序写成一个环就是:
1 2 3 2 4 2 5 2 1 6 7 6 8 6 1 2 3 2 4 2 5 2 1 6 7 6 8 6
以某个点为跟的欧拉序就是以某个点在上面的欧拉序中第一次出现的位置为起点向前走(2*n-1)步,例如以4为根的欧拉序就是:
1 2 3 2 4 2 5 2 1 6 7 6 8 6 1 2 3 2 4 2 5 2 1 6 7 6 8 6
这样就能很轻易的完成换根操作啦!
Tarjan(离线)
算法介绍
Tarjan是我们介绍的三种算法中唯一的离线算法。那么相对于在线,什么是离线呢?离线算法,是指首先读入所有的询问(求一次LCA叫做一次询问),然后重新组织查询处理顺序以便得到更高效的处理方法。简而言之,就是把所有要求x,y的LCA的读入数据先读入,再在算法中一起完成查询,其时间复杂度达到了O(n+m)。
那么神奇的Tarjan算法的原理是什么呢?在了解具体流程之前我们先来听一个故事吧:
一个熊孩子Link从一棵有根树的最左边最底下的结点灌岩浆,Link表示很讨厌这种倒着长的树。岩浆会不断的注入,直到注满整个树…如果岩浆灌满了一棵子树,且发现树的旁边有一另一棵子树,Link会先去将那棵子树灌满。岩浆只有在迫不得已的情况下才会向上升高,找到一个新的子树继续注入。机智的Link发现了找LCA的好方法,即如果两个结点都被岩浆烧掉时,他们的LCA即为那棵子树上岩浆最高的位置。
—— riteme
没错,这正是Tarjan算法的主要思路。没听懂?没关系,我们具象化一下Tarjan算法的思路(PS Tarjan大佬真的很喜欢并查集QwQ):
1.任选一个点为根节点,从根节点开始进行DFS;
2.设当前DFS到点u,遍历该点u所有子节点v;
3.若是v还有子节点,返回2,否则下一步;4.在并查集中,将合并v到u上,并标记节点v已被访问过;
5.寻找与当前点u有询问关系的点x;
6.若是x已经被访问过了,则可以确认u和x的最近公共祖先为x所在的并查集的根节点。
伪代码为:
Tarjan(u)//marge和find为并查集合并函数和查找函数
{
for each(u,v) //访问所有u子节点v
{
Tarjan(v); //继续往下遍历
marge(u,v); //合并v到u上
标记v被访问过;
}
for each(u,e) //访问所有和u有询问关系的e
{
如果e被访问过;
u,e的最近公共祖先为find(e);
}
}什么还是不太理解?没事,下面我们就通过一个例子来帮助大家深入理解。
我们首先有一棵树,我们要查询四组点的LCA,分别是(1,3),(3,4),(2,5),(4,6),我们先将并查集中每个节点的父亲设置为自己。我们设节点i为白色则代表vis[i]=0,即代表没访问过,反之,若为蓝色则代表vis[i]=1,即代表访问过,开始状态如下:
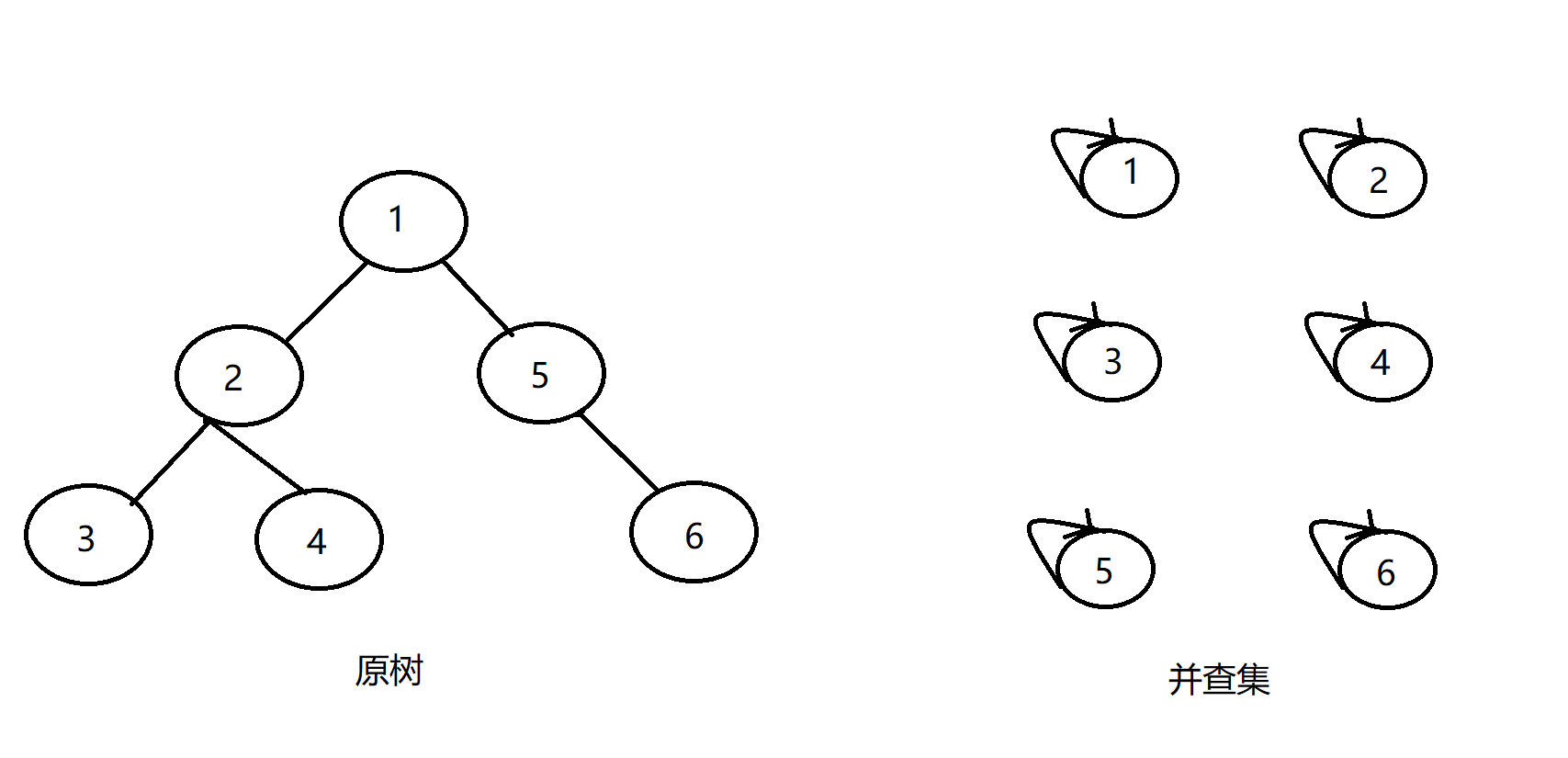
首先我们以以1为根节点,往下搜索发现有两个儿子2和5;
先搜2,发现2有两个儿子3和4,先搜索3,发现3没有子节点,则寻找在查询中与其有关系的点;
发现1与3有关系,但是vis[1]=0,即1还没被搜过,所以不操作;又发现4与3有关系,但是vis[4]=0,即4还没被搜过,所以也不操作;
发现没有和3有询问关系的点了,返回此前一层的搜索,将3的父亲节点设为2,更新vis[3]=1:
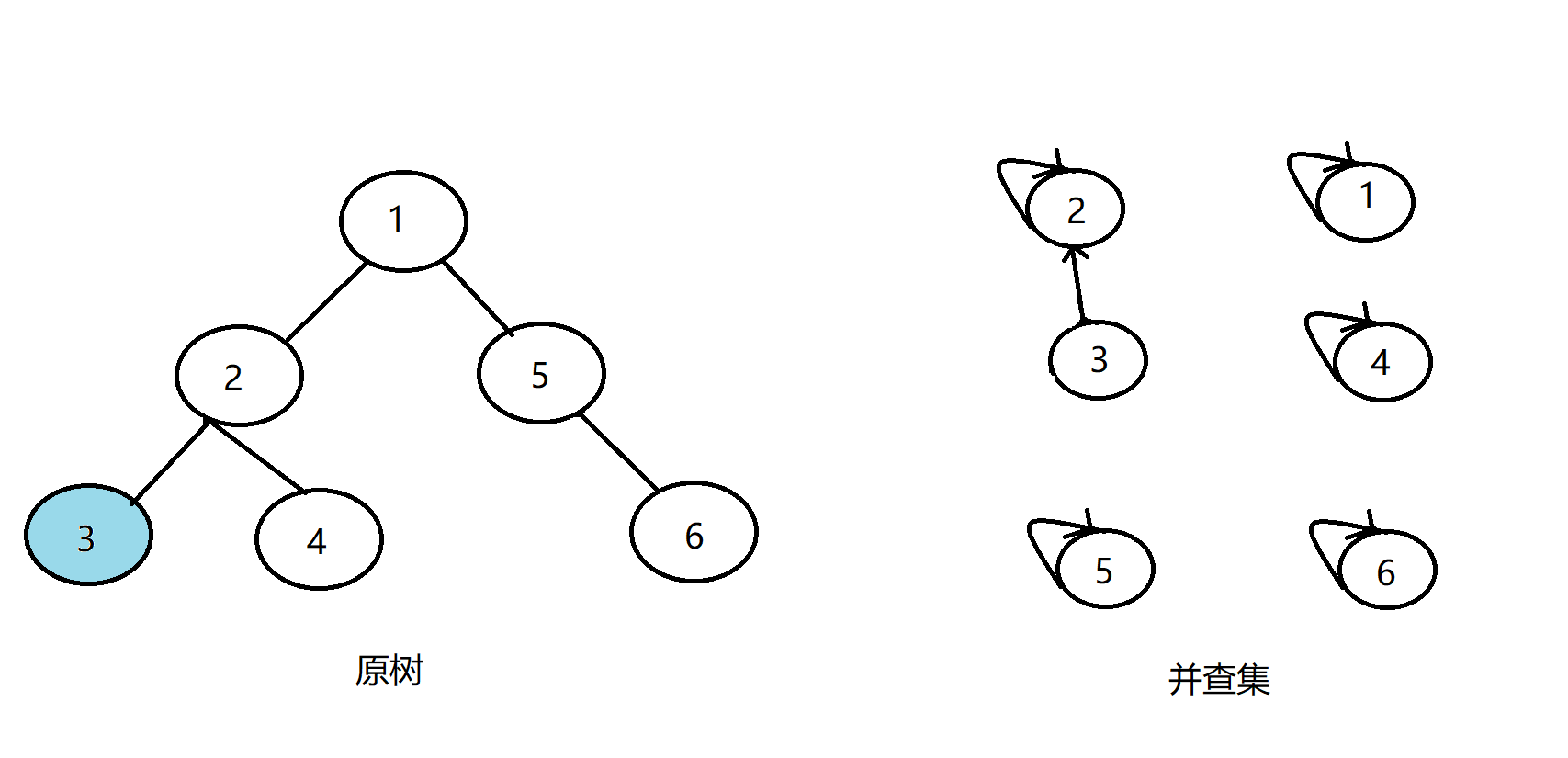
继续搜索4,发现4没有子节点,则寻找在查询中与其有关系的点;
发现6与4有关系,但vis[6]=0,即1还没被搜过,所以不操作;但这时我们发现,发现3与4有关系,且vis[3]=1,即3已经被搜过,所以这时记录答案——4和3的LCA即为3所在并查集的根节点——find(3)=2!
发现没有和4有询问关系的点了,返回此前一层的搜索,将4的父亲节点设为2,更新vis[4]=1:
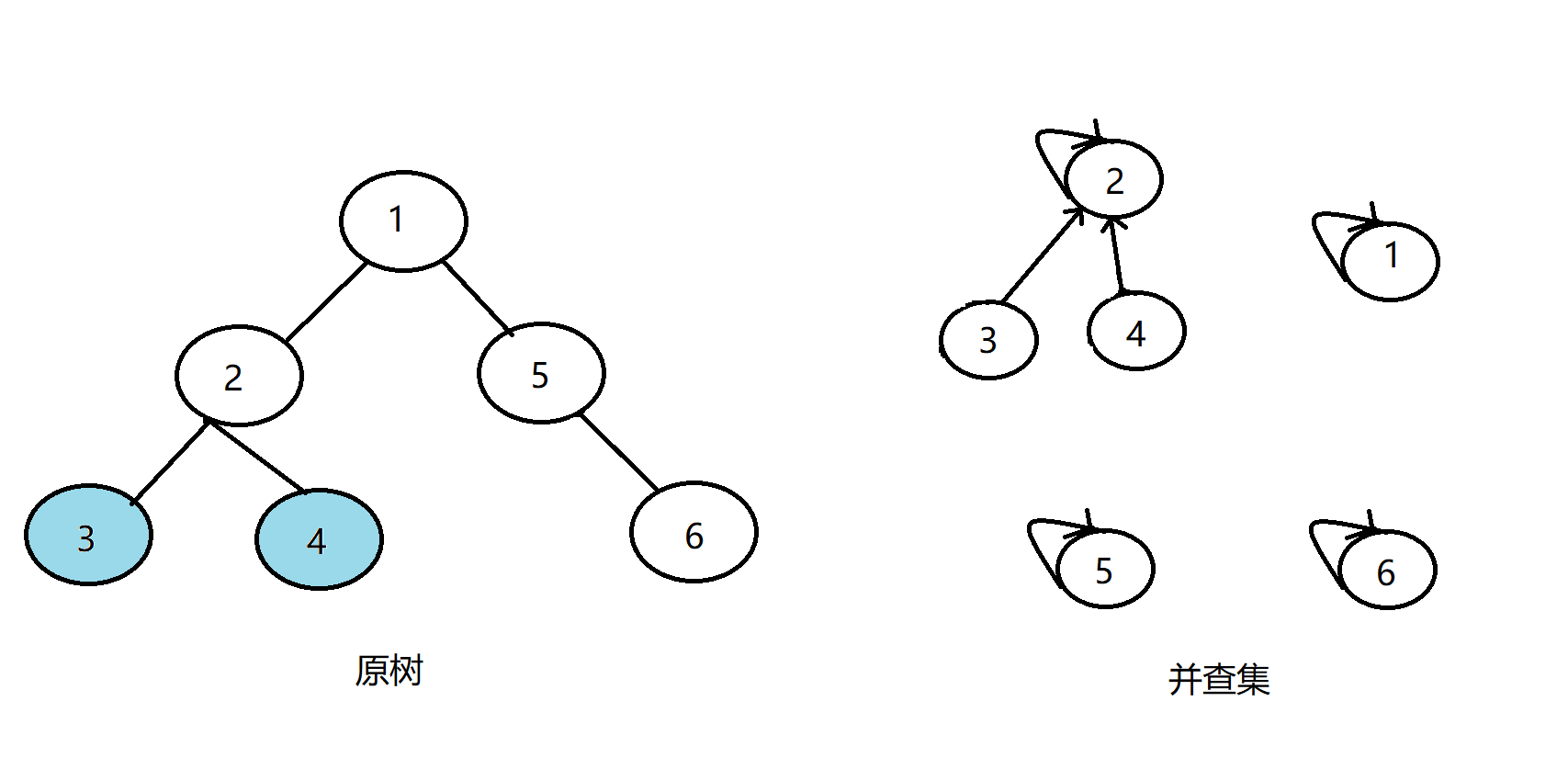
这时我们发现发现2没有未被搜完的子节点,寻找与其有关系的点;
发现5与2有关系,但vis[5]=0,即1还没被搜过,所以不操作;返回前一层搜索,将2的父亲节点设为1,更新vis[2]=1:

接着搜索1的另一个儿子节点5,继续搜5,发现5有一个子节点6;
搜索6,发现6没有子节点,则寻找与6有关系的点,发现4和6有关系;此时vis[4]=1,所以它们的最近公共祖先为4所在并查集的根节点——find(4)=1;(find(4)的顺序为f[4]=2-->f[2]=2-->f[1]=1 return 1;)
发现没有与6有关系的点了,返回此前一层搜索,把6在并查集中的的父亲节点设为5,更新vis[6]=1,表示6已经被搜完了:
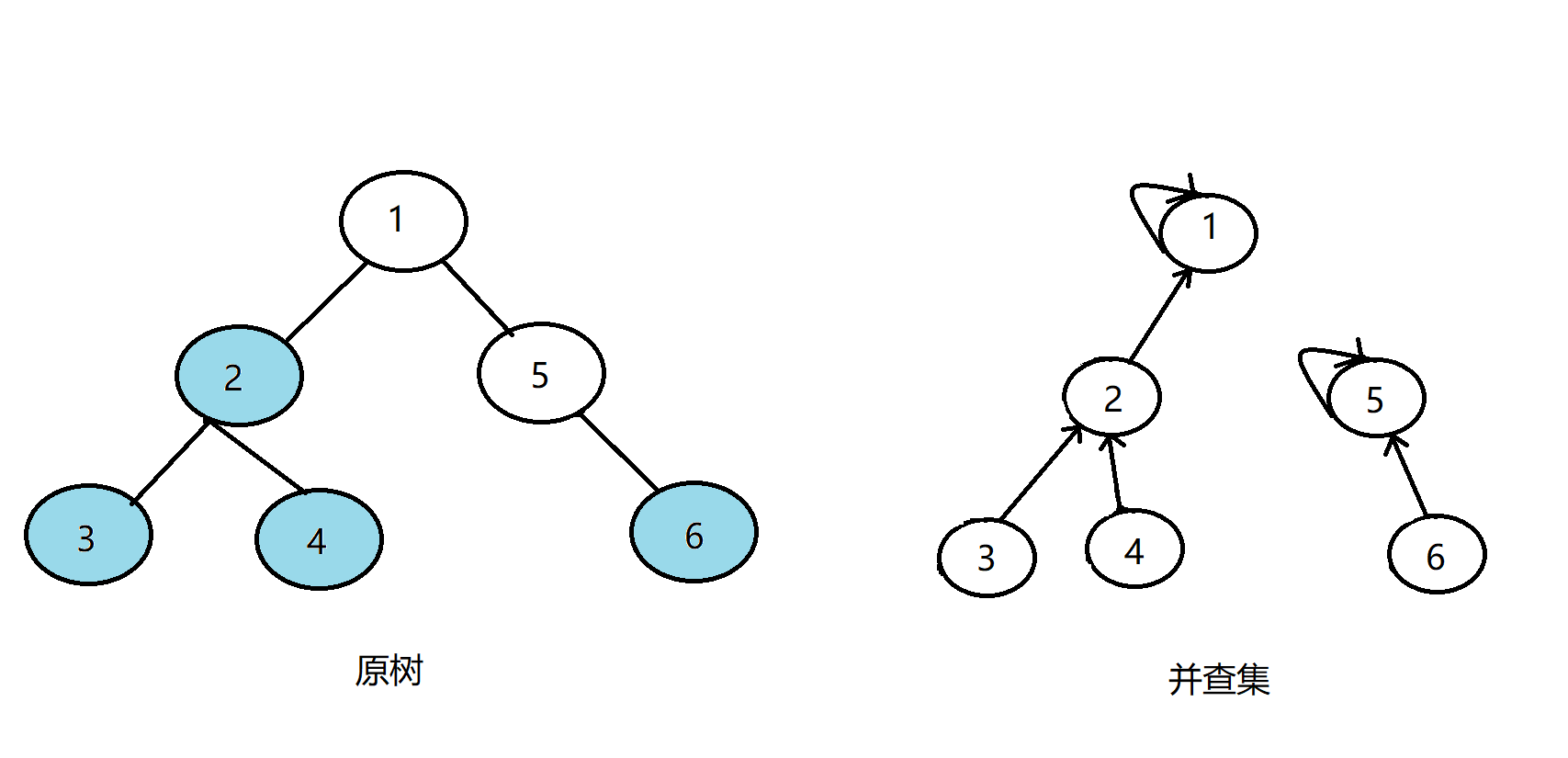
这时我们发现发现5没有没被搜过的子节点了,则寻找与5有关系的点;
发现2和5有关系,此时vis[2]=1,则它们的最近公共祖先为find(2)=1;(find(2)的顺序为f[2]=1-->f[1]=1 return 1;)
发现没有和5有关系的点了,返回此前一次搜索,把5在并查集中的的父亲节点设为1,更新vis[5]=1:
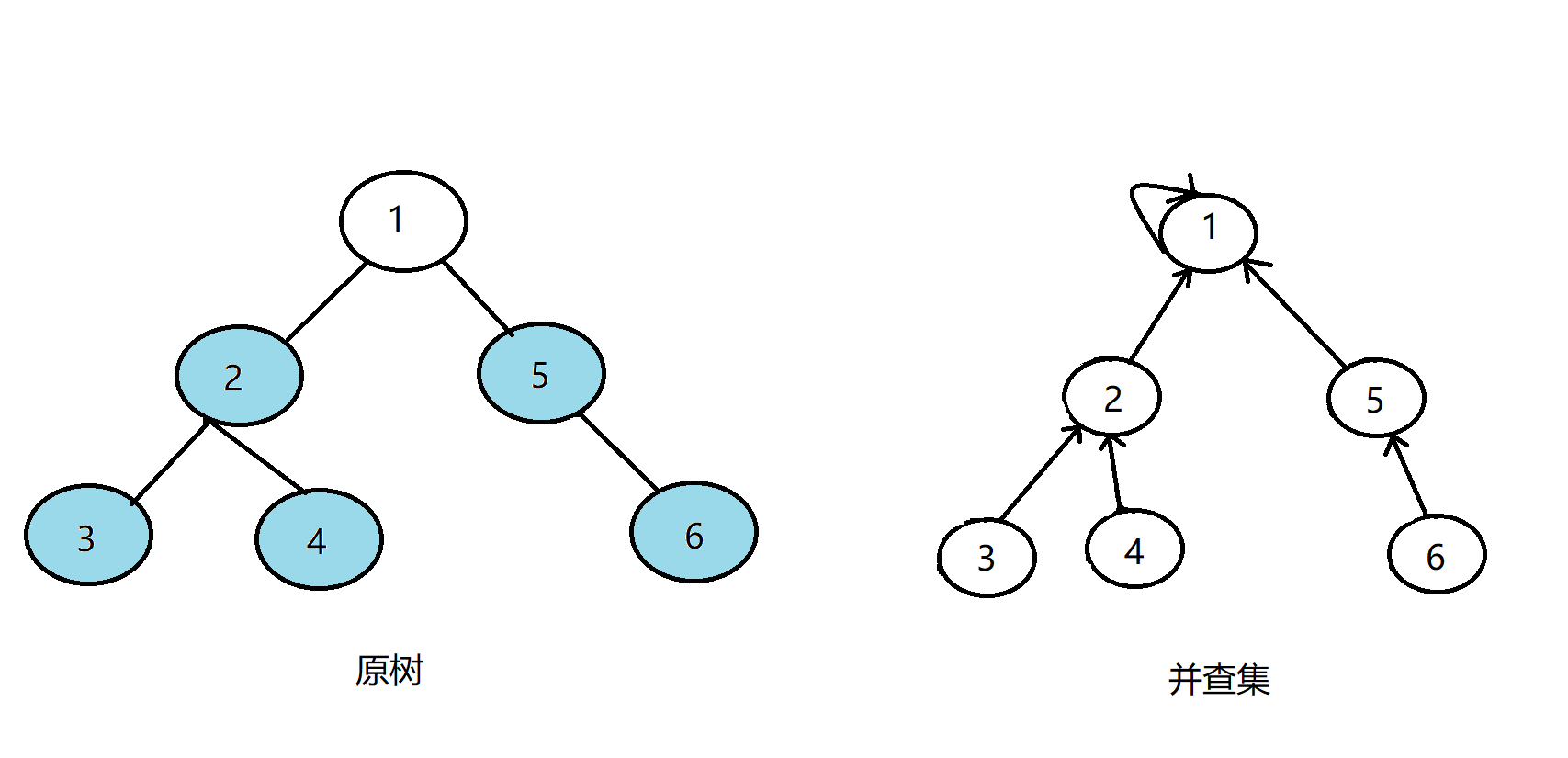
我们最后来看看1号节点,发现1没有没被搜过的子节点了,则寻找与1有关系的点;
发现3和1有关系,此时vis[3]=1,则它们的最近公共祖先为find(3)=1;(find(3)的顺序为f[3]=2-->f[2]=1-->f[1]=1 return 1;)
这时所有关系都处理完了,我们也求出了所有要求的LCA,Tarjan算法也就结束啦!
算法实现
Tarjan的代码实现其实非常简单,主要分为两个部分;
首先是DFS实现Tarjan的部分:
void tarjan(int f,int fath)//DFS实现tarjan
//f表示当前节点,fath表示它的父亲节点
{
for(int i=last[f];i;i=a[i].next)
if(a[i].y!=fath)
{
tarjan(a[i].y,f);//继续DFS
merge(f,a[i].y);//合并
vis[a[i].y]=1; //设置为访问过
}
//继续dfs其儿子节点
for(int i=lastt[f];i;i=b[i].next)
{//访问与f询问有关的点
if(vis[b[i].y]==1)//如果访问过
ans[b[i].num]=find(b[i].y);
}
}还有一部分是并查集部分:
void merge(int x,int y)
{
fa[y]=fa[x];//合并
}
int find(int x)//并查集上查找根节点
{
if(fa[x]!=x)fa[x]=find(fa[x]);//路径压缩
return(fa[x]);
}然后Tarjan的主体就基本写完了,还算是一种非常简洁的算法。在LCA中,如果不强制要求在线,还是建议写Tarjan的,不论是码量还是速度又有着无可匹敌的强大。
经典例题
[luoguP3379] 【模板】最近公共祖先(LCA)
题目描述
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。输入格式
第一行包含三个正整数N、M、S,分别表示树的结点个数、询问的个数和树根结点的序号。接下来N-1行每行包含两个正整数x、y,表示x结点和y结点之间有一条直接连接的边(数据保证可以构成树)。
接下来M行每行包含两个正整数a、b,表示询问a结点和b结点的最近公共祖先。
输出格式
输出包含M行,每行包含一个正整数,依次为每一个询问的结果。输入输出样例
输入 #1
5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5
输出 #1
4
4
1
4
4
说明/提示
时空限制:1000ms,128M数据规模:
对于30%的数据:N<=10,M<=10
对于70%的数据:N<=10000,M<=10000
对于100%的数据:N<=500000,M<=500000
又是刚刚那道题,直接贴上板子:
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
int x,y,next;
}a[2*500001];
int last[500001];
//邻接表存树
struct nodee
{
int x,y,next,num;
}b[2*500001];
//邻接表询问
int lastt[500001];
int vis[500001],fa[500001],ans[500001];
//vis[i]表示是否访问过
//fa[i]表示i在并查集上的父亲是谁
//ans[i]表示第i个询问的答案是多少
int tot,tott;
void add(int x,int y) //邻接表存树
{
tot++;
a[tot].x=x;a[tot].y=y;
a[tot].next=last[x];
last[x]=tot;
}
void addd(int x,int y,int num) //邻接表存询问
{
tott++;
b[tott].x=x;b[tott].y=y;
b[tott].next=lastt[x];
b[tott].num=num;
lastt[x]=tott;
}
void merge(int x,int y)
{
fa[y]=fa[x];//合并
}
int find(int x)//并查集上查找根节点
{
if(fa[x]!=x)fa[x]=find(fa[x]);//路径压缩
return(fa[x]);
}
void tarjan(int f,int fath)//DFS实现tarjan
//f表示当前节点,fath表示它的父亲节点
{
for(int i=last[f];i;i=a[i].next)
if(a[i].y!=fath)
{
tarjan(a[i].y,f);//继续DFS
merge(f,a[i].y);//合并
vis[a[i].y]=1; //设置为访问过
}
//继续dfs其儿子节点
for(int i=lastt[f];i;i=b[i].next)
{//访问与f询问有关的点
if(vis[b[i].y]==1)//如果访问过
ans[b[i].num]=find(b[i].y);
}
}
int n,m,s;
int main()
{
scanf("%d%d%d",&n,&m,&s);
for(int i=1;i<=n-1;i++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);//连边
}
for(int i=1;i<=n;i++)fa[i]=i;
//初始化将每个点在并查集上的父亲设为自己
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
addd(x,y,i);addd(y,x,i);
//离线处理
}
tarjan(s,0);//tarjan
for(int i=1;i<=m;i++)printf("%d\n",ans[i]);//输出答案
return 0;
}结语
通过这篇BLOG,相信你已经掌握了三种求解LCA的方法。其实在比赛中,裸的LCA并不常见,所以学会灵活运用才算是学会LCA算法的精髓,课后还要多加练习才能掌握其中的技巧和思想。最后希望你喜欢这篇BLOG!
Orz太强了,受益匪浅,涨了知识,以前孤陋寡闻的我只听说倍增和树剖的做法233
我爱上了欧拉序+ST表了,请问这个算法在功能和效率上能不能代替其他的LCA算法呢
QwQ当然是不行的啦,每种算法都有自己的优势,具体用哪种还是要看实际情况啦
但我觉得(不要你觉得#huaji)至少可以替代倍增?
然后就是,emmm。几个无伤大雅的特性,代码中不需要的ed数组可以去掉~
噢对,关于euler序的大小,如果你的算法是叶子节点只统计一次的,上限就是节点数x2(好像)。可以证明下做补充强调一下的,这个点有点小坑QWQ
当n很大但m很小的时候,因为预处理的常数,欧拉序的时间并没有倍增优秀QwQ ed的话可能在部分题目中用到比如可能还要同时查询子树大小?(在这里貌似用处不大);数组大小的话是的如果叶子只访问一次貌似接近2n,但是如果统计两次就是4n,怎么证明呢?对于每个点,其访问次数等于1+其儿子节点个数,所以euler序的大小就是 n+(n-1)=2n-1。