这几天刚刚重拾打程序的激情,还有些生疏啊……拜读了大佬的Blog后,突然想码一篇模拟退火。今天就让我们一同从爬山算法到模拟退火,走进神奇的玄学算法。
爬山算法
算法简介
爬山算法是local search(局部搜索)算法中最简单的一种。当我们遇到的问题的解空间很大时,我们想从中直接获取最优解是很耗时间的。但是,我们可以做到的是,我们可以从一个小的解空间短时间获得最优解,这就是local search算法的核心。
我们知道,一个全局最优解一定是局部最优解,但是一个局部最优解不一定是我们想要的全局最优解。若想得到真真切切的全局最优解,一种方法就是把所有局部最优解求解后取最优值。但是,前面提到的,在问题的解空间很大时,时间和空间可能都不允许我们这么做,所以这时我们就只能求解部分的局部最优解,在其中求得最优值,即一个比较优秀的解当成是全局的最优解。
而local search算法多种多样,其中,爬山算法是以local search为核心框架的启发式算法中最简单的算法。当然,结果一般也不太好,因为爬山算法有一个很大的缺点:不能跳出局部解。
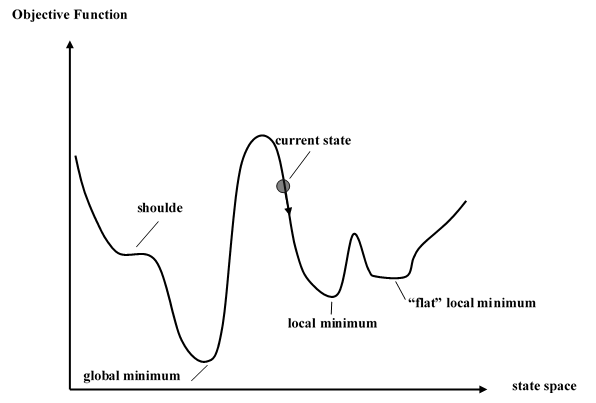
至于为什么爬山算法不能跳出局部解,是因为以local search为框架的启发式算法需要综合考虑到算法的两个方面,即intensification和diversification。Intensification为深度搜索,即尽可能找到局部最优解;(2)Diversification为广度搜索,即尽可能搜索到更多的解空间,以及避免陷入局部最优解。爬山算法在diversification这一方面没有任何措施,所以导致不能跳出局部最优解。
但是爬山算法作为local search算法中最简单的一种,思路简洁明了,有助于我们入门玄学算法。
算法过程
由于hill climbing-爬山算法是以local search为框架的,所以其算法过程也是很类似的。
首先,我们先摆出local search的过程:
(1) 生成初始解:算法从一个初始解或若干个初始解出发;
(2) 定义邻域和候选解:定义解的邻域,并产生若干个候选解;
(3) 确定新解:从候选解中确定新解;
(4) 迭代:重复上述搜索过程,直至满足终止条件,期间可能伴随着参数的调整。
再一一对应local search的过程,将其中一些元素具体化,即可得到hill climbing的过程:
(1) 生成初始解:算法从一个初始解开始。初始解可以随机生成,也可以是给定的。
(2) 定义领域和候选解:定义解的邻域和候选解。不同的爬山算法会考虑不同的邻域结构。
(3) 确定新解:选出候选解中的最优解,如果最优解大于当前解,则将该局部最优解作为新解;
(4) 迭代:重复上述搜索过程,直至满足终止条件。终止条件可以是时间、迭代次数,也可能是当前解不能进一步优化了。
代码实现
下面给出爬山算法的伪代码供大家参考:
Hill_Climbing algorithm for minimization problem
Procedure HillClimbing()
x:=getInitial(); //得到初始可行解X
while(the stopping condition is not reached)
x'=localSearch(N(x)); //从x的邻域中选择最优解作为x'
if(c'x'<=c'x)
x:=x'
else
return x
end这样我们的爬山算法就完成了,可以发现,酱紫的玄学算法还是有很大的局限性的,所以接下来我们救来学习一下更加高级的模拟退火算法。
模拟退火
算法简介
从百度百科的介绍我们可以知道:
模拟退火算法(Simulate Anneal,SA)是一种通用概率演算法,用来在一个大的搜寻空间内找寻命题的最优解。模拟退火是由S.Kirkpatrick, C.D.Gelatt和M.P.Vecchi在1983年所发明的。V.Černý在1985年也独立发明此演算法。模拟退火算法是解决TSP问题的有效方法之一。
模拟退火的出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法是一种通用的优化算法,其物理退火过程由加温过程、等温过程、冷却过程这三部分组成。
简而言之,模拟退火是一种玄学随机化算法。当一个问题的解空间很大,甚至是无穷时,而且不是一个单峰函数时,我们常使用模拟退火求解。
它与爬山算法最大的不同是,在寻找到一个局部最优解时,赋予了它一个跳出去的概率,而不是像爬山算法一样无法跳出局部最优解,从而使得模拟退火算法拥有更大的机会能找到全局最优解。
算法原理
说到模拟退火的原理,百度百科告诉我们:
模拟退火的原理也和金属退火的原理近似:将热力学的理论套用到统计学上,将搜寻空间内每一点想像成空气内的分子;分子的能量,就是它本身的动能;而搜寻空间内的每一点,也像空气分子一样带有“能量”,以表示该点对命题的合适程度。演算法先以搜寻空间内一个任意点作起始:每一步先选择一个“邻居”,然后再计算从现有位置到达“邻居”的概率。
金属退火指的是一种金属热处理工艺,指的是将金属缓慢加热到一定温度,保持足够时间,然后以适宜速度冷却。
而对应到OI上,就是在我们随机出一组解后,如果它比我们目前的最优解更优我们就接受它;反之,若它劣于我们目前得到的最优解,我们就以一个以当前温度和该组解与最优解的差相关的概率接受它。
具体来说,就是设当前这个新的解与最优解的差为 ΔE ,温度为 T , k 为一个随机数,那么接受这组解的概率为e^(ΔE/(T*k))。
算法过程
模拟退火算法大致由两个个部分组成,分别是随机生成新解和退火降温过程,下面就一一进行讲解。
生成新解
生成新解的过程通常分为三种情况,对应不同的套路,其中有:
坐标系内:随机生成一个点,或者生成一个向量。
序列问题:random_shuffle 或者随机交换两个数。
网格问题:可以看做二维序列,每次交换两个格子即可。
降温过程
在模拟退火过程中有三个参数,分别是初始温度 T0、降温系数 Δ 和终止温度 Tk。其中, T0 是一个比较大的数,Δ 是一个略小于 1 的正数,而 Tk 是一个略大于 0 的正数。
我们先让温度 T=T0,然后每次降温时 T'=T⋅Δ ,直到 T'≤Tk为止。
其大致过程如下(图片来源:维基百科):
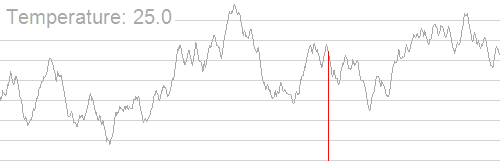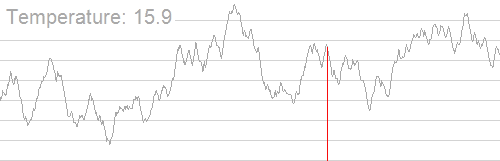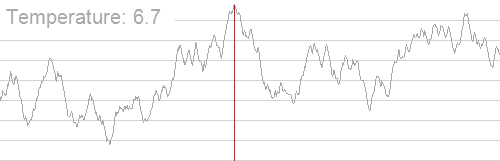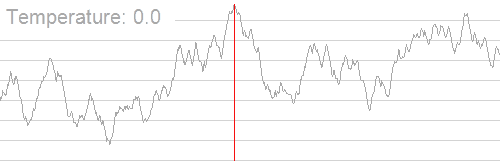
我们可以发现,随着温度的降低,我们得到的解也逐渐稳定下来,并逐渐集中在最优解附近。
注意事项
程序开始时,我们要先随机种子,也就是srand(一个常数)。这个常数可以决定分数。你可以使用233333,2147483647,10000000007等大质数。
因为模拟退火也是玄学的local search算法,所以一遍SA(模拟退火)往往无法跑出最优解,此时可以多跑几遍。
一个可行的方法是可以用一个全局变量记录所有跑过的SA的最优解,每次从那个最优解开始继续SA,可以减小误差。
至于时间复杂度 ,确实是O(玄学) 。
一般降温系数 Δ 与 1 的差减少一个数量级, 耗时大约多 10 倍;T0 和 Tk 变化一个数量级, 耗时却不会变化很大。
参数调试
在解题过程的调试中,我们经常会遇到得到的解不是最优解的情况,这时我们有多种方法可供选择:
1.调大 Δ 、调大 T0、调小 Tk,以及多跑几遍SA:
①当您的程序跑的比较快时,可以选择多跑几遍SA,或者调大 Δ ,从而增大得到最优解的概率。
②但如果原程序时间不理想的话,可以选择调大 T0 和调小 Tk ,这样做的话有可能进一步得到最优解且时间并不会增大太多。2.尝试更换随机数种子,或者 srand(rand()) ,总之,总有可能跑出正解。
3.别退火了,打正解吧QwQ
经典例题
下面就以一道经典例题为例,展示具体如何实现退火算法。
【luogu p1337】[JSOI2004]平衡点 / 吊打XXX
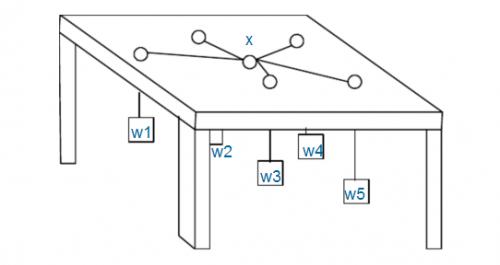
题目描述
如图:有n个重物,每个重物系在一条足够长的绳子上。每条绳子自上而下穿过桌面上的洞,然后系在一起。图中X处就是公共的绳结。假设绳子是完全弹性的(不会造成能量损失),桌子足够高(因而重物不会垂到地上),且忽略所有的摩擦。问绳结X最终平衡于何处。
注意:桌面上的洞都比绳结X小得多,所以即使某个重物特别重,绳结X也不可能穿过桌面上的洞掉下来,最多是卡在某个洞口处。
输入输出格式
输入格式:
文件的第一行为一个正整数n(1≤n≤1000),表示重物和洞的数目。接下来的n行,每行是3个整数:Xi.Yi.Wi,分别表示第i个洞的坐标以及第 i个重物的重量。(-10000≤x,y≤10000, 0<w≤1000)输出格式:
你的程序必须输出两个浮点数(保留小数点后三位),分别表示处于最终平衡状态时绳结X的横坐标和纵坐标。两个数以一个空格隔开。输入输出样例:
输入样例#1:
3
0 0 1
0 2 1
1 1 1输出样例#1:
0.577 1.000
显然,我们知道能量越小的状态越稳定,而在这个不存在动能的系统,势能就成了唯一存在的能量,所以我们自需要求出势能最小的点就可以啦,代码如下:
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
double x[1100],y[1100],w[1100];int n;
double xx,yy,xmax,ymax,xo,yo,wo,ans=1e18,js,t,delta,tk,now;
double value(double xx,double yy)
{
js=0;
for(int i=1;i<=n;i++)
js+=sqrt(((xx-x[i])*(xx-x[i])+(yy-y[i])*(yy-y[i])))*w[i];
return(js);
}//计算当前点的值
void sa()
{
xx=xmax;yy=ymax;
t=20000;delta=0.9988;tk=1e-14;//主要改这三个东西
while(t>tk)
{
double X=((rand()<<1)-RAND_MAX)*t+xx;
double Y=((rand()<<1)-RAND_MAX)*t+yy;
//生成新的点
now=value(X,Y);
double Delta=now-ans;
if(Delta<0)
{
xx=X;yy=Y;
ans=now;xmax=X;ymax=Y;
}//比当前解优-接受
else if (exp(-Delta/t)*RAND_MAX>rand()) xx=X,yy=Y;
//比当前解劣-以一定概率接受
t=t*delta;
}
}//模拟退火
void solve()
{
xmax=xo/(wo);ymax=yo/(wo);//从质心开始比较有优势
sa();sa();sa();sa();sa();
}//多跑几次就完事了
int main()
{
srand(233333333); srand(rand()); srand(rand()); srand(rand());
//玄学随机,好像搞越多次准确度越高……
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lf%lf%lf",&x[i],&y[i],&w[i]);
xo+=x[i]*w[i];yo+=y[i]*w[i];wo+=w[i];
}//读入
solve();
printf("%0.3lf %0.3lf",xmax,ymax);
return 0;
}PS退火的参数真的特别玄学,我我我交了块两页才过QwQ
进阶退火
当然模拟退火算法不是万能的,在某些特定情况下,需要一些更加骚的操作,比如退火套其他算法。
比如用的比较多的分块退火,在下图所示的情况下函数的峰特别多,所以我们要用分块模拟退火的做法。
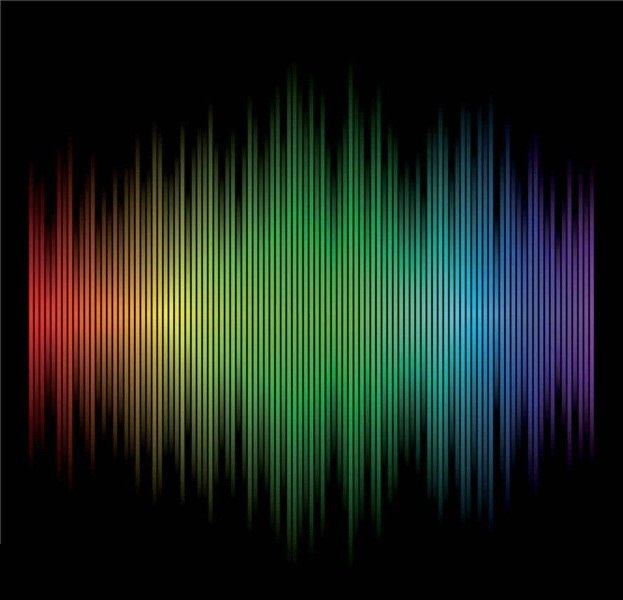
其大致算法是:将其分为几块,然后对每块跑一遍SA,最后再合并答案。
特别需要注意的是这里块的数量不是√n,而是一个比较小的数。此时我们要灵活判断,根据不同的题用不同的大小。
对时间的控制
我们知道,多次跑模拟退火虽然得到正解的概率更大,但是在传统竞赛中,时间不能超,所以这时我们就可以使用clock() 函数,返回程序运行时间。
具体酱紫做就可以了:
while ((double)clock()/CLOCKS_PER_SEC<MAX_TIME) SA();
其中MAX_TIME是一个自定义的略小于1的正数,可以根据喜好取0.7~0.8。
结语
通过这篇BLOG,相信你已经对神奇的玄学算法有所了解了。貌似什么求最优解的题都可以用模拟退火搞一搞,但是要记住,退火不是你的首选而是没其他办法下的无奈之举。最后希望你喜欢这篇Blog!