由于准备高考的缘故大半年没更新了呀……最近搞完自主招生终于可以慢慢补档了。最近通过大佬的BLOG初略地复习了一下这两种排序。今天,就让我们一同从桶排序到基数排序,走进神奇的排序算法吧!
初级-桶排序
一说到排序算法,可能不少同学都会第一时间喊出"我大快排天下第一!"其实不然。我们知道快排这种基于比价的排序算法时间复杂度下限是 O(n log n) 。至于为什么,我们可以简单地将其理解为给定序列的排列方式有 n! 种,然后我们每次进行一次比较最多可以排除掉一半的序列,最后复杂度相当于 O(log(n!)),由斯特林公式我们可以求得复杂度=O(log(n!))=O(n log n)。
这时如果我们需要一个O(n)级别的排序算法,有没有可能实现呢?答案是肯定的——桶排序应运而生,其复杂度为O(n+max{val[i]}),下面就先介绍一下单关键字的桶排序。
实现原理
桶排序的实现原理特别简单,就是将元素依次放入容器中,然后按顺序依次扫描元素,得到各个元素的排名,下面举个栗子:
假如我们有四个元素需要从小到大排序,他们分别是4,1,5,3:
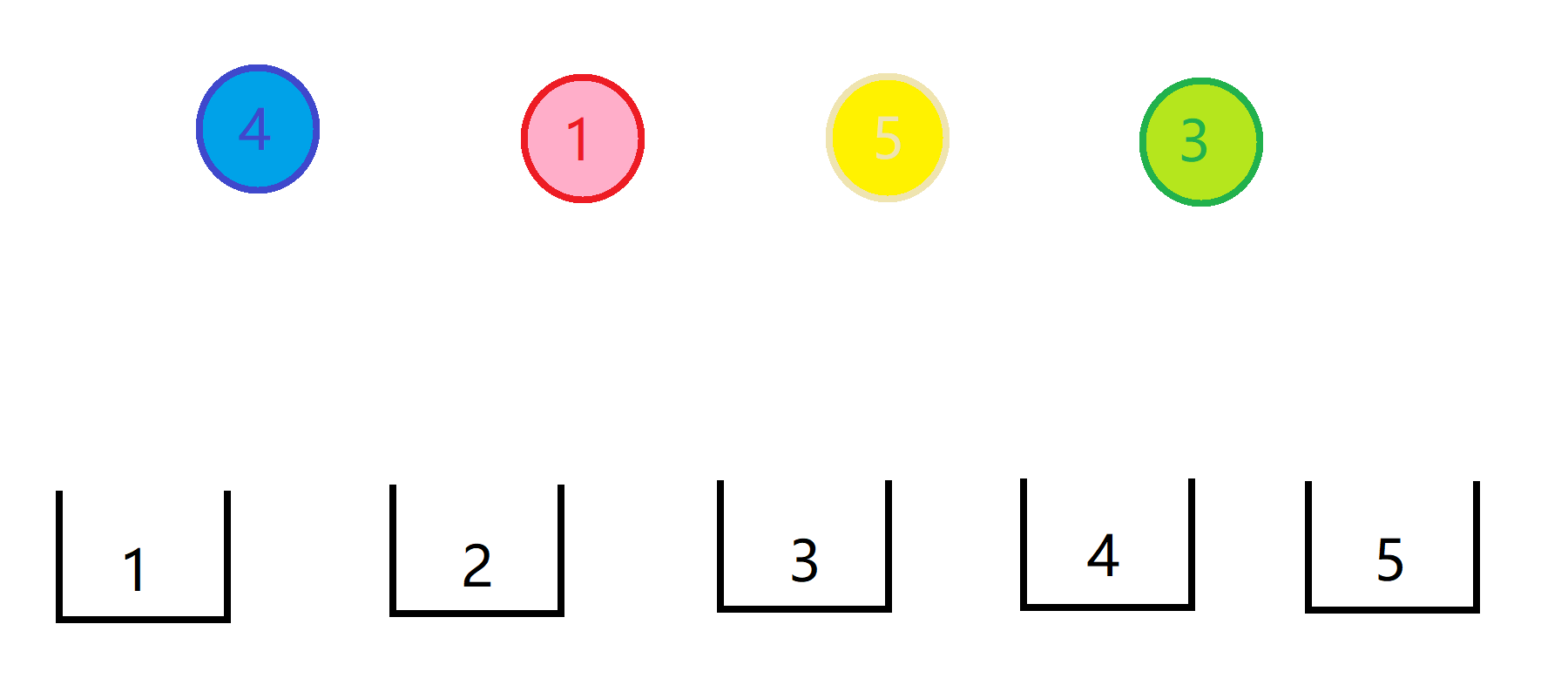
接着我们把元素丢到对应值的容器里:
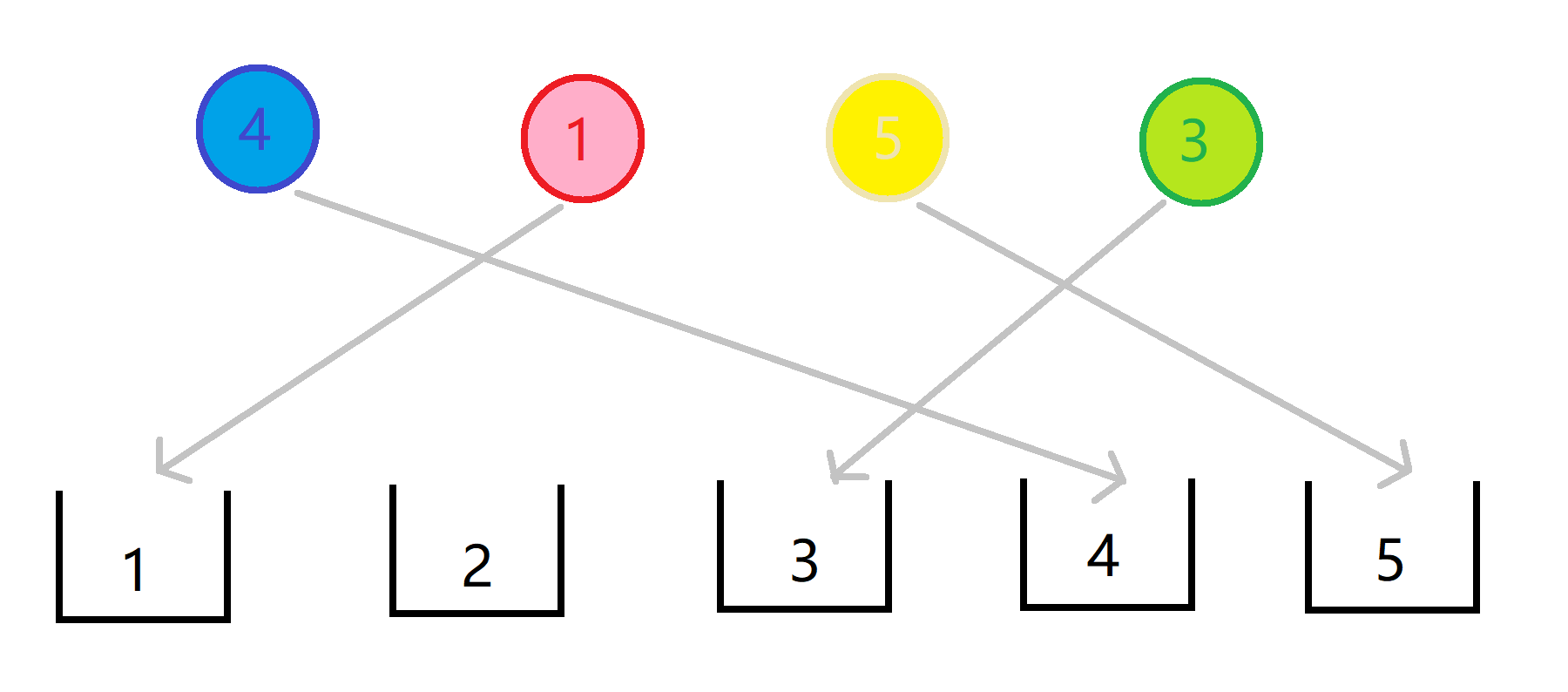
最后我们按从小到大的顺序扫描容器,得出各个元素的排名及各元素从小到大的排序了:
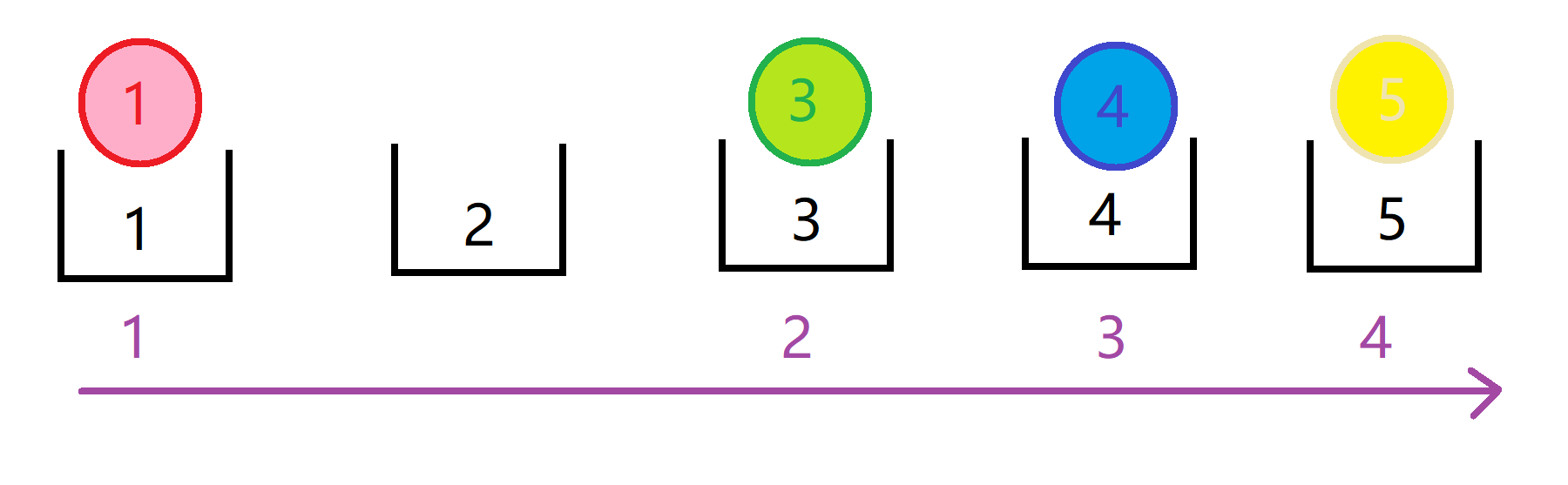
这样,我们就在O(n+max{val[i]})的时间复杂度下完成了桶排序。
具体代码
下面就以最简单的从小到大排序作为例子,桶排序具体代码如下:
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
const int Maxn=11000;//定义元素中最大数为Maxn
int a[Maxn];//开一个大小为Maxn的容器
int i,j,k,m,n,o,p,js,jl,x;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&x);
a[x]++;
}//读入数据,并将其放入容器里
for(int i=1;i<Maxn;i++)
while(a[i]>0)
{
a[i]--;
printf("%d ",i);
}//按顺序访问容器,输出其中的元素
return 0;
//完成排序
}进阶-基数排序
我们通过对桶排序的学习可以发现,桶排序如果遇上元素最大值Maxn比较大的数据,就会爆时间和空间,无法继续胜任了,那如果还是想要O(n)级别的排序算法怎么办呢?这时基数排序就站了出来。
实现原理
基数排序可以理解为是多关键字的桶排序,n为数字可以理解为n个关键字。也就是把最高位当作第一关键字,次高位当成第二关键字……以此类推,进行桶排序。那么关键字的桶排序要如何排序呢?
其实基数排序的重要思想就是从最后一个关键字进行桶排序,然后再按最后一个关键字排序顺序依次对倒数第二个关键字进行桶排序……依次类推,当完成第一关键字的排序后,基数排序就完成了。什么不是很明白?没事,下面以对两位数,也就是双关键字从小到大排序为例,进行讲解:
现在我们有A0=32,45,99,17,27,05,02,13六个数需要排序,首先我们按先对每个数的个位,也就是第二关键字进行桶排序,丢入对应的容器中:

排序后得到A1=32, 02, 13,45,05,27,99:

接着按A1的顺序,对各个元素的十位也就是第一关键字进行桶排序,丢入对应的容器中:
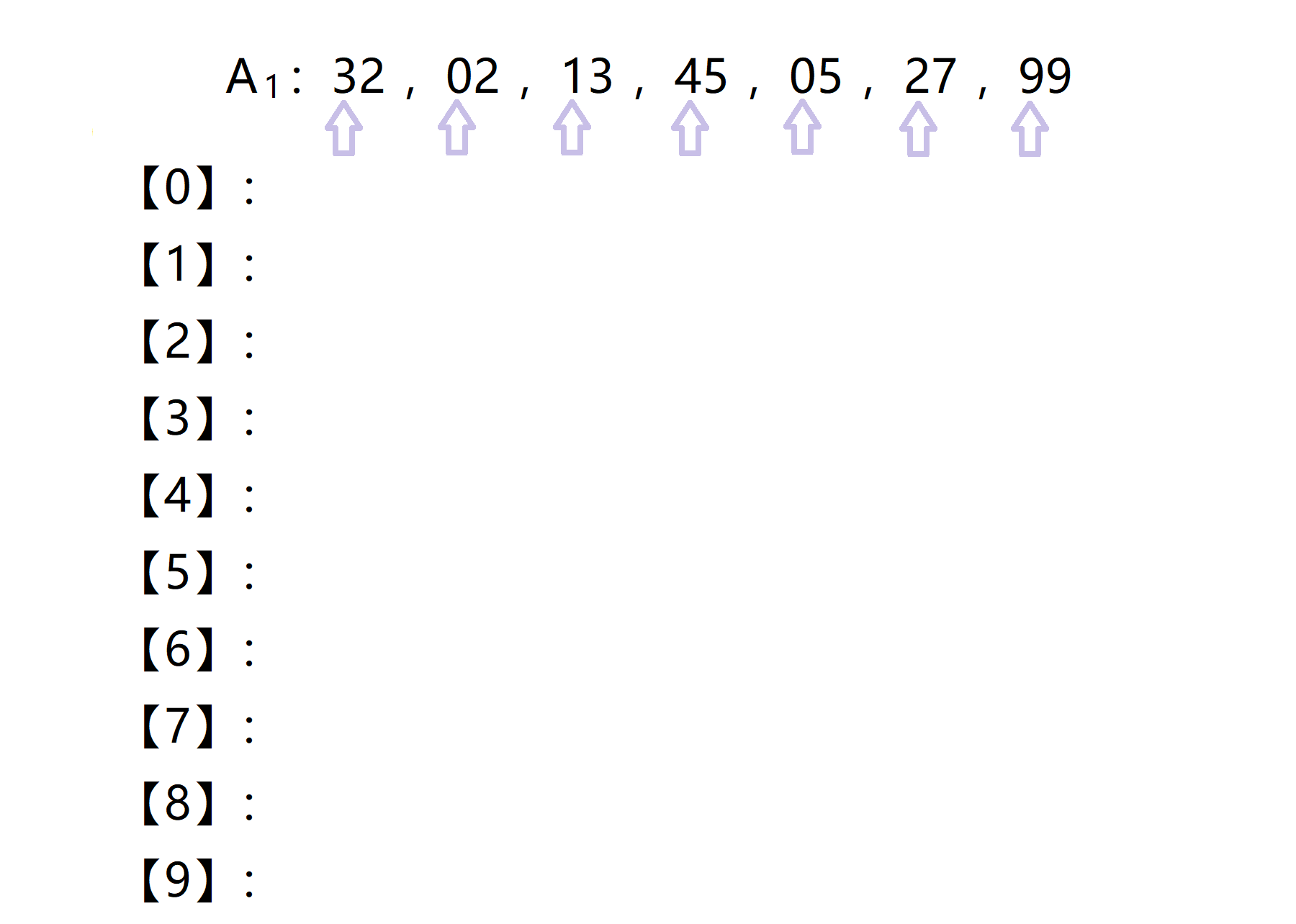
得到排序后的A2=02,05,13,27,32,45,99,此时所有关键字都进行了一次排序,基数排序结束,A2即为A0排序后的序列:

是不是很方便快捷呢?
具体代码
就以一道快排的模板题作为例子,展示一下从小到大进行基数排序的具体代码:
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
int v[11];
void print()
{
int pd=10;
for(int i=1;i<=10;i++)
if(v[i]>0)
{
pd=i;
break;
}
for(int i=pd;i<=10;i++)printf("%d",v[i]);
printf(" ");
}
}a[110000];//将数字按位拆开
int n,m,o;int id[110000],rk[110000],sum[11];
//id[i]表示第k+1号到n号关键字排好后第i个数据的原本编号
//rk[i]表示原本编号为i的数据在进行完k号关键字的技术排序后的排名
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&m);id[i]=i;
for(int j=10;j>=1;j--)
{
o=m%10;m=m/10;
a[i].v[j]=o;
}
}
//读入数据,把整数拆成10个关键字排序,每个关键字的值域都是[0,9],记录初始id
int *x=id,*y=rk;//因为要交换数组,据说用指针就是O(1)的了
for(int key=10;key>=1;key--)
{
memset(sum,0,sizeof(sum));
for(int i=1;i<=n;i++)sum[a[i].v[key]]++;
for(int i=1;i<=9;i++)sum[i]+=sum[i-1];//对第k关键字进行桶排序
for(int i=n;i>=1;i--)y[sum[a[x[i]].v[key]]--]=x[i];
//y[i]记录排名第i的元素序号,记住不要把a[x[i]]写成a[i]了,x[i]是上一关键字排好后的顺序
for(int i=1;i<=n;i++)x[y[i]]=i;
//x[i]记录i号元素的排名
swap(x,y);//交换
}
for(int i=1;i<=n;i++)a[x[i]].print();//输出
return 0;
}优化的基数排序
实现原理
我们发现正常的基数排序也就是上面操作用的时间复杂度为 (n + log10 (Max{m})) (log10 (Max{m})),可以简写为 O(nlogr m),其中 n 为元素个数, r 是排序所用的基数, m 为所有元素最大值的大小。但是一般的 logr m接近10,而且还涉及到取模等各种操作,导致整体的常熟比较大,速度略慢。
所以我们考虑一下能不能进行优化?一说到常数的优化,二进制总是少不了的。我们可以以二的幂次为基数的排序,这样的话几乎所有操作都可以围绕二进制操作,常数小,然后再一个就是如果以 2^8=256为一个基数的话,那么int范围内的 logr m也只有4的大小,然后据说255的数组还可能可以写入内存而不是硬盘(也有可能写入缓存)。
于是我们发现以二的幂次为基数的二进制基数排序是我们所需要的,而且效果也比较优秀。
下面我们就通过一个例子来深入理解一下酱紫做的原理吧!
我们现在有四个数要从小到大进行排序,我们以四位为一个关键字,即对于这些八位二进制数,我们后四位为第二关键字,前四位为第一关键字进行排序:
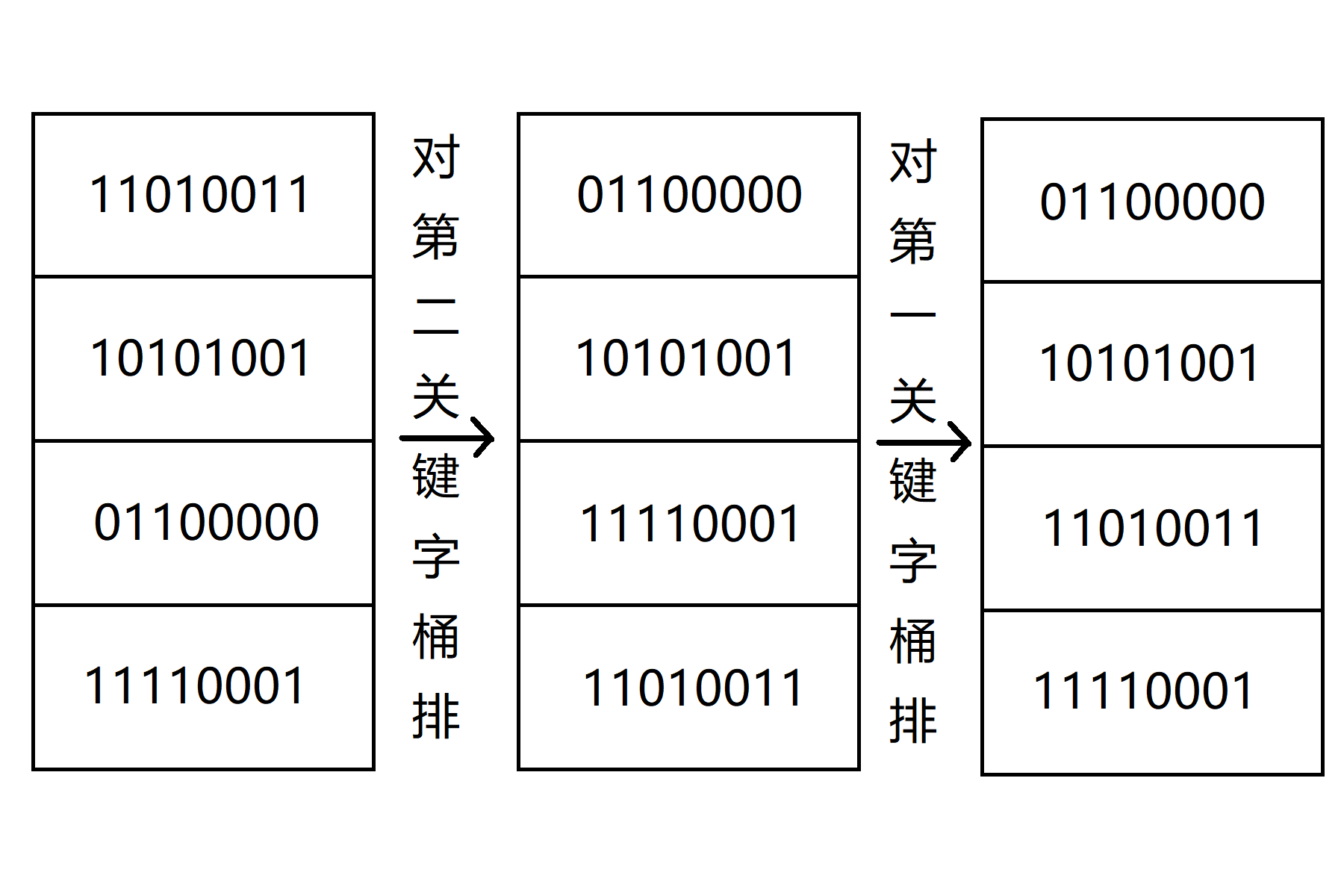
具体代码
还是以这快排的模板题作为例子,展示一下从小到大进行优化后基数排序的具体代码【此版本为未用二进制优化的中间版本,加上二进制优化的大杀器版本见下一板块】实际测试下来可以比普通的基数排序快一半左右:
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
short v[6];
void print()
{
int pd=10,js=0,jl=1;
for(int i=1;i<=4;i++)
if(v[i]>0)
{
pd=i;
break;
}
for(int i=4;i>=pd;i--)
{
js+=jl*v[i];
jl*=256;
}
printf("%d ",js);
}
}a[110000];//将数字按位拆开
int n,m,o;int id[110000],rk[110000],sum[256];
//id[i]表示第k+1号到n号关键字排好后第i个数据的原本编号
//rk[i]表示原本编号为i的数据在进行完k号关键字的计数排序后的排名
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&m);id[i]=i;
for(int j=4;j>=1;j--)
{
o=m%256;m=m/256;//以256为基数进行优化
a[i].v[j]=o;
}
}
int *x=id,*y=rk;//因为要交换数组,据说用指针就是O(1)的了
for(int key=4;key>=1;key--)
{
memset(sum,0,sizeof(sum));
for(int i=1;i<=n;i++)sum[a[i].v[key]]++;
for(int i=1;i<=256;i++)sum[i]+=sum[i-1];//对第k关键字进行桶排序
for(int i=n;i>=1;i--)y[sum[a[x[i]].v[key]]--]=x[i];
//y[i]记录排名第i的元素序号,记住不要把a[x[i]]写成a[i]了,x[i]是上一关键字排好后的顺序
for(int i=1;i<=n;i++)x[y[i]]=i;
//x[i]记录i号元素的排名
swap(x,y);//交换
}
for(int i=1;i<=n;i++)a[x[i]].print();//输出
return 0;
}拓展的基数排序
实现原理
我们有时候还会有一个对于结构体进行多关键字排序的需求,我们注意到C++内定的数据类型至少为1个字节,一般用的整数为4个字节。然后我们发现对于一个32位的整数 k ,我们对k进行32为的比较其实可以认为是先进行16位高位的比较然后再进行16位的低位的比较,在高位相等的时候比较低位,这不就是双关键字排序吗?
所以结构体的双关键字排序可以这样做:先利用指针类型转换结构体成为32/64位整数,然后再适当调整基数直接排序这些整数,然后就可以得到这些排序后的结构体。
结构体的内存分布如下:

对于这个结构体,我们只需要使用64位的基数排序,基数 2^16就可以解决了,代码和上面的类似【当然可以二进制优化】,过程也是首先开四个数组作为4个关键字的容器(基数为 2^16,然后把元素用二进制运算拆开,放入容器内,接着对容器进行桶排序;最后利用上一次排序的结果交替利用数组进行下一次排序,如此循环就完成了。
具体代码
继续以这道快排的模板题作为例子下面展示二进制优化下的代码,实测下来比不用二进制优化又可以优化30%左右的时间:
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int a[110000],b[110000],r1[257],r2[257],r3[257],r4[257];
int n,m,o;int sum[256];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&m);a[i]=m;
r1[m & 0xff]++;//二进制取低8位
r2[(m >> 8) & 0xff]++;//二进制取16位
r3[(m >> 16) & 0xff]++;//二进制取24位
r4[(m >> 24) & 0xff]++;//二进制取32位
}
for(int i=1;i<=256;i++)
{
r1[i]+=r1[i-1];
r2[i]+=r2[i-1];
r3[i]+=r3[i-1];
r4[i]+=r4[i-1];
}//累加
for(int i=n;i>=1;i--)b[r1[a[i] & 0xff]--]=a[i];
for(int i=n;i>=1;i--)a[r2[(b[i] >> 8) & 0xff]--]=b[i];
for(int i=n;i>=1;i--)b[r3[(a[i] >> 16) & 0xff]--]=a[i];
for(int i=n;i>=1;i--)a[r4[(b[i] >> 24) & 0xff]--]=b[i];
//基数排序
for(int i=1;i<=n;i++)printf("%d ",a[i]);//输出
return 0;
}结语
通过这篇Blog相信你已经彻底理解桶排序和基数排序的精髓了,顺带一提,其实基数排序也是可以对浮点数进行排序的哦,这要感谢IEEE 754的标准,它制定的浮点标准还带有一个特性:如果不考虑符号位(浮点数是按照类似于原码使用一个bit表示符号位s,s = 1表示负数),那么同符号浮点数的比较可以等价于无符号整数的比较,方法就是先做一次基数排序,然后再调整正负数部分顺序即可。感兴趣的同学可以自行摸索。最后希望你喜欢这篇Blog!
我看哭了,你们呢
别别别,好好学别哭