第一次出模拟题很紧张啊……大部分都有原题，但是背景故事测试数据自定义比较器之类的什么的都是我苦苦冥想出来的QwQ。最后说一句，出题目真的好累啊，下面就让我们一起看DAY2的题目吧。

T1 取走木薯（bring)

题目部分

【问题描述】

上回书说到，我们的蒟蒻勇者凭借他过人的智慧赢得木薯魔王设下的蒟蒻棋，而魔王 也非常守信用地将他抢来的所有木薯还给了蒟蒻勇者，并由我们的蒟蒻勇者充当快递员的 身份将它们全部带回坚果国分发给受难的农夫们。 但是在取走木薯之前，我们的蒟蒻勇者必须要清点一下木薯的数量，如果每个木薯都 是完整的就好了，但是木薯魔王常常在晚上打完 CJ(Code-Jvruo)后偷偷的吃几口库存的 木薯，所有有些木薯并不完整，而是原来木薯的几分之几。 为了方便统计，我们的蒟蒻勇者想知道—— 如果给定整数 a(a≤10^10000) 和 b(b≤10^10000),那么 a/b mod 998244353 的值是多少？
　　

【输入格式】

从文件 bring.in 中读入数据。
输入一共两行。 第一行，一个整数 a。第二行，一个整数 b。

【输出格式】

输出到文件 bring.out 中。
输出一个整数，代表求余后的结果。如果无解，输出QwQ

【样例 1 输入】

233
666

【样例 1 输出】

18595654

解题思路

这道题作为 DAY2 的签到题当然也是非常简单的啦。这题出的是分数取模的裸题，只 要知道费马小定理或者扩展欧几里得就能很轻易的 AC 了。下面就来具体讲解一下吧，分 析题目，发现要求的值即为 a*b^-1，然后有两种解法：

一、费马小定理（【标程写法】）：

对于本题而言，a 为整数，且除数为质数(p= 998244353)，因此可以使用费马小定理，
即 a^(p-1)≡1(mod p)，然后得出 c=a∗b^(-1)≡a∗b^(p−2)(mod p)，接下来用快速幂求 a*b^(p-2)%p 即可。特别的，当 b=0 时，即分母为 0，因此无解，输出 QwQ。本算法的优 势是较容易写，但除数必须是质数，因而通用性不强。

二、扩展欧几里得 :

解析题目发现：本题就是求 b 在 mod p 的意义下的逆元。求 a 的逆元相当于求解 ax=1(mod p)，这个方程可以转化为 ax-my=1，然后直接套用扩欧求解 x,y。特别的，当 gcd(a,p)≠1 时，方程无解，因此 a 也无逆元。

到这里这道题就做完啦！难度定在提高。

程序实现

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
char sa[110000],sb[110000];
long long a,b,aa,bb,i,j,k,m,n,o,p,js,jl,la,lb;

long long ksm(long long n)
{
    if(n==0)return(1);
    if(n==1)return(bb);

    if(n%2==0)
    {
        js=ksm(n/2)%998244353;
        jl=js*js%998244353;
        return(jl);
    }
    else
    {
        js=ksm(n/2)%998244353;
        jl=js*js%998244353;
        jl=jl*bb%998244353;
        return(jl);
    }

}
int main()
{
    FILE *fin,*fout;
    fin=fopen("bring.in","rb");
    fout=fopen("bring.out","wb");
    fscanf(fin,"%s",sa+1);la=strlen(sa+1);
    fscanf(fin,"%s",sb+1);lb=strlen(sb+1);

    aa=0;bb=0;
    for(int i=1;i<=la;i++)aa=(aa*10+sa[i]-'0')%998244353;
    for(int i=1;i<=lb;i++)bb=(bb*10+sb[i]-'0')%998244353;

    if(bb==0)
    {
        fprintf(fout,"QwQ");
        fclose(fin);
        fclose(fout);
        exit(0);
    }

    a=aa;
    b=ksm(998244351);

    fprintf(fout,"%lld",a*b%998244353);

    fclose(fin);
    fclose(fout);

    return 0;
}

T2 吃掉木薯（eat)

题目部分

【问题描述】

在计算完木薯的数量后，我们的蒟蒻勇者带着几十车木薯——我们的战利品大摇大摆 地向坚果国走去。“我要把它们全部分给受难的农夫们，”蒟蒻勇者想，“但这样……对 我们农夫有什么好处吗？带回去也是要被当成赋税被国王掠夺走的，不如我……” 确实，在这个世界里，木薯是最富有魔力的食物，吃下一斤木薯就能让人学会释放火 球术，坚果国国王因此强迫农夫们定期上交木薯作为赋税。那么如果一口气吃下十几车的 木薯的话……结果不堪设想！ 所以我们的蒟蒻勇者决定了，他要吃下所有的木薯，用自己的能力建立一个理想的国 度——一个充满《荒野大坚果Ⅱ》的国度！但是摆在面前的是一个更加现实的问题，每个 木薯上都有一些数字，但是因为下雨潮湿，一些数字变得模糊了，只能认得清某一些木薯 上的数字是一样的，只能用一些字母来表示。要获得木薯的魔力，就一定要解出每个字母 所代表的数字是多少？蒟蒻勇者想了想，打电话给了正在做模拟题的你——
为了求解每个字母所代表的数字，我们给出你关于这些字母的加法算式。这里的加法 是 N 进制加法，算式中三个数都有 N 位，允许有前导的 0。 由于我们只知道哪些数字是相同的，我们将相同的数字用相同的字母表示，不同的数 字用不同的字母表示。如果这个算式是 N 进制的，我们就取英文字母表午的前 N 个大写字 母来表示这个算式中的 0 到 N-1 这 N 个不同的数字：但是这 N 个字母并不一定顺序地代表 0 到 N-1。输入数据保证 N 个字母分别至少出现一次。
来看一个简单的例子：

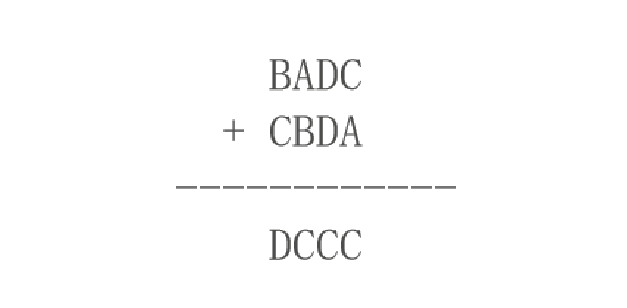
上面的算式是一个 4 进制的算式。很显然，我们只要让 ABCD 分别代表 0123，便可以 让这个式子成立了。你的任务是，对于给定的 N 进制加法算式，求出 N 个不同的字母分别 代表的数字，使得该加法算式成立。输入数据保证有且仅有一组解。

【输入格式】

从文件 eat.in 中读入数据。
输入包含四行。 第一行有一个正整数 N(N≤26)。 后面的三行，每行有一个由大写字母组成的字符串，分别代表两个加数以及和。这 3 个字符串左右两端都没有空格，从高位到低位，并且恰好有 N 位。

【输出格式】

输出到文件 eat.out 中。
输出仅有一行，即唯一的那组解。
解是这样表示的：输出 N 个数字，分别表示 A,B,C,…所代表的数字，相邻的两个数字 用一个空格隔开，不能有多余的空格。

【样例 1 输入】

5
ABCED
BDACE
EBBAA

【样例 1 输出】

1 0 3 4 2

解题思路

这题也是一道考验选手码力的题目。搜索加剪枝就可以啦。下面讲两个剪枝的技巧— —首先每当我们一列填完以后，就验证一下可不可行，虽然这看起来好像会增加很多无谓 的计算，但实际上这会大大剪去无用状态；接着是对于每个字母代表数字的枚举，从大往 小的枚举比从大到小的枚举要块挺多的，恐怕这就是玄学吧。加上这两个剪枝以后就能顺 利 AC 啦。

难度定在提高。

程序实现

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
FILE *fin,*fout;
char s[4][110];
int flag[330]={0},used[330]={0};
int i,j,k,m,n,o,p,js,jl,jw,t,w1,w2,w3;

int id(char c)
{
    return(c-'A'+1);
}

int find(int x,int y,int t)
{
    if(x==0)
    {
        if(t==0)
        {
            for(int i=1;i<=n;i++)fprintf(fout,"%d ",flag[i]);
            exit(0);
        }
        return 0;
    }

    for(int i=x-1;i>=1;i--)
    {
        w1=flag[id(s[1][i])];
        w2=flag[id(s[2][i])];
        w3=flag[id(s[3][i])];

        if(w1!=-1 && w2!=-1 && w3!=-1)if((w1+w2)%n!=w3 && (w1+w2+1)%n!=w3)return 0;
    }

    if(flag[id(s[y][x])]==-1)
    {
        for(int i=n-1;i>=0;i--)
        if(used[i]==0)
        {
            if(y<3)
            {
                flag[id(s[y][x])]=i;
                used[i]=1;
                find(x,y+1,t);
                flag[id(s[y][x])]=-1;
                used[i]=0;
            }
            else
            {
                int w=flag[id(s[1][x])]+flag[id(s[2][x])]+t;
                if(w%n!=i)continue;

                flag[id(s[y][x])]=i;
                used[i]=1;
                find(x-1,1,w/n);
                flag[id(s[y][x])]=-1;
                used[i]=0;
            }
        }
    }
    else
    {
        if(y<3)find(x,y+1,t);
        else
        {
            int w=flag[id(s[1][x])]+flag[id(s[2][x])]+t;
            if(w%n!=flag[id(s[y][x])])return 0;
            find(x-1,1,w/n);
        }
    }
}
int main()
{
    FILE *fin,*fout;
    fin=fopen("eat.in","rb");
    fout=fopen("eat.out","wb");
    fscanf(fin,"%d",&n);
    for(int i=1;i<=3;i++)fscanf(fin,"%s",s[i]+1);
    t=0;memset(flag,-1,sizeof(flag));
    find(n,1,0);
    return 0;
}

T3 构筑炮台（battery)

题目部分

【问题描述】

我们的蒟蒻勇者终于吃下了全部的木薯，他决定在坚果国的城墙外构筑一片 炮台阵地。我们可以把蒟蒻的阵地假象成 N*M 的矩阵，现在要在这个阵地上安置 若干个炮台。由于技术限制，要求任意三个炮台不能在同一行也不能在同一列上， 那么我们的蒟蒻勇者一共有多少种放置炮台的方法呢？

【输入格式】

从文件 battery.in 中读入数据。
第一行包含两个整数 N(N≤100)，M(M≤100)，表示矩阵的长和宽，之间由一个空格隔开。

【输出格式】

输出到文件 battery.out中。
第一行一个整数，表示总共的方案数，由于该值可能很大，只需给出方案数 模 9999973 的结果。

【样例 1 输入】

1 3

【样例 1 输出】

7

解题思路

这是一道很经典的 DP 题，一上来看 100%的数据肯定是很蒙的，所以我们可以根据数 据一步一步慢慢猜测出最终的解法。 首先，30%的算法，没什么好说的，就是单纯的暴力，将每种情况搞出来，判断可行 性，时间复杂度 O(2^(n*n))。 然后我们重点来思考一下 50%的解法，N,M 至少有一个数不超过 8，这很明显是在暗 示我们使用状压 DP，我们考虑可以用一个三进制数 k 表示前 i 列的状态，比如当 k=01201 时，就代表此时第一列还没有放炮，第二列已经放了一个炮，第三列已经放了一 个炮了，第四列还没有放炮，第五列已经放了一个炮了。所以我们可以设 a[i][k]为第 i 行状 态为 k 的方案总数，然后正常的状压 DP 转移就可以了，还是挺简单的，50 分到手。 现在我们考虑 100%的解法，显然，我们 DP 的方向但应该是对的，但是为什么刚刚 50%的做法过不了 100%呢？那是因为表示状态的 k 这一维实在太大了。所以我们就考虑， 能不能把 k 给简化或者替代掉？当然可以，其实在 DP 转移的过程中，哪一列是有一个 炮，哪一列有两个炮其实是不重要的，主要是要知道有几列有一个炮，有几列有两个炮。
所以我们就设 a[i][j][k] 为前 i 行，有 j 列有一个炮，k 列有两个炮【当然就有（m-jk）列没有炮】的方案总数，接着我们分情况讨论转移就解决了。

难度定在提高+/省选，不过有思路的话还是很简单的。

程序实现

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
long long a[110][110][110];
long long i,j,k,m,n,o,p,js,jl,jk;
int main()
{
    FILE *fin,*fout;
    fin=fopen("battery.in","rb");
    fout=fopen("battery.out","wb");
    fscanf(fin,"%lld%lld",&n,&m);
    a[0][0][0]=1;

    for(int i=0;i<n;i++)
    for(int j=0;j<=m;j++)
    for(int k=0;k<=m-j;k++)
    {
        a[i+1][j][k]=(a[i+1][j][k]+a[i][j][k])%9999973;//直接转移

        //这一行不放炮

        if(j+k<m)a[i+1][j+1][k]=(a[i+1][j+1][k]+(m-j-k)*a[i][j][k])%9999973;//把一个没有炮的列变成有一个炮的列
        if(j>0)a[i+1][j-1][k+1]=(a[i+1][j-1][k+1]+j*a[i][j][k])%9999973;//把一个有一个炮的列变成一个有两个炮的列

        //这一行放一个炮

        if(j+k<m-1)a[i+1][j+2][k]=(a[i+1][j+2][k]+(m-j-k)*(m-j-k-1)/2*a[i][j][k])%9999973;//把两个没有炮的列变成两个只有一个炮的列
        if(j>1)a[i+1][j-2][k+2]=(a[i+1][j-2][k+2]+j*(j-1)/2*a[i][j][k])%9999973;//把两个只有一个炮的列变成两个有两个炮的列
        if(j+k<m)if(j>0)a[i+1][j][k+1]=(a[i+1][j][k+1]+(m-j-k)*j*a[i][j][k])%9999973;//把一个没有炮的列变成有一个炮的列，同时把之前一个只有一个炮的列变成有两个炮的列

        //这一行放两个炮

    }
    js=0;
    for(int i=0;i<=m;i++)
    for(int j=0;j<=m-i;j++)
    js=(js+a[n][i][j])%9999973;
    //统计结果总数
    fprintf(fout,"%lld",js);
    fclose(fin);
    fclose(fout);
    return 0; 
} 

T4 蒟蒻国王（king)

题目部分

【问题描述】

经过几年的奋战，蒟蒻勇者终于推翻了坚果国王的统治，建成了蒟蒻主义国 家，除去了木薯赋税，得到了农夫们的拥护。 现在蒟蒻国王想知道还有多久《荒野大坚果Ⅲ》才能发售。我们知道，发售 的时间的计算公式形如 a^b，现在给出你 a 和 b，还有多久《荒野大坚果Ⅲ》才 能发售。由于时间可能很长，所以答案对 m 取模。 换句话说，给你三个正整数，a,b, m ； 你需要求：a^b mod m 。

【输入格式】

从文件 king.in 中读入数据。
输入一行一行三个整数，a,m,b。

【输出格式】

输出到文件 king.out中。
一个整数表示答案。

【样例 1 输入】

2 7 4

【样例 1 输出】

2

【样例2输入】

998244353 12345 98765472103312450233333333333

【样例2输出】

5333

解题思路

这道题作为 DAY1 的压轴题看起来是一道裸的快速幂，但当你定睛一看数据范围，是要用欧拉定理的。下面我就来讲解一下吧！

{欧拉定理}

结论: φ(n) 表示小于等于 n 的正整数中与 n 互质的数的个数（欧拉函数）。 a 与 m 互质时，a^φ(m)≡1 mod m

{拓展欧拉定理}

扩展欧拉定理无需 a,m 互质。 结论：

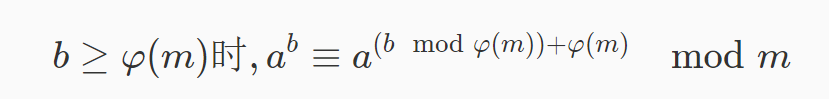
有了这两个结论这道题就很简单了，直接读入然后套拓展欧拉定理就可以啦。至于 φ(n)的求解，就直接从 2-sqrt（n）枚举就行了。这道题到这里就结束啦。

难度定在提高+/省选。

程序实现

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
long long n,m,p,a,b,fi,lb,bb,aa,ans,jl,js,temp;
char sb[24000000];

long long ksm(long long n)
{
    if(n==0)return(1);
    if(n==1)return(a);

    if(n%2==0)
    {
        js=ksm(n/2)%m;
        jl=js*js%m;
        return(jl);
    }
    else
    {
        js=ksm(n/2)%m;
        jl=js*js%m;
        jl=jl*a%m;
        return(jl);
    }

}

int main()
{
    FILE *fin,*fout;
    fin=fopen("king.in","rb");
    fout=fopen("king.out","wb");
    fscanf(fin,"%lld%lld",&a,&m);
    fscanf(fin,"%s",sb+1);lb=strlen(sb+1);
    fi=m;temp=m;

    for(int i=2;i<=int(sqrt(m));i++)
    {
        if(temp%i==0)
        {
            fi=fi/i*(i-1);
            while(temp%i==0)temp=temp/i;
        }
    }
    if(temp>1)fi=fi/temp*(temp-1);

    b=0;

    if(lb>=7)
    {
        for(int i=1;i<=lb;i++)b=(b*10+sb[i]-'0')%fi;
        b=b+fi;
    }
    else
        for(int i=1;i<=lb;i++)b=b*10+sb[i]-'0';

    ans=ksm(b);

    fprintf(fout,"%lld",ans);
    fclose(fin);
    fclose(fout);

    return 0;
}

结语

以上是 JROI DAY2 的题目和解析了，第一届JROI也到这里结束了。希望你能在这次模拟题中有所收获。最后希望你喜欢这篇BLOG！