在现如今的OI比赛中，越来越多的出现一些偏向于MO的题目(但大多只需要猜想结论，不需要证明)，所以这篇BLOG，就让我们一起学一些经典的MO题目吧【第一次用surface不是很熟练可能手写出来比较丑望谅解】！

不等式的证明

常见的不等式

（一）均值不等式

1.png

（二）柯西不等式

2.png

然后很多同学问柯西不等式怎么证明啊？其实很简单，利用构造二次函数的方法可以了，下面给出我手写的证明(字比较丑QwQ)：

3.png

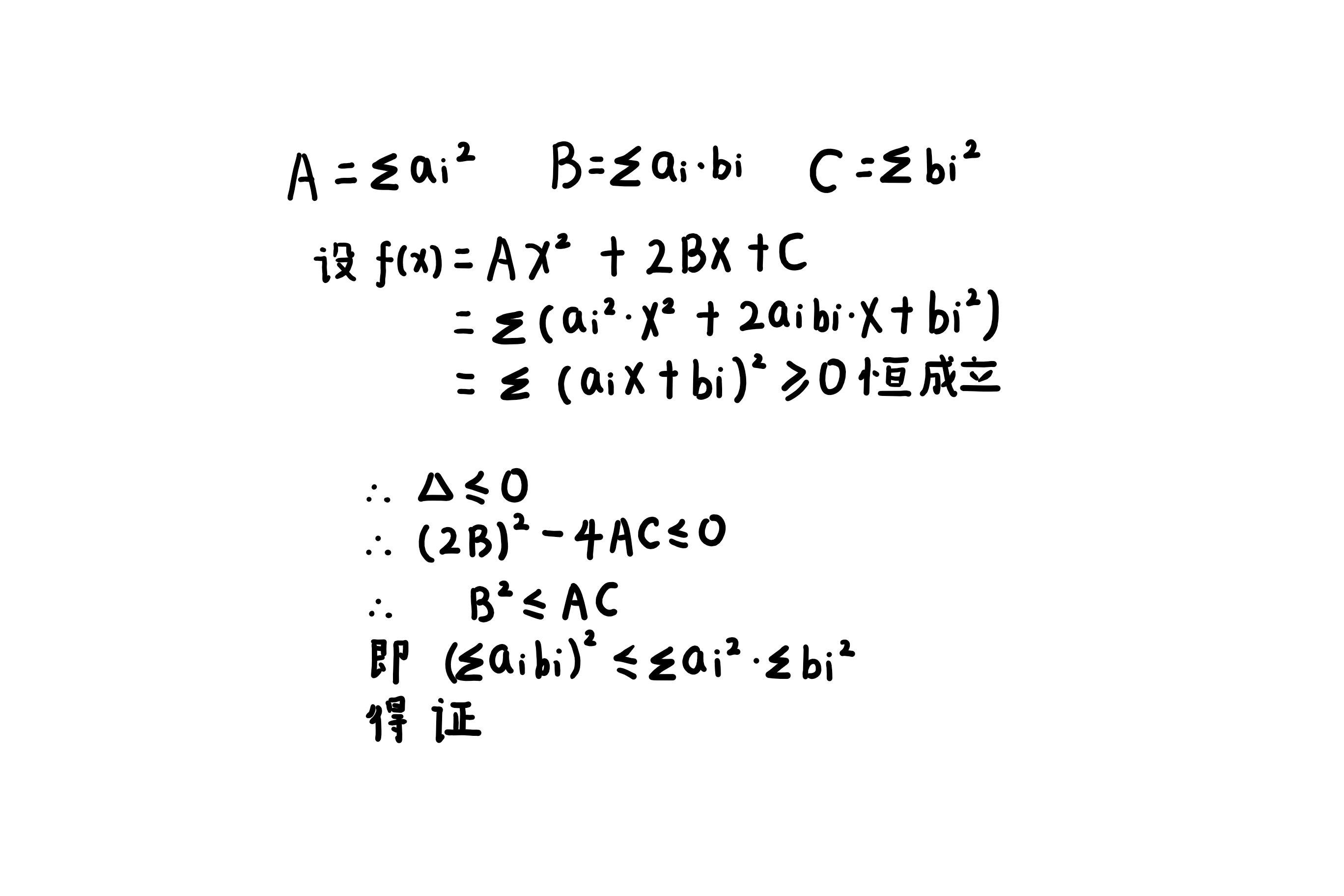
（三）其他经典不等式

还有其他许多很经典的不等式，在这里就不一一讲解了，感兴趣的同学可以自行了解，其主要有：

绝对值 (Absolute Value) 不等式
排序 (Sequence) 不等式
卡尔松 (Carlson) 不等式
琴生 (Jensen) 不等式
闵科夫斯基 (Minkowski) 不等式
伯努利 (Bernoulli) 不等式
权方和不等式———赫尔德 (Hölder) 不等式

经典例题

Q1.1

4.png

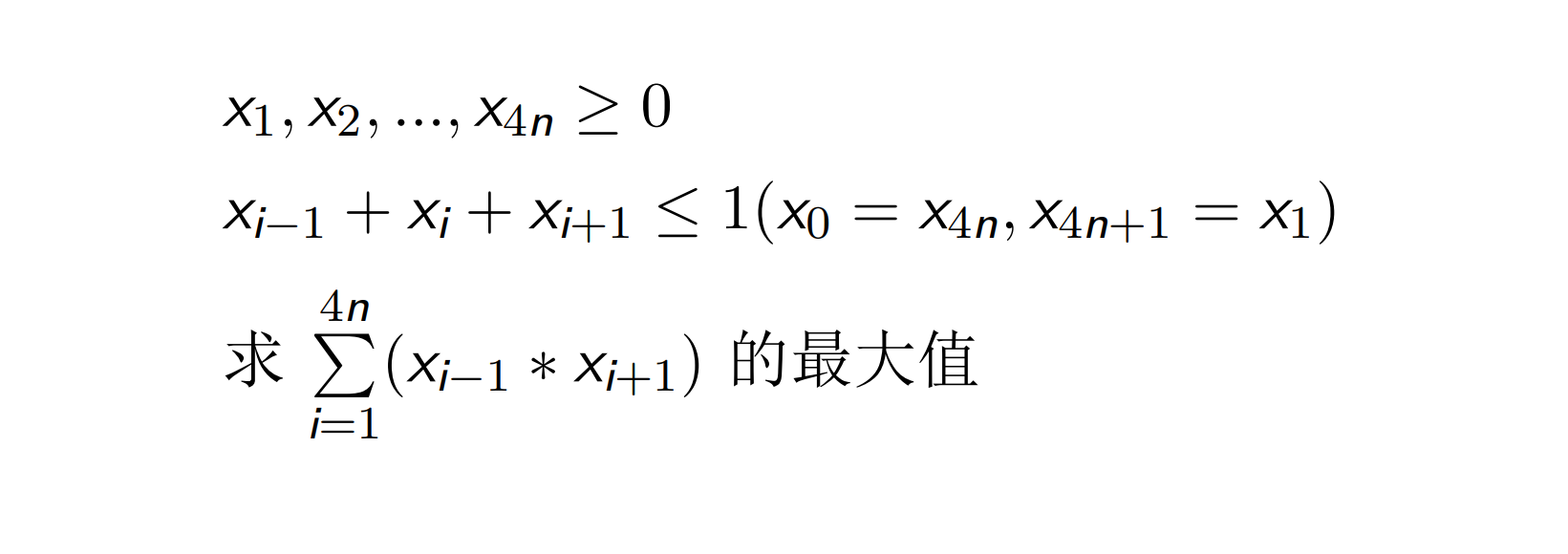
首先，作为一个合格的OIer，我们应该能猜的出答案，没错，当原式子最大时，x的序列为0，1/2间隔，即x的序列大概长这样：0 1/2 0 1/2 0 1/2 0 1/2 ……0 1/2，所以我们的答案就应该为n/2。但是如果证明呢？我们考虑先分析前四个数，然后把结论推广到整个数列，所以证明如下：

6.png

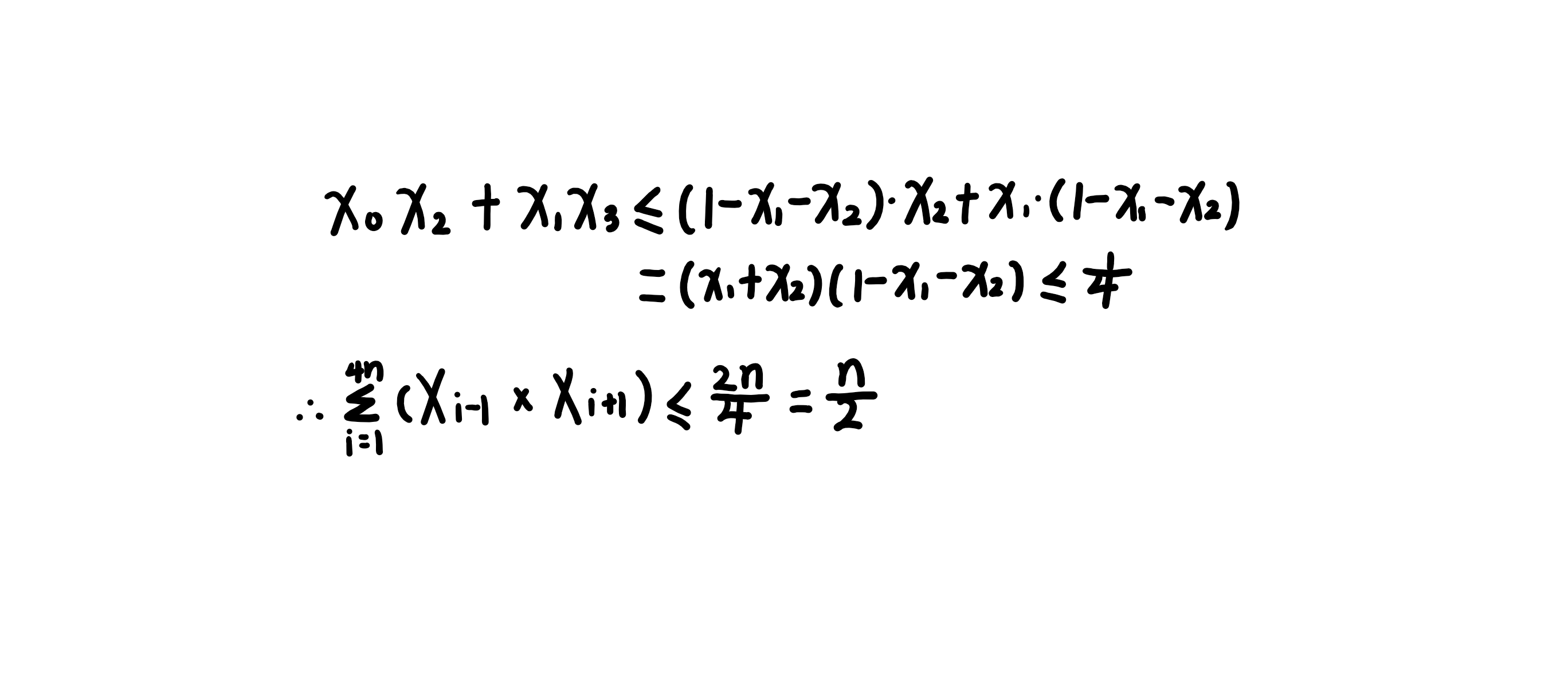
Q1.2

5.png

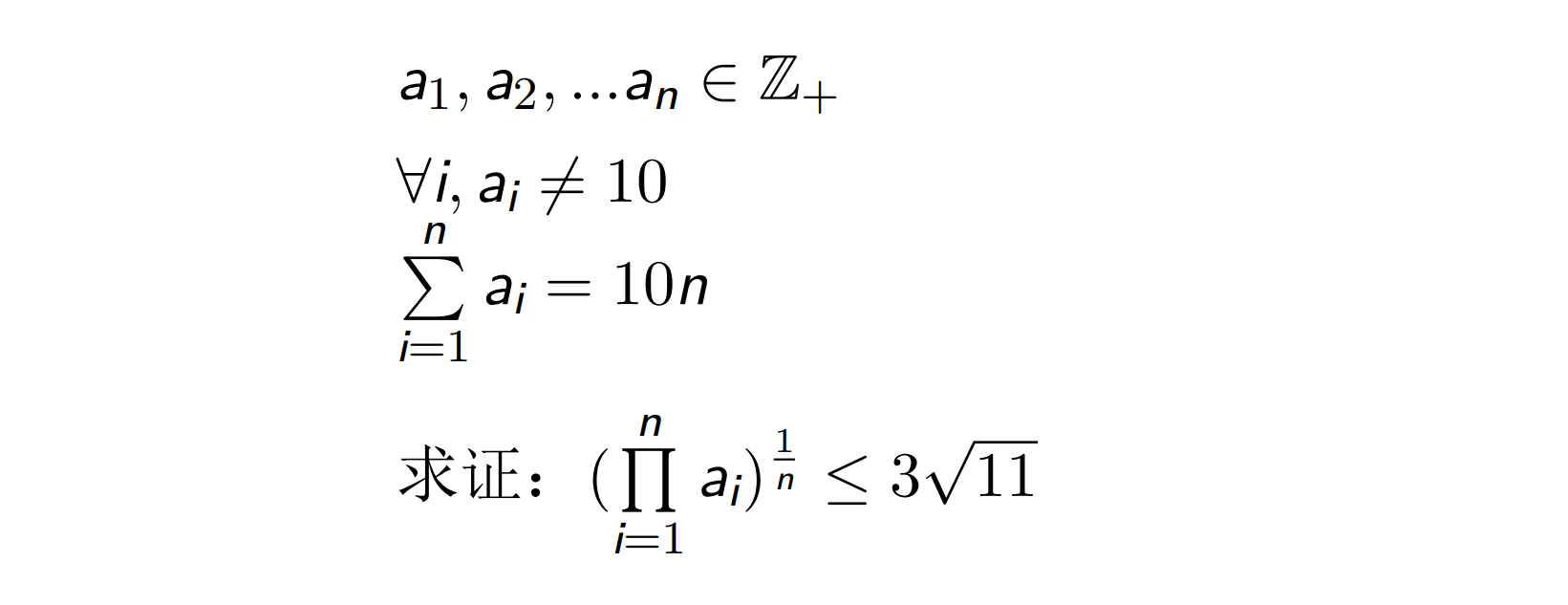
证明如下：

7.png

当然会有同学问了，那n为奇数的情况呢？那就更取不到完整的m个(9.11)了，所以答案会更小，所以我们的结论是对的。

多项式相关

常见多项式定理

威尔逊定理

8.png

经典例题

Q2.1

9.png

证明如下：

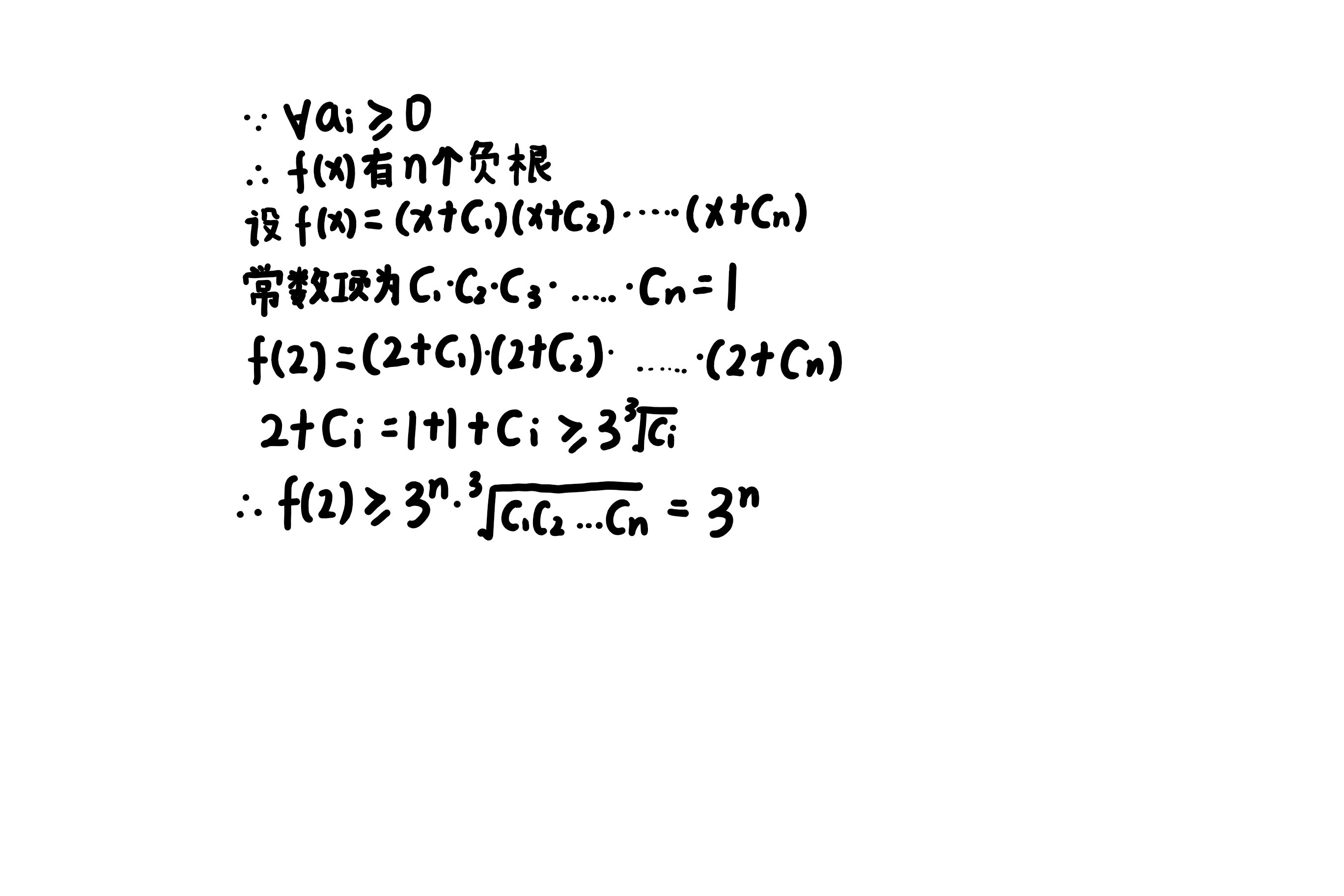
11.png

Q2.2

10.png

求解过程如下：

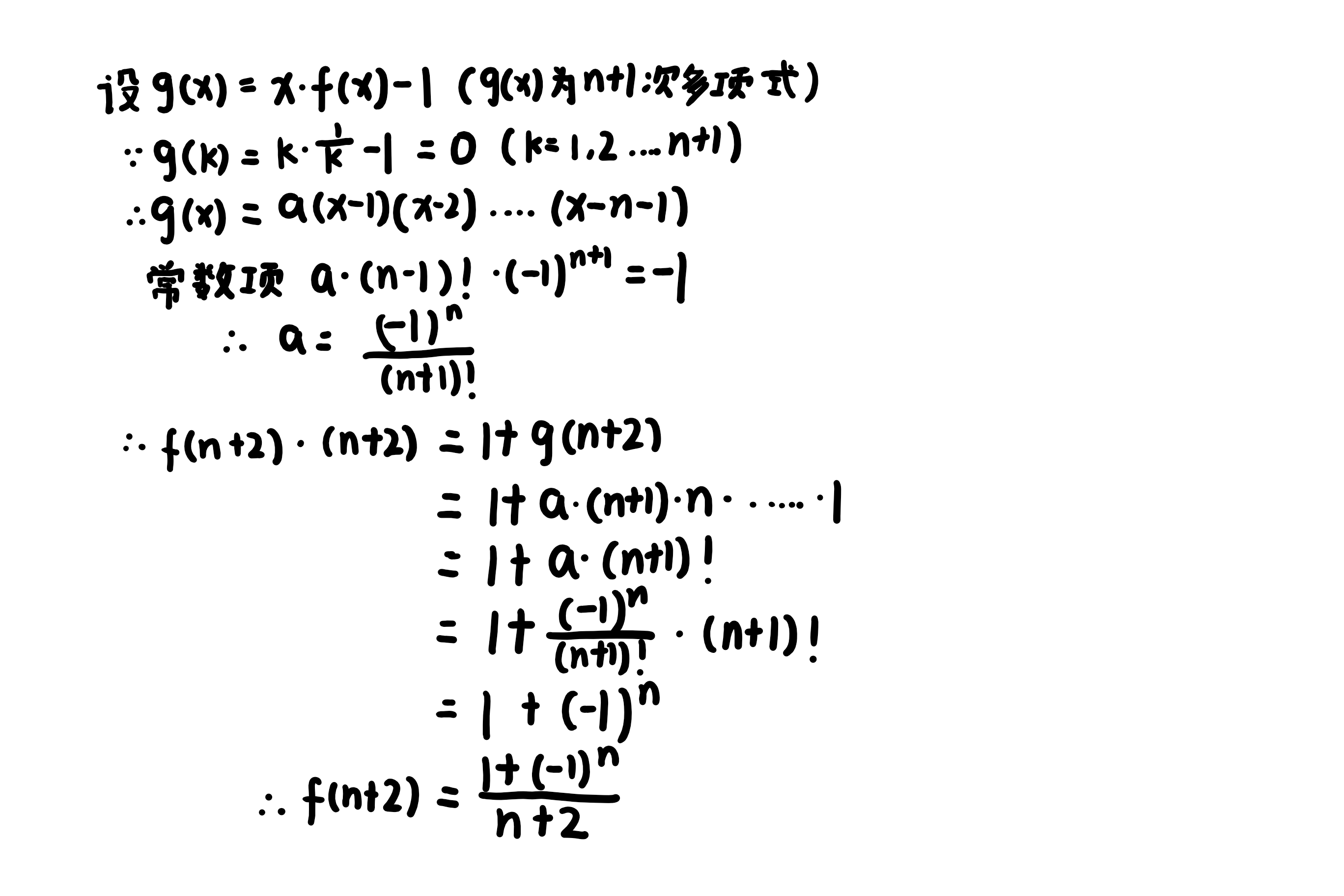
12.png

数列相关

常见的数列定理

二阶线性递推数列的特征方程

貌似一般比较经常用到的就是这个：

13.png

经典例题

Q3.1

14.png

求解过程如下：

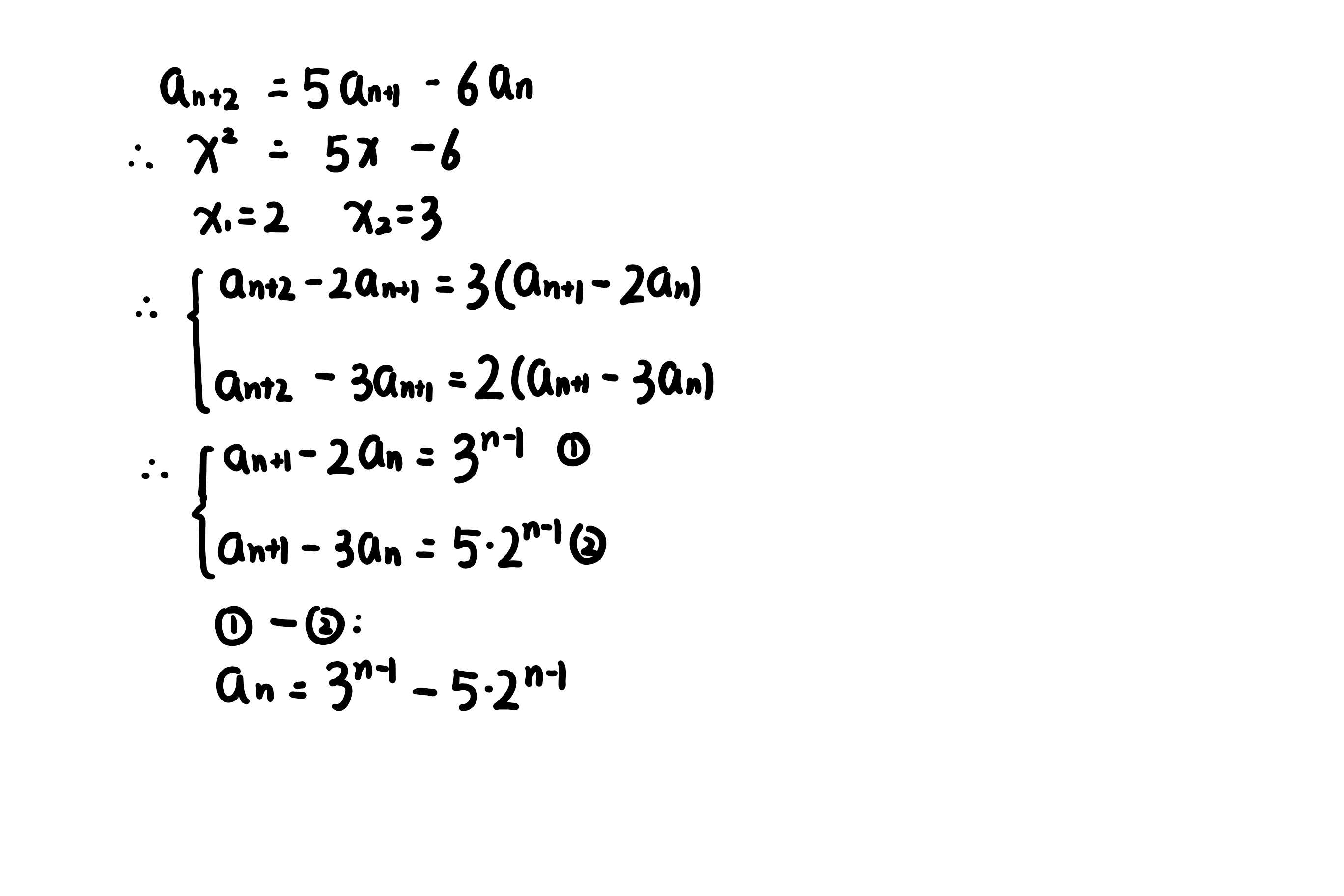
15.png

初等数论(划重点)

常见初等数论定理

（一）Bézout定理

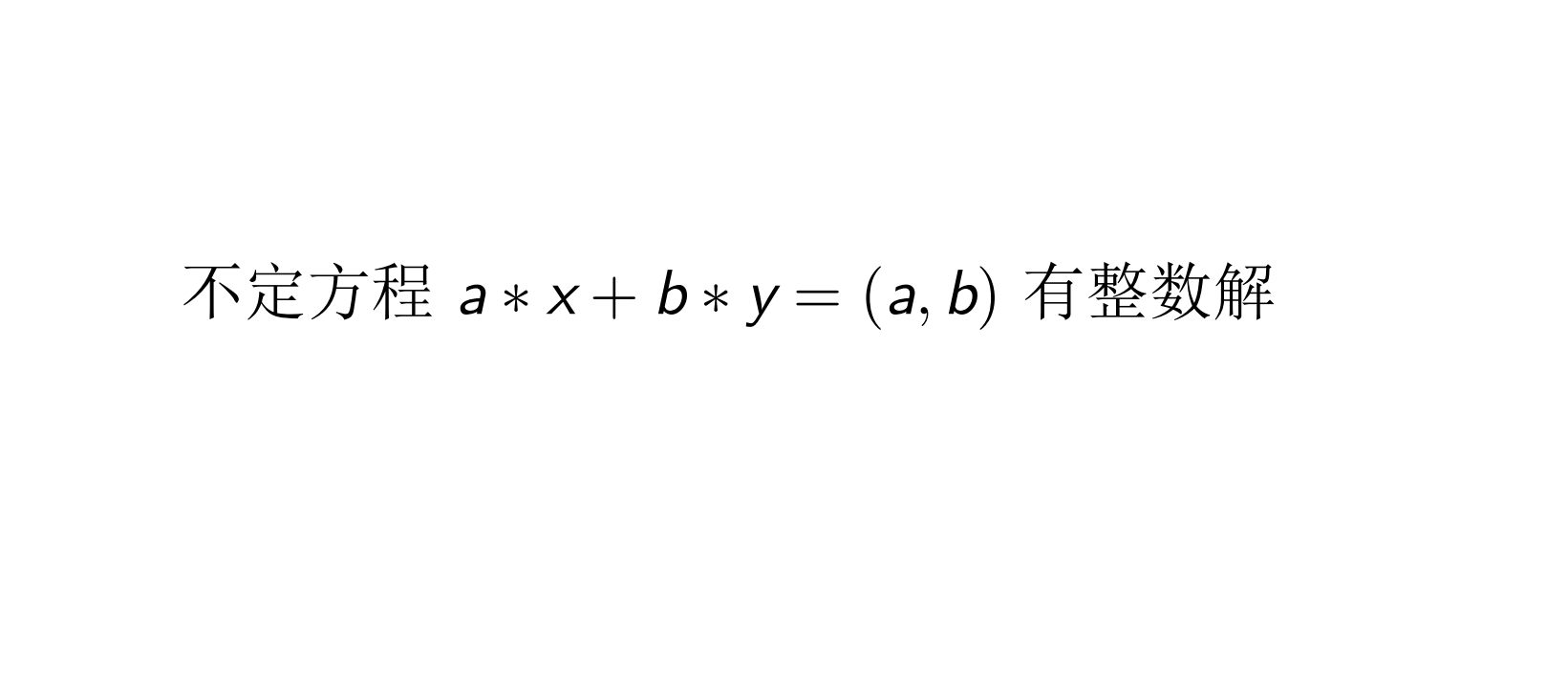
16.png

让我们从你们最熟悉的(数论只会的)gcd来理解一下：

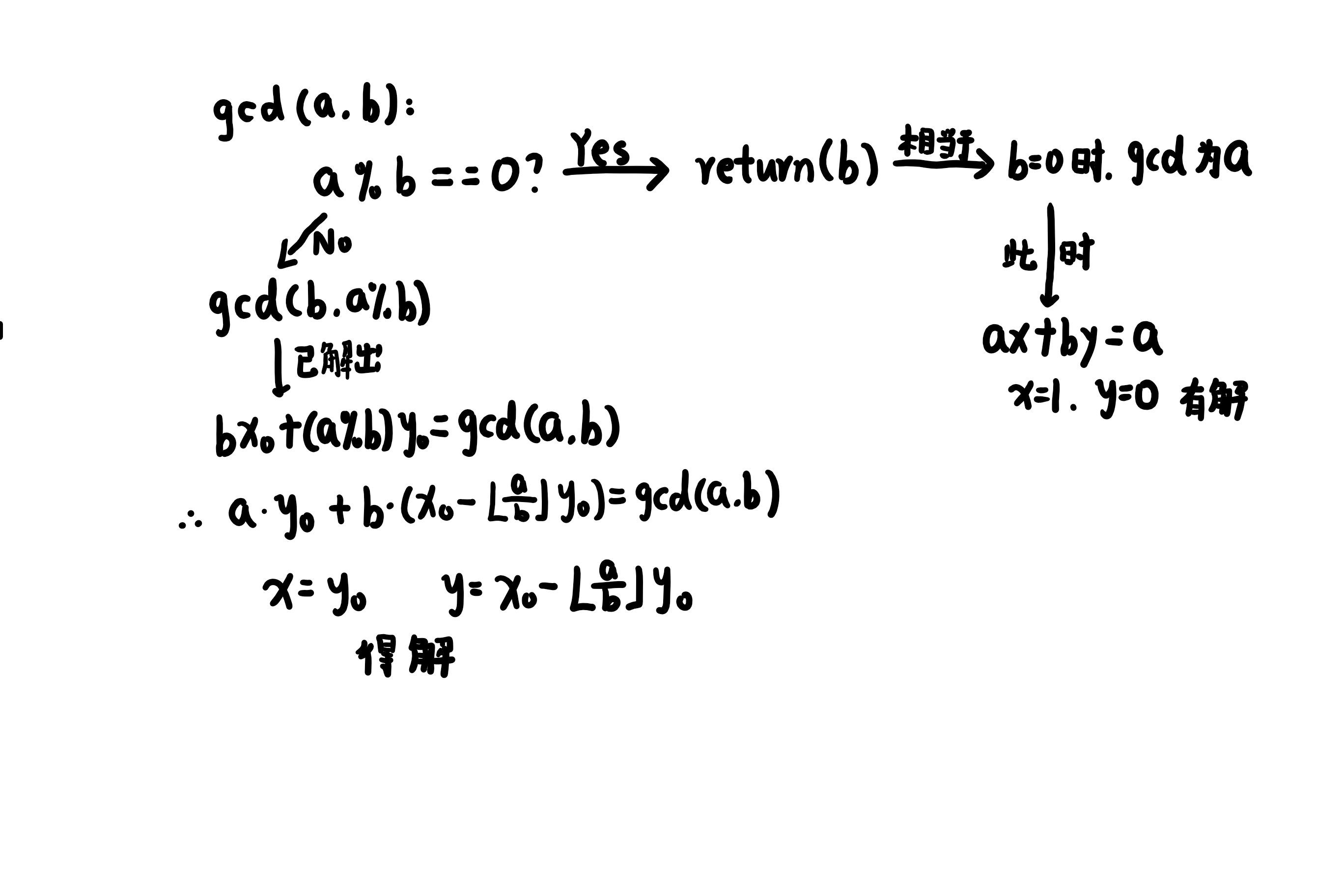
19.png

（二）Euler 定理

17.png

让我们来试着证明一下这个定理：

20.png

（三）中国剩余定理

18.png

其中 Mi^-1的意思是Mi在 % mi 意义下的逆元。

（四）Lucas 定理

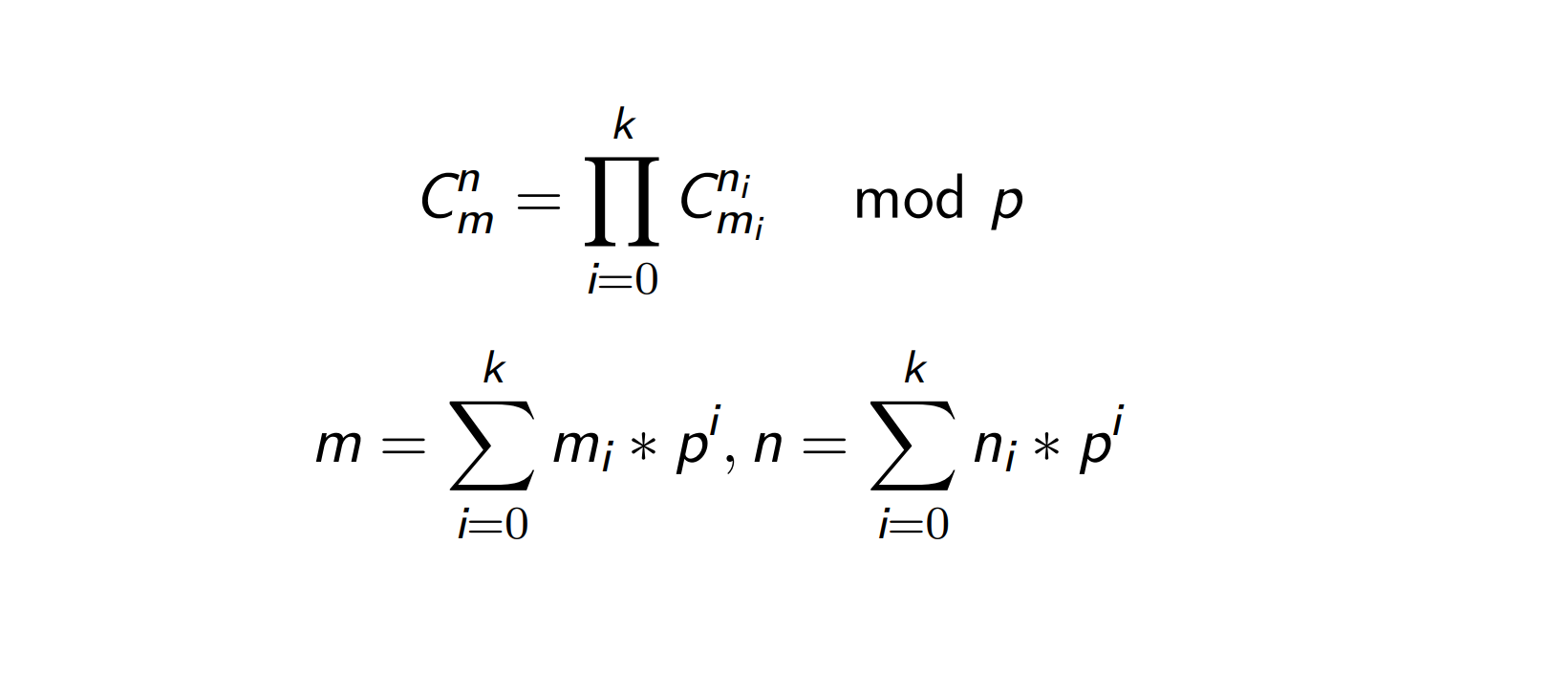
21.png

什么看不懂，没事下面我给出解释：

23.png

下面再给出证明：

24.png

（五）Dirichlet 定理

22.png

这个貌似在OI中很少用到，一般都运用在解析数论当中。

经典例题

Q4.1

25.png

过程如下：

31.png

Q4.2

26.png

证明如下：

32.png

Q4.3

27.png

过程如下：

33.png

Q4.4

28.png

过程如下：

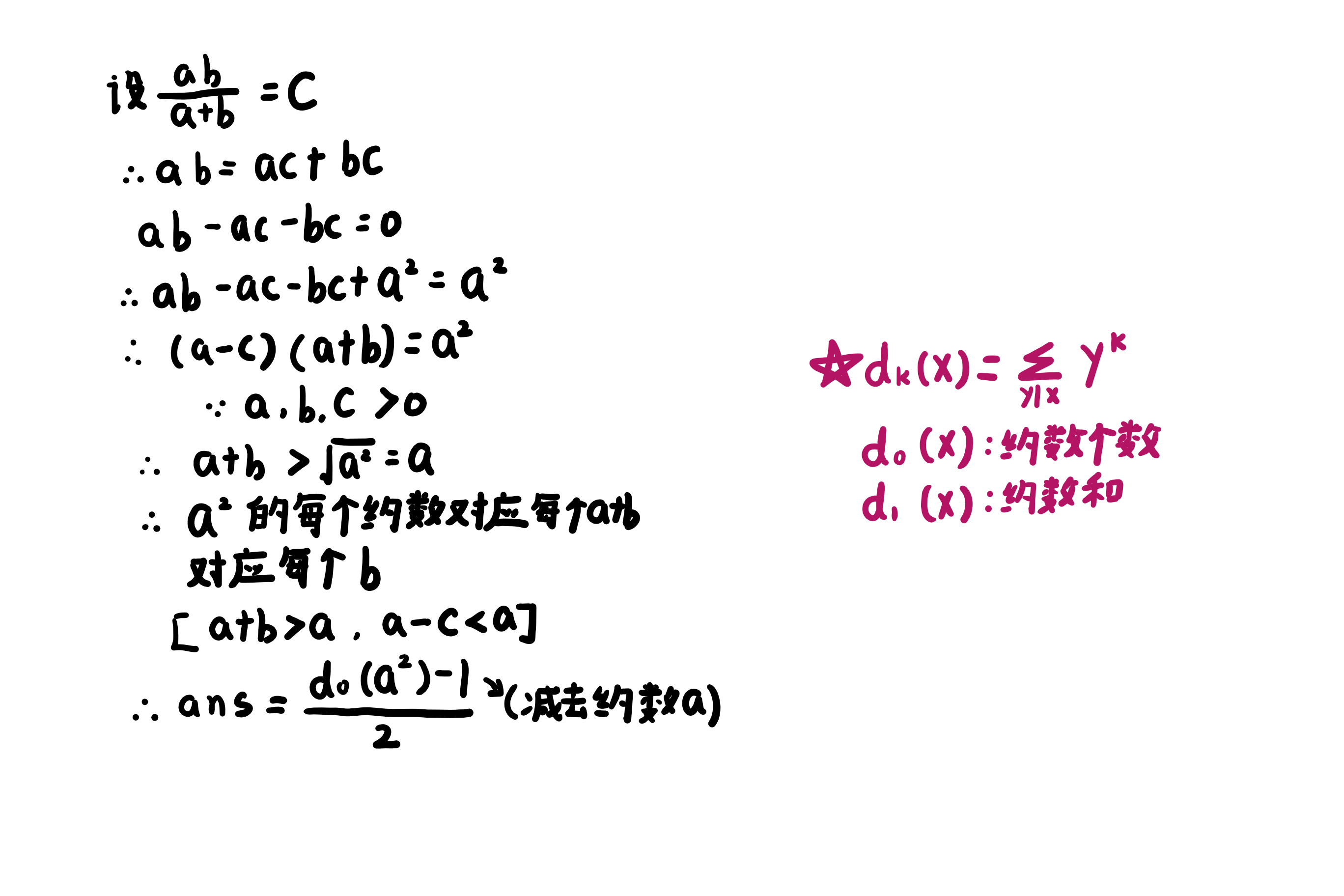
34.png

Q4.5

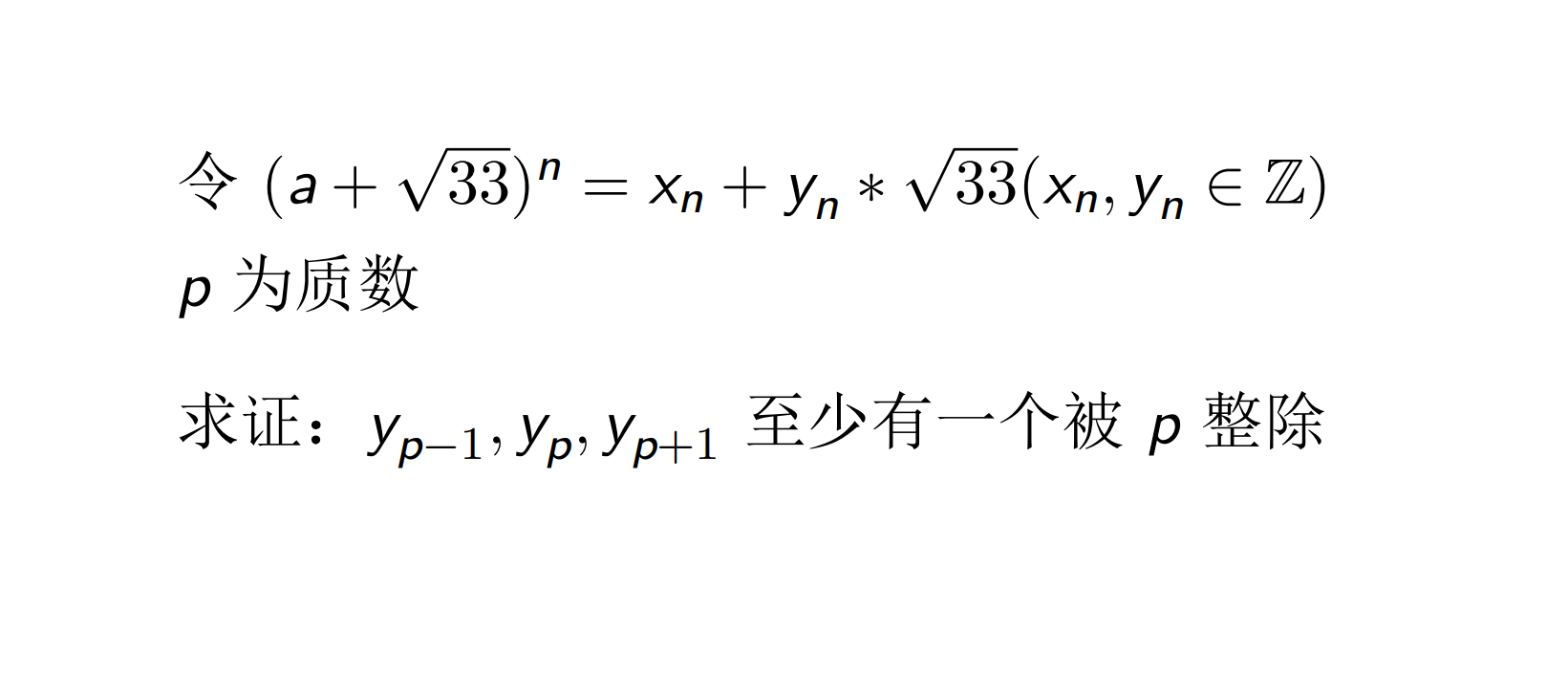
29.png

证明如下：

35.png

Q4.6

30.png

证明如下：

36.png

组合/图论

经典例题

Q5.1

37.png

解答过程如下：

40.png

Q5.2

38.png

证明过程如下：

41.png

Q5.3

39.png

证明过程如下：

42.png

结语

通过这节课，我们了解很很多有意思的MO题目，其中的题目有可能在未来的某一天就出现在OI的题面上，希望你有所领悟吧。最后希望你喜欢这篇BLOG！

Last modification：January 29th, 2019 at 10:06 pm
© 允许规范转载
If you think my article is useful to you, please feel free to appreciate