在信息学的诸多题目中，凡是求解单调函数或单峰函数，总是离不开二分和三分两种相似的算法，那么这篇BLOG，就让我们学习一下二分和三分算法吧！

应对单调函数的二分法

什么是二分法

二分法，顾名思义，就是把一个区间不断平分为两段的方法，其主要运用在求解单调函数上，比如下图，我们有个定义域在【l，r】上的单调递增函数f(x)，我要查询函数值为k的函数上的点的横坐标是多少，我们就可以查看一下f((l+r)/2)的函数值，如果f((l+r)/2)小于k，那么这个横坐标一定落在【l，(l+r)/2】之中；反之，如果f((l+r)/2)大于k，那么这个横坐标一定落在【(l+r)/2，r】之中，这就是比较广义的二分法。

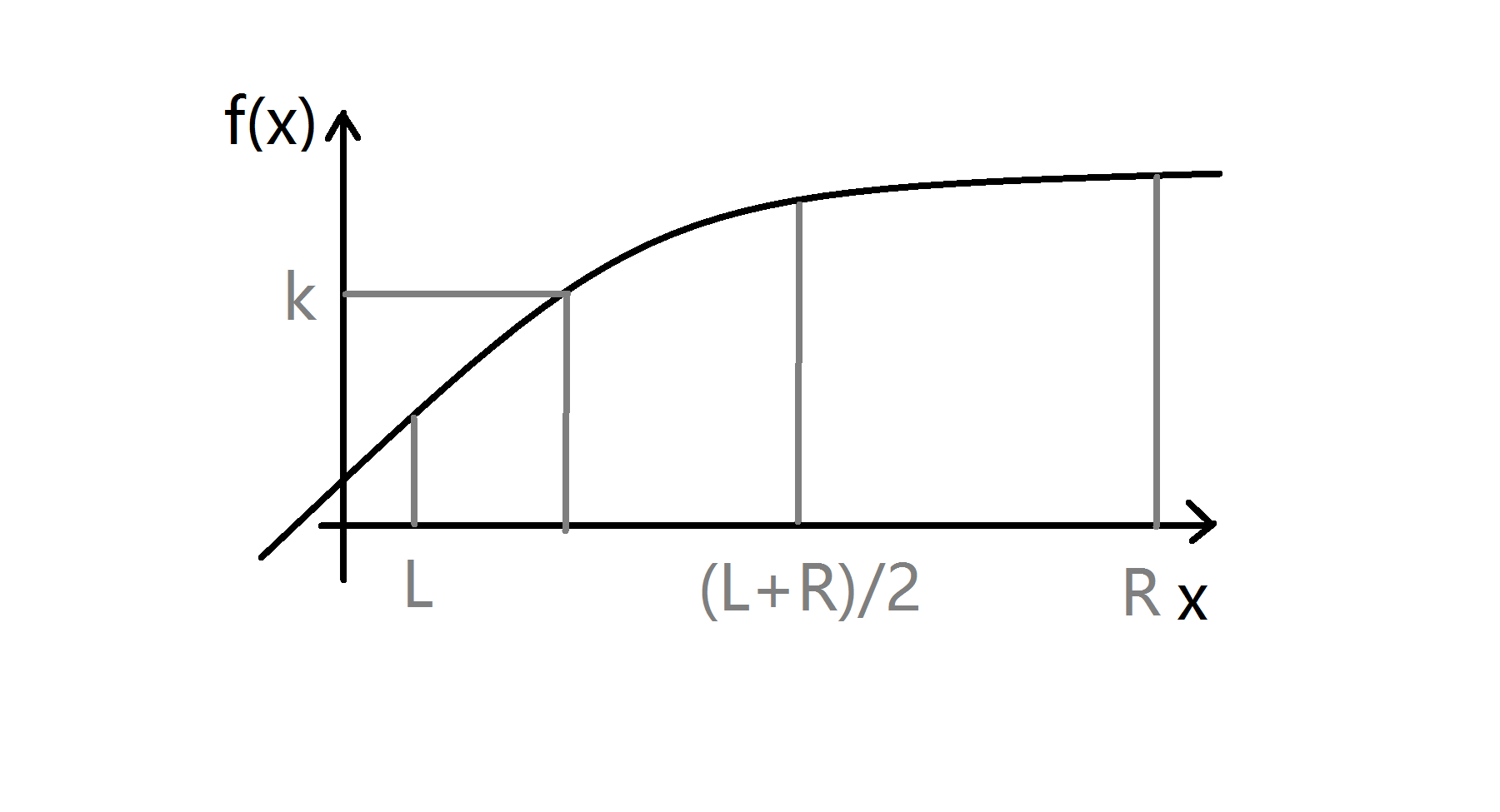
但是在实际的程序设计中，二分法更加广泛的应用于二分答案之中。比如我们要求解一个问题的答案，除了直接求解答案以外，如果我们可以证明答案是单调的（也就是说如果x可行，对于任意y≥x也可行 或者 如果x可行，对于任意y≤x也可行）的话，我们就可以用二分法在定义域中，找到一个最大或最小的，符合题目条件的答案，一般二分答案的题目，题目中总会有“最大值最小”或者“最小值最大的字眼”。下面就让我们从下面这些经典的例题当中体会一下吧！

经典例题

[tyvj p1359]收入计划

首先我们设领到工资最多的那一次工资数额为x，题目要我们求解的就是x的最小值，但是我们发现，貌似x不是很好直接求解，而且又出现了“最大值最小”的感觉，所以我们考虑能否二分答案x-min。

我们发现，最终答案x-min是单调的，怎么说呢？就是我们假如枚举x-min，x-min=1时可能不满足条件，x-min=2时可能不满足条件，x-min=3时可能不满足条件…………突然，x-min=100时满足条件了！那么x-min=101，x-min=102，x-min=103………………都能满足条件！所以说x-min是存在单调性的！

但是直接枚举x-min的话显然是会超时的，所以我们二分一下x-min，以下界l=0，上界r=全部工资总和，来二分寻找一个最小的满足条件的x-min。每次二分到一个mid=(l+r)/2，我们就check一下，用O(n)的时间复杂度去判断一下我们二分到的这个mid可不可行；若可行，则在【l，mid】中继续二分，若不可行，则在【mid，r】中二分即可。

至于如何判断，我们只要贪心的想就好了。我们想，如果取m次工资，每次取得工资的最大值一定大于等于取m+1次工资，每次取得工资的最大值。所以我们只要计算出每次取得工资都要小于等于mid的取钱次数x就行了。如果x小于等于m，那么就是可行的，反之就是不可行的。所以我们只要从第一天开始，刚开始得到的钱为0，往后循环。对于每一天我们都判断一下，如果当前得到的钱数加上今天要得到的钱数大于我们的mid，那么就把得到的钱之前得到的钱取出来，然后将这一轮得到的钱就设为今天得到的钱，代表今天把前段时间的工资取了出来，从今天开始一轮新的工资积累。反之如果当前得到的钱数加上今天要得到的工资小于等于我们的mid，那就欣然存下工资，就直接继续下一天就好啦，这样就完成了对答案的判断。

[51nod p1105]第K大的数

首先，我们发现，要直接求解第k大的数，是很麻烦的，因为我们要把所有的数算出来，而n的范围，已经不允许我们这么做了。所以我们考虑二分答案。

我们二分一个最终的答案m，显然我们现在的问题就是，如何判断m是合法的？其实很简单，我们记c数组中小于等于m的数有dm个，我们只要找到让dm==k的最小m就行了，所以问题转化为了如何快速求解dm？

很显然，我们先把a和b数组分别从小到大排好序，假如排好序后的序列为：

a1 a2 a3 ………… an
b1 b2 b3 ………… bn

我们发现，由于b[j]是单调递增的，所以我们对于每个a[i]，只要找到最后一个b[j]，使得a[i]b[j]≤m即可了。我们又发现，由于a[i]是递增的，所以随着i的递增，ai在递增，a[i]b[j]≤m最后个满足条件的bj要越来越小。所以我们发现随着i的递增最后一个满足条件的b[j]的j是递减的！所以我们只要暴力枚举出a[1]对应的b[j1]，然后对于a[2]对应的b[j2]一定小于等于b[j1]，a[3]对应的b[j3]又一定小于等于b[j2]……所以我们只要维护一个指针指向a[i]对应的b[j]就行了；然后在处理a[i+1]时，只要判断当前指针指向的b[j]可不可行（即能否满足a[i+1]*b[j]≤m），如果不可行，指针就一直前移直到可行，求出的便是a[i+1]对应的b[j]。

到这里这道题就做完了！

[JROJ]分数规划

这题初看貌似什么思路都没有，我们先设我们最后得出的最大值为x，很显然，如果x可行，对于任意y≤x，y都可行，所以x满足二分性质，接下来我们考虑如何二分。

由于x是我们的最大值，也就是说x是∑ai/∑bi≥x 的最大值，所以我们设∑ai/∑bi≥x。我们先两边同乘∑bi，再移项得到 ∑ai-x∑bi≥0。接下来就很简单了，我们只要先二分答案，二分出x，然后把每一项按照 ai-xbi 排序，选取最大的m个数加起来判断是否大于等于零就可以了。如果大于等于零则该x可行，反之则不可行。

[JROJ]最大比例生成数

这题和上一题分数规划类似，我们先设我们最后得出的最大值为x，一样的，如果x可行，对于任意y≤x，y都可行，所以x满足二分性质，接下来我们考虑如何二分。

和上一题一样由于x是我们的最大值，也就是说x是∑ai/∑bi≥x 的最大值，所以我们设∑ai/∑bi≥x。我们先两边同乘∑bi，再移项得到 ∑ai-x∑bi≥0。接下来就很简单了，我们只要先二分答案，二分出x，然后把每一边的边权设定为 ai-xbi ，然后跑最大生成树。如果最大生成树的边权之和大于等于零则该x可行，反之则不可行。

[luogu U33406]纽约

这道题很容易想错，一看到题目，很容易觉得是直接二分答案，然后你就WA了。为什么呢？

因为二分要满足的性质是若w可行那么如果w'≥w，那么w'一定也可行，但是在这道题中，由于塞物体顺序条件的限制，你画一些例子就可以发现，当w可行时w+1不一定可行。那这是不是代表着我们无法二分了呢？不是的，我们在分析一下就能发现，如果w可行，那么w+max{wi}一定可行！[感性的理解一下，如果w可行，w+max{wi}相当于原方案中每一辆车能再塞一件最大的物体，那肯定是可行的啊！

所以我们先二分答案找出一个w使得w可行，w-1不可行，然后暴力判断一下区间[w-max{wi},w],找出满足条件的最小值即可。

到这里，二分的主要模型都讲解完了。

应对单峰函数的三分法

什么是三分法

这个内容在之前的暴力算法讲解中也讲过，这里再讲一遍吧。

首先，什么是单峰函数？顾名思义就是只有一个峰的函数，即其导数值等于0的点有且只有一个。如下图，左图和中图都是单峰函数，但是右图就不是单峰函数：

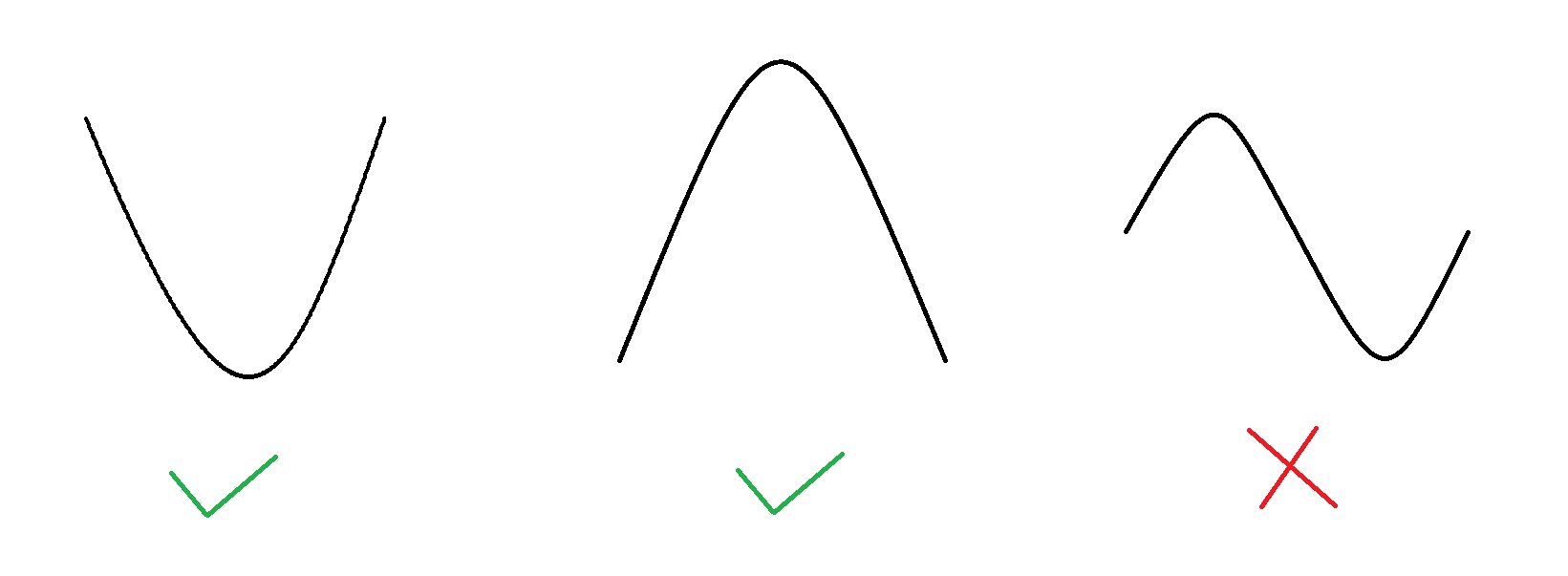
那么什么是三分呢？我们都知道，在单调函数f(x)中[x包含于[l,r]]，寻找某个给定数我们一般用二分；但是在单峰函数中，我们若是要寻找极值点，一般都是使用三分去寻找，我们以有极小值的单峰函数为例子，我们首先将函数图像三等分，得到中间的两个三等分点a，b，此时两者的函数值f(a),f(b)分为三种情况：

（1) f(a)小于f(b)
这时分为两种情况，a，b在极值点两侧和极值点同一侧，如下图：

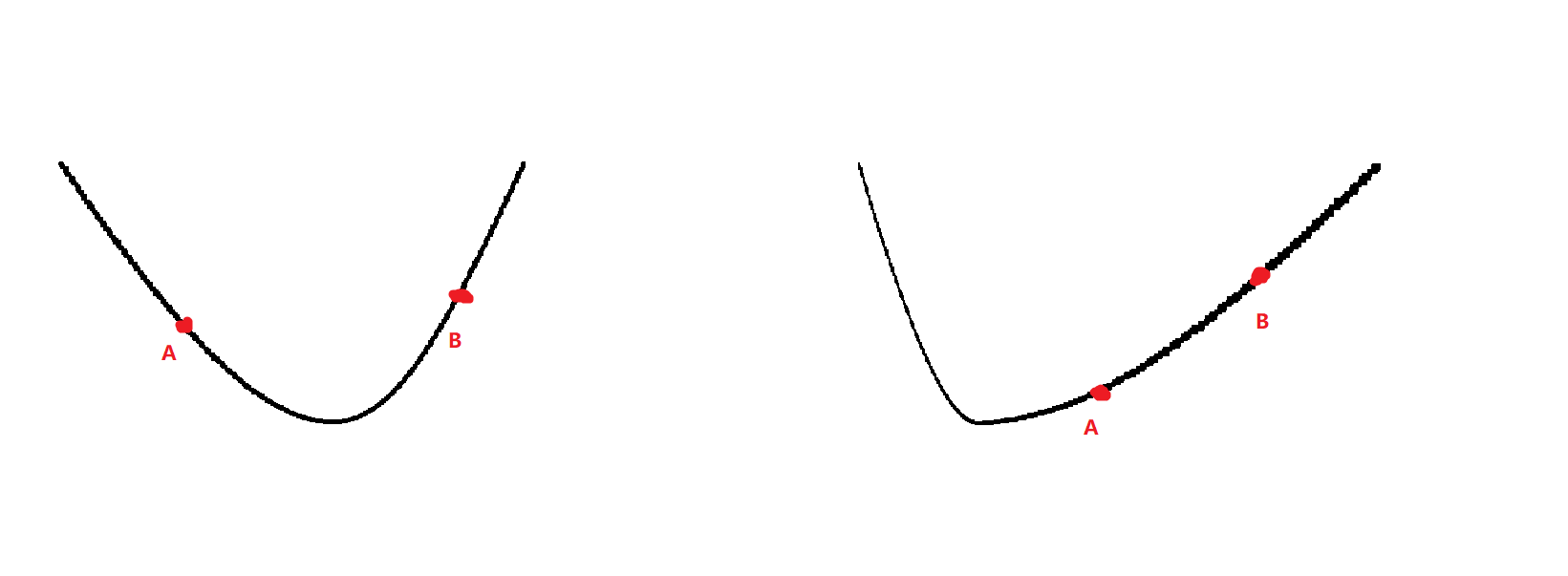
但是我们可以发现，极值点一定出现在左端点l到三分点b上，所以我们可以缩小三分范围到【l，b】。

（2) f(a)等于f(b)

这个没什么好说的，a，b不重合，那么a，b一定在极值点两侧，所以极值点范围一定可以缩小到【a，b】。

（3) f(a)大于f(b)

这时同样分为两种情况，a，b在极值点两侧和极值点同一侧，如下图：

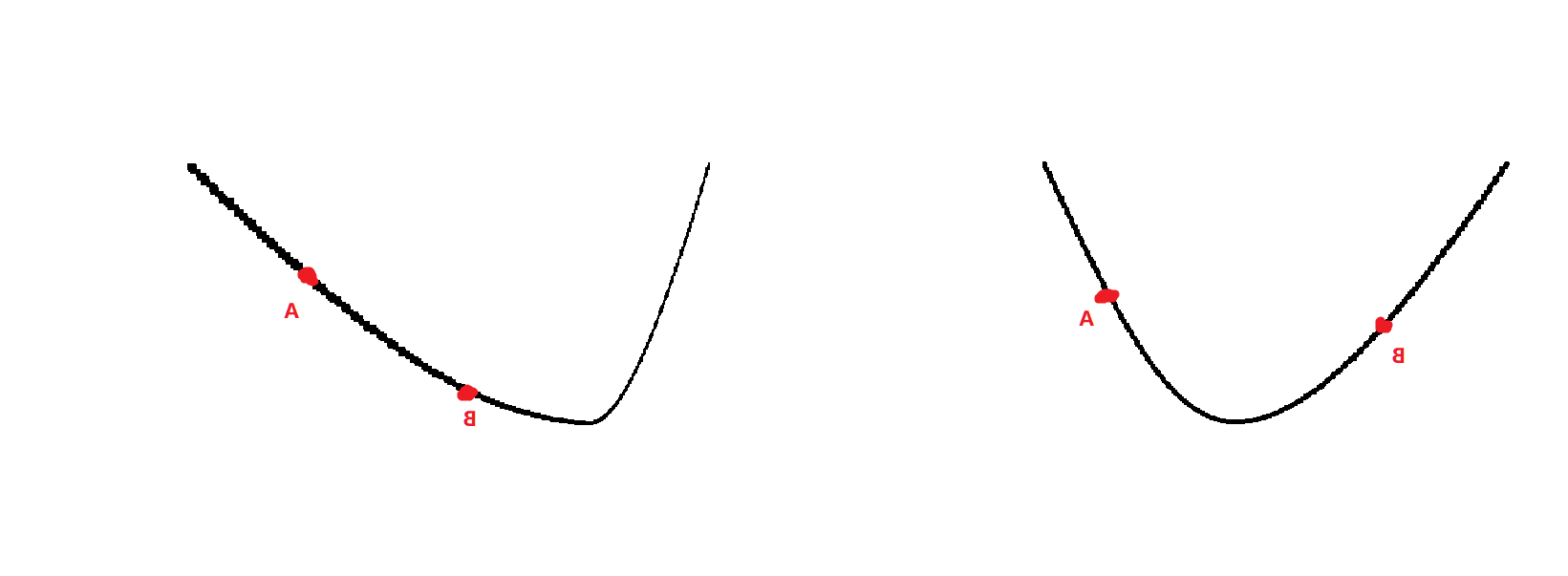
但是我们可以发现，极值点一定出现在三分点a到右端点r上，所以我们可以缩小三分范围到【a，r】。

所以三分大致程序如下：

double l=0,r=1e9;

for(int i=1;i<=100;i++)//100可以改大，越大精度越高 
{
    double a=l+(l+r)/3;
    double b=r-(l+r)/3;
    if(f(a)>f(b))  l=a;
    else if(f(a)<f(b))  r=b;
    else{l=a;r=b;} 
} 

经典例题

[NKW]E-迎风舞

首先我们根据常识知道，斜抛的水平距离与与抛射角θ成凸函数关系[即θ从0到Π/2，水平距离先增加后减少]，所以就是一个三分的裸题了，接着我们推导一下水平距离与θ的关系，得到水平距离x关于θ有：

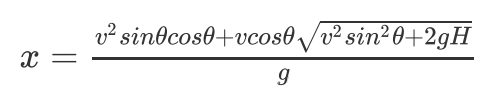
所以直接三分就能得到θ了！

结语

那么二分和三分的技巧和模型就讲到这里啦！这类题目重要的是能看出要用二分或三分解决并且证明这样做是对的，这需要做题经验的积累。那么最后，希望你喜欢这篇BLOG！