提到NOIP高分的秘诀，不少人脱口而出的就是“暴力”。但是纯纯的暴力，也就是朴实无华的搜索肯定是无法通过大部分NOIP题目的（签到题当我没说），今天我们就从十道例题一起来学习一下搜索的艺术（为了提升学习效果，请阅读这篇BLOG的同学在阅读每道题思路之前自觉独立思考十分钟左右）。

题一 扑克牌

题目描述:

给你 n 张扑克牌，保证这 n 张来自于同一副（也就是说相同数字的牌不会超过四张）。你可以打若干次牌，第一次可以打任意数字，之后每次打的数字，必须是之前打过的数字之和的约数。问是否存在一种打牌方案，使得可以打出所有牌，输出方案。1 ≤n≤ 52。

解题思路:

首先，一个显而易见的做法是直接搜索，搜索过程中记录前面的数字之和，枚举还没有选的牌，只选可能的牌作为下一张。 然而很明显，这样的数据量，这么做是通过不了的。

我们考虑一下优化。搜索是一定的，我们的瓶颈出现在哪里？对！就是搜索的状态太多了，那么如何减少状态数呢？

没错，我们可以尝试倒着搜索！搜索过程中记录剩下的牌的数字之和，只选可能的牌作为前一张。显然状态数会少很多。 这样可以通过了。

可能有同学会问了，这样倒着搜为什么状态数就减少了呢？我们知道一般的深搜，随着层数的增加，情况是成指数级增长的，所以前面层数的状态少了能优化整体状态的数量。我们看下面两幅图，左边描述的是正着搜索，第一步有大量的走法；而右边这幅图则描述的是倒着搜索，很显然，第一步比前者就已经少了大量的走法了。很明显，前面的搜索决策的减少势必能减少整体的搜索量。

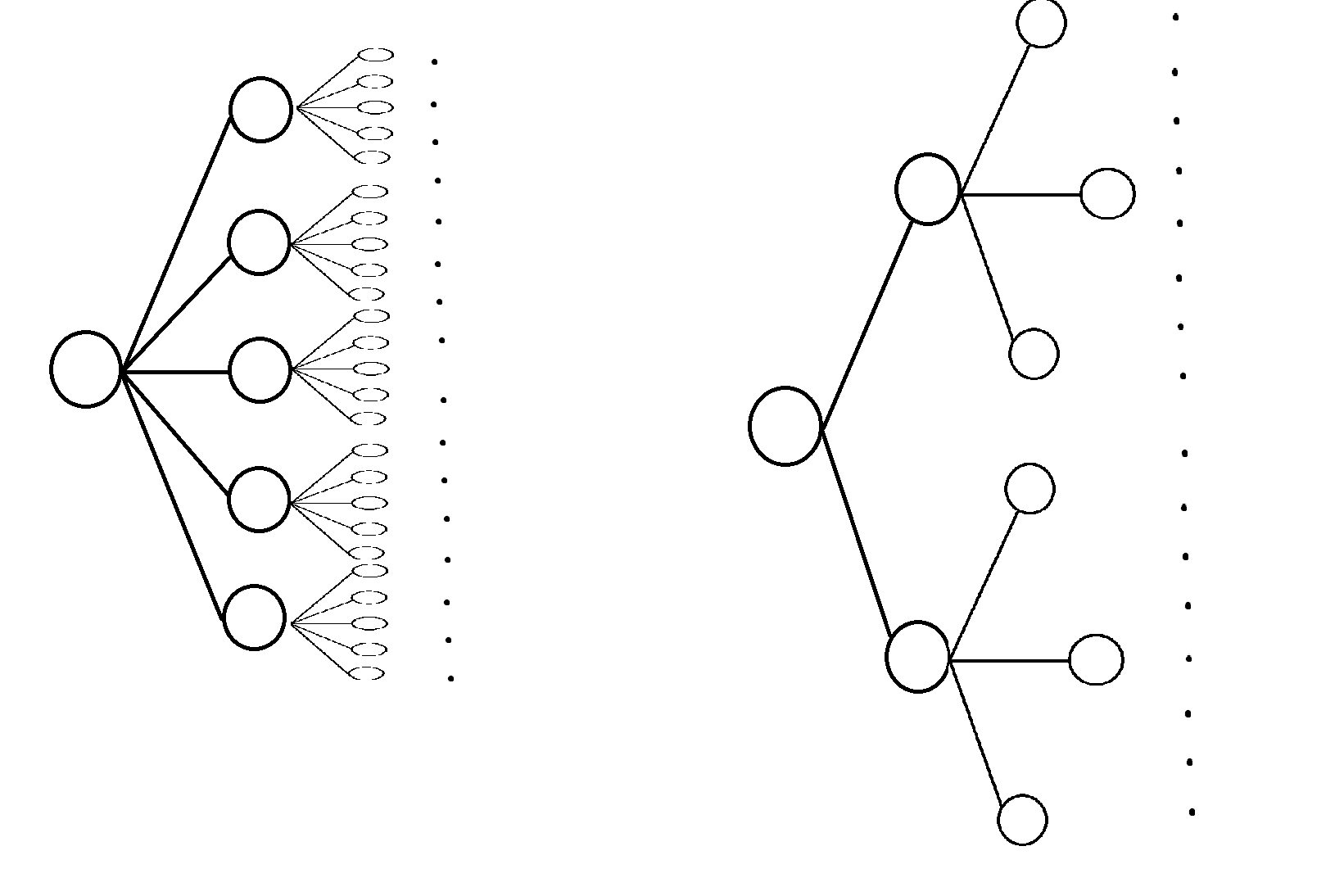
这样我们就能通过这道题了。

题二 价值最大子序列

题目描述:

给出一个由’a’, ’b’, ’c’ 组成的长度为 n 的字符串。 定义一个子序列 T 的价值为 (lenT)^2/cT ，其中 lenT 表示 T 的长 度，cT 表示 T 的最小循环节长度。 找出价值最大的子序列。 1 ≤n≤ 10^4。

解题思路:

首先，我们还是可以写出一个朴素的搜索算法，先枚举循环节，找满足条件的子序列，最后输出答案。还是非常好写的，但是很显然的是，这样做是会超时的。

我们换一种思路，由于这是一个只由’a’, ’b’, ’c’ 组成的长度为 n 的字符串，所以我们由抽屉原理可以知道，’a’, ’b’, ’c’当中肯定有一种字符的数量是大于等于n/3的。

那么知道这个有什么用呢？我们假如只把只含’a’, ’b’, ’c’当中数量最多的字符的子序列提取出来当作答案，那么长度 lenT≥n/3 ，cT=1 ，所以此时我们得到的答案为 n^2/9，也就是说，最终的答案一定大于等于n^2/9。

又因为我们最后得到的子序列长度一定小于等于n，所以我们可以得出最优情况下，子序列的最小循环节长度不会超过8，这时我们自需要暴力枚举所有长度不超过 8 的字符串，作为最小循环节，更新答案即可。

题三 最短欧几里得距离

题目描述:

给出平面上 n 个点 (xi,yi)，要求找到平面上的一个点 (x,y)【也就是说最后的最优答案点不一定在n个点当中】，使得这 个点到给出的那些点的欧几里得距离之和最短，要求保留四位小数。 1 ≤n≤ 1000。 −10^6 ≤xi,yi ≤ 10^6。

解题思路:

由于我们得到的答案点可能是平面上的任意一个点，而且答案还不是整点而是坐标带小数点的点，这时我们的正常的暴力就无从下手了。

我们感性的认识一下，假设当 x 固定时，当我们选的点的y很大时，答案很大；y很小时，答案也很大；当y在中间时，可以取得一个最小值；所以我们猜测答案随着 y 的变化是一个单峰函数。所以对 于一个给定的 x，可以通过三分法求出最优的 y。

这时我们再假设，对于每一个x，我们都求出了其x固定时最优的y。同样的，对于每个x已经找到了对应的最优的y，当x很大时，答案很大；x很小时，答案也很大；当x在中间时，可以取得一个最小值；所以我们又能猜测最优答案随 x 的变化也是一个单峰函数，所以可以通过三分套三分求出最优的 x，同时得到最优的 y。【至于严谨的证明需要用到微积分的知识，我毕竟是个蒟蒻当然不会啦，感兴趣的同学可以自己证明一下】

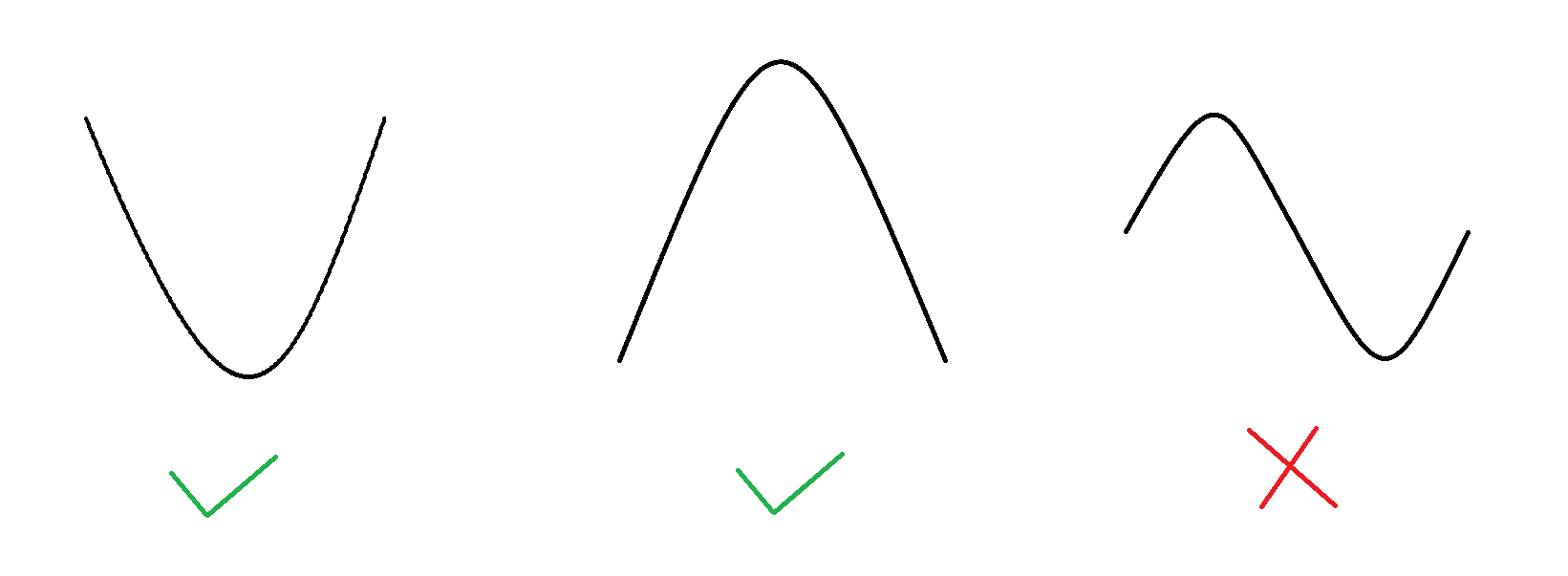
什么你不知道什么是单峰函数，什么是三分，没事我慢慢讲给你听。首先，什么是单峰函数？顾名思义就是只有一个峰的函数，即其导数值等于0的点有且只有一个。如下图，左图和中图都是单峰函数，但是右图就不是单峰函数：

那么什么是三分呢？我们都知道，在单调函数f(x)中[x包含于[l,r]]，寻找某个给定数我们一般用二分；但是在单峰函数中，我们若是要寻找极值点，一般都是使用三分去寻找，我们以有极小值的单峰函数为例子，我们首先将函数图像三等分，得到中间的两个三等分点a，b，此时两者的函数值f(a),f(b)分为三种情况：

（1) f(a)小于f(b)
这时分为两种情况，a，b在极值点两侧和极值点同一侧，如下图：

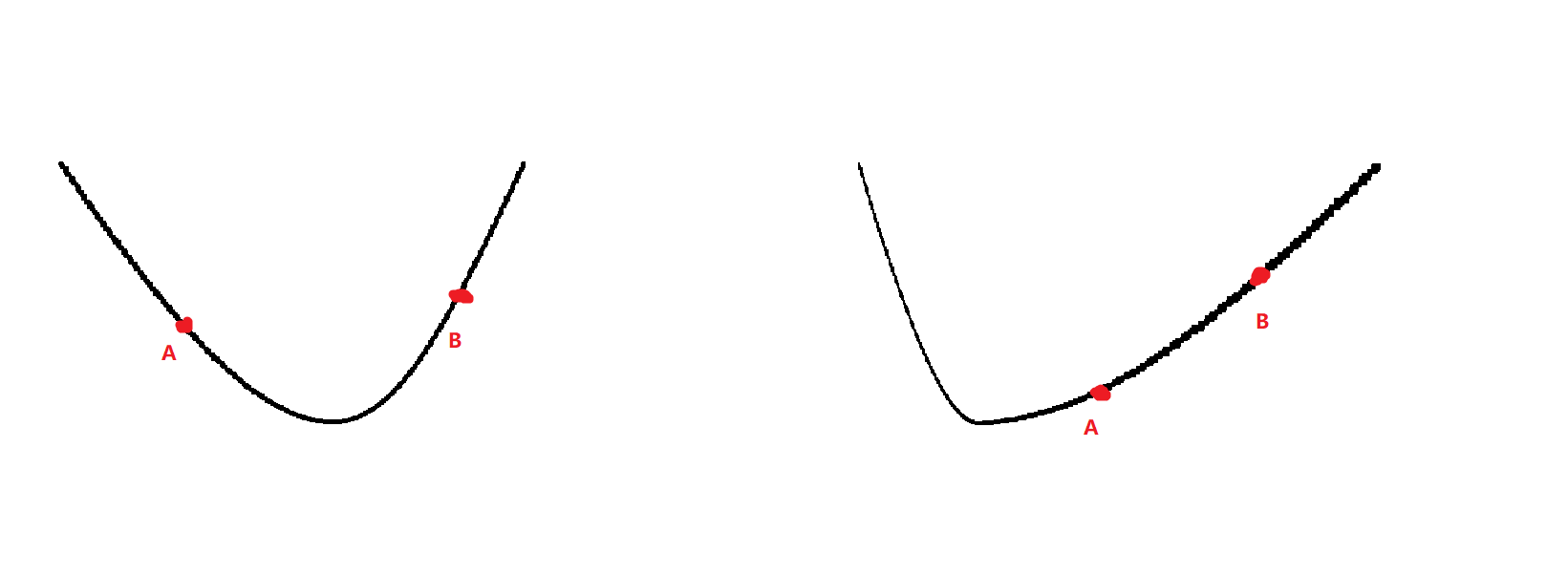
但是我们可以发现，极值点一定出现在左端点l到三分点b上，所以我们可以缩小三分范围到【l，b】。

（2) f(a)等于f(b)

这个没什么好说的，a，b不重合，那么a，b一定在极值点两侧，所以极值点范围一定可以缩小到【a，b】。

（3) f(a)大于f(b)

这时同样分为两种情况，a，b在极值点两侧和极值点同一侧，如下图：

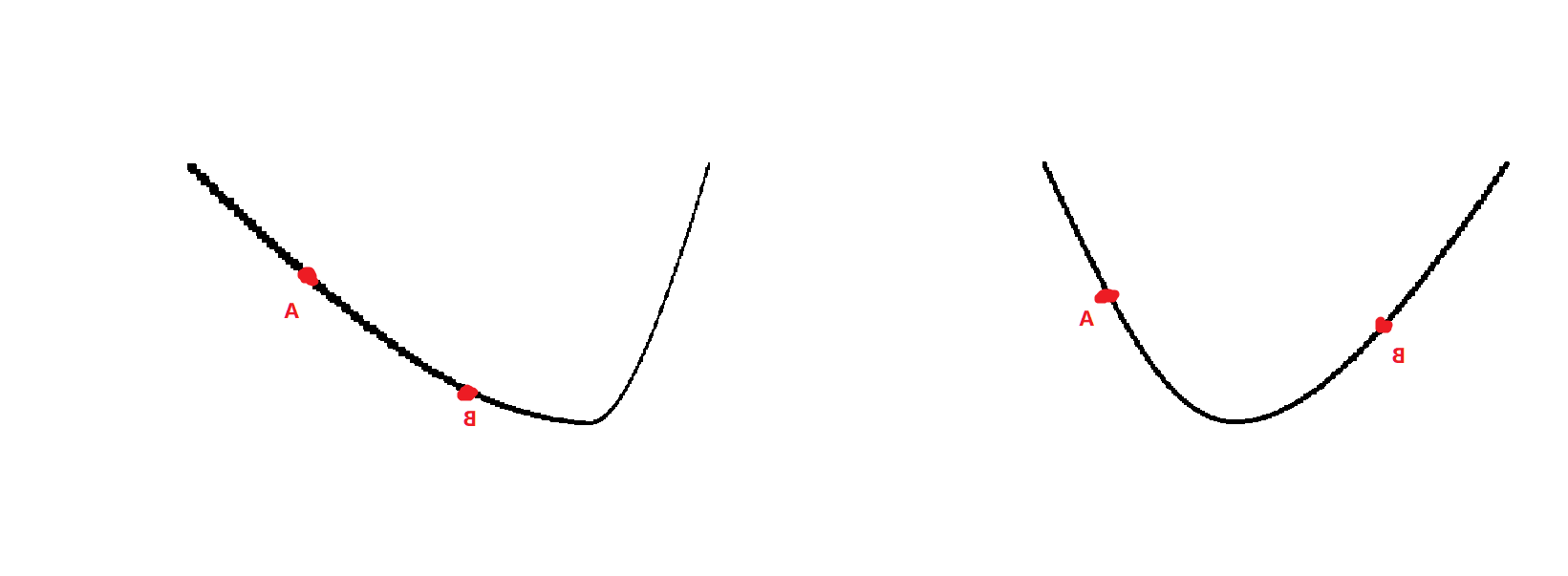
但是我们可以发现，极值点一定出现在三分点a到右端点r上，所以我们可以缩小三分范围到【a，r】。

三分大致程序如下：

double l=0,r=1e9;

for(int i=1;i<=100;i++)//100可以改大，越大精度越高 
{
    double a=l+(l+r)/3;
    double b=r-(l+r)/3;
    if(f(a)>f(b))  l=a;
    else if(f(a)<f(b))  r=b;
    else{l=a;r=b;} 
} 

题四 新定义运算

题目描述:

定义 ′ 运算如下：
如果 p = 1，p′ = 0。
如果 p 是质数，p′ = 1
否则 p′ = (a×b)′ = a′ ×b+a×b′
给出 k,r，求出所有满足 x′ = kx,1 ≤x≤r 的 x。 1 ≤k≤ 30,1 ≤r≤ 2×10^18。

解题思路:

很明显传统的暴力会超时。我们先观察一下：当P为两个质数的乘积时，即 p=p1*p2（p1，p2均为质数），我们有p'=p1'*p2+p1*p2'=p1+p2;同理，当P为三个质数的乘积时，即 p=p1*p2*p3（p1，p2，p3均为质数），我们有p'=p1'*p2*p3+p1*p2'*p3+p1*p2*p3'=p1*p2+p2*p3+p1*p3;

通过观察我们不难得到若p=p1*p2*p3*……*pk,那么我们有p'=∑(p1*p2*p3*……*pk)/pi。简化一下：

因为 pi 为质数，所以不可能出现这种情况：qx/px 和 qy/py 都不 是整数，而他们的和为整数。也就是说 qi/ pi 必须为整数。 即对于一个 pi，其在 n 中的次数必定为 pi 的倍数。所以把 形如 p^p 的数拿出来，暴力搜索从中选 k 个可以组成的数[可以重复旋转]，方案数即为答案。

题五 糖水

题目描述:

给出 n 杯糖水，第 i 杯糖水的总质量为 mi，其中糖的质量 为 ti。现在给出一个分数 a/b，问能否选出若干杯糖水，使得这些杯混合之后，糖的质量占总质量之比为 a/b。 2 ≤n≤ 35。 1 ≤ti ≤mi ≤ 10000。 1 ≤a≤b≤ 10000。

解题思路:

这道题又有一个很明显的做法，暴力的枚举每杯糖水取或者不取，然后判断最终浓度是否等于a/b，很显然，超时是一定的，那么如何操作呢？

这里要教会大家一个新技巧——折半搜索！顾名思义，就是把搜索内容先折半再合并的神奇搜索方法。

题六 玩具

题目描述:

Johnny 有若干个玩具，玩具的种类可能相同也可能不同。 现在已知他的这些玩具有 n 个本质不同的子集（包括空集），问 玩具的个数可能是多少。输出所有的可能解。 1 ≤n≤ 109。

解题思路:

假设 Johnny 有 ai 个玩具 i，那么显然会有∏(ai + 1)个本质不同的子集。所以换句话说，题目也就是要求：如果 n = a1a2...ak，∑ai 有哪几种可能？

所以我们只要暴力分解n的因数就好了。由于 ai 的顺序不影响答案，所以不妨让 ai 以非降序分布。假如如果现在要决策 ak，且 ∏ai = t （i包含于[1,k-1]）；那么 ak 一定是 n/t 的约数，且ai 以非降序分布，ak一定大于等于上一个数，所以我们只要根号分解约数即可

题七 立方体最短路径

题目描述:

给定一个 a×b×c 的长方体，定义其表面上两个点的距离 为沿着长方体表面走的最短路径的长度。找到距离最远的点对的 距离，且其中一个点为长方体的顶点。 1 ≤a,b,c≤ 1000。

解题思路:

这时就有同学会认为，体对角线就是最长的呀！没错，在正方体当中这时正确的，但是在长方体当中，这时一个错误的结论那我们应该这么做呢。

我们先选一个角为起始点（红点），很明显，另一个点会落在三种颜色分别标记的三个面上：

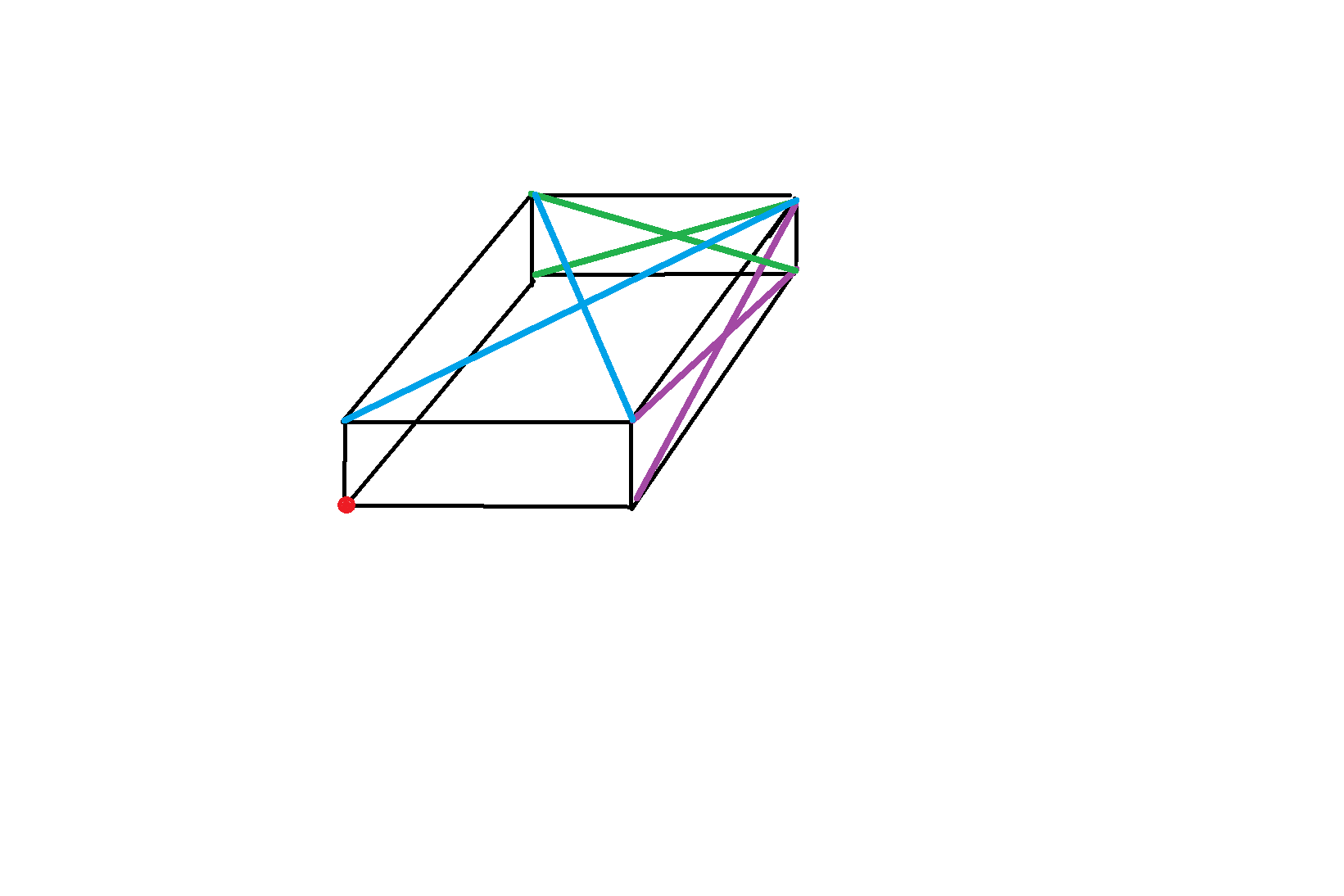
然后在处理这三个面的时候都是一样的，所以我们以上底面为例子，我们先以红点建立空间直角坐标系：

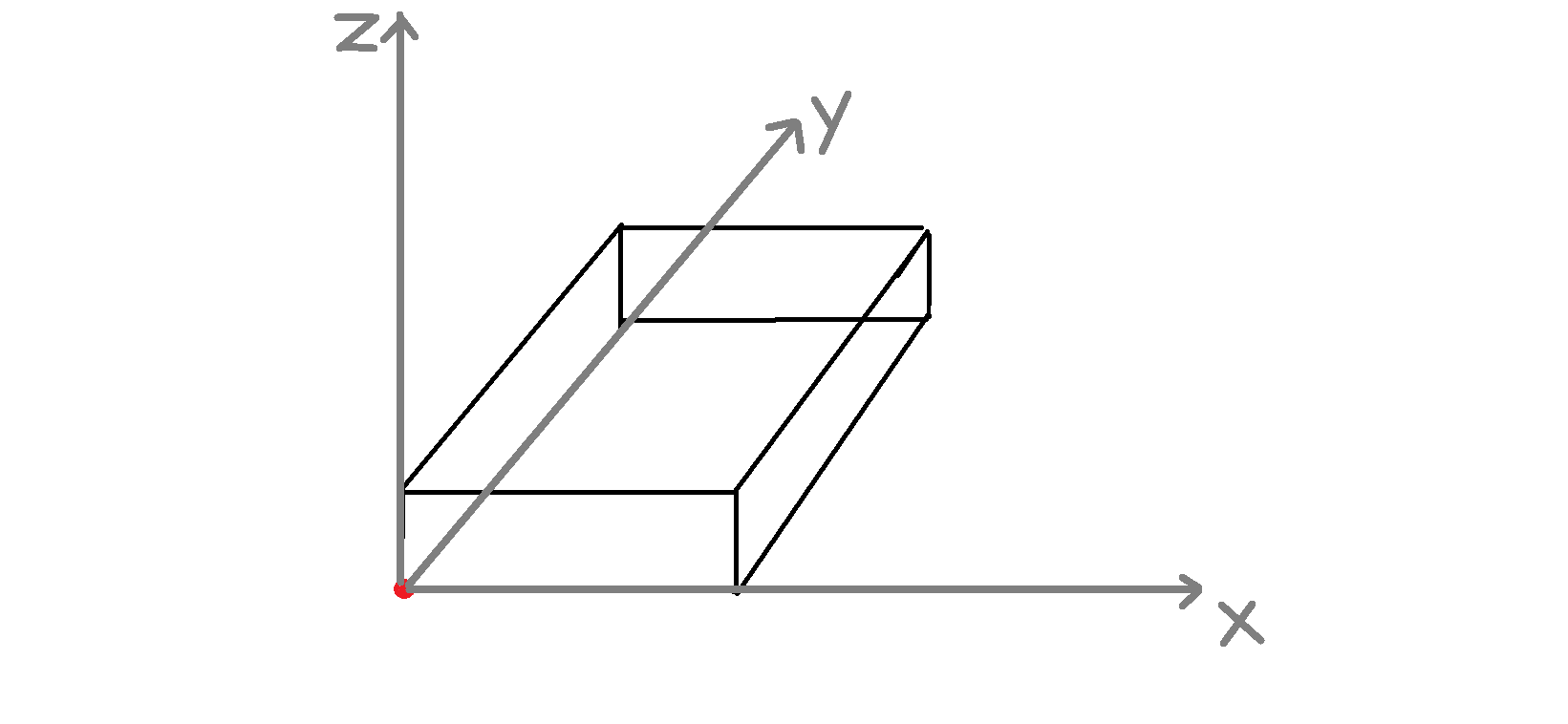
这时我们的目标点就落在了z=c的面上，也就是说这时我们要在z=c上找到一个点，使得它到我们起始点的最短距离最大。

这时我们发现，当 x 固定时，最远距离是关于 y 的一个单峰函数，可以三 分求解。

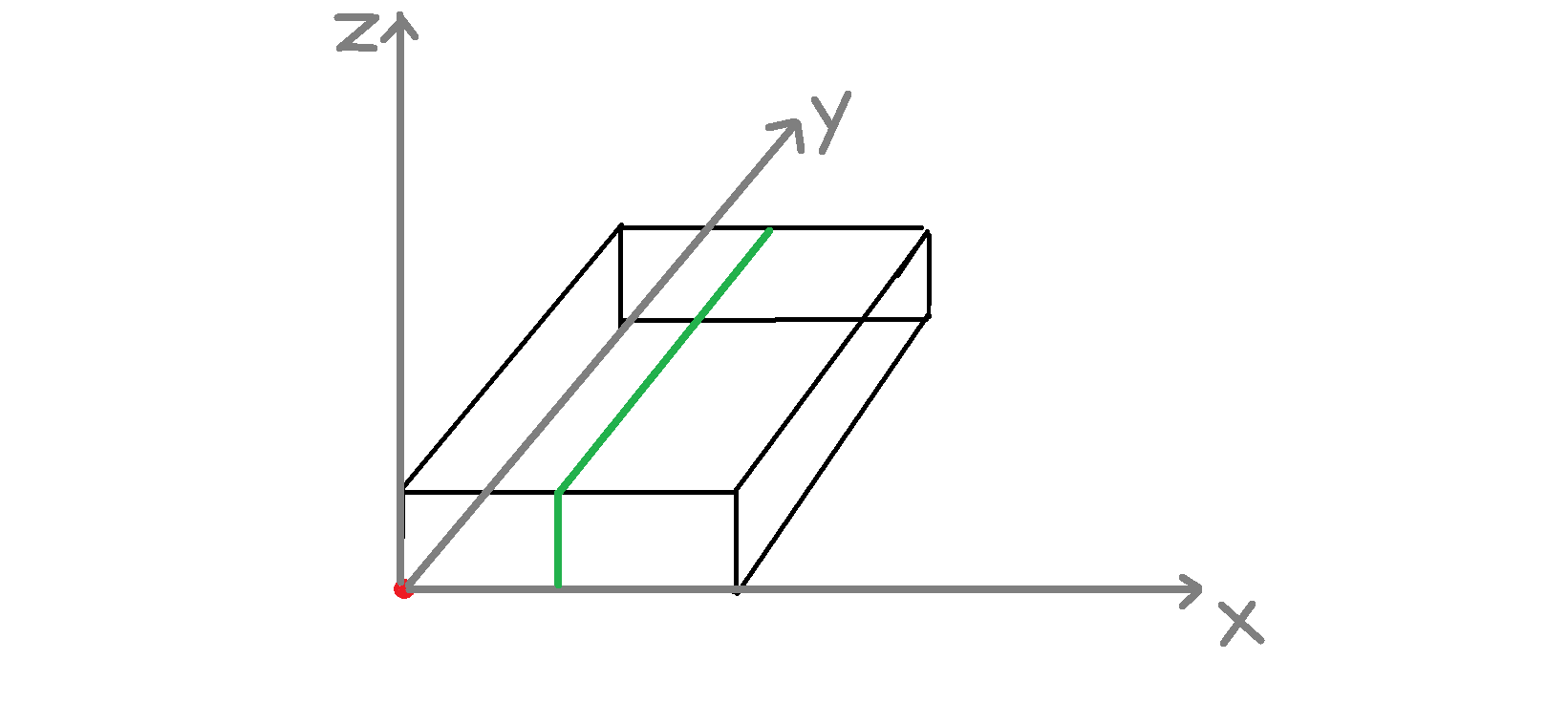
对于不同的 x，最优答案随 x 的变化也是一个单峰函数，所 以可以通过三分套三分求出最优的 x，同时得到最优的 y。

所以又是运用熟悉的三分套三分，我们解决了这道题。

题八 随机图求最短路

题目描述:

给出一个 n 个点 m 条边的随机生成的无权无向图，有 q 次 询问，每次给出 x,y(1 ≤x,y≤n,x̸= y)，询问 x 到 y 的最短路。 n = 10^5,m = 3×10^5,q = 10^4。

解题思路:

又由一个很显然的做法，floyed，但是超时也是不可避免的，那么这道题的突破点在哪里呢？

图是随机的！由于图是随机生成的，两点间的最短路期望大约是 6。对于 一次询问，分别从起点和终点开始 BFS 四层，即双向广搜通过共同访问过的点更新答案。如果没有共同访问过的点，那么就暴力求两点间 的最短路，由于这种情况的概率很小，所以不会影响复杂度。所以总的复杂度还是很优秀的。

题九 进贡

题目描述:

给出一个 n 个点 m 条边的无向图连通简单图。每条边的长 度为 1；第 i 个点种有 vi 个金币。 小偷住在 1 号点，王宫在 2 号点，小偷需要沿着到王宫的 最短路去进贡。在去进贡的途中，对于经过的每个点，他都可以 选择偷或不偷。如果偷，他将获得这个点的金币，但是回程时将 不能访问这个点。 小偷想知道在他能回家的前提下，最多可以进贡多少金币。 2 ≤n≤ 36,1 ≤m≤ n(n−1)/2。

解题思路:

这道题的思路还是很妙的。想到了做法的话还是非常简单的。首先我们要知道，对于一个简单无向图来说，两点间的最短路的条数约为O(e^(n/e)) 级别。

所以可以搜索出所有的最短路出来逐个判断。 回程时不能经过偷过金币的点的限制可以如下转换：去程在所有点都偷窃，回程如果经过去程经过的点，那么扣除这个点的金币。显然这样与原来是等价的。

所以对于每一条最短路，先算出这条路径上的金币之和，再算一下从王宫到小偷家的最小费用，相减更新答案即可。

即正向路程最短路+反向代价最短路即可完成。

题十

题目描述:

给出 n 个数 a1,a2,··· ,an，相邻两数间的空隙可以填 + 或 −，问有多少种填法，使得运算结果等于 x。 2 ≤n≤ 35。 −1000 ≤ai,x≤ 1000。

解题思路:

看到 2 ≤n≤ 35 ，就在暗示我们这是一道折半搜索的题目了！我们把n个数分为【1，n/2】和【n/2+1，n】两组，分别求出运算结果的值，但是要注意，当我们分界点n/2和n/2+1中间的符号为-时，后面的符号要全部改变而不能直接减去后半部分的值。比如 1-2+3！=1-(2+3)。需要特别把握一下。

结语

到这里，我们常见的十种暴力模型就讲完了，希望你能有所收获。最后希望你喜欢这篇BLOG！