超级久没有码BLOG了，超级想念当时搭BLOG的感觉……可是现在我已经是一株高三的苍老蒟蒻了，所以更新速度会慢很多，望谅解。下面就让我们一起走进国庆的第一场模拟赛吧！

A 最长距离

问题描述：
windy有一块矩形土地，被分为 NM 块 11 的小格子。 有的格子含有障碍物。 如果从格子A可以走到格子B，那么两个格子的距离就为两个格子中心的欧几里德距离。
如果从格子A不可以走到格子B，就没有距离。 如果格子X和格子Y有公共边，并且X和Y均不含有障碍物，就可以从X走到Y。
如果windy可以移走T块障碍物，求所有格子间的最大距离。 保证移走T块障碍物以后，至少有一个格子不含有障碍物。
输入格式
输入第一行包含三个整数，N M T。 接下来有N行，每行一个长度为M的字符串，’0’表示空格子，’1’表示该格子含有障碍物。
【数据规模】
20%的数据，满足 1≤N,M≤30 ； 0≤T≤0 。
40%的数据，满足 1≤N,M≤30 ； 0≤T≤2 。
100%的数据，满足 1≤N,M≤30 ； 0≤T≤30 。
输出格式
输出包含一个浮点数，保留6位小数。
样例输入
【样例输入1】
3 3 0
001
001
110
【样例输入2】
4 3 0
001
001
011
000
【样例输入3】
3 3 1
001
001
001
样例输出
【样例输出1】
1.414214
【样例输出2】
3.605551
【样例输出3】
2.828427

这题比赛的时候搞了我快两个小时……还是没看出这题表面上叫做最长距离，实际上是一道最短路的题目QwQ什么你也没看出，没关系，我来慢慢告诉你。

我们观察发现，题目最开始给我们的是一个网格图，有的格子是1，表示有障碍物，有的格子是0，表示没有障碍物，就像下面这幅图一样：

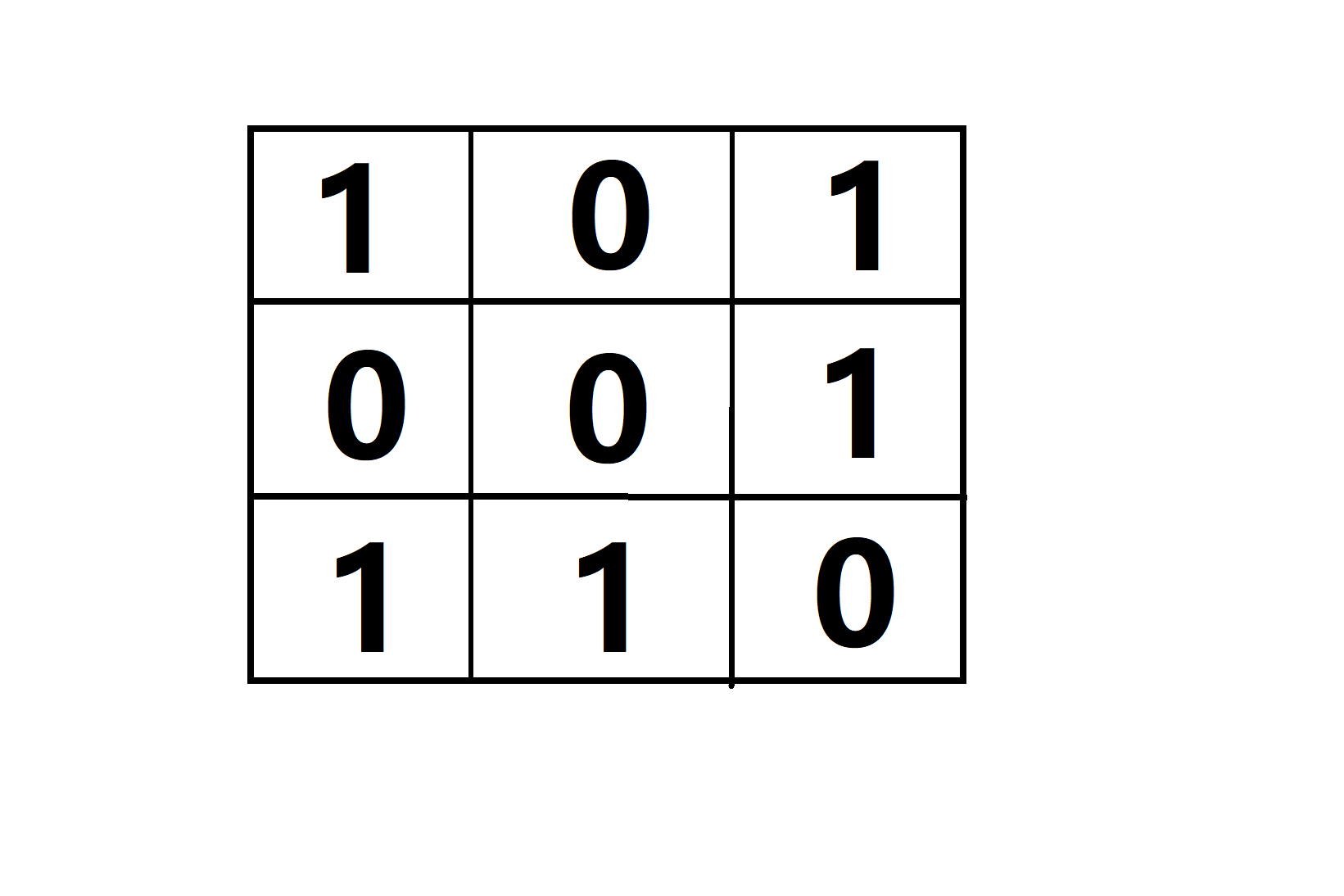
现在我们就可以让个相邻节点建边了。由于规定走到的节点一定要为0，所以我们让任意一条边，如果走到节点值为0的点，那么边权就为0；如果走到节点值为1的点，那么边权就为1，就像下面这幅图一样：

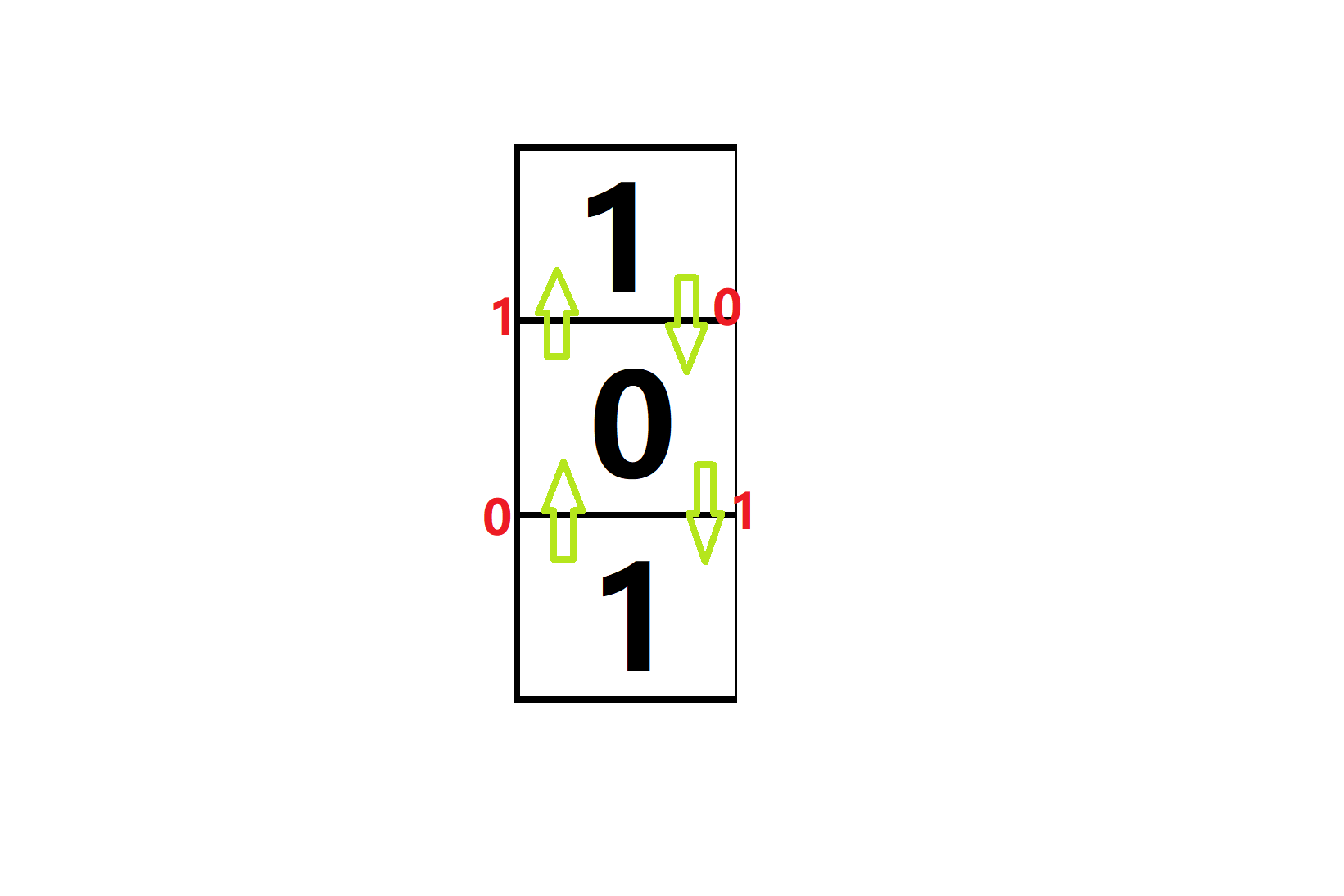
OK，那我们再把某一点值为0的点，设为起点，从该点出发跑单源最短路径，跑出来的结果是什么？没错!就是这个点到达任一点的最小代价！那思路就很显然了！我们枚举起点，然后跑SFPA，找到所有与他在代价小于等于T的条件下联通的点，求出其中最大的欧几里德距离就是我们要的答案了！总的复杂度为O((NM)^2)。

特别需要注意的是，可能会出现刚开始给你的图一个为0的格子都没有，这个时候就要特判一下下，让最左上角也就是（1，1）的点变为0，然后T--，相当于先开辟一个点。

下面附上代码：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
struct node
{
    int x,y,num,next;
}f[11000];
int a[1100][1100],last[11000],g[11000],vis[11000];
int list[1100000],head,tail;
char s[1100];
int i,j,k,m,n,o,p,jl,num,t,x,y;
double js,ma;
int ins(int u,int v,int k)
{
    num++;
    f[num].x=u;f[num].y=v;f[num].num=k;
    f[num].next=last[u];last[u]=num;
    return 0;
}
int main()
{
    scanf("%d%d%d",&n,&m,&t);
    for(int i=1;i<=n;i++)
    {
        scanf("%s",s+1);
        for(int j=1;j<=n;j++)
        {
            a[i][j]=s[j]-'0';
            if(a[i][j]==0)jl++;
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(i>1)ins((i-1)*m+j,(i-2)*m+j,a[i-1][j]);
            if(j>1)ins((i-1)*m+j,(i-1)*m+j-1,a[i][j-1]);

            if(i+1<=n)ins((i-1)*m+j,i*m+j,a[i+1][j]);
            if(j+1<=m)ins((i-1)*m+j,(i-1)*m+j+1,a[i][j+1]);
        }
    }
    if(jl==0)
    {
        a[1][1]=0;
        t--;
    }
    ma=0;
    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
    {
        if(a[i][j]==0)
        {
            memset(g,63,sizeof(g));
            memset(vis,0,sizeof(vis));
            g[(i-1)*m+j]=0;head=1;tail=2;
            list[head]=(i-1)*m+j;vis[list[head]]=1;

            while(head<tail)
            {
                x=list[head];
                for(int k=last[x];k;k=f[k].next)
                {
                    y=f[k].y;
                    if(g[x]+f[k].num<g[y])
                    {
                        g[y]=g[x]+f[k].num;
                        if(vis[y]==0)
                        {
                            vis[y]=1;
                            list[++tail]=y;
                        }
                    }
                }
                vis[x]=0;
                head++;
            }

            for(int ii=1;ii<=n;ii++)
            for(int jj=1;jj<=m;jj++)
            {
                o=(ii-1)*m+jj;
                if(g[o]<=t)
                {
                    js=sqrt((i-ii)*(i-ii)+(j-jj)*(j-jj));
                    if(js>ma)ma=js;
                }
            }
        }

    }
    printf("%0.6lf",ma);
    return 0; 
} 

B 扑克牌

问题描述：
你有n种牌，第i种牌的数目为ci。另外有一种特殊的牌：joker，它的数目是m。
你可以用每种牌各一张来组成一套牌，也可以用一张joker和除了某一种牌以外的其他牌各一张组成1套牌。
比如，当n=3时，一共有4种合法的套牌：{1,2,3}, {J,2,3}, {1,J,3}, {1,2,J}。
给出n, m和ci，你的任务是组成尽量多的套牌。每张牌最多只能用在一副套牌里（可以有牌不使用）。
输入格式
第一行包含两个整数n, m，即牌的种数和joker的个数。第二行包含n个整数ci，即每种牌的张数。
【样例解释】
输入数据表明：一共有1个1，2个2，3个3，4个joker。最多可以组成三副套牌：{1,J,3}, {J,2,3}, {J,2,3}，joker还剩一个，其余牌全部用完。
【数据规模】
50%的数据满足：2 < = n < = 5, 0 < = m < = 10^ 6, 0< = ci < = 200。
100%的数据满足：2 < = n < = 50, 0 < = m, ci < = 500,000,000。
输出格式
输出仅一个整数，即最多组成的套牌数目。
样例输入
3 4
1 2 3
样例输出
3

这是一道比较有意思的题目，下面提供两种思路的解法，分别是从正面和从侧面的做法：

解法一：从正面进行操作：
我们观察一下题目，我们发现这道题其实可以用贪心去做。通过观察我们可以知道每一套牌中，JOKER不是必须的，所以我们会想，能不能把JOKER当成普通牌来看待呢？

当然可以，我们对问题进行一下变形，把JOKER当做一张普通牌来看待，那么问题就变形为了：我们有n+1种牌，每次取数量最多的n张牌进行数量减一的操作，问能操作多少次？

仔细想想，好像也不好做，那就再变形，问题又变形为：我们有n+1种牌，每次取数量最少的那张牌进行数量加一的操作，然后全部牌的数量均减一，问能操作多少次？

这样问题就迎刃而解了！【虽然貌似会超时部分点】

解法二：从侧面进行输出：
我们不一定要从正面进行贪心硬求套牌数目，很明显，这里求解的套牌数符合二分原理，于是考虑对套牌数进行二分答案：

如何判断？嗯很有意思。我们考虑我们当前二分到答案为u套套牌，我们设jl为要消耗的JOKER数量。那么我们只要枚举没一种牌，如果第i种牌的数量为ci，小于u，那么我们jl+=u-ci，相当于用JOKER将缺少的牌都补齐了。

最后我们再对jl进行判断，我们要满足两个条件：
1.用的JOKER数量不能超过总的JOKER数量
2.每套牌最多只能用一张JOKER

那么我们的jl同样只要满足两个条件：
1.jl小于等于JOKER的总数量M
2.jl小于等于我当前二分出来的答案u。因为如果我有u套牌，只用了jl(jl≤u)，那么就一定能找到一组解满足每套牌用的JOKER小于等于一张，这应该还是很好理解的吧。所以按照这样的思路直接二分答案就好了！

我打的是二分答案这种解法的，感兴趣的同学可以尝试一下解法一的打法。下面附上代码：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
long long a[5500];
long long i,j,k,m,n,o,p,js,jl,jk,l,r,mid;
long long pd(long long u)
{
    jl=0;
    for(int i=1;i<=n;i++)if(a[i]<u)jl+=u-a[i];

    if(jl<=m && jl<=u)return(true);
    else return(false);

}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
    l=0;r=2147483647;
    while(r-l>1)
    {
        mid=(l+r)/2;
        if(pd(mid))l=mid;
        else r=mid-1;
    }

    if(pd(r))printf("%lld",r);
    else printf("%lld",l);
    return 0;
}

C 这是一道大水题

问题描述：
给你N个数，非递减序列排序，有M次询问，每次询问一个区间[L，R]，问这个区间内出现最多的数的次数是多少？
输入格式
输入第一行包含一个数N。
第二行输入N个数。
第三行输入一个整数M。
接下来输入M行，每行两个整数L,R.
N<=100000，M<=100000
输出格式
这个区间内出现最多的数的次数是多少？
样例输入
10
1 2 3 3 4 4 5 5 6 6
5
1 3
4 8
3 8
3 7
1 10
样例输出
1
2
2
2
2

这道题很明显是一道区间的查询问题，我们同样提供两种比较相似的解法：

解法一：ST算法：
我们假如有一个原序列：
1 2 3 3 4 4 5 5 5 5
我们可以把它转化为a序列：
1 1 1 2 1 2 1 2 3 4

那么如果我们要查询[1,10]，问题就转化成了查询区间最值，但是这样就会出现一个问题，如果我们要查询[4,9]呢？这时有两个区间被斩断了，所以我们还要为维护一个序列，表示每一段区间有多长。

比如原序列：
4 4 4 4 5 5 6 6 6
我们就维护一个b序列：
4 4 4 4 2 2 3 3 3

这样的话还是上面那个例子，假如我们要查询[3,8],那么我们要查询的序列就是：
原序列：4 4 5 5 6 6
a序列：3 4 1 2 1 2
b序列：4 4 2 2 3 3

那么这个时候我们就可以把原序列分开两部分进行查询：
左部分：4 4
右部分：5 5 6 6

我们先看右部分如何操作，由于右部分都是完整的数字块或者完整的数字块的左部分，所以此时我们只要查询其对应部分的a序列的最大值就好了，蔽日我们现在得到的右部分的原序列：5 5 6 6对应的a序列为1 2 1 2，所以右部分的最大值为2。

接下来考虑如何快速得到左部分长度。由于左部分只含一种数字，所以其对应长度就为其开头点对应的b序列的值减去a序列的值再加一就是对应左部分的长度了，比如这个例子中，左部分长度就为4-3+1=2。

最后再比较左右部分答案取最大值就好了！

然后就很好操作了！【还是挺麻烦的说】

解法二：

既然觉得上面的算法复杂，我们就不如走回我们的老路——线段树，假如我们现在有一个数列，如下图：

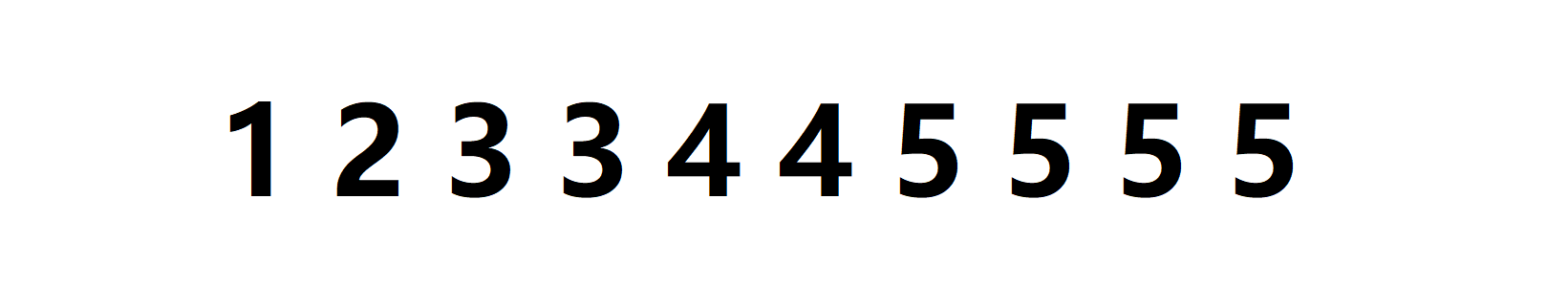
现在我们要查询[4,9],也就是被框起来的区间，我们发现这是由三大部分组成的：

不完整的数字块3，完整的数字块4，不完整的数字块5。

一头一尾所在的区间可能是不完整的，所以我们单独取出放在最后特判。我们现在要做的，就是用线段树再O(logn)的复杂度下，查询中间这一段完整区间相同数字的长度的最大值！

再比如：我们要查询区间[2,9]，这时我们线段树要做的就是查询完整的数字块2，3，4中相同数字长度的最大值，至于一头一尾，最后判断一下有没有中间找出来的最长数字串长度大就好啦。

最后附上代码：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;

struct node
{
    int l,r,max,num;
}tr[440000];

int a[110000],b[110000],c[110000],d[110000];
int i,j,k,m,n,o,p,js,jl,jk,ma,maa,x,y,xx,yy;

int my_min(int x,int y)
{
    if(x<y)return(x);
    else return(y);
}

int my_max(int x,int y)
{
    if(x>y)return(x);
    else return(y);
}
int build(int n,int l,int r)
{
    tr[n].l=l;tr[n].r=r;
    if(l==r)
    {
        tr[n].num=l;
        tr[n].max=b[l];
        return 0;
    }

    int mid=(l+r)/2;
    build(n*2,l,mid);
    build(n*2+1,mid+1,r);

    if(tr[n*2].max>tr[n*2+1].max)
    {
        tr[n].max=tr[n*2].max;
        tr[n].num=tr[n*2].num;
    }
    else
    {
        tr[n].max=tr[n*2+1].max;
        tr[n].num=tr[n*2+1].num;
    }
    return 0;
}
int fa(int u)
{
    int l=1,r=jl,mid;

    while(r-l>1)
    {
        mid=(l+r)/2;
        if(d[mid]>u)r=mid-1;
        else l=mid;
    }

    if(d[r]<=u)return(r);
    else return(r-1);
}

int find(int n,int l,int r)
{
    int mid=(l+r)/2;
    if(l>=xx+1 && r<=yy-1)
    {
        if(tr[n].max>ma)ma=tr[n].max;
        return 0;
    }
    if(xx+1<=mid)find(n*2,l,mid);
    if(yy-1>mid) find(n*2+1,mid+1,r);
    return 0;
}
int main()
{
    scanf("%d",&n);
    jl=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        if(a[i]>a[i-1])
        {
            jl++;
            c[jl]=a[i];
            d[jl]=i;
        }
        b[jl]++;
    }
    build(1,1,jl);

    scanf("%d",&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        xx=fa(x);
        yy=fa(y);
        ma=0;
        find(1,1,jl);
        if(my_min(d[xx+1],y+1)-x>ma)ma=my_min(d[xx+1],y+1)-x;
        if(y-my_max(d[yy],x)+1>ma)ma=y-my_max(d[yy],x)+1;
        printf("%d\n",ma);
    }
    return 0;
}

结语

这次的题目码量和难度都不会很大，关键是要有想法【我可能是个没什么想法的蒟蒻QwQ】。希望你能从中有所收获吧!最后希望你喜欢这篇BLOG！