今天在陈学康学长的指导下，了解并学习了k短路算法，发现也并没有想象中的那么难。那么这篇BLOG，就让我们一起来学习k短路算法吧！

什么是k短路

我们在之前的学习当中，肯定已经学习过了最短路算法，经典的求解最短路算法有SPFA和Dijkstra之类的，这这里就不再讲解了。今天我们要求解的如果不是最短路，而是第k短路怎么办？比如给你一道题：

给你一副有N个点(N≤1000)，M条边(M≤100000)的一个有向无负环图，问从1号点到N号点的第k短路的长度是多少。

比如在一幅图中，最短路为：

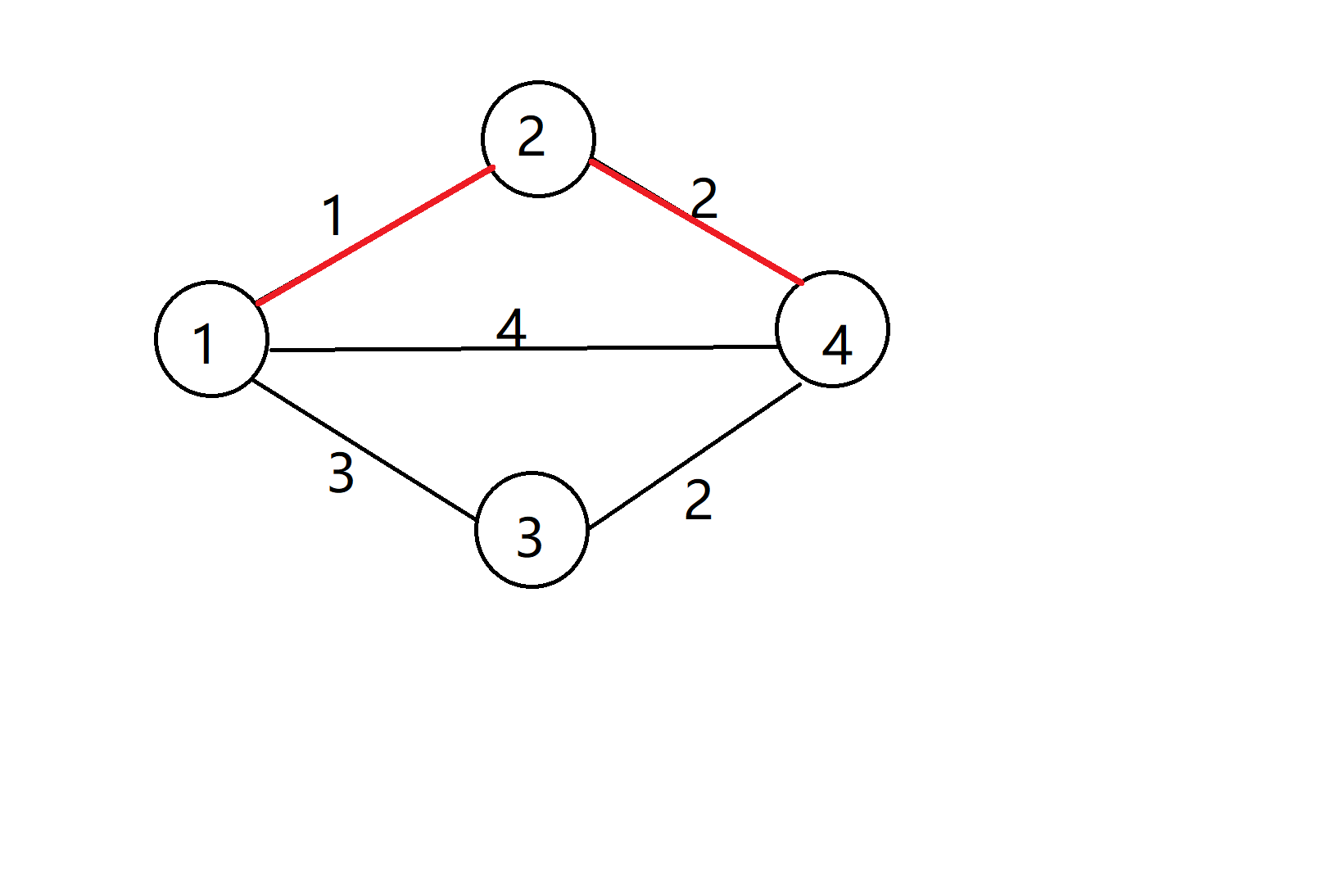
第2短路为：

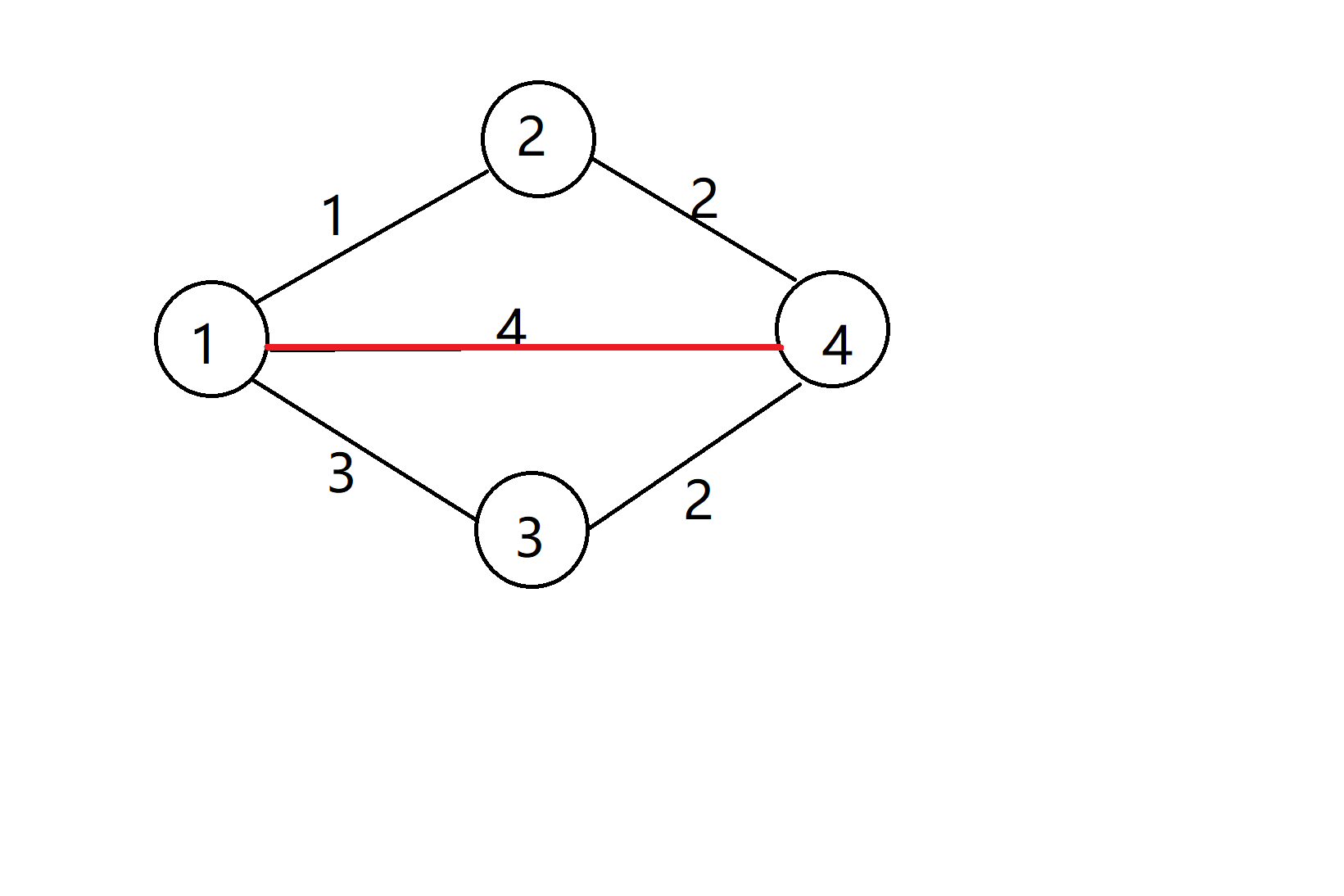
第3短路为：

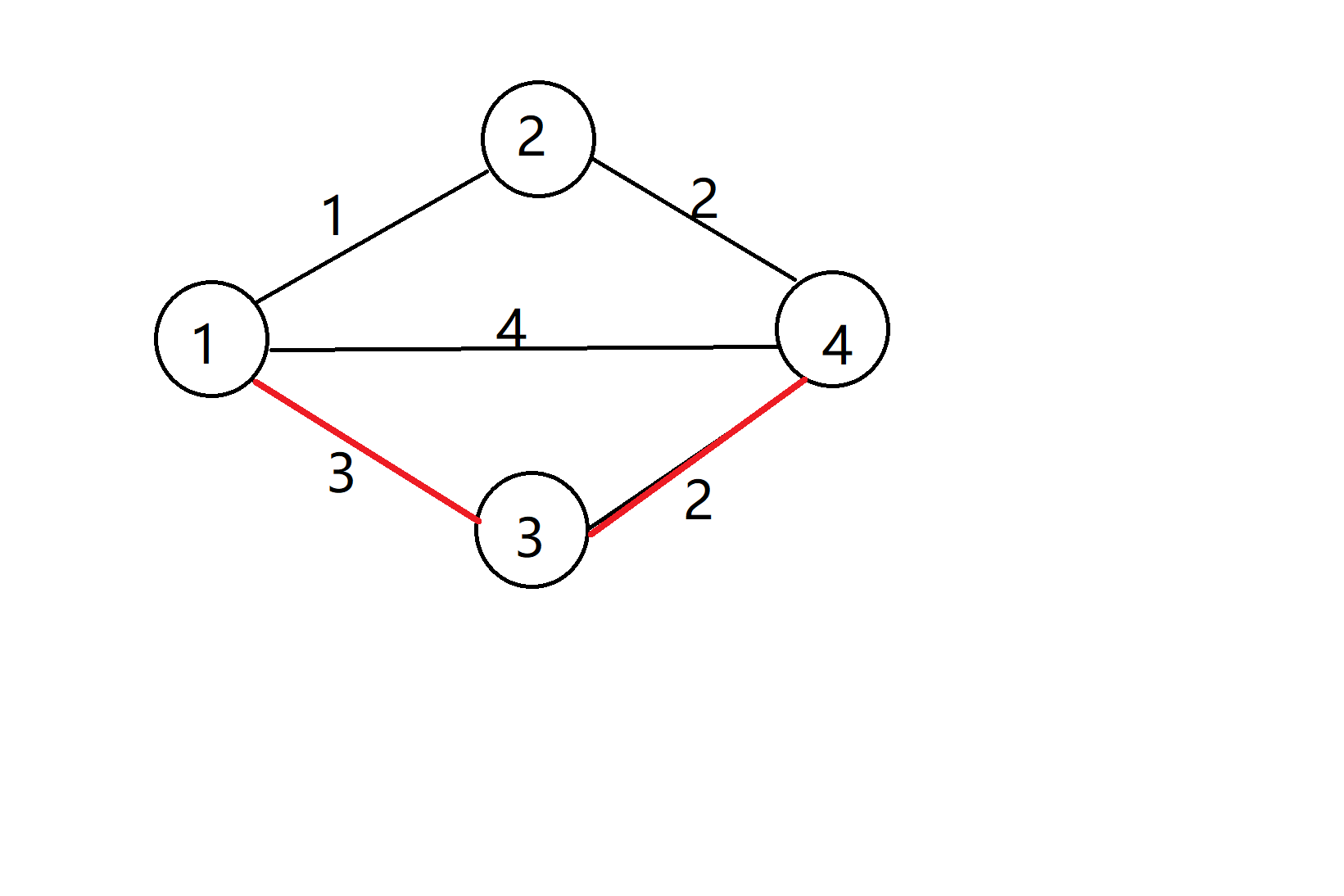
这道题的关键是如何求解第k短路。正常来说，最暴力的想，我们可以广搜出每一条从1到N的边，再进行排序就可以得到我们的解了。但是我们想一下，如果这样做时间复杂度先不谈，出现环了怎么办？这一切的障碍都促使我们优化上面的暴力算法，来在合理的时空范围内求解k短路问题。

考虑一下如果我们能在广搜的过程中知道优先拓展哪些点就好了。等一下？优先拓展某些点，对！你也和我一样想到了A*算法吧。

什么是A*算法

所谓A*算法就是启发是搜索，说白了就是给BFS搜索一个顺序使得搜索更加合理减少无谓的搜索。那么我们要如何来确定搜索的顺序？搜索的先后顺序可以用一个值来表示，我们一般称这个值为h[x]，我们每次搜索都取h[x]最小的点进行拓展。

一般来说，h[x]由两个参数组成——f[x]与g[x]。其中h[x]=f[x]+g[x]其中这个f[x]就是当前搜索时的代价，而g[x]是一个估价函数，估价函数代表的是对当前点到目标的代价的估计，而这个估计必须小于等于实际值，否则会出现奇奇怪怪的错误，在A*算法中，最重要也是最玄学的一步就是构造g[x]。

怎样求解k短路

此时，我们就可以考虑用A*算法为底层来计算k短路了。

我们在这里介绍的只是求K短路一种方法，就是用正向的BFS A*算法和反向的最短路算法来求解第k短路的长度。在这里，g[x]的设定为到这个点到目标点的最短路径,显然这个估价函数其实小于等于实际值的，f[x]就是从开始时，搜索到这个点时所用的代价。

我们可以用一个优先队列来维护f[x]+g[x],每次取出f[x]+g[x]最小的点来拓展，拓展也就是通过当前队列头的点来更新其能直接经过一条边到达的点，这里如果更新了一个不在队列里就丢进优先队列里去，反正每次总会从队首弹出h[x]+g[x]最小的点。

我们可以想一下，如果当前取出的优先队列头是我们要到的结束点t并且是第一次取出，那么就找到了一条从源点s到结束点t的最短路径。这里其实很djikstra的感觉有点像，如果第二次在队头发现了呀，又是结束点t，则是找到了一条从源点s到结束点t的第二短路径也就是次短路……依次类推，第k次从队头弹出我们的结束点t，就找到了从源点s到结束点t的第k短路径。

那要是这幅图本身就不存在K短路呢？？那就是结束点t拓展不到K次但是其他点很有可能一直打圈圈无限下去.，比如下面这副图：

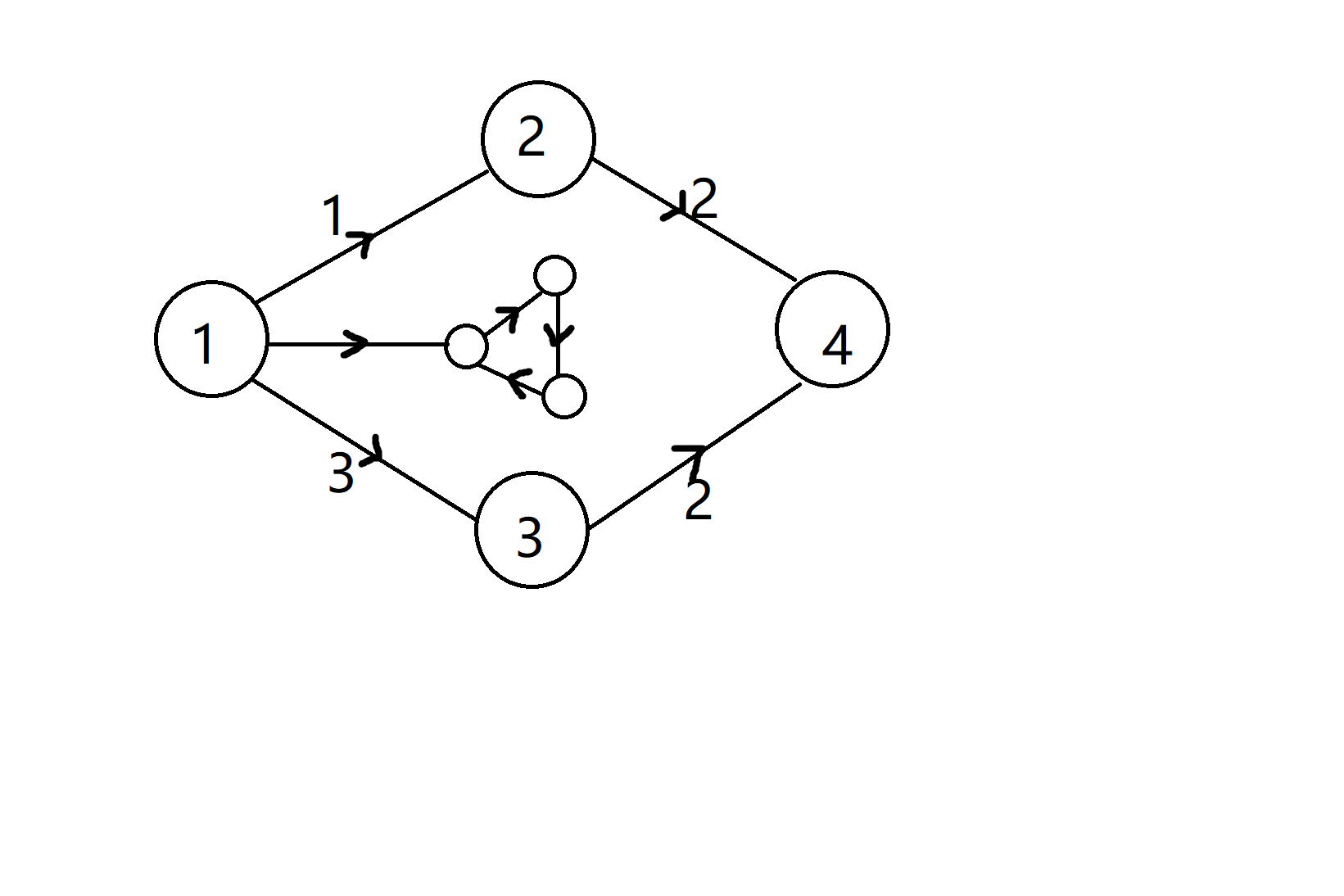
如果要求第3短路，不加特判的话，由于一直无法第三次拓展到结束点，所以程序就会一直在中间那个环转圈圈。

所以这里就要用个条件来判断一下，首先在找某个点作为优先队列头出现了几次就用了一个计数器time[]，所求的点time[t]==k就代表得到了第k短路。如果当前想拓展的点time[]>k就没必要继续拓展了，因为这个点已经是求到k+1短路了，从这个点继续往下搜肯定得到的是大于等于k+1短路的路径，就没有必要继续拓展了。

程序实现方法

下面我们就来实现一下k短路算法。首先我们要定义一个优先队列，这里我们可以用STL库里的优先队列：

声明   #include<queue>
定义   priority_queue<类型> 变量名 
但注意的是若是对结构体用..则需要在结构体中对 < 进行重载...如这道题的struct就应该写成这样:

接着就要反向跑一遍SPFA，在SPFA当中我们还用到了SLF优化，那么什么是SLF优化呢？

SPFA算法有两个优化算法 SLF 和 LLL：
SLF：Small Label First 策略，设要加入的节点是j，队首元素为i，若dist(j) < dist(i)，则将j插入队首，否则插入队尾。
LLL：Large Label Last 策略，设队首元素为i，每次弹出时进行判断，队列中所有dist值的平均值为x，若dist(i)>x则将i插入到队尾，查找下一元素，直到找到某一i使得dist(i)<=x，则将i出对进行松弛操作。

程序如下：

int spfa(int s,int t)//正向SPFA
{
    memset(vis,0,sizeof(vis));//vis数组记录某一个点是否在队列中 
    for(int i=1;i<n;i++)g[i]=0x7fffffff;//g[i]表示i点到结束点的最短路径长度 

    q.push_back(t);vis[t]=1;//将结束点塞进队列，设置为访问过 

    while(!q.empty())//只要队列不空 
    {
        x=q.front();q.pop_front();//取出队首元素进行操作 
        for(int k=lastt[x];k;k=b[k].next)
        {
            y=b[k].y;
            if(b[k].s+g[x]<g[y])
            {
                g[y]=(b[k].s+g[x]);
                if(vis[y]==0)
                {
                    vis[y]=1;
                     if(!q.empty() && g[y]<g[q.front()])q.push_front(y);
                     else q.push_back(y);//SLF优化 
                }
             } 
        }
        vis[x]=0;//队首退队，设为未访问 
    }
    return(0);
} 

正向来一遍A*算法:

int astar()//正向A*算法 
{
    while (!p.empty()) p.pop();//先清空一下队列 
    node temp,o;
    temp.p=s;temp.f=0;temp.g=0;
    p.push(temp);//队首插入源点 

    while(!p.empty())//队首不空 
    {
        o=p.top();
        p.pop();x=o.p;//访问队首 

        time[x]++;// 访问次数+1 

        if(x==t && time[x]==k)
        {
            return(o.f);
        }//结束点访问次数为k时，结束程序返回k短路长度 

        if(time[x]>k)continue;//不访问已经访问了k次以上的点 

        for(int k=last[x];k;k=a[k].next)
        {
            temp.p=a[k].y;
            temp.f=a[k].s+o.f;
            temp.g=g[a[k].y];
            p.push(temp);
        }//插入新的拓展点 

    }
    return(0);

}

到这里，k短路算法的主体就结束了。

经典例题

[luogu P2483] 【模板】k短路（[SDOI2010]魔法猪学院）

题目描述
iPig在假期来到了传说中的魔法猪学院，开始为期两个月的魔法猪训练。经过了一周理论知识和一周基本魔法的学习之后，iPig对猪世界的世界本原有了很多的了解：众所周知，世界是由元素构成的；元素与元素之间可以互相转换；能量守恒……。

能量守恒……iPig 今天就在进行一个麻烦的测验。iPig 在之前的学习中已经知道了很多种元素，并学会了可以转化这些元素的魔法，每种魔法需要消耗 iPig 一定的能量。作为 PKU 的顶尖学猪，让 iPig 用最少的能量完成从一种元素转换到另一种元素……等等，iPig 的魔法导猪可没这么笨！这一次，他给 iPig 带来了很多 1 号元素的样本，要求 iPig 使用学习过的魔法将它们一个个转化为 N 号元素，为了增加难度，要求每份样本的转换过程都不相同。这个看似困难的任务实际上对 iPig 并没有挑战性，因为，他有坚实的后盾……现在的你呀！

注意，两个元素之间的转化可能有多种魔法，转化是单向的。转化的过程中，可以转化到一个元素（包括开始元素）多次，但是一但转化到目标元素，则一份样本的转化过程结束。iPig 的总能量是有限的，所以最多能够转换的样本数一定是一个有限数。具体请参看样例。

输入输出格式
输入格式：
第一行三个数 N、M、E 表示iPig知道的元素个数（元素从 1 到 N 编号）、iPig已经学会的魔法个数和iPig的总能量。

后跟 M 行每行三个数 si、ti、ei 表示 iPig 知道一种魔法，消耗 ei 的能量将元素 si 变换到元素 ti 。

输出格式：
一行一个数，表示最多可以完成的方式数。输入数据保证至少可以完成一种方式。

输入输出样例
输入样例#1：
4 6 14.9
1 2 1.5
2 1 1.5
1 3 3
2 3 1.5
3 4 1.5
1 4 1.5
输出样例#1：
3

说明
有意义的转换方式共4种：
1->4，消耗能量 1.5
1->2->1->4，消耗能量 4.5
1->3->4，消耗能量 4.5
1->2->3->4，消耗能量 4.5

显然最多只能完成其中的3种转换方式（选第一种方式，后三种方式仍选两个），即最多可以转换3份样本。

如果将 E=14.9 改为 E=15，则可以完成以上全部方式，答案变为 4。

数据规模

占总分不小于 10% 的数据满足 N <= 6，M<=15。

占总分不小于 20% 的数据满足 N <= 100，M<=300，E<=100且E和所有的ei均为整数（可以直接作为整型数字读入）。

所有数据满足 2 <= N <= 5000，1 <= M <= 200000，1<=E<=107，1<=ei<=E，E和所有的ei为实数。

OK,这是一道NOI+/CTSC难度的题目，什么不信？

我们先用一道普通题的眼光去观望一下这道题。欸不是很简单，不断找最短路，次短路，第三短路……吧长度不断累加，直到大于总能量值。

这样直接写的话，就恭喜你TLE了，而且只拿到了4个点。

至于为什么超时就比如：

在中间过程中已经到达了某个点K次，第K+1次到达时去终点最少也是K+1短的，因为光是从这个点就出去了K次了。所以K+1以及之后到这个点就没必要再向终点去了，去了也排不到前K，还多连出好多路径方案来占空间造成MLE。

k如何确定呢？总能量值除以最短路长度不就是k最大的值了吗？然后就在A*和SPFA中加一些你能想到的所有优化这题就就能拿到92分了：

// luogu-judger-enable-o2
#include<queue> 
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
    int p;double f,g;
    bool operator < (const node &a) const
    {
        return a.f+a.g<f+g;
    }
};
struct nodee
{
    int x,y,next;double s;
}a[220000],b[220000];

priority_queue <node> p; 
deque <int> q;
int i,j,k,m,n,o,js,jl,jk,x,y,ans,len=0,lenn=0,s,t;
double f[5500],g[5500];
int vis[5500],last[5500],lastt[5500],time[5500];

double ma,z,ddq=0,kk;

int read()//一个随处可见的读优
{
    int z=0,f=1;char k;
    while(k<'0'||k>'9'){if(k=='-')f=-1;k=getchar();}
    while(k>='0'&&k<='9'){z=(z<<3)+(z<<1)+k-'0';k=getchar();}
    return z*f;
}

void ins(int x,int y,double z)
{
    len++;
    a[len].x=x;a[len].y=y;a[len].s=z;
    a[len].next=last[x];
    last[x]=len;
}

void inss(int x,int y,double z)
{
    lenn++;
    b[lenn].x=x;b[lenn].y=y;b[lenn].s=z;
    b[lenn].next=lastt[x];
    lastt[x]=lenn;
}

int spfa(int s,int t)//正向SPFA
{
    memset(vis,0,sizeof(vis));//vis数组记录某一个点是否在队列中 
    for(int i=1;i<n;i++)g[i]=0x7fffffff;//g[i]表示i点到结束点的最短路径长度 

    q.push_back(t);vis[t]=1;//将结束点塞进队列，设置为访问过 

    while(!q.empty())//只要队列不空 
    {
        x=q.front();q.pop_front();//取出队首元素进行操作 
        for(int k=lastt[x];k;k=b[k].next)
        {
            y=b[k].y;
            if(b[k].s+g[x]<g[y])
            {
                g[y]=(b[k].s+g[x]);
                if(vis[y]==0)
                {
                    vis[y]=1;
                     if(!q.empty() && g[y]<g[q.front()])q.push_front(y);
                     else q.push_back(y);//SLF优化 
                }
             } 
        }
        vis[x]=0;//队首退队，设为未访问 
    }
    return(0);
} 

int astar()
{
    while (!p.empty()) p.pop();
    node temp,o;
    temp.p=s;temp.f=0;temp.g=0;
    p.push(temp);

    while(!p.empty())
    {
        o=p.top();
        p.pop();x=o.p;

        time[x]++;

        if(o.f+o.g+ddq>ma)return(0);
        if(x==t)
        {
            ddq+=o.f,ans++;
            continue;
        }

        if(time[x]>kk)continue;

        for(int k=last[x];k;k=a[k].next)
        {
            temp.p=a[k].y;
            temp.f=a[k].s+o.f;
            temp.g=g[a[k].y];
            p.push(temp);
        }

    }
    return(0);

}
int main()
{
    n=read();m=read();
    scanf("%lf",&ma);
    s=1;t=n;
    for(int i=1;i<=m;i++)
    {
        x=read();y=read();
        scanf("%lf",&z);
        ins(x,y,z);inss(y,x,z);
    }
    ans=0;
    spfa(s,t);
    kk=ma/g[1];
    astar();
    printf("%d",ans);

    return 0;
}

然后莫名其妙的TLE了一个点，大概是这样的：

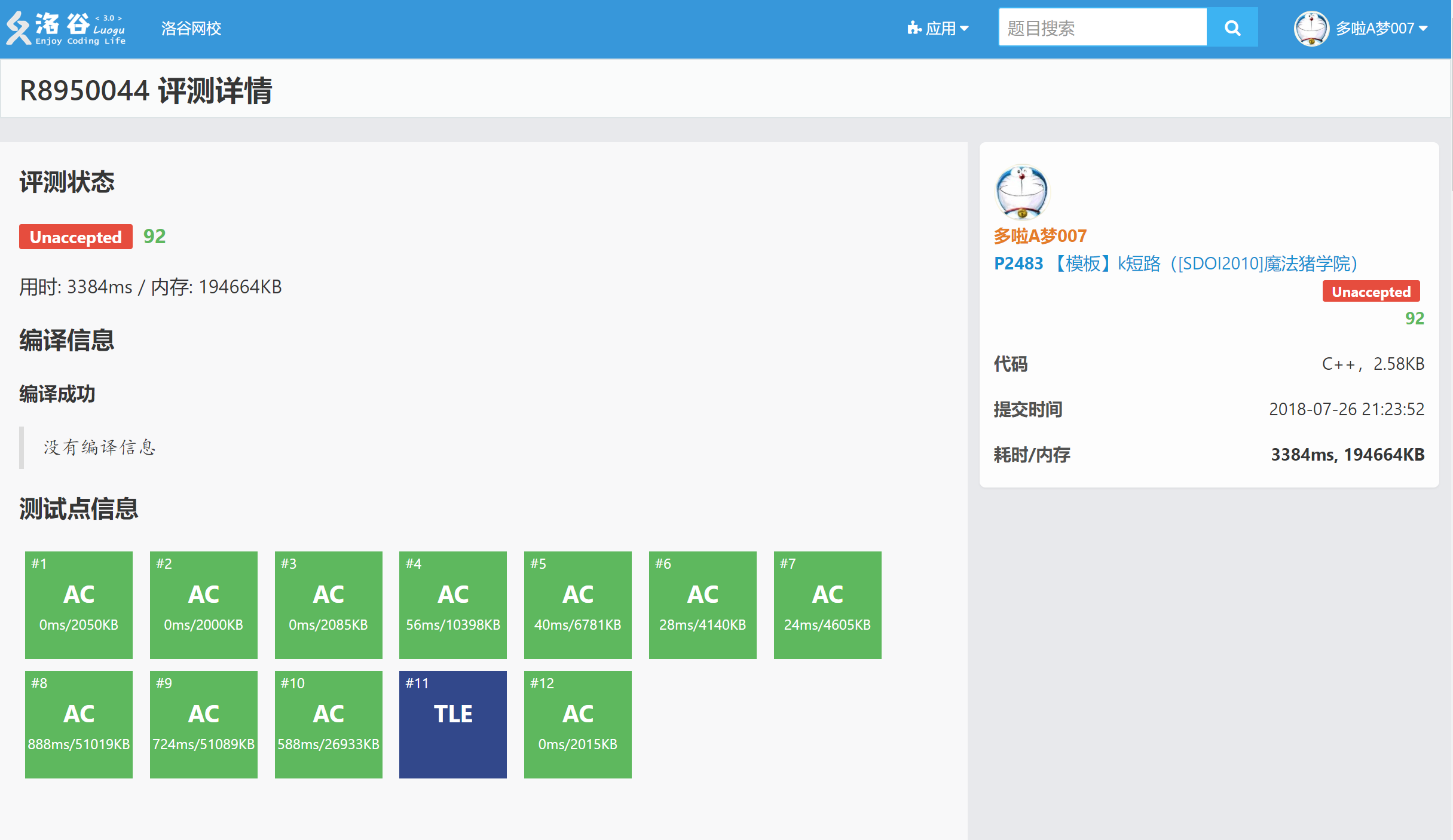
然后我嫩头青的调试了一个上午，还是卡在92……这怕是NOI+的真正原因：

然后带着敬畏的心态去看了一下AC大佬们的程序，发现从第二个AC的人开始都加了一段神秘代码：

if(ma==10000000)
    {
        printf("2002000\n");
        return 0;
    }

然后就AC了……至于第一个人，复制它的程序上交发现放在今天的数据，它的程序是会WA的，所以对于这种神题……也就只能当作自己过了吧……

结语

通过这篇BLOG，相信你已经学会了如何写k短路算法，并且可以AC一道NOI+/CTSC难度的题目了（滑稽）。希望你喜欢这篇BLOG！