在之前的BLOG里，我们谈论过了二分图的一部分问题——最大匹配问题，并且一起学习了解决这类问题的匈牙利算法，还没有学过的同学可以 点击我学习最大匹配算法。在这一篇BLOG里，我们将一同学习二分图的另一个问题——最大带权匹配问题。

什么是二分图最大带权匹配

那么什么是二分图的最大带权匹配呢？实现我们都应该知道什么是二分图的最大匹配。不知道也没关系，我们先看一下下面这个问题：比如我们有3个公牛和3个母牛，有几对公牛何和几对公牛互相喜欢，但是一只母牛只能和一只公牛在一起，问最多能配成几对互相喜欢的情侣？

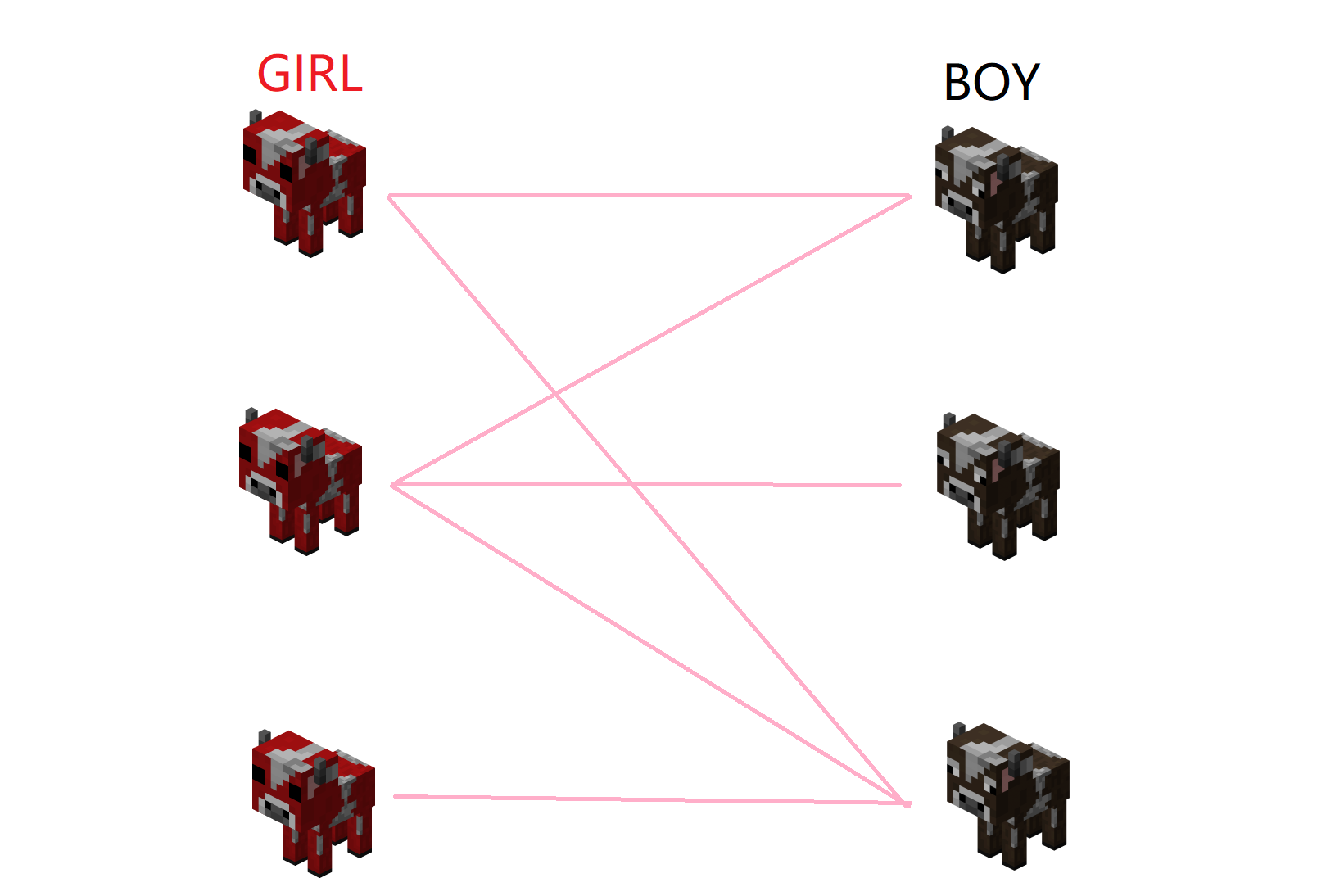
在这道题，要我们求的就是最大匹配数，很明显，最大匹配数为3，而且有多组解，下面就给出一种解，我们把选出来的匹配用红色代替：

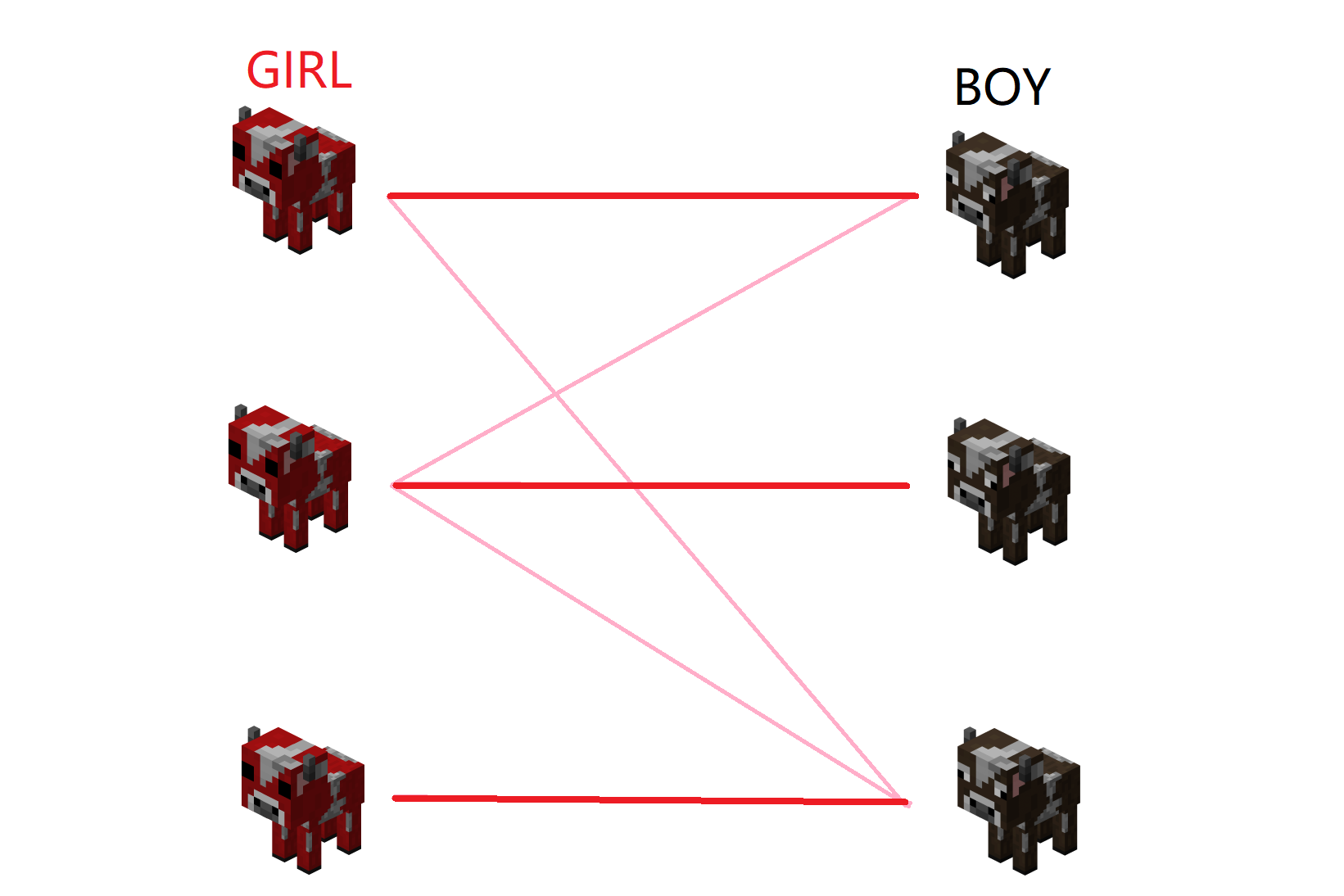
好的现在我们把问题升级一下，如果第i对互相喜欢的牛如果在一起就会获得一个幸福值d[i]，但是一只母牛仍然只能和一只公牛在一起，那么要如何配对，才能让匹配后幸福值之和最高？

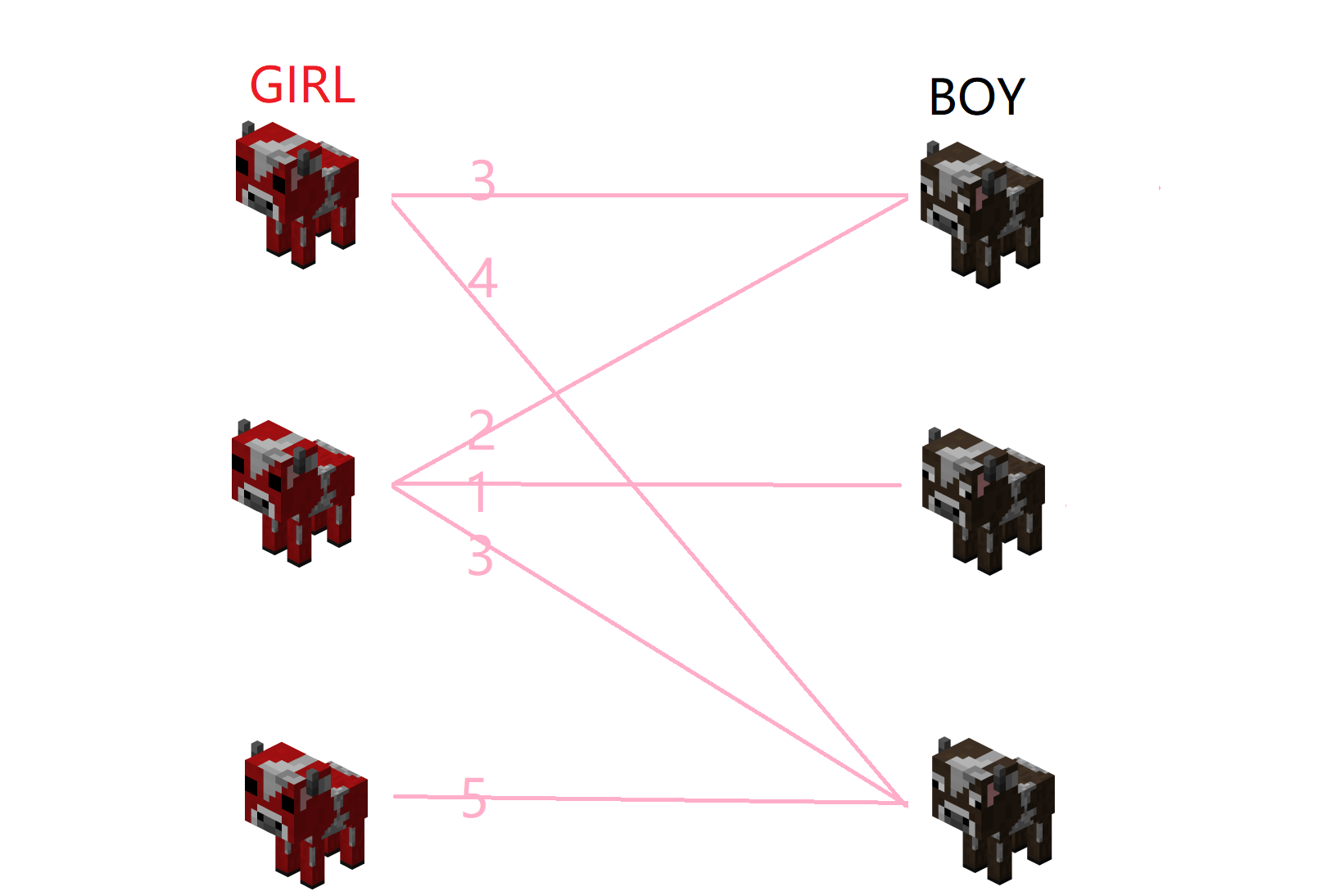
这就是我们这一次要讨论的二分图最大带权匹配问题了。

KM算法具体实现方法详解

下面我们就继续沿着上面的例子，继续使用上面的几只牛，讲解一下KM算法是如何操作的吧。

我们要怎么选择最优的配对方法呢？

首先，每只母牛都会有一个期望值，就是与她有好感的公牛中能得到的最大幸福值。公牛呢，期望值为0，换一种方式来说。只要随便有一个母牛就可以啦。

这样，我们把每只牛的期望值标出来。

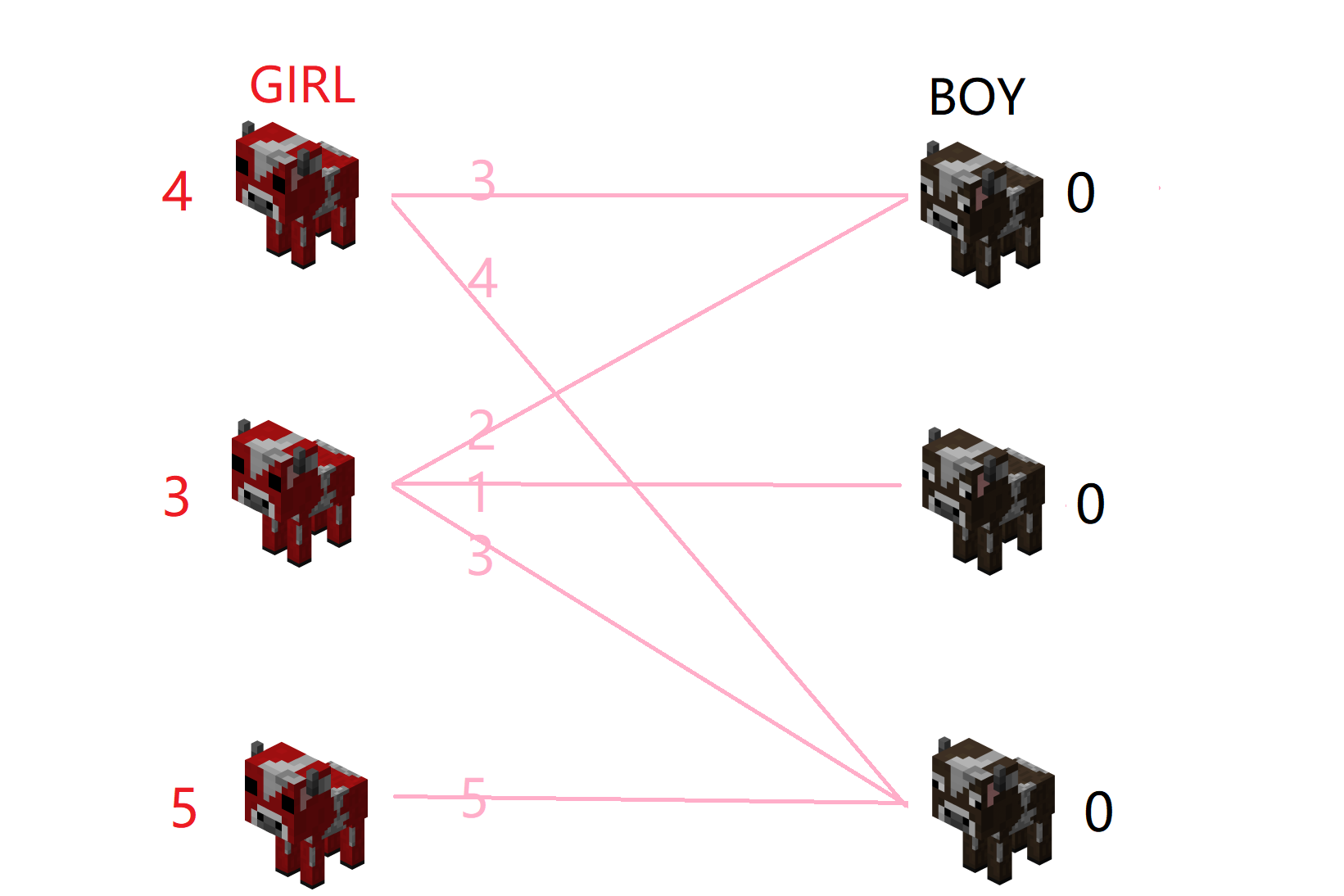
接下来，对母牛逐个开始配对。

我们看看配对方法：

我们从第一只母牛开始，分别为每一只母牛找对象。

每次都从第一只公牛开始，选择一只公牛，使两只牛的期望和要等于两人之间的好感度。

注意：每一轮匹配，每只公牛只会被尝试匹配一次！

下面我们来展示具体的匹配过程：

为1号母牛找对象

母牛1开始找对象

（此时还没有公牛匹配成功，也就是说这种母牛可以找自己最喜欢的公牛，和他一起***）

根据上面所提到的 “公母两头牛的期望和要等于两头牛之间的好感度”的规则：

母牛1-公牛1：4+0 != 3
母牛1-公牛3：4+0 == 4

所以母牛1选择了公牛3，母牛1找对象成功。

母牛1找对象成功

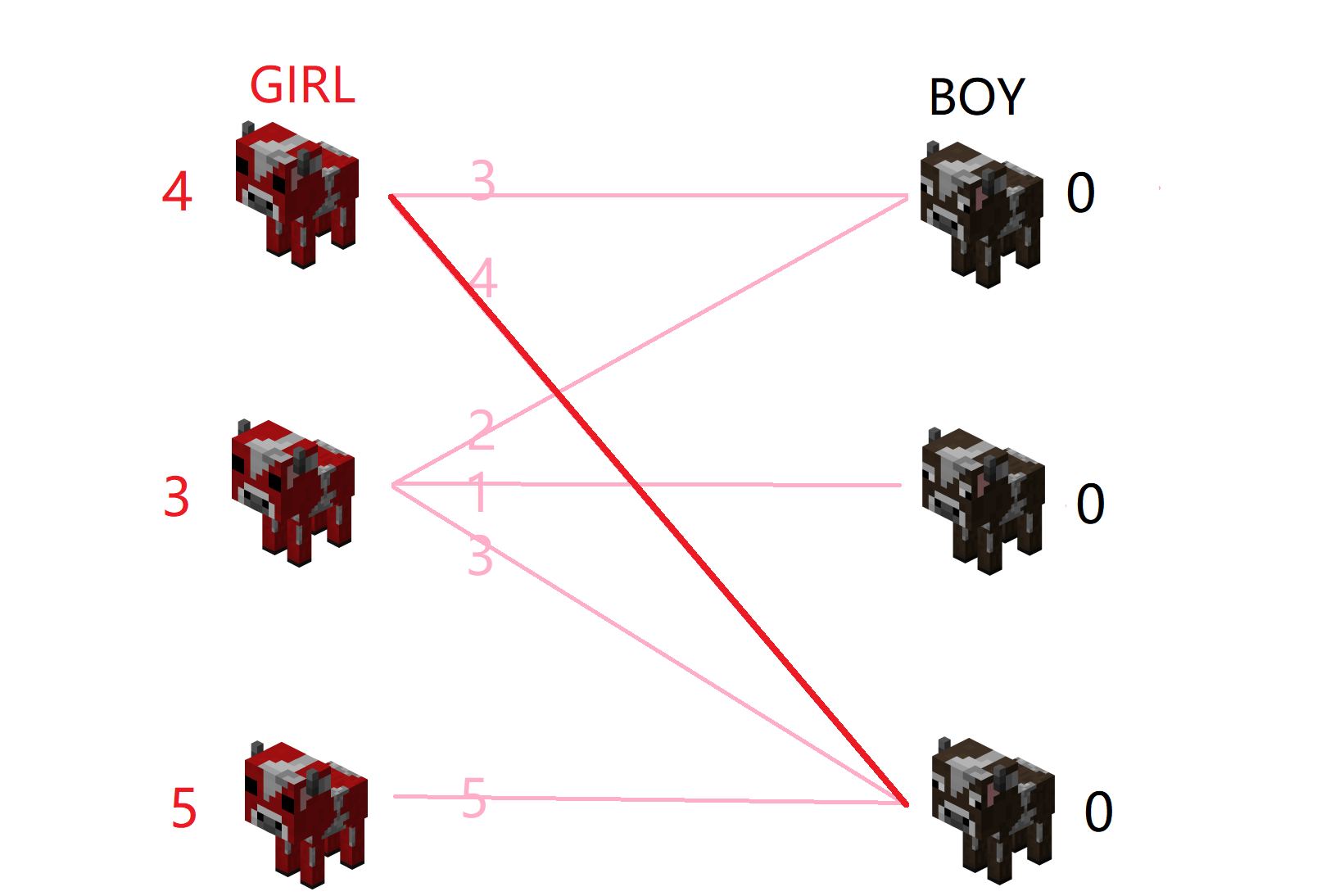
找到心仪对象后，母牛1很开心。

为2号母牛找对象

母牛2开始找对象

（此时母牛1—公牛3已经匹配成功）

根据配对原则 ——“公母两头牛的期望和要等于两头牛之间的好感度”：

公牛3已经有了女朋友——母牛1，我们就问问在满足规则的前提下，母牛1能不能换一只公牛呢？

我们尝试让母牛1去找别人……

尝试失败……

为女2找对象失败！

我们发现，这一轮参与匹配的人有：母牛1，母牛2，公牛3。

那现在呢怎么办？？？很容易想到的，这两只母牛只能降低一下期望值了，降低多少呢？

很显然地，期望值下降的值应该是——任意一个参与匹配母牛能换到任意一个这轮没有被选择过的公牛所需要降低的最小值。

比如：若母牛1选择公牛1，则期望值要降低1。 母牛2选择公牛1，期望值要降低1。 母牛2选择公牛2，期望值要降低2。

于是，只要期望值降低1，就有母牛可能选择其他人。所以这轮出现过的母牛们的期望值要降低1点。

同时，刚才被抢的公牛们此时非常得意，因为有一群母牛来抢他，于是他的期望值提高了1点（就是同母牛们降低的期望值相同）。

于是期望值变成这样（当然，不参与刚才匹配过程的牛期望值不发生改变）

继续为母牛2找对象

（此时母牛1—公牛3匹配成功）

根据现在的匹配规则，母牛2可以选择公牛1，于是母牛2选择了公牛1。

并且母牛2惊讶的发现：公牛1还没有被配对

母牛2找对象成功！

母牛2找对象成功

母牛2成功与公牛2匹配，它很开心。

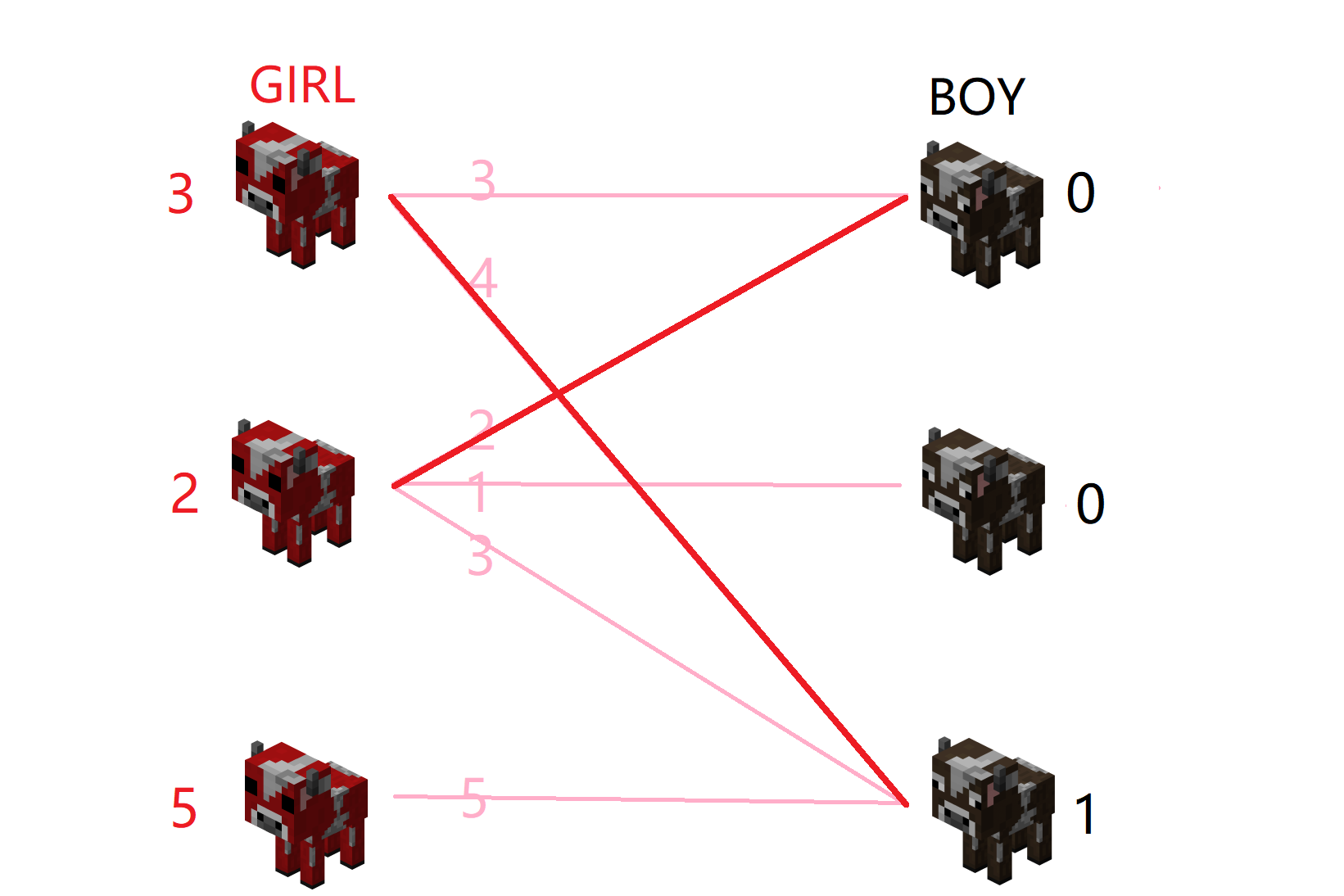
为母牛3找对象

开始为女3找对象

（此时母牛1—公牛3，母牛2-公牛1）

根据配对规则—— “公母两头牛的期望和要等于两头牛之间的好感度”母牛3没有可以配对的公牛……

母牛3找对象失败

母牛3找对象失败

在这一轮中至今只有母牛3参与匹配

此时应该为母牛3降低期望值

降低期望值1的时候，母牛3-公牛3可以配对，所以母牛3降低期望值1

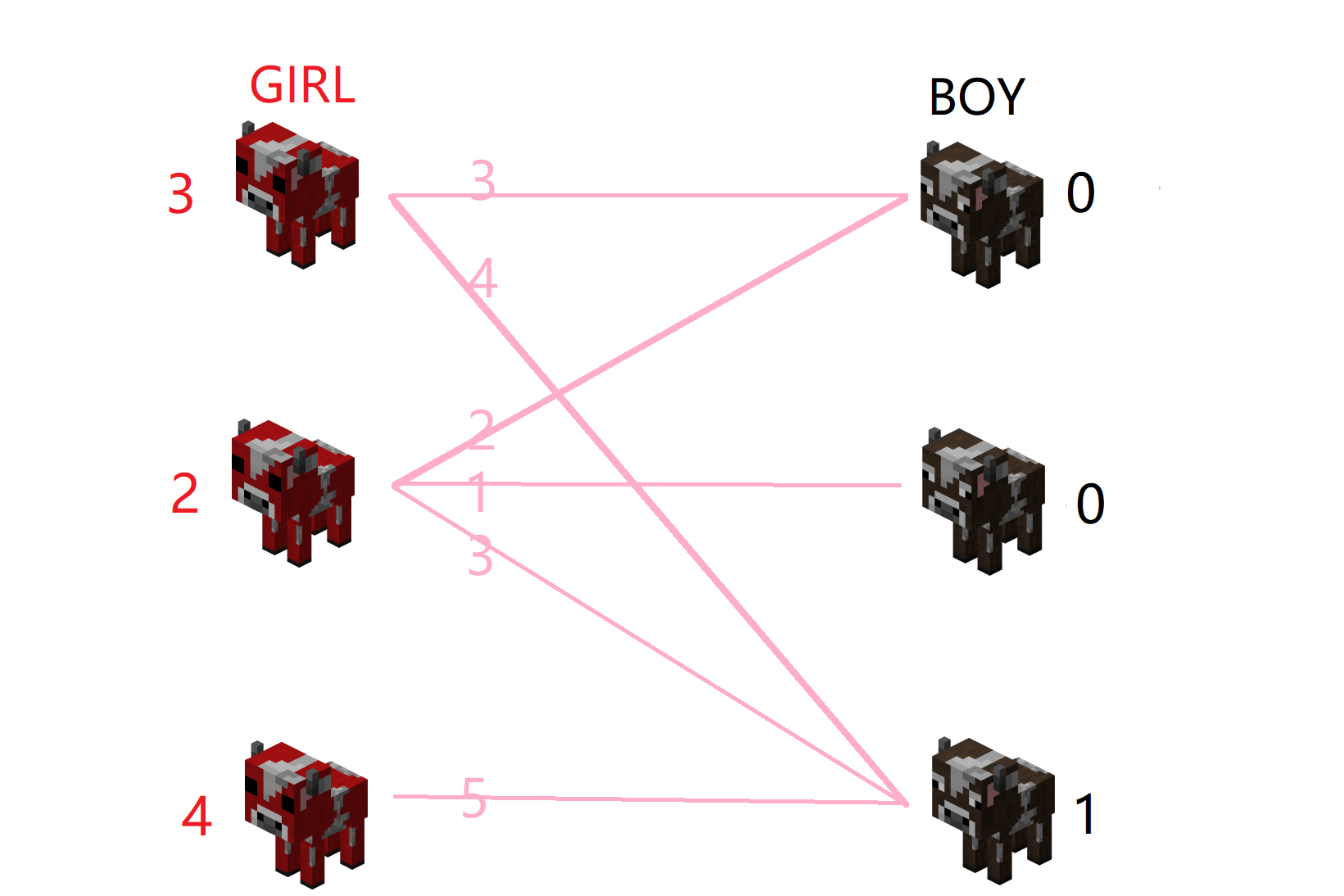
继续为母牛3找对象

（此时母牛1—公牛3， 母牛2-公牛1）

在降低期望值以后，公牛3成了母牛3唯一值得喜欢的公牛

但此时公牛3已经有女朋友-母牛1，于是母牛1尝试换人

根据配对规则，母牛1选择公牛1

而公牛1也已经有了女朋友-母牛2，母牛2尝试换人

前面说过，每一轮匹配每个男生只被匹配一次，所以母牛2无法访问公牛3

所以母牛2换人失败

母牛3找对象再次失败

母牛3找对象再次失败

我们来看一下这一轮匹配相关的牛：母牛1，母牛2，母牛3，公牛1，公牛3

此时，只要母牛2降低1点期望值，就能换到男2，所以我们对所有访问过的母牛期望值降低1，公牛上升1

（前面提过 降低的值x=任意一个母牛能换到任意一个没有被选择过的公牛所需要降低的最小值）

这时我们把相应人员期望值改变一下

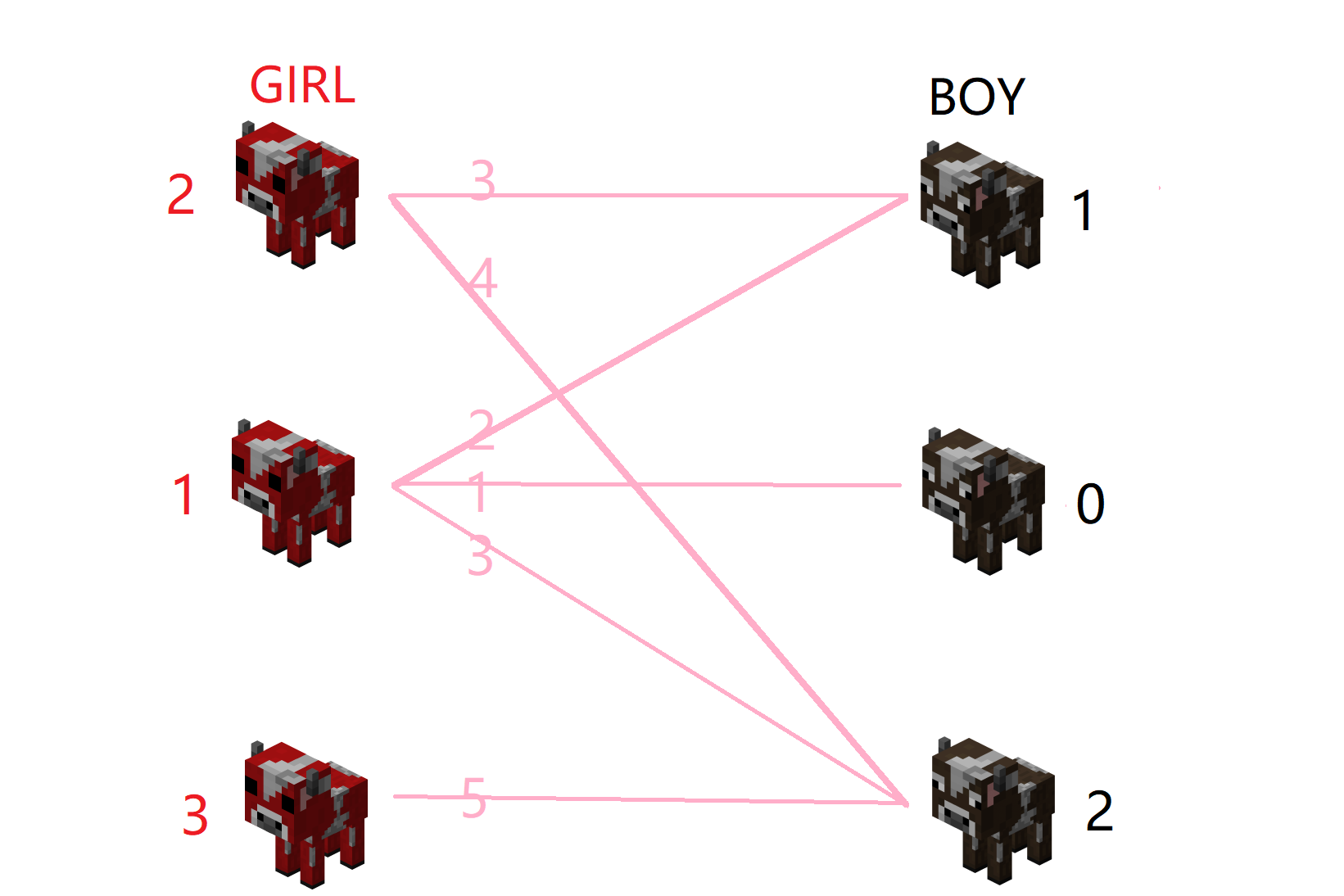
还是为女3找对象

（此时母牛1—公牛3， 母牛2-公牛1）

母牛3选择了公牛3

但此时公牛3已经有女朋友-母牛1，于是母牛1尝试换人

根据配对规则，母牛1选择公牛1

而公牛1也已经有了女朋友-母牛2，母牛2尝试换人

母牛2换公牛2

公牛2无主，匹配成功！！！

为女3找对象成功

匹配成功，完结撒花~~

到此匹配全部结束

此时

母牛1-母牛1，母牛2-公牛2，母牛3-公牛3

幸福值和为最大：9

KM算法的程序实现

虽然在上面看来，这样的配对非常复杂，但是其实在题目当中，只要简单的循环匹配的处理就好了。

直接来到模板题吧：

[hdu p2255]奔小康赚大钱

Problem Description
传说在遥远的地方有一个非常富裕的村落,有一天,村长决定进行制度改革：重新分配房子。
这可是一件大事,关系到人民的住房问题啊。村里共有n间房间,刚好有n家老百姓,考虑到每家都要有房住（如果有老百姓没房子住的话，容易引起不安定因素），每家必须分配到一间房子且只能得到一间房子。
另一方面,村长和另外的村领导希望得到最大的效益,这样村里的机构才会有钱.由于老百姓都比较富裕,他们都能对每一间房子在他们的经济范围内出一定的价格,比如有3间房子,一家老百姓可以对第一间出10万,对第2间出2万,对第3间出20万.(当然是在他们的经济范围内).现在这个问题就是村领导怎样分配房子才能使收入最大.(村民即使有钱购买一间房子但不一定能买到,要看村领导分配的).

Input
输入数据包含多组测试用例，每组数据的第一行输入n,表示房子的数量(也是老百姓家的数量)，接下来有n行,每行n个数表示第i个村名对第j间房出的价格(n<=300)。

Output
请对每组数据输出最大的收入值，每组的输出占一行。

Sample Input
2
100 10
15 23

Sample Output
123

这很显然就是一道裸的KM算法，我们把老百姓当成母牛，房子当成公牛，用矩阵存储，就好了，模板接上：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;

int love[330][330];// 记录每个母牛和每个公牛的好感度
int ex_girl[330];// 每个母牛的期望值
int ex_boy[330];// 每个公牛的期望值
bool vis_girl[330];// 记录每一轮匹配匹配过的母牛 
bool vis_boy[330];// 记录每一轮匹配匹配过的公牛 
int match[330];// 记录每个公牛匹配到的母牛 如果没有则为-1
int slack[330];// 记录每个公牛如果能被母牛倾心最少还需要多少期望值
int n;

int my_max(int x,int y)//比较，返回较大值 
{
    if(x>y)return x;
    else return(y);
}

int my_min(int x,int y)//比较，返回较小值 
{
    if(x<y)return(x);
    else return(y);
}

bool dfs(int girl)//查找这个母牛是否脱单 
{
    vis_girl[girl]=false;
    for(int i=1;i<=n;i++)
    {
        if(vis_boy[i]==true)// 每一轮匹配 每个公牛只尝试一次
        {
            int gap=ex_boy[i]+ex_girl[girl]-love[girl][i];
            if(gap==0)// 如果符合要求
            {
                vis_boy[i]=false;
                if(match[i]==-1 || dfs(match[i])==true)// 找到一个没有匹配的公牛
                // 或者该公牛之前匹配好的的母牛可以找到其他人
                {
                    match[i]=girl;
                    return(true);
                }
            }
            else
            {
                slack[i]=my_min(slack[i],gap);// slack 可以理解为该公牛要得到母牛的倾心 
                //还需多少期望值 取最小值 就是先要当作备胎的样子0vo 
            }
        }
    }
    return(false);
}

int KM()
{
    memset(match,-1,sizeof(match));// 初始每个公牛都没有匹配的母牛 
    memset(ex_boy,0,sizeof(ex_boy));// 初始每个公牛的期望值为0

    for(int i=1;i<=n;i++)ex_girl[i]=love[i][1];
    for(int i=1;i<=n;i++)
    for(int j=2;j<=n;j++)
    ex_girl[i]=my_max(ex_girl[i],love[i][j]);

    // 每个母牛的初始期望值是与她相连的公牛最大的好感度

    for(int i=1;i<=n;i++)// 尝试为每一只母牛解决归宿问题
    {
        memset(slack,63,sizeof(slack));// 因为要取最小值 初始化为无穷大
        while(1)
        {
            // 为每只母牛解决归宿问题的方法是 ：如果找不到就降低期望值，直到找到为止
            memset(vis_boy,true,sizeof(vis_boy));
            memset(vis_girl,true,sizeof(vis_girl));

            if(dfs(i)==true)break;// 找到归宿 退出

            // 如果不能找到 就降低期望值
            // 最小可降低的期望值

            int d=2147483640;
            for(int j=1;j<=n;j++)
            if(vis_boy[j]==true)d=my_min(d,slack[j]);

            for(int j=1;j<=n;j++)
            {
                if(vis_girl[j]==false)ex_girl[j]-=d;// 所有访问过的母牛降低期望值

                if(vis_boy[j]==false)ex_boy[j]+=d;// 所有访问过的公牛增加期望值
                else slack[j]-=d;
                // 没有访问过的boy 因为girl们的期望值降低，距离得到母牛倾心又进了一步！
            }
        }
    }
    // 匹配完成 求出所有配对的好感度的和
    int res=0;
    for(int i=1;i<=n;i++)res+=love[match[i]][i];
    return(res);
}

int main()
{
    while(scanf("%d",&n)!=EOF)
    {
        for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        scanf("%d",&love[i][j]);

        printf("%d\n",KM());
    }
    return 0; 
} 

结语

在这篇BLOG中，我们一同学习了KM算法的运算原理和具体程序，赶快去做题练习一下吧！希望你喜欢这篇BLOG！