在众多的线段树题目中，有一种题目一直占有一席之地，那就是染色问题，这篇BLOG，我们就针对染色问题，来浅谈一下这一类问题的解决方法

一维染色问题

这一类题目，一般都有一个固定的样式，当你对题目进行简化以后，总会得到类似与下面这种模型类似：

在一条数轴上，依次进行n次操作，每次操作读入3个数,x,y,z，表示在区间[x,y]中涂上颜色z，后涂上的颜色会覆盖之前涂上的颜色。问最后我们还能看到几种颜色，是哪几种，所覆盖的长度分别为多少？(1≤x≤y≤1e5，n≤1e5）

对于这种题目，初次见到这种题目的同学可能会一脸懵逼，毫无头绪。首先我们先观察一下数据范围，嗯，1≤x≤y≤1e5，n≤1e5，普通的暴力算法复杂度达到了O(n^2),是我们所不能接受的，这个时候，我们就可以考虑怎么样用线段树优化掉一维的n变为log n。

我们考虑可以对于从前往后进行染色，每一次染色都当作一次区间修改，每次强行进行区间修改染色，最后将线段树从上向下的pushup一下，把标记全部下传到根节点就好了。

什么，没怎么听懂，没关系，让我们来举一个例子！

假如我们初始的空白线段长度为8，我们先新开一棵线段树：

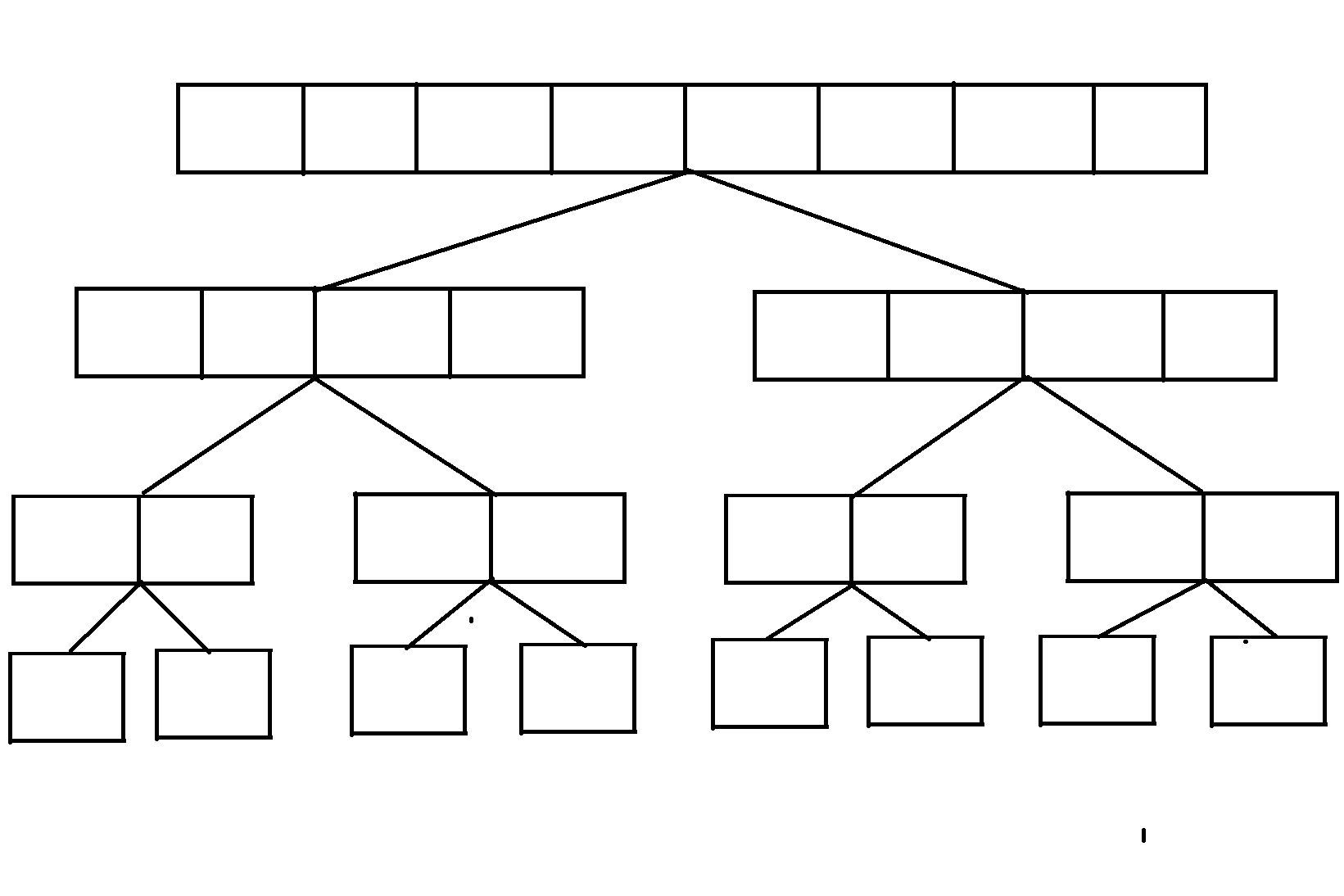
第一次操作，我们把[3,5]染成红色，按照区间修改的思路，把完全覆盖的区间改为红色，并且打上lazy标记：

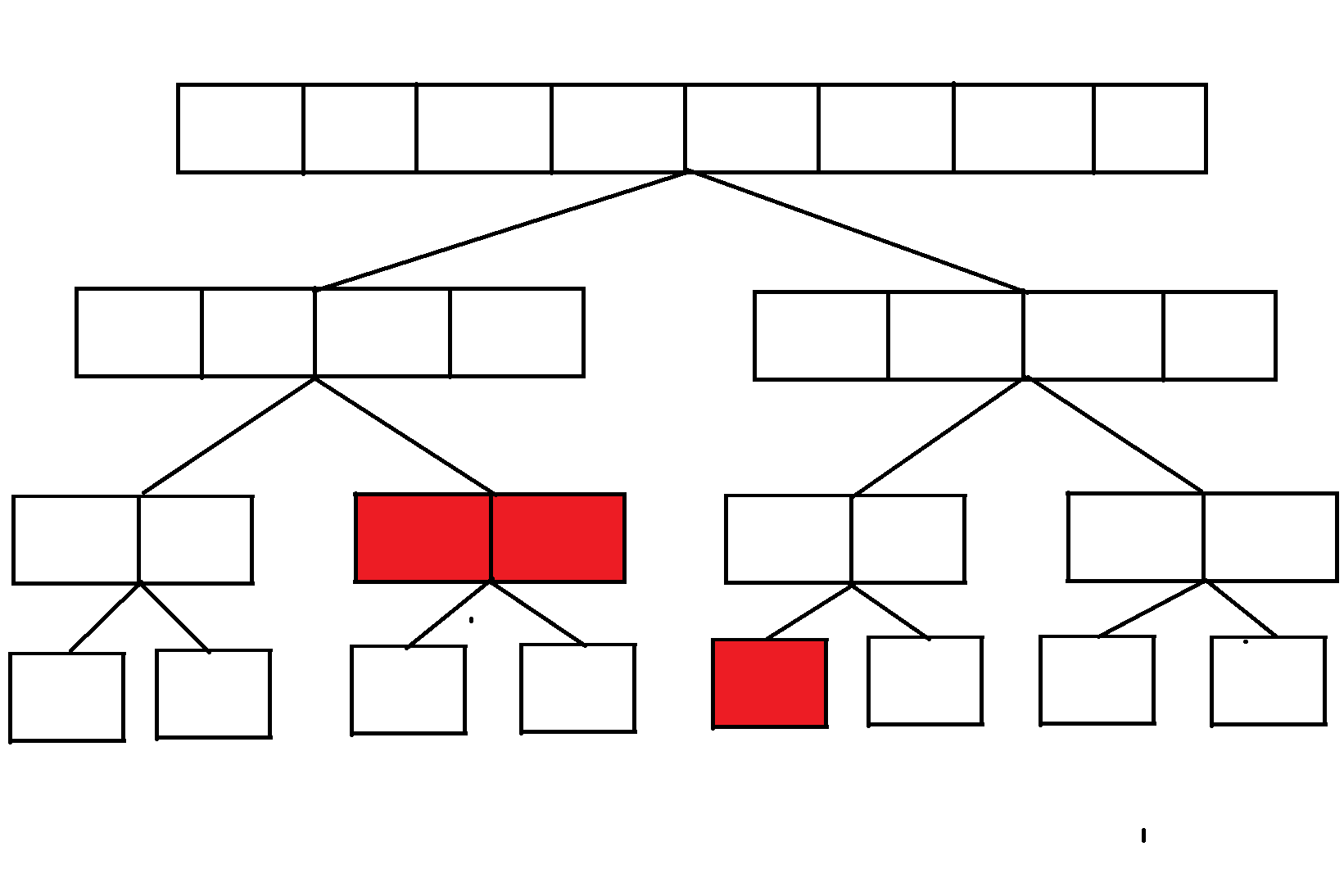
第二次操作，我们把[5,8]染成绿色，按照区间修改的思路，把完全覆盖的区间改为绿色，并且打上lazy标记：

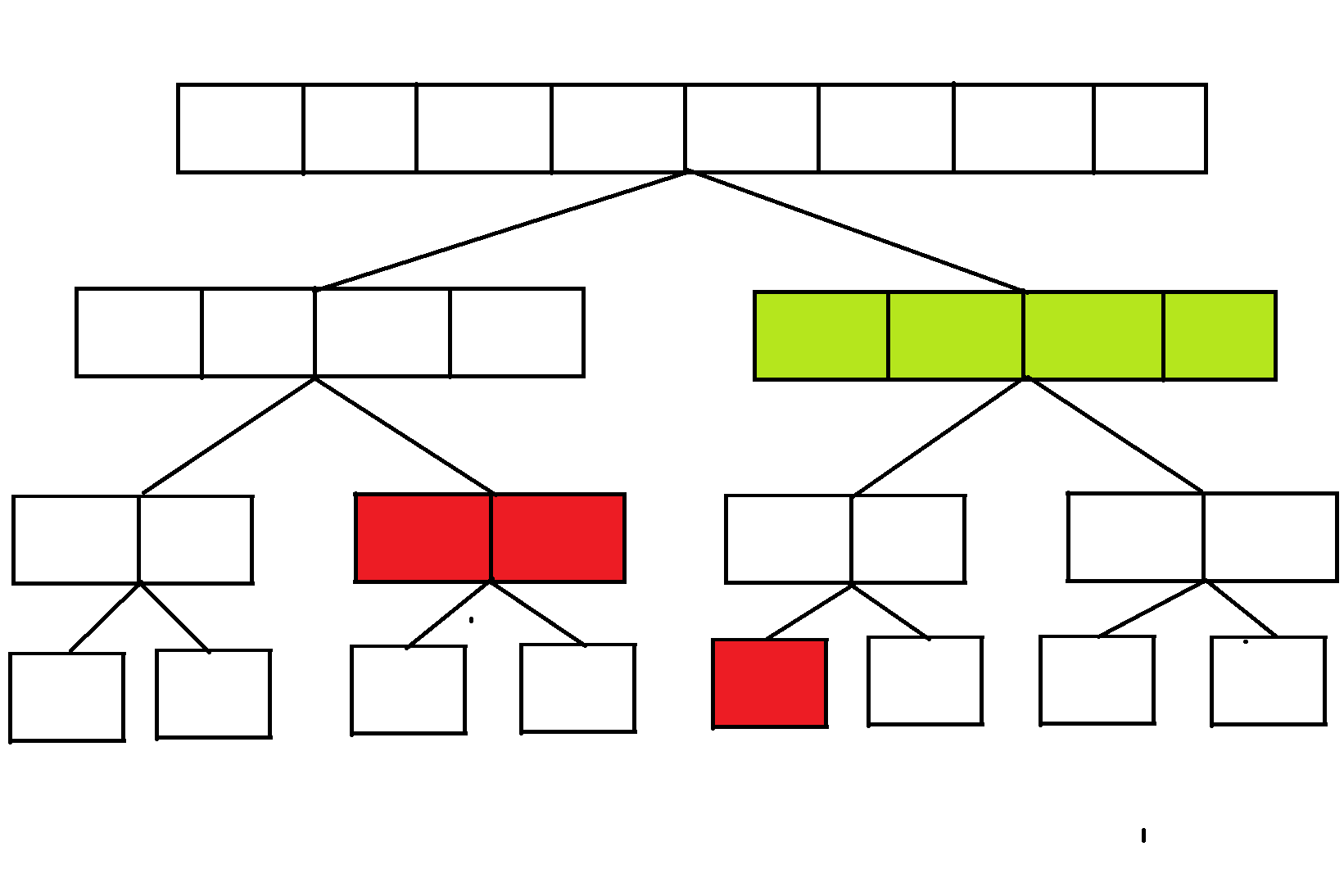
第三次操作，我们把[8,8]染成黄色，在经过绿色标记是时，我们有标记的点下传后再进行操作，按照区间修改的思路，把完全覆盖的区间改为黄色，并且打上lazy标记：

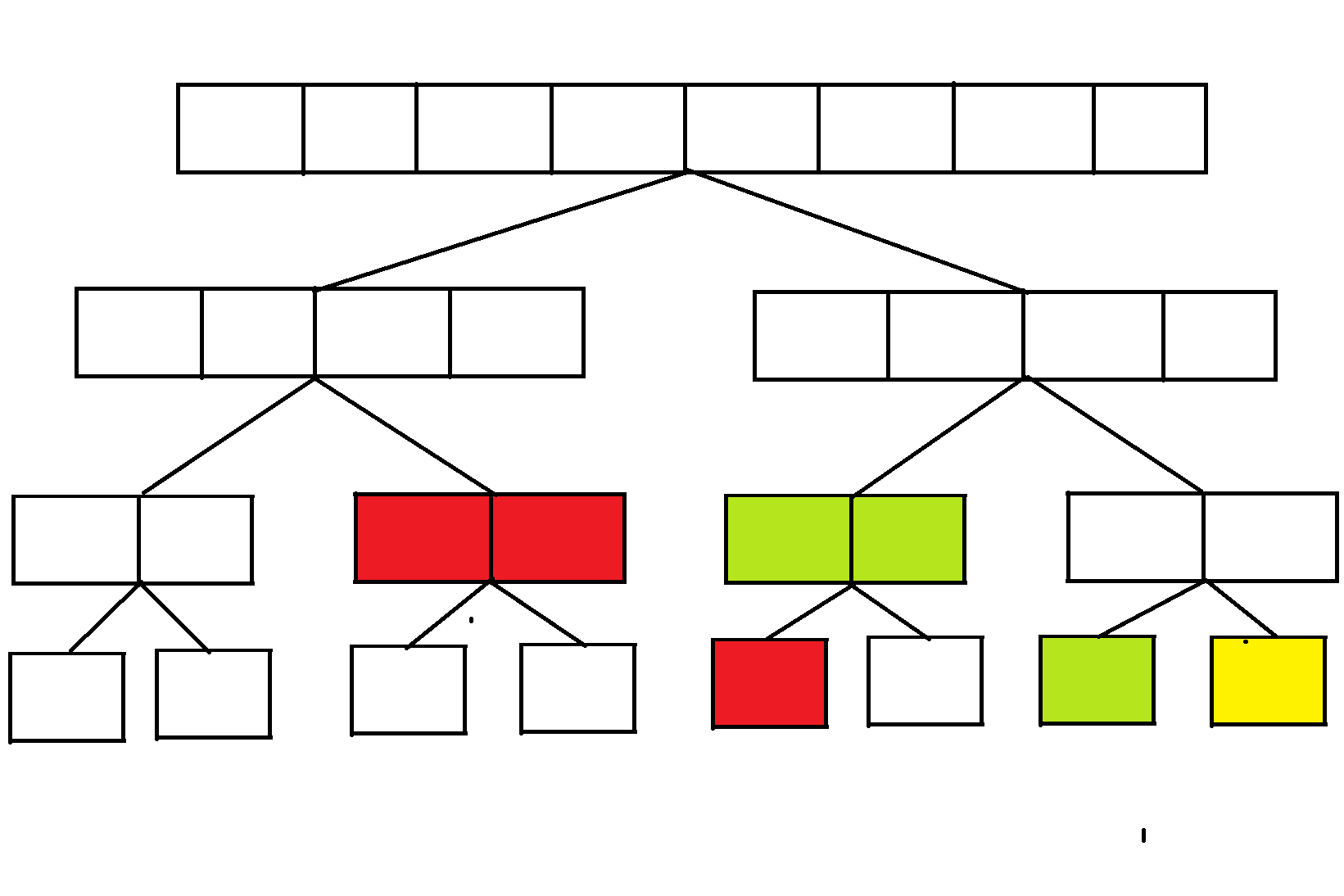
最后一次操作，把[1,4]染成紫色，按照区间修改的思路，把完全覆盖的区间改为紫色，并且打上lazy标记：

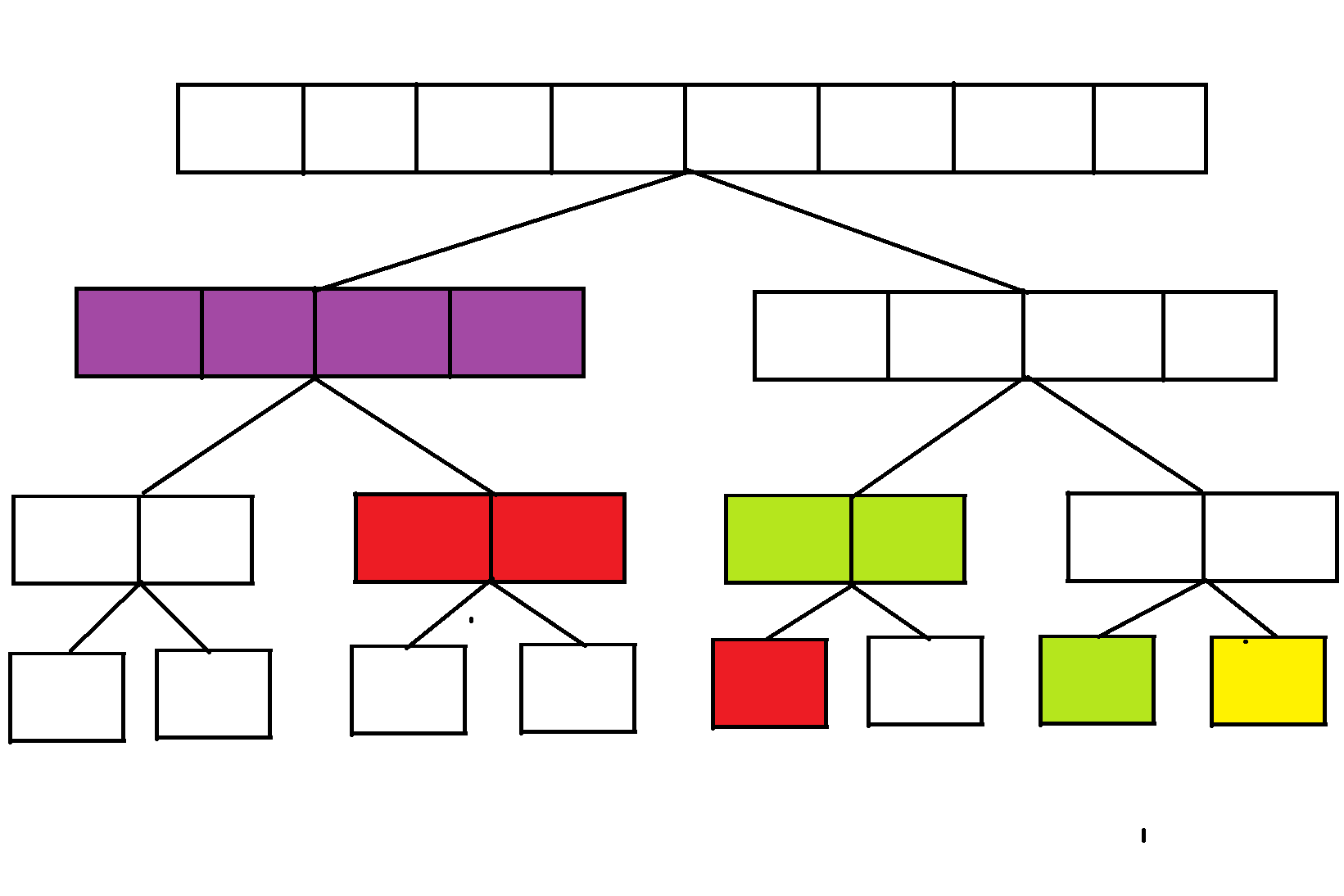
在操纵完成后，我们自上而下把标记全部下传到叶子节点就是最后序列的样子了：

这样一想，是不是很简单啊。

二维染色问题

我们刚刚讨论完一维的染色问题，现在我们来讨论一下二维的染色问题，这类问题和一维染色问题类似，对问题进行简化之后，大概可以变成下面这种样式的模型：

在一个平面上，依次进行n次操作，每次操作读入5个数,x1,y1,x2，y2，z，表示在以[x1,y1]为左下角，[x2,y2]为右上角的矩形中涂上颜色z，后涂上的颜色会覆盖之前涂上的颜色。问最后我们还能看到几种颜色，是哪几种，所覆盖的面积分别为多少？(1≤x1≤x2≤1e5，1≤y1≤y2≤1e5，n≤1e3）

我们再来看一下这道题，其实就是上一题的升级版，我们把上次每次染色都是一维的一条线变成了二维的一个平面。那么我们又要如何维护这个操作呢？首先先考虑最基本的暴力，掐指一算，不论是空间还是时间貌似都是我们无法接受的大小。

很显然地，我们能够想到类似于扫描线算法的一种解法。我们先对每一个矩形的两条纵边进行离散化，由于最多自有1000个矩形，所以最多只能又2000条纵边：

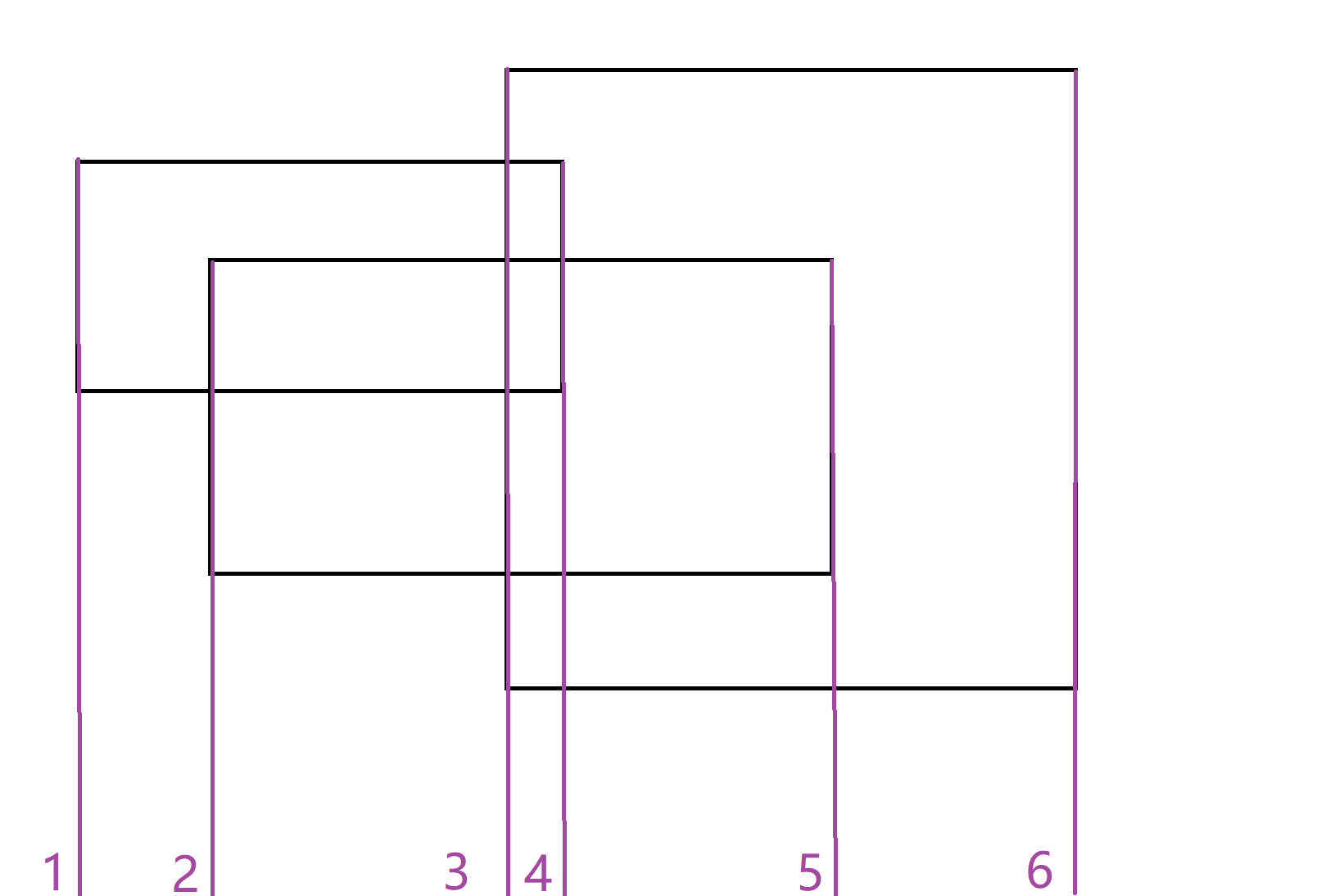
所以你是不是突然有了大胆的想法，为什么不在对横坐标离散化后的相邻两条纵边构成的区间都开一颗线段树呢？对纵坐标再离散化过后，就转化成了第一题的一维区间染色问题。比如我们要对左上角的矩形进行染色，就要对红色标记的1，2，3号线段树进行一维的区间染色。

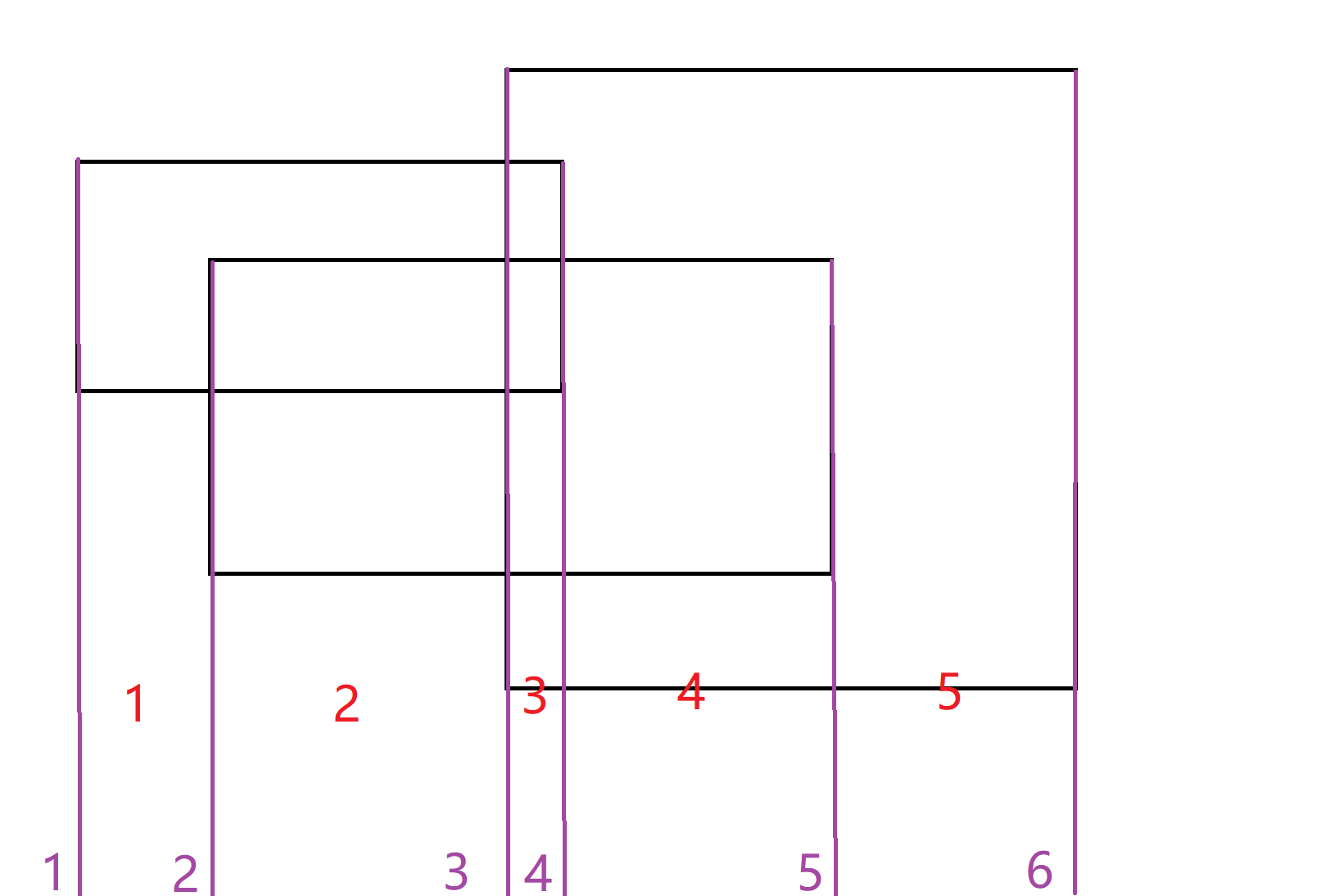
这样操作完成后，最后对于每一棵线段树，都将标记下传到底部叶子节点，最后进行统计就好了。我们最后分析一下它的时间复杂度和空间复杂度。对于每一个矩形，要进行至多2000也就是2n棵线段树的操作，每一次区间染色时间复杂度为O(log n),所以总的时间复杂度为O(n log n),对于空间，最多2000棵线段树，每棵线段树叶子节点最夺2000个节点，若采用堆存储，则共需要4095个节点，每个节点仅仅保存标记值，所以共要保存200040951=8190000个节点才不到32MB，时能够接受的。

所以这种算法时可行且高效的。

三维染色问题

有了二维染色，我们不妨考虑一下三维染色问题。

在一个三维空间上，依次进行n次操作，每次操作读入7个数,x1,y1,z1，x2，y2，z2，o，表示在以[x1,y1,z1]为左下角，[x2,y2,z2]为右上角的立方体内部全部中涂上颜色o，后涂上的颜色会覆盖之前涂上的颜色。问最后空间内还有几种颜色，是哪几种，所覆盖的体积分别为多少？(1≤x1≤x2≤1e5，1≤y1≤y2≤1e5，n≤1e3）

这又是对上一题的一个升级，在一个空间内进行染色。很明显，我们可以先将这个问题放到一个空间直角坐标系里，我们可以先把x轴方向的边离散化，这样在一个立方体中的染色问题，就转化为了多个上题中对平面的染色问题。

接着只要对每个平面都像上一题一样，对沿着y轴方向的再离散化，每个相邻离散边都开一颗线段树就好了。
至于有没有更加优秀的算法，我是暂时没想到，想到的同学可以在底部评论中告诉我你的想法。

结语

通过这篇BLOG，希望大家了解并熟悉类比推理的思想，在你以后的学习生活中能够灵活地运用。希望你喜欢这篇BLOG！