今天在某神犇老师的带领下学习了后缀自动机,刚开始学的时候还是一脸懵逼的,后面在周围大佬们孜孜不倦的帮助下终于学会了后缀数组。这篇BLOG,就让我们携手走进后缀数组吧。
什么是后缀数组
我们先来一个一个概念搞懂:
子串
若我们有一个长度为n的字符串S,设字符串内的点为[1,n],那么我们从中任意截取一段[l,r], 若1≤l≤r≤n,那么称 截取出来的这段子字符串SS为原字符串的子串。即若SS⊆S,则称SS为S的子串。
后缀
那么什么是后缀呢,后缀就是从字符串的某个位置i一直到字符串末尾所构成的的子串,我们定义以S的第i个字符为第一个元素的后缀为 suff(i)。
后缀数组
后缀数组又是干什么的呢?
我们先把S的每个后缀按照字典序排序;
后缀数组sa[i]就表示排名为i的后缀的起始位置的下标;
而它的映射数组rk[i]就表示起始位置的下标为i的后缀的排名;
简单来说,sa[i]表示排名为i的是谁,rk[i]表示第i个的排名是多少;
下面我们来讲讲如何快速求解sa[]数组。
后缀数组的思路
首先我们先引入一个简单的问题:
给你一个字符串s,求第i个字符在整个字符串中的排名(允许排名相同),比如输入 c d a b a,则这五个字符对应的排名分别是 3 4 1 2 1。
是不是非常简单啊,只要统计对于每一种字符有多少种比他排的前的字符(ascⅡ码比它小)出现了,再加一就是答案了。
比如对于a,没有字符排在它的前面,所以对于a的排名就是0+1=1;对于b,只有a排在它的前面,所以它的排名就是1+1=2;对于c,只有a,b排在它的前面,所以它的排名为2+1=3,对于d,出现了a,b,c,所以它的排名为3+1=4。总的时间复杂度为O(n)。
是不是非常简单啊。
我们对问题进行一下升级:
给你一个字符串s,求第i个字符在整个字符串中的排名(不允许排名相同,若字符相同,则在字符串靠前的字符排名更小),比如输入 c d a b a,则这五个字符对应的排名分别是 4 5 1 3 2。
我们考虑一下,我们可以先用O(n)从前往后对整个数组进行扫描,求出每个字符出现了多少次,那么我们就找到了对于每种字符的最大排名为多少。
比如对于字符串 a b a b a c c,一共出现了3个a,2个b,2个c,那么对于字符a,就算你排的再后,排名也会小于等于3;对于字符b,就算你排的再后,排名也会小于等于3+2=5;同理对于字符c,就算你排的再后,排名也会小于等于3+2+2=7。
看到这里你想到了什么?对!前缀和,我们先用前缀和维护每一种字符的排名最多到哪里,第i种字符的排名最大值存储到c[i]里面。那么接下来如何操作呢?
我们很容易可以想到,可以通过反向的一次O(n)向前遍历,由于当字符相同时,越靠后的排名越后,则第i个字符在向前遍历的过程中第一次出现则该点排名为c[i],我们把c[i]--,在下一次再遇到这个点时,一样的,排名仍然为c[i],我们再把c[i]--……听的不是很懂?没事我们举一个栗子:
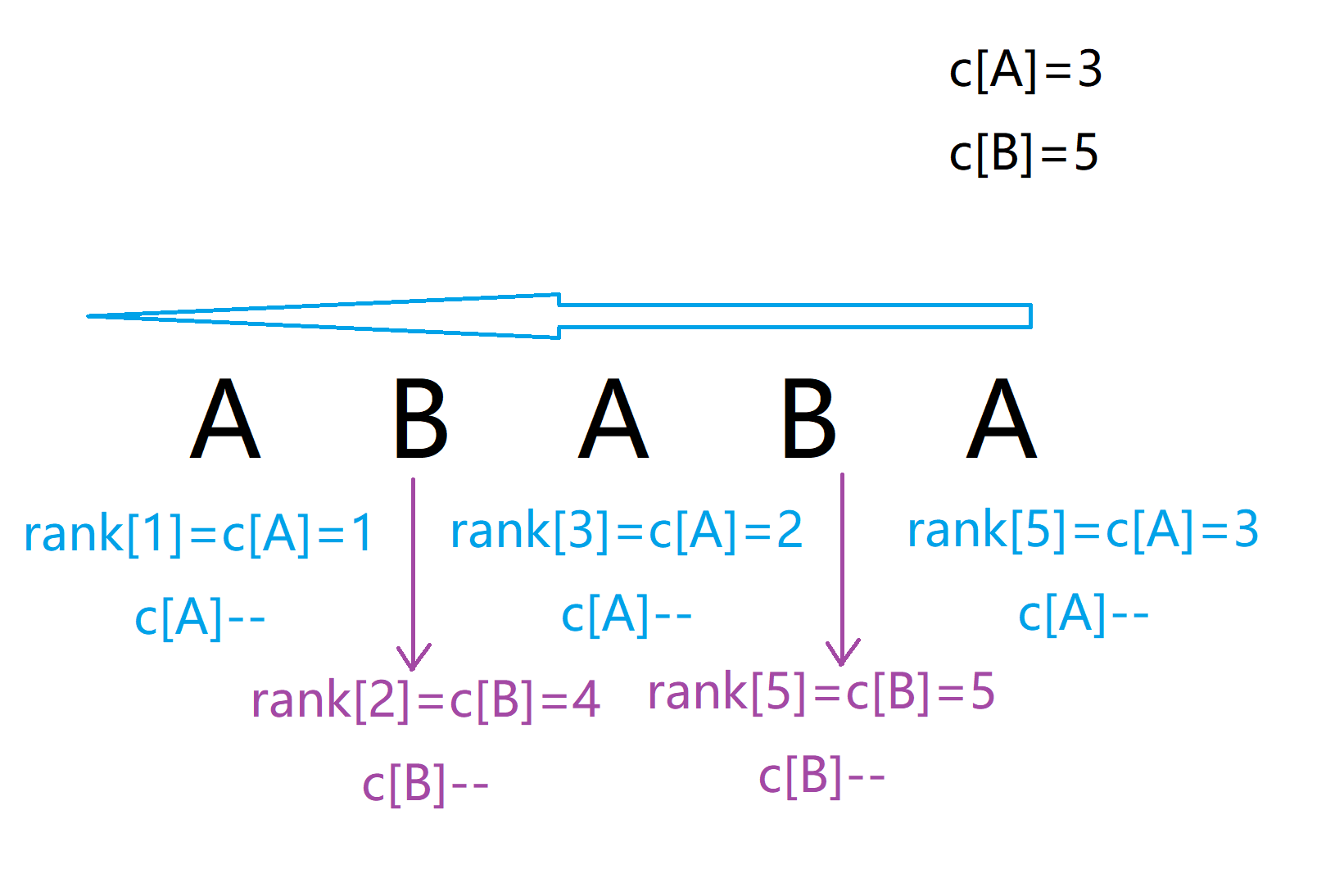
这样我们就可以求出每个字符的排名了。
再对问题升级一下:
给你一个字符串s,求第i个字符和第i+1个字符构成的子串在所有长度为2的子串的排名(1≤i≤n-1),若长度不够则用空格补齐。比如输入 c d a b a,则这五个子串对应的排名分别是 4 5 2 3 1。
这里很明显我们可以先用上一题的方法求出来每个字符在原字符串中的排名,那么题目就变成了一个双关键字的一个排序。比如我们有字符串 A C B A C B D A:
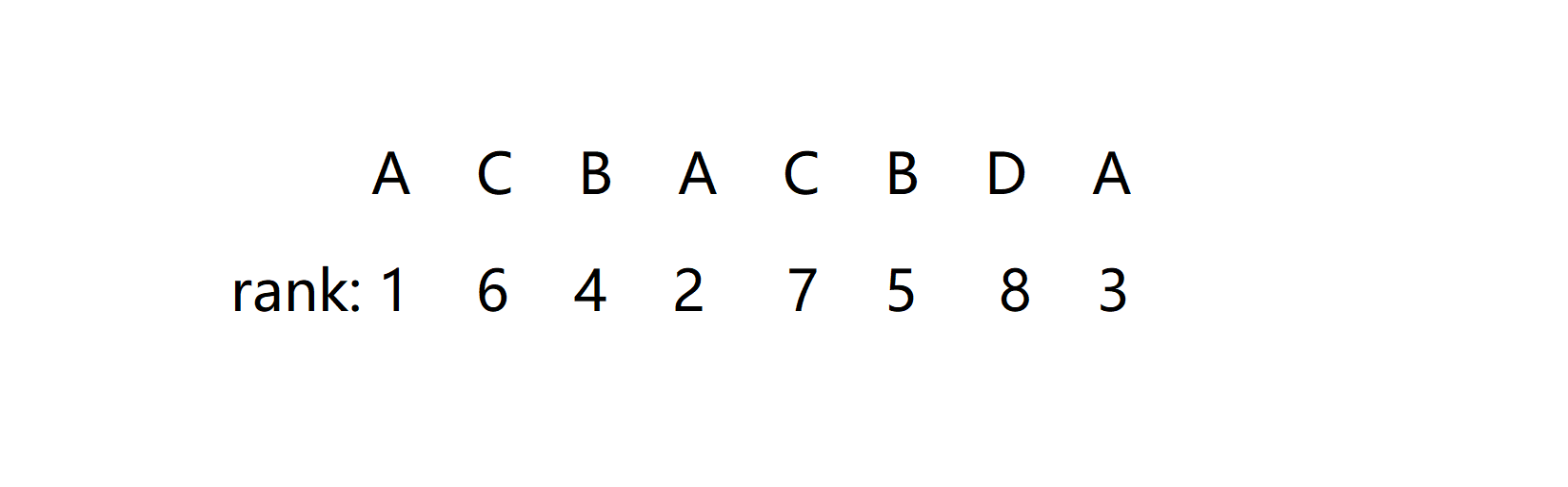
在求出每一个字符的排名后,接下来我们再把相邻的两个关键字合并到一起,就相当于根据每一个后缀的前两个字符进行排序。想想看,这样就是以第一个字符(也就是自己本身)的排名为第一关键字,以第二个字符的排名为第二关键字,把组成的新数排完序之后再次标号。没有第二关键字的补零,接下来对其进行基数排序。
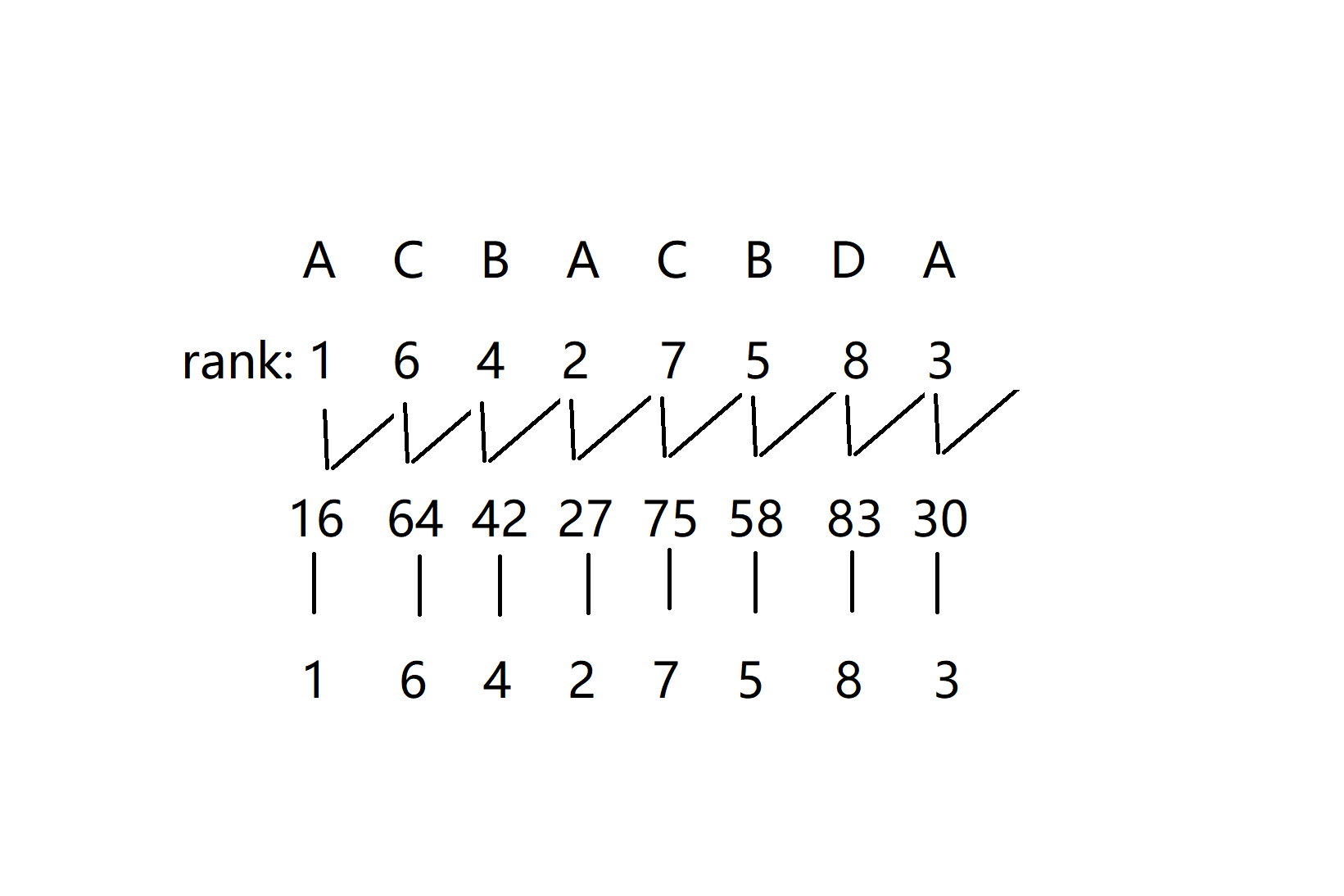
那么什么是基数排序呢?
如果我们用快排的话,复杂度就是(n log^2 n) 还是太大,会TLE的。
所以这里我们用一波基数排序进行排序。在这里我们可以注意到,每一次排序都是排两位数,所以基数排序可以将它优化到O(n)级别,总复杂度就是(n log n)。
介绍一下什么是基数排序,这里就拿两位数举例
我们要建两个桶,一个装个位,一个装十位,我们先把数加到个位桶里面,再加到十位桶里面,这样就能保证对于每个十位桶,桶内的顺序肯定是按个位升序的,自己画一画是可以证明的。
这样排序过后,我们就能得到两个字符组成的子串的排名了。
问题继续升级:
给你一个字符串s,求第i个字符到第i+3个字符构成的子串在所有长度为4的子串的排名(1≤i≤n-1),若长度不够则用空格补齐。比如输入 c d a b a,则这五个子串对应的排名分别是 4 5 2 3 1。
首先这道题和上一道题目的区别就在于,上面一题要排序的子串长度为2,而这一题为4。类比上一题,上面一题我们是对相邻的两个字符,也就是长度为1的子串进行基数排序,所以这一道题我们也可以在上一题的基础上,对相邻的两个长度为2的两个子串进行基数排序就可以得出答案了!我们通过对上一题的分析,发现这两道题的本质是一样的,都是对于两个相邻的两个块组合,进行基数排序得到答案。
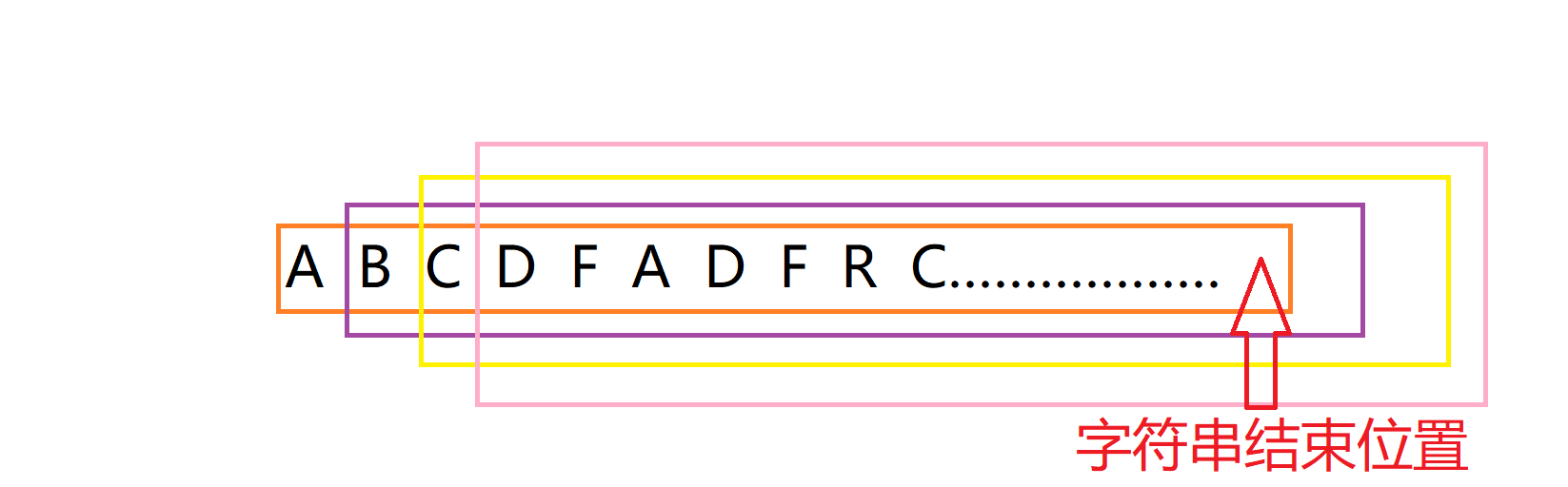
不如推广一下:
按照上面这样,对子串长度为1,2,4……2^k(2^k≥n)进行倍增求解,就可以得出长度为2^k(2^k≥n)的子串长度,又由于现在子串长度已经大于等于原序列长度了,又由于不足的位置都是补空,所以求解出来的也就是后缀的排名了。
实现后缀数组
那么我们要如何用程序实现以第i的字符开头的后缀的排名,也就是sa[i]呢?在上面的思路当中我们已经讲的很详细了,下面我们就直接来看程序实现:
在只求解sa[]的题目中,我们只要记住下面的模板:
【感谢 victorique 大佬的板子,我另外加入了一些注解方便大家理解】
void get_sa()
{
//s为读入的字符串,n为字符串长度,m为s中每个关键字的大小(初始为s数组内的最大值)
for(int i=1;i<=n;i++)c[x[i]=s[i]]++;
//c数组是桶
//x[i]是第i个元素的第一关键字
for(int i=2;i<=m;i++)c[i]+=c[i-1];
//做c的前缀和,我们就可以得出每个关键字最多是在第几名
for(int i=n;i>=1;i--)sa[c[x[i]]--]=i;
for(int k=1;k<=n;k=k*2)
{
num=0;
for(int i=n-k+1;i<=n;i++)y[++num]=i;
//y[i]表示第二关键字排名为i的数,第一关键字的位置
//第n-k+1到第n位是没有第二关键字的 所以排名在最前面
//又由于当第一关键字在n-k+1到第n位时都是不完整的,所以第一关键字的排名一定不一样
//所以此时这些点的第二关键字谁先谁后都无所谓了
//也就是说 for(int i=n;i>=n-k+1;i--)y[++num]=i;也是对的
for(int i=1;i<=n;i++)if(sa[i]>k)y[++num]=sa[i]-k;
//排名为i的数 在数组中是否在第k位以后
//如果满足(sa[i]>k) 那么它可以作为别人的第二关键字,就把它的第一关键字的位置添加进y就行了
//所以i枚举的是第二关键字的排名,第二关键字靠前的先入队
for(int i=1;i<=m;i++)c[i]=0;
//初始化c桶
for(int i=1;i<=n;i++)c[x[i]]++;
//因为上一次循环已经算出了这次的第一关键字 所以直接加就行了
for(int i=2;i<=m;i++)c[i]+=c[i-1];//第一关键字排名为1~i的数有多少个
for(int i=n;i>=1;i--)sa[c[x[y[i]]]--]=y[i],y[i]=0;
//因为y的顺序是按照第二关键字的顺序来排的
//第二关键字靠后的,在同一个第一关键字桶中排名越靠后
//基数排序
swap(x,y);
//这里不用想太多,因为要生成新的x时要用到旧的,就把旧的复制下来,没别的意思
x[sa[1]]=1;num=1;
for(int i=2;i<=n;i++)
if(y[sa[i]]==y[sa[i-1]] && y[sa[i]+k]==y[sa[i-1]+k])x[sa[i]]=num;
else x[sa[i]]=++num;
//因为sa[i]已经排好序了,所以可以按排名枚举,生成下一次的第一关键字
if(num==n)break;
//如果num==n表示各个后缀的先后顺序已经分出来了,直接输出就好了
m=num;
//这里就不用最开始的m了,因为都有新的编号了
}
}神奇的height数组
当你学完上面的后缀数组,兴高采烈地去做题时,你会一脸懵逼地发现,怎么这么多题目不知道怎么做啊,因为你还没有学会如何构造height数组。
经典模型
给你一个长度为n的字符串,先将后缀进行排名,然后求解排名相邻的后缀之间的最长公共前缀时多少?
我们先来举一个例子,我们有一个字符串 ABABA,那么后缀的排名和相邻两个的前缀就是:
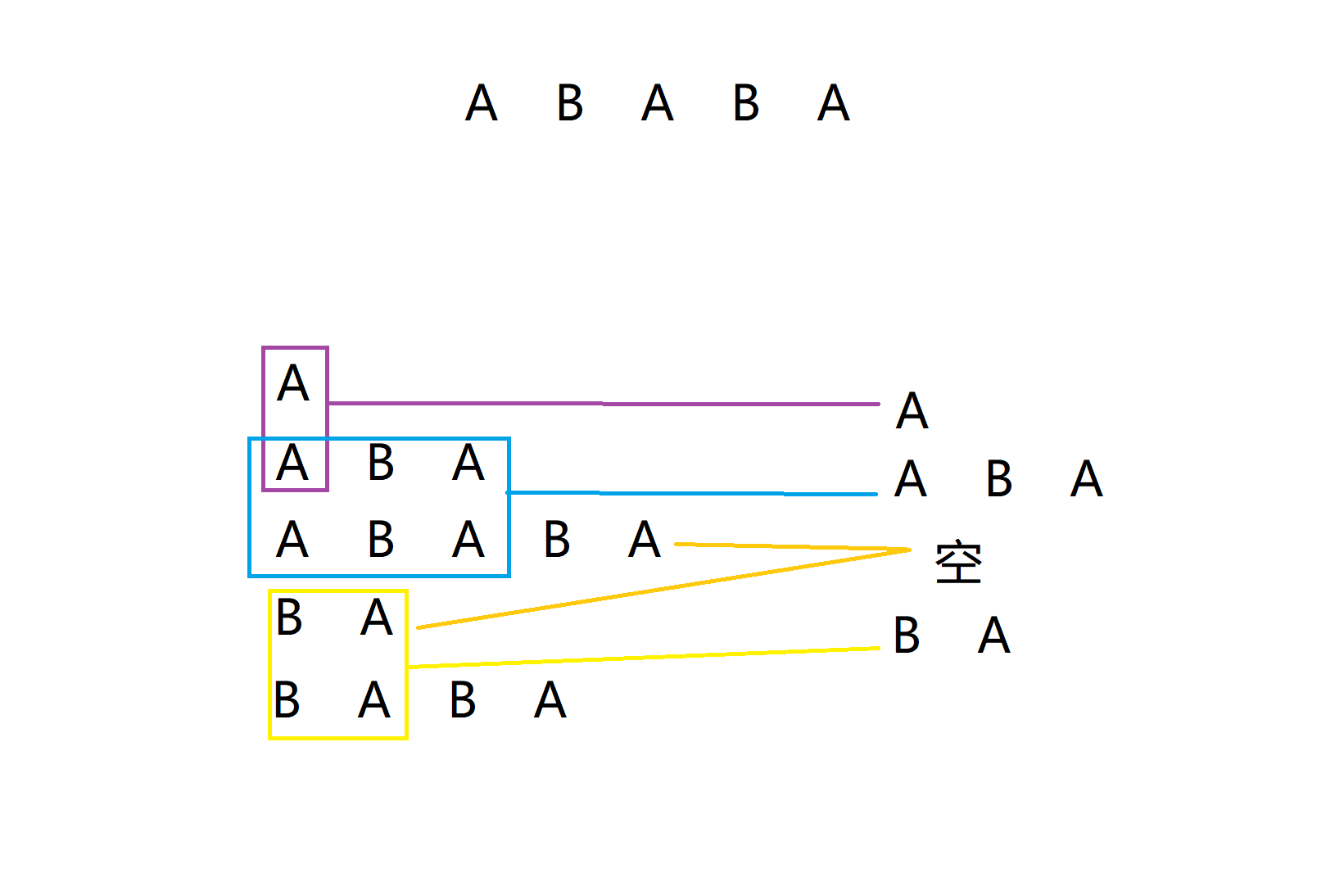
那么我们要如何求解呢,考虑最暴力的算法,对于每两个相邻的后缀都暴力地算一下公共前缀为多长,这样的复杂度达到了O(n^2),肯定会超时的。
我们考虑一下能不能利用一下之前存储过的信息来达到O(n),答案时肯定的,我们假如有一个串 ABCDEFGABCD:我们对于第一个字符的后缀ABCDEFGABCD,前一个为ABCD,最长的公共前缀为ABCD,那么在第二个字符开头的后缀BCDEFGABCD,前一个至少也一定时上面那个串后移也就是BCD,同理C和D的也能轻松求出。
那么这个时为什么呢?考虑一下,如果BCDEFGABCD的前一个不是BCD时,那前一个一定有一个前缀BCD,后面是什么不重要了。此时最长公共前缀也至少是BCD了。
此时也只要开一个类似双指针的结构就可以了。
程序实现
void get_height()
{
int k=0;
for(int i=1;i<=n;i++)rank[sa[i]]=i;
for(int i=1;i<=n;i++)
{
if(rank[i]==1)continue;//第一名height为0
if(k>0)k--;//h[i]>=h[i-1]+1;
int j=sa[rank[i]-1];
while(i+k<=n && j+k<=n && s[i+k]==s[j+k])k++;
height[rank[i]]=k;//h[i]=height[rk[i]];
}
}经典例题
这次就不拿裸题了,我们直接上省选原题!
[BZOJ 1031] JSOI2007字符加密Cipher
Description
喜欢钻研问题的JS同学,最近又迷上了对加密方法的思考。一天,他突然想出了一种他认为是终极的加密办法
:把需要加密的信息排成一圈,显然,它们有很多种不同的读法。例如下图,可以读作:JSOI07 SOI07J OI07JS I07JSO 07JSOI 7JSOI0把它们按照字符串的大小排序:07JSOI 7JSOI0 I07JSO JSOI07
OI07JS SOI07J读出最后一列字符:I0O7SJ,就是加密后的字符串(其实这个加密手段实在很容易破解,鉴于这是
突然想出来的,那就^^)。但是,如果想加密的字符串实在太长,你能写一个程序完成这个任务吗?
Input
输入文件包含一行,欲加密的字符串。注意字符串的内容不一定是字母、数字,也可以是符号等。Output
输出一行,为加密后的字符串。Sample Input
JSOI07
Sample Output
I0O7SJ
HINT
对于100%的数据字符串的长度不超过100000。
考虑一下这道题怎么做,既然是一个环,那么我们很容易想到先把字符串double一下然后接到原字符串后面。首先我们设原字符长度为n,那么double后字符长度变为n*2,然后我们跑一遍后缀数组,排名从小到大进行操作,如果当前排名的后缀开头出现在前n的字符里的为由校长,只要输出这个开头往后n-1个字符就好了,附上代码,也是后缀数组的模板。
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
char s[1100000];
int x[1100000],y[1100000],c[1100000],sa[1100000],rank[1100000],height[1100000];
int i,j,m,n,o,p,js,jl,num;
void get_sa()
{
//s为读入的字符串,n为字符串长度,m为s中每个关键字的大小(初始为s数组内的最大值)
for(int i=1;i<=n;i++)c[x[i]=s[i]]++;
//c数组是桶
//x[i]是第i个元素的第一关键字
for(int i=2;i<=m;i++)c[i]+=c[i-1];
//做c的前缀和,我们就可以得出每个关键字最多是在第几名
for(int i=n;i>=1;i--)sa[c[x[i]]--]=i;
for(int k=1;k<=n;k=k*2)
{
num=0;
for(int i=n-k+1;i<=n;i++)y[++num]=i;
//y[i]表示第二关键字排名为i的数,第一关键字的位置
//第n-k+1到第n位是没有第二关键字的 所以排名在最前面
//又由于当第一关键字在n-k+1到第n位时都是不完整的,所以第一关键字的排名一定不一样
//所以此时这些点的第二关键字谁先谁后都无所谓了
//也就是说 for(int i=n;i>=n-k+1;i--)y[++num]=i;也是对的
for(int i=1;i<=n;i++)if(sa[i]>k)y[++num]=sa[i]-k;
//排名为i的数 在数组中是否在第k位以后
//如果满足(sa[i]>k) 那么它可以作为别人的第二关键字,就把它的第一关键字的位置添加进y就行了
//所以i枚举的是第二关键字的排名,第二关键字靠前的先入队
for(int i=1;i<=m;i++)c[i]=0;
//初始化c桶
for(int i=1;i<=n;i++)c[x[i]]++;
//因为上一次循环已经算出了这次的第一关键字 所以直接加就行了
for(int i=2;i<=m;i++)c[i]+=c[i-1];//第一关键字排名为1~i的数有多少个
for(int i=n;i>=1;i--)sa[c[x[y[i]]]--]=y[i],y[i]=0;
//因为y的顺序是按照第二关键字的顺序来排的
//第二关键字靠后的,在同一个第一关键字桶中排名越靠后
//基数排序
swap(x,y);
//这里不用想太多,因为要生成新的x时要用到旧的,就把旧的复制下来,没别的意思
x[sa[1]]=1;num=1;
for(int i=2;i<=n;i++)
if(y[sa[i]]==y[sa[i-1]] && y[sa[i]+k]==y[sa[i-1]+k])x[sa[i]]=num;
else x[sa[i]]=++num;
//因为sa[i]已经排好序了,所以可以按排名枚举,生成下一次的第一关键字
if(num==n)break;
//如果num==n表示各个后缀的先后顺序已经分出来了,直接输出就好了
m=num;
//这里就不用最开始的m了,因为都有新的编号了
}
}
/*
void get_height()
{
int k=0;
for(int i=1;i<=n;i++)rank[sa[i]]=i;
for(int i=1;i<=n;i++)
{
if(rank[i]==1)continue;//第一名height为0
if(k>0)k--;//h[i]>=h[i-1]+1;
int j=sa[rank[i]-1];
while(i+k<=n && j+k<=n && s[i+k]==s[j+k])k++;
height[rank[i]]=k;//h[i]=height[rk[i]];
}
}
*/
int main()
{
scanf("%s",s+1);
n=strlen(s+1);
for(int i=n+1;i<=2*n;i++)s[i]=s[i-n];
n=n*2;
m=256;//由于我们每次读入的字符都在ascⅡ范围内,所以c数组的大小初始只要开到ascⅡ码的上限,也就是256就好啦
get_sa();
for(int i=1;i<=n;i++)if(sa[i]<=n/2)printf("%c",s[sa[i]+n/2-1]);
return 0;
}结语
通过这篇BLOG,我们已经了解了后缀数组的用法和原理,希望你能将它灵活地运用到以后的比赛里。希望你喜欢这篇BLOG!
博主我想问一下,在get_height()里面的第7行的注释是 // h[i]>=h[i-1]+1; 难道不应该是 // h[i] >= h[i-1]-1; 吗
天哪!
博主你的文章质量为什么可以这么高!
这是我唯一一篇看得懂的入门诶
吹爆!
写得太棒啦!
然后再 微微吐槽一下
height和h数组都是什么啊喂(掀桌
果然是偷懒了吧
幸好前面讲的超级清白
再看其它人的博客也没有大问题了
(ฅ´ω`ฅ)
(ฅ´ω`ฅ)
height的程序实现似乎跟其它博主写得不太一样?
int j=sa[rank[i]-1] 感觉好像更对诶
然后还发现一个小小小小小的bug |´・ω・)ノ
"我们对问题进行一下升级"中的例子
实际上有2个c, 而且c的排名一定小于等于7而不是6
(逃
果然是出锅了,是两个c…………我我我蠢了,望原谅,至于 j=sa[rank[i]-1]的问题我再看看[请原谅文化课降智商.....]
文化课加油!
呀酱紫的吗,好尴尬,好像出锅的样子.......我看看去改一下.......谢谢你的提议!!!
哈哈哈,偷懒被发现了[今天才又碰到了电脑的说],真的感谢你喜欢这篇BLOG!!!
∠( ᐛ 」∠)_
对这里是我蠢了……应该是sa[rank[i]-1],已经修复啦,请放心食用!
催更字符串哈希大法
已经收到您的催更,我码完这段时间学的就去复习哈希orz