在我们之前接触到的题目里面，线段树的叶子节点都是保存单点的值，其他节点都是保存一个区间的值，这种题目的一些基本构造想法在浅谈线段树的构造(一)中已经提及到了。但你想过吗，当叶子节点保存一个区间的值时，你该如何构造？

从经典的例题谈起

我们先看一道POI2015的经典例题：

【BZOJ p3747】[POI2015]Kinoman
Time Limit: 60 Sec Memory Limit: 128 MB

Description
共有m部电影，编号为1~m，第i部电影的好看值为w[i]。
在n天之中（从1~n编号）每天会放映一部电影，第i天放映的是第f[i]部。
你可以选择l,r(1<=l<=r<=n)，并观看第l,l+1,…,r天内所有的电影。如果同一部电影你观看多于一次，你会感到无聊，于是无法获得这部电影的好看值。所以你希望最大化观看且仅观看过一次的电影的好看值的总和。
Input
第一行两个整数n,m(1<=m<=n<=1000000)。
第二行包含n个整数f[1],f[2],…,fn。
第三行包含m个整数w[1],w[2],…,wm。
Output
输出观看且仅观看过一次的电影的好看值的总和的最大值。
Sample Input
9 4
2 3 1 1 4 1 2 4 1
5 3 6 6

Sample Output
15

样例解释：
观看第2,3,4,5,6,7天内放映的电影，其中看且仅看过一次的电影的编号为2,3,4。

正常的暴力想法

正常来说，看到这种需要求区间最大独立集的题目，枚举左端点是少不了了，这里就需要一个O(n)的时间复杂度。暴力的来想，我们貌似无法快速确定右端点在哪里，那怎么办？枚举啊！

我们对于每一个枚举的左端点i，都开一个数组f[]，在枚举到的每一个右端点j时，f[]的每一个点f[k]都表示在区间[i,j]中，第k种颜色出现了f[k]次，那么处理方法就很显然了：当我们在枚举右端点j时，每加入一个点o，f[o]++。若此时f[o]==1，就代表之前这部电影都没有放映过，就把这部电影的有趣值加上；若此时f[o]==2，就代表之前这部电影恰好放映过一次，这时就把这部电影的有趣值减去；其他情况不做处理就好了。在加入每一个右端点并处理完后，与最后答案ans比较大小，若比ans大则更新ans为这次处理完的结果。

不要忘了在每次处理完一个左端点的所有右端点的情况后，在开始下一个左端点前，先把f[]数组清空。

想法还是非常暴力的，但是n，m都达到了 1e6的规模，对于我们这种O(n^2)的算法，大数据下是肯定TLE的，那我们就考虑能不能优化掉一维？

叶子节点保存区间信息的线段树

首先我们考虑，对于枚举左节点的一层O(n),是非常难省去的，接下来我们就只能考虑把枚举右节点的一层O(n)替换成开始时O(n log n)的预处理和每对于每一层左节点变化时 O(log n)的修改和查询，总的时间复杂度控制在 O(n log n)，可以卡着时间过。

考虑一下要支持对于左节点枚举时每一层的修改和查询到O(log n)，我们只能考虑用数据结构来维护。说到O(log n)的时间复杂度，我们就要第一时间考虑到树状结构。而树状数组和线段树又是我们最熟悉的能完成修改和区间最值的查询，又由于树状数组和线段树的功能是一致的，我们在这里可以仅仅考虑怎样运用线段树来优化右端点枚举的那一层。

对于我们之前熟知的线段树，每一个叶子节点都只保存单点的值，非叶子节点都保存所包含的底层叶子节点的值的总和。那在这道题中，底层若保存单点的值有什么用呢？合并成一个区间时又要怎么操作呢？考虑一下我们的瓶颈出现在哪里：如果叶子节点仅仅保存这个点的有趣值，那么在区间合并时我们无法判断某几个节点的电影会不会重合，若重合就会导致有趣值变成0，要是能直接知道某一个区间的总和就好了。

那我们这样的话可以换一个思路，如果叶子节点保存的不是某一个单点的值，而是一个区间的值呢？对于我们所枚举到的每一个左端点i，第j个叶子节点代表的是区间[i,j]的电影所获得的有趣值的值，就如下图：

当我们此时左节点为一时，叶子节点1维护的就是【1，1】的电影的有趣值也就是1，叶子节点2维护的就是【1，2】的电影的有趣值也就是1+2=3，叶子节点2维护的就是【1，3】的电影的有趣值：由于1和1重复了，所以只剩下了2……以此类推：

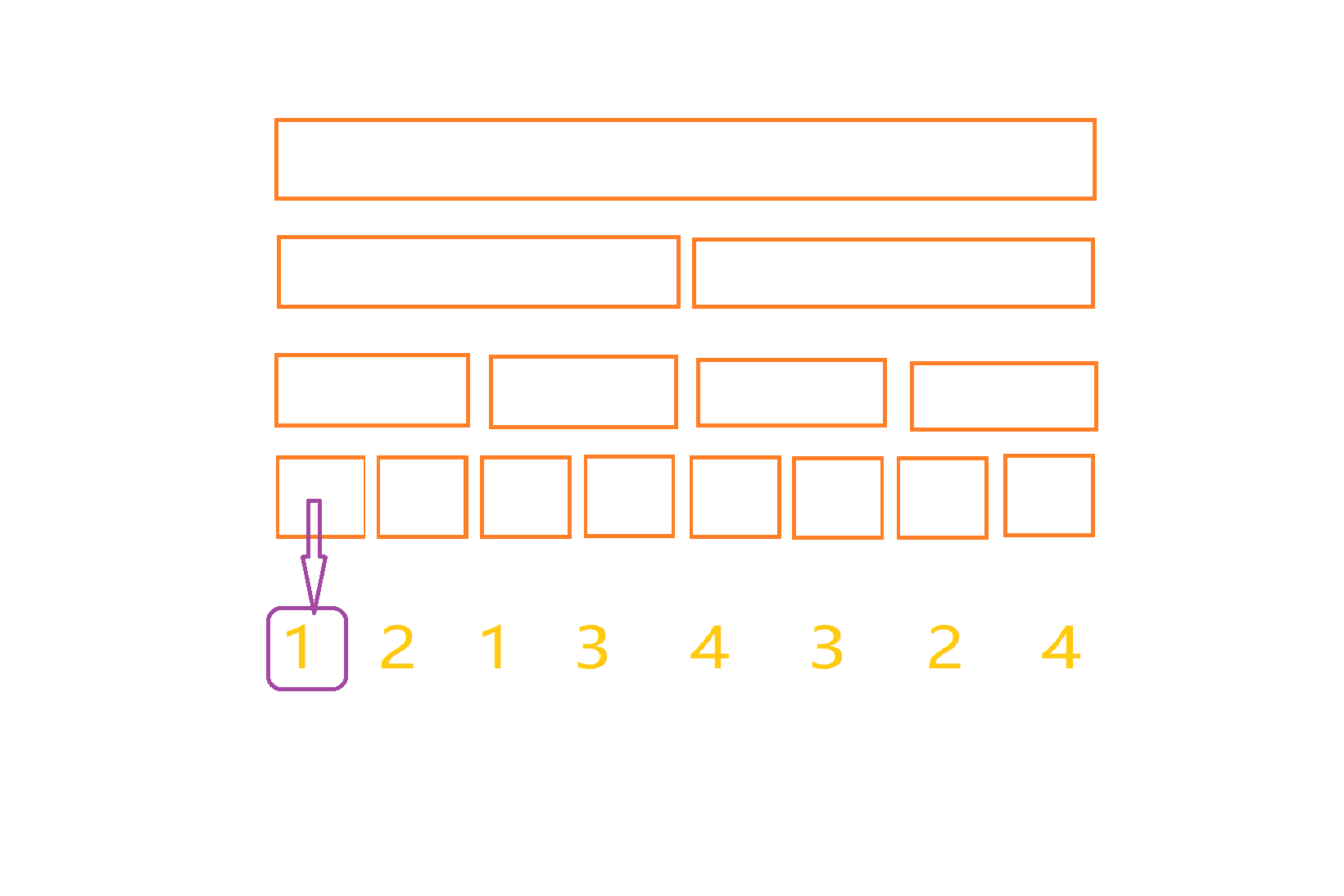
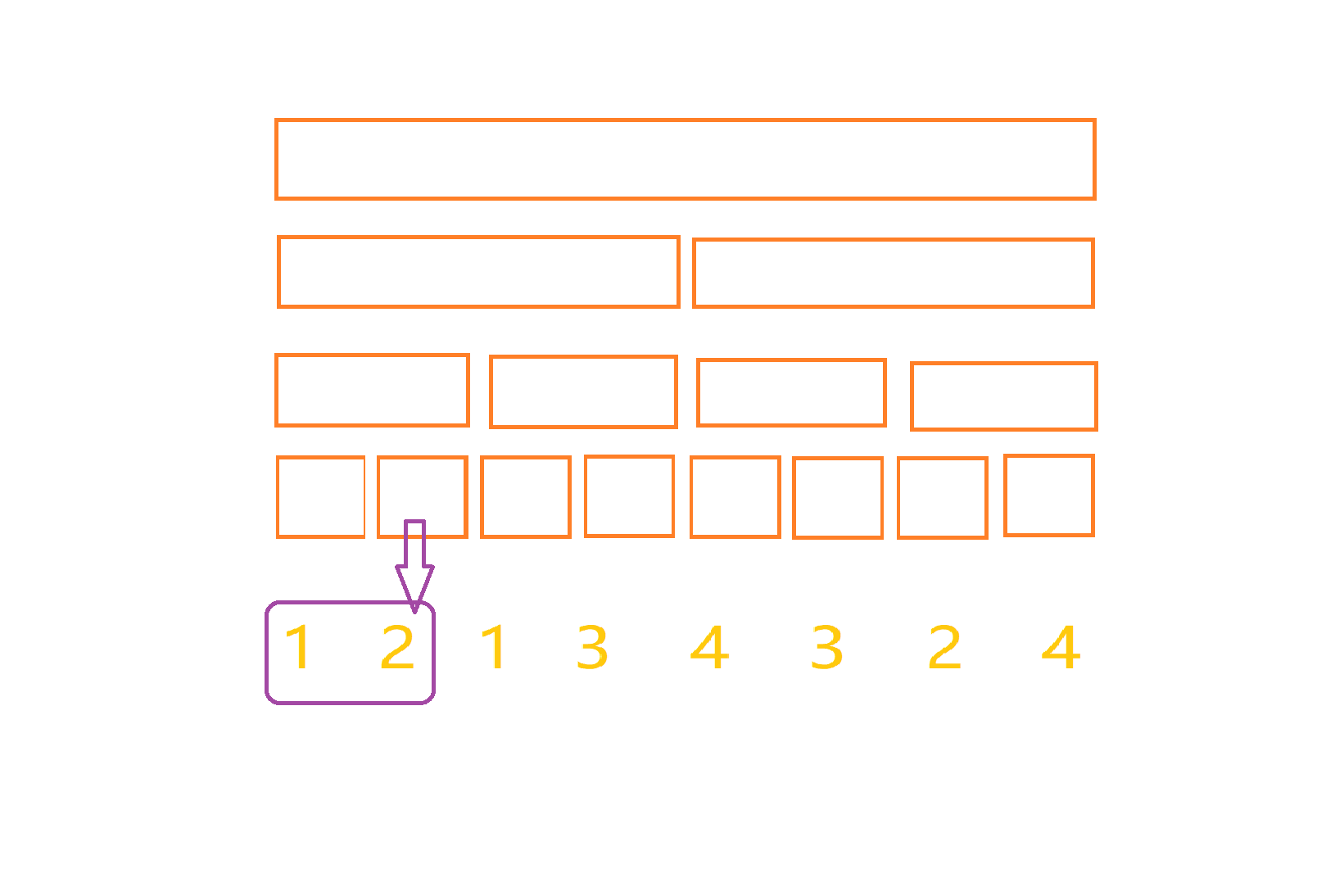
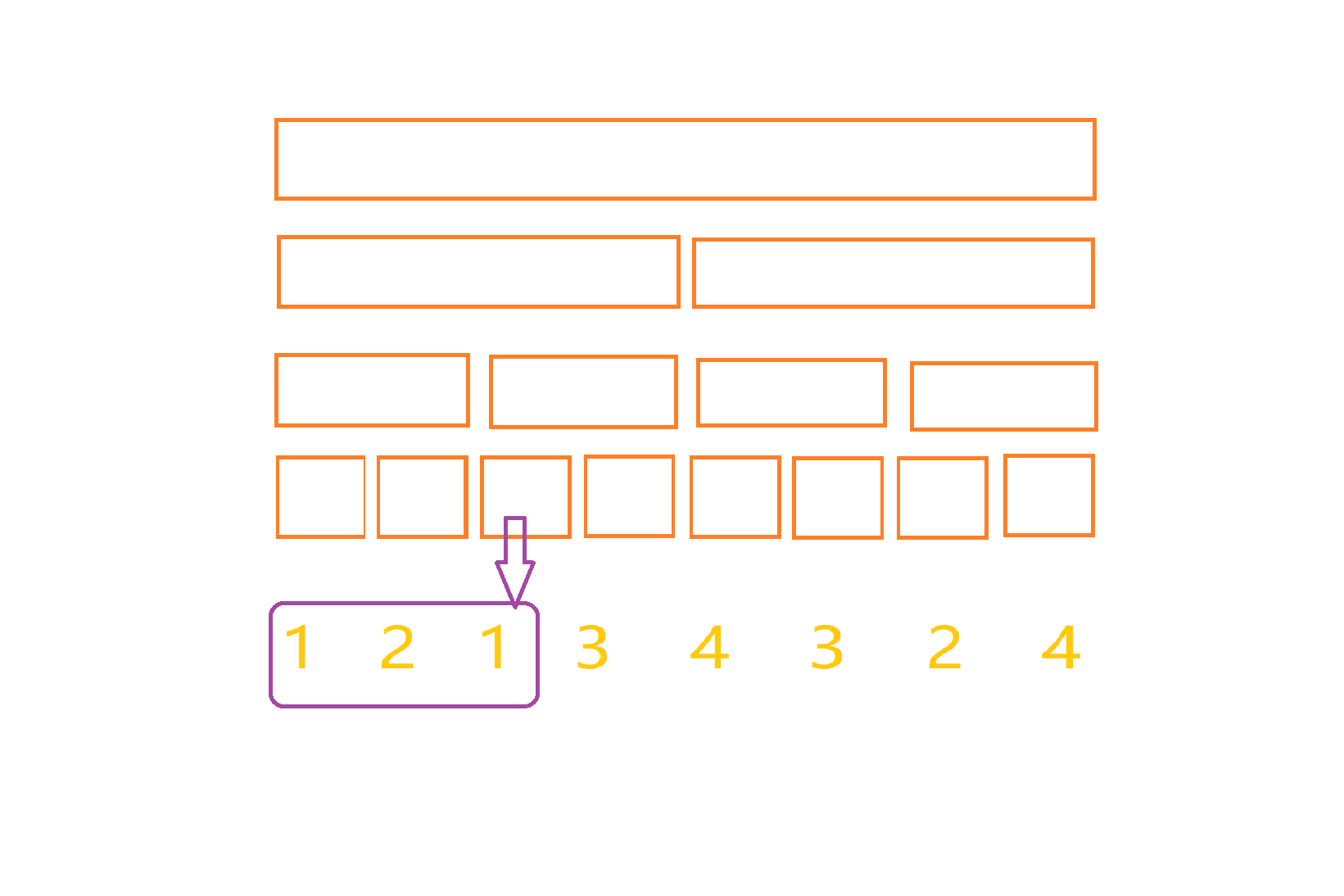
那么对于的每一个非叶子节点都保存其控制的两个子节点节点的最大值就可以了，比如对于上面的栗子，我们处理完底层以后，每一个非叶子节点都等于两个子节点的最大值：

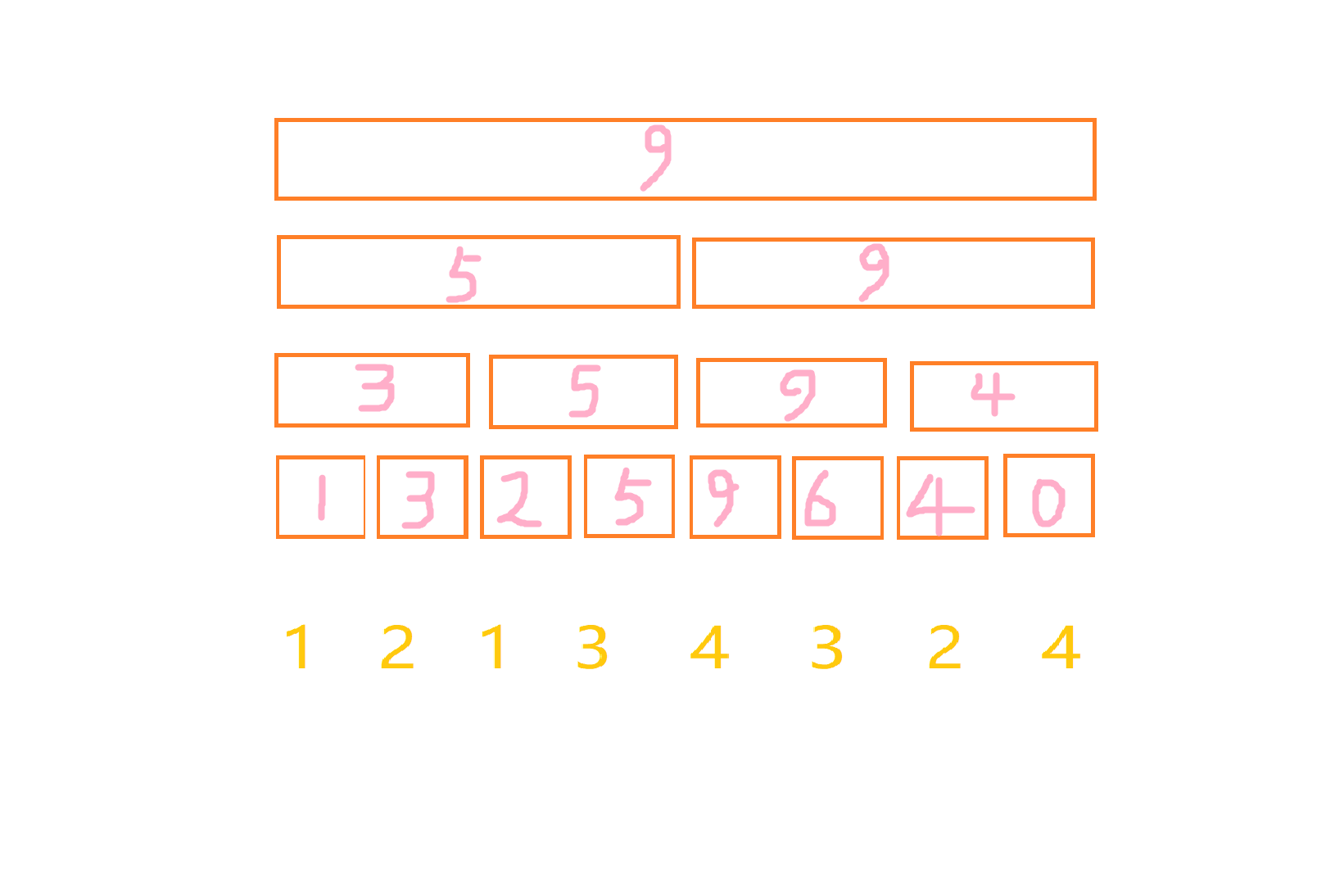
在输出的时候只要输出根节点的max值就好了。

那么操作就迎刃而解了——当我们在预处理时，可以把第1天到任意一天之间的电影的有趣值预处理出来，那么如何预处理呢？考虑对于任意一种电影，若第一次出现的天数是
first[i],我们先预处理出一个next[]数组，next[i]表示下一个和第i天相同的电影出现在第next[i]天，也就是i的后继值，那么我们只要在区间[first[i]，next[first[i]]-1]都加上这部电影的有趣值就好了，比如在上面的栗子当中，我们对于每一个颜色进行考虑，比如对于电影一：

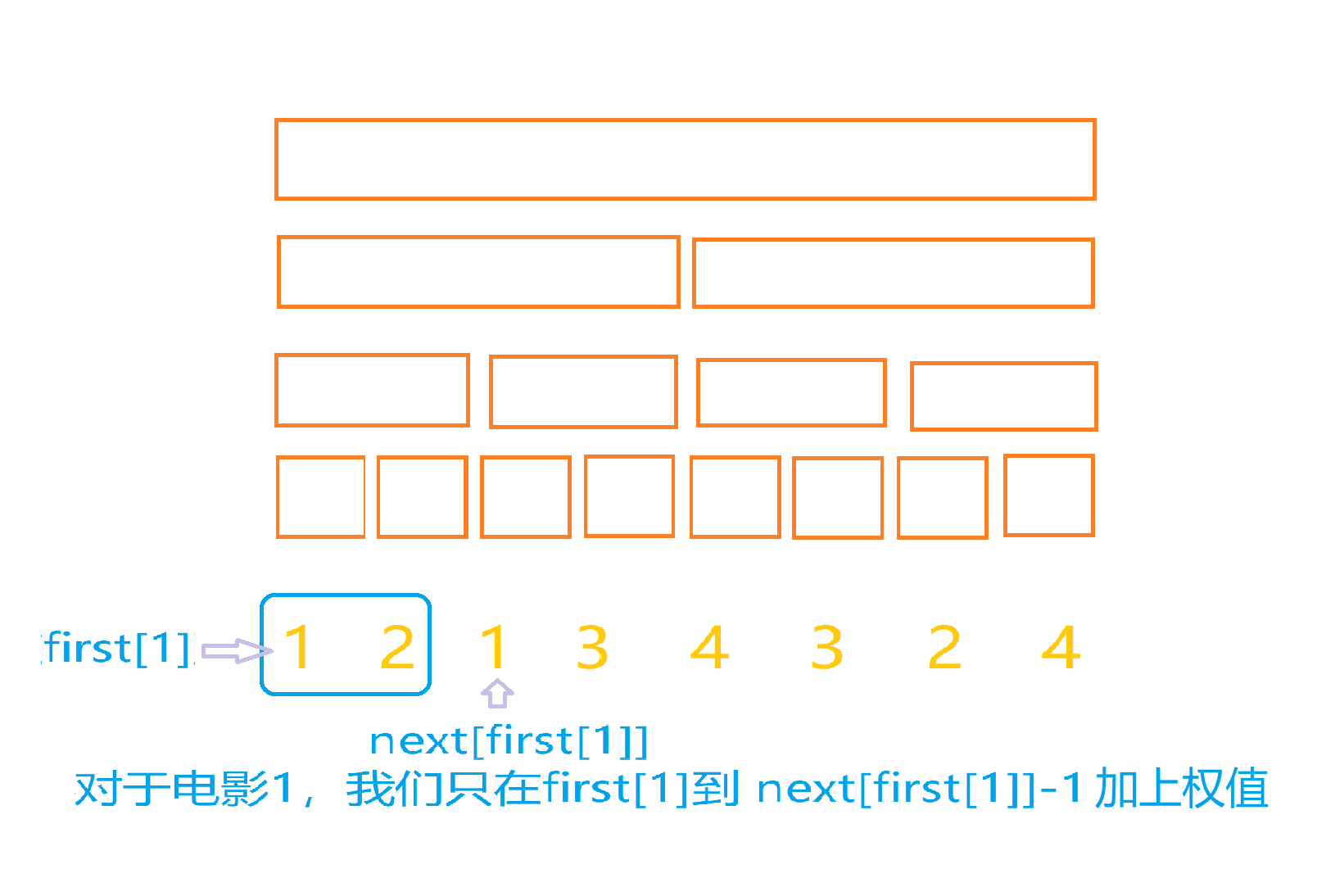
对于其他的电影也是同样的操作。

而在每一次左端点右移的修改当中，我们先设右移前，左端点为c，那么我们只要在[c,next[c]-1]减去有趣值,[next[c],next[next[c]]-1]加上有趣值就好了，这是为什么呢？我们看一下下面这个栗子：

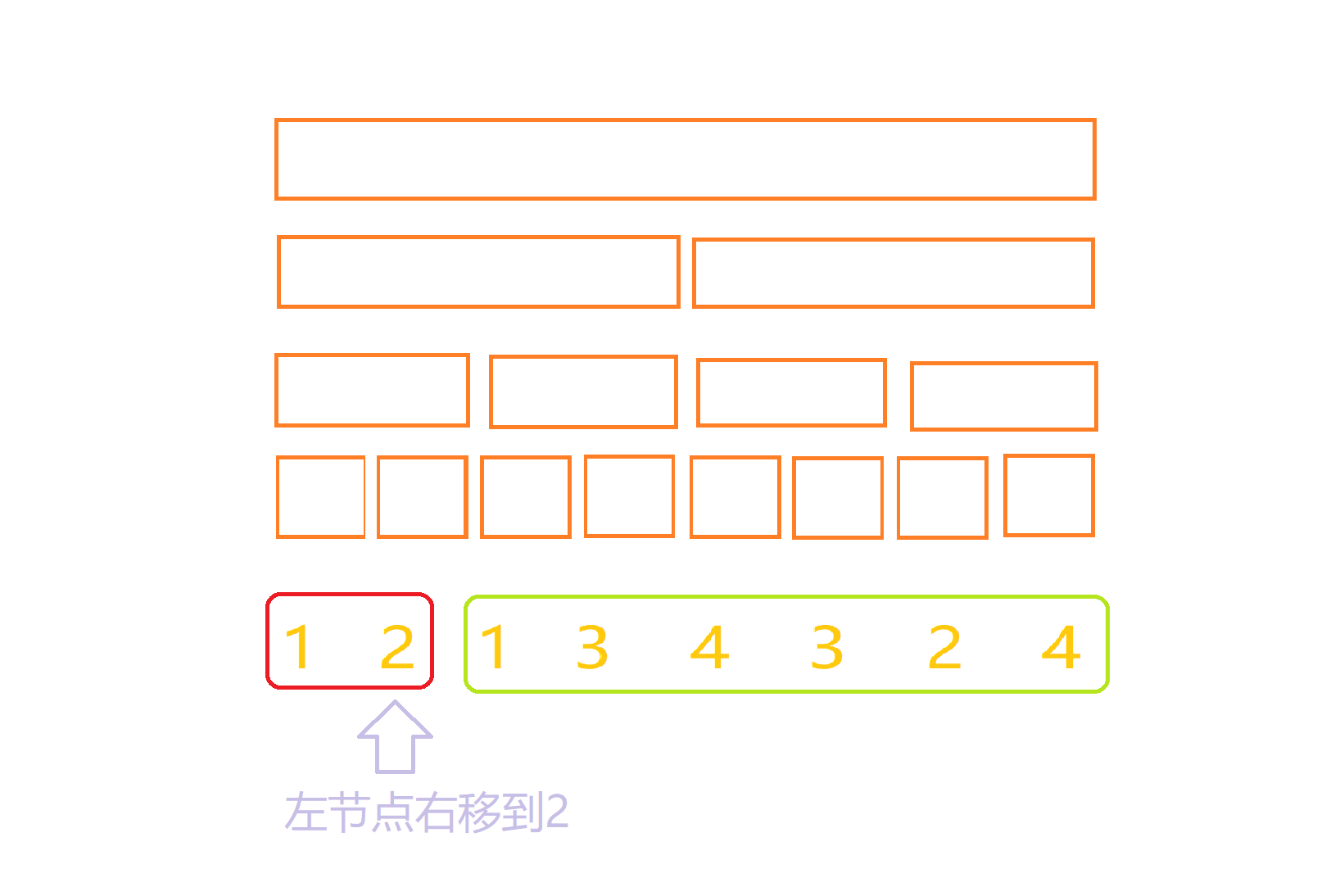
当我们的左节点从一移动到二时，红色框框之前不是加上了电影一的有趣值吗，现在第一个电影一已经没了，那么红色框对电影一的有趣值的加成就没有了，这时我们区间修改，对于红色框，即[c,next[c]-1]内的所有点减去电影的权值，再在绿色框框，也就是,[next[c],next[next[c]]-1]加上有趣值就好了。

所以在这样的一番操作下，这道题就变成了区间修改，区间最值查询的经典线段树题目了，在打lazy——tag的情况下，可以在 O(log n)完成单层的修改和查询，乘以对于左端点的枚举 O(n)，总的时间复杂度达到了预计的 O(n log n)。具体代码如下：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
int f[1100000],w[1100000],next[1100000],pre[1100000],first[1100000];
int i,j,k,m,n,o,p,jl,js,jk,x,y,z;
long long ma;

struct node
{
    long long max,tag;
}tr[4400000];

long long my_max(long long x,long long y)
{
    if(x>y)return x;
    else return y;
}

int change(int l,int r,int m)
{
    if(tr[m].tag!=0 && l!=r)
    {
        tr[m*2].max+=(tr[m].tag);tr[m*2].tag+=tr[m].tag;
        tr[m*2+1].max+=(tr[m].tag);tr[m*2+1].tag+=tr[m].tag;
        tr[m].tag=0;
    }
    if(l>=x && r<=y)
    {
        tr[m].max+=z;
        if(l!=r)
        {
            tr[m*2].max+=z;tr[m*2].tag+=z;
            tr[m*2+1].max+=z;tr[m*2+1].tag+=z;
        }
        return 0;
    }
    int mid=(l+r)/2;
    if(x<=mid)change(l,mid,m*2);
    if(y>mid)change(mid+1,r,m*2+1);
    tr[m].max=my_max(tr[m*2].max,tr[m*2+1].max);
    return 0;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&f[i]);
        if(first[f[i]]==0)first[f[i]]=i; 
        next[pre[f[i]]]=i;
        pre[f[i]]=i;
    }

    for(int i=1;i<=n;i++)if(next[i]==0)next[i]=n+1;

    for(int i=1;i<=m;i++)   
    {
        scanf("%d",&w[i]);
        if(first[i]>0)
        {
            x=first[i];y=next[first[i]]-1;z=w[i];
            change(1,n,1);
        }
    }

    ma=-214748364;
    for(int i=1;i<=n;i++)
    {
        ma=my_max(ma,tr[1].max);
        int c=f[i];
        x=i;y=next[i]-1;z=-w[c];
        change(1,n,1);
        x=next[i];y=next[next[i]]-1;z=w[c];
        change(1,n,1);
    }

    printf("%lld",ma);
    return 0;
}

结语

在这道经典例题中，我们发现了一个对于线段树构造的技巧——当我们不知道该如何构造的时候，试着去先把线段树的底层写出来，仅仅对于底层考虑要存储什么，毕竟上层线段树只是对下层节点的维护，如果底层构造好啦，剩下的问题也就迎刃而解了。希望你能对构造有所收获，希望你喜欢这篇BLOG！