在学习平衡树和Splay之前，我们应该了解一个更为基础的算法——二叉查找树。不论是平衡树还是splay都是建立在二叉查找树上，所以这篇BLOG，我就来带领你走进二叉查找树。

二叉查找树的定义

二叉查找数不同于普通二叉树的一个特点就是:对于每一个节点，若存在左子节点，那么该节点的值一定大于左子节点的值；若存在右子节点，那么该节点的值一定小于右子节点的值，例如下图就是一棵可爱的二叉查找树：

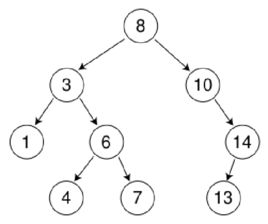
同时由于在二叉查找树中有上述的性质我们可以得出一个推论：对于每一棵二叉查找树，它的中序遍历就是树中数据从小到大排序过后的结果。

二叉查找树的运用

这篇BLOG，我们总点讲解一下二叉查找树的操作，毕竟平衡树实现的操作就是二叉查找树能实现的操作，所以在学习平衡树中，我们一定要熟练地掌握二叉查找树的各种操作。

假设我们现在有一个有序数列，那么查找可以运用折半、插值、斐波那契二等查找算法来实现，但是因为有序，在插入和删除操作上，如果采用上述方法，就需要耗费大量的时间（由于进行元素的移位），那么问题就来了，我们能否有一种既可以使得插入和删除效率不错，又可高效查找的数据结构和算法呢？

首先解决一个问题，如何使插入时不移动元素，我们可以想到链表，但是要保证其有序的话，首先得遍历链表寻找合适的位置，那么又如何高效的查找合适的位置呢，能否可以像二分一样，通过一次比较排除一部分元素。那么我们可以用二叉树的形式，以数据集第一个元素为根节点，之后将比根节点小的元素放在左子树中，将比根节点大的元素放在左子树中，在左右子树中同样采取此规则。

例如在上一幅图片中，就是由有序数列

1 3 4 6 7 8 10 13 14

得出来的二叉查找树：

那么在查找x时，若x比根节点小可以排除右子树所有元素，去左子树中查找（类似二分查找），这样查找的效率非常好，而且插入的时间复杂度为O（h），h为树的高度，较O（n）来说效率提高不少，但是在一些情景中，二叉查找树可能会退化成一条链，这时就需要运用一些旋转法则，让他不至于那么不平衡，这样就是我们后面才要将的平衡树了。

二叉查找树最完整的操作

在大部分的BLOG中，二叉查找树只有下面四种操作：

1.插入一个值为x的点
2.删除一个值为x的值
3.查找最大值
4.查找最小值

但在这篇BLOG中，我要告诉你二叉查找树最完整的八种操作：

1.插入一个值为x的点
2.删除一个值为x的值
3.查找最大值
4.查找最小值
4.查找排名为x的树
5.查找值为x的点的排名
6.求x的前驱(前驱定义为小于xx 且最大的数)
7.求x的后继(后继定义为大于xx 且最小的数)

定义结构

struct node
{
    int d,n,c,f,son[2];//d为值，f为父亲编号，c为控制的节点个数，n为同值节点的个数，son为左右子节点是谁
}tr[550000];int len,root; 

正常来说，我们若只要完成简单的四种操作，对于树上的每一个节点的左右儿子(son【2】),父亲是谁(f)和它本身的值(d)。

但是为了实现后面的四种更加高级操作，我们还要记录一下：
这个节点控制的节点个数，即以这个点为根的子树的大小(c)；
这个节点内部存了几个数(n)，即由于我们每个节点存储的值都不一样，我们与该节点的值相等的点都放在这个节点内，所以我们要记录一下有多少个点的值与该节点的值相同。

我们用结构体来实现一个点对多个数值的保存。

同样的，我们还要保存一下len——一共有多少个节点；root——整棵二叉查找树的根是谁。

更新控制的节点数

int update(int x)//更新x控制的节点数 
{
    int lc=tr[x].son[0];
    int rc=tr[x].son[1];
    tr[x].c=tr[lc].c+tr[rc].c+tr[x].n;
}

在每次插入或删除节点后，修改节点到根节点的一条链上的点的控制的节点的个数都会发生变化，为了保证我们存储的树上每个节点的c值都为正确的，就需要在每次修改后都将被修改节点到根节点的一条链上的点都更新一下控制的节点数。

添加一个节点

int add(int d,int f)//添加值为d的点，认f为父亲，f认它为孩子 
{
    len++;
    tr[len].d=d;tr[len].n=1;tr[len].c=1;
    tr[len].f=f; if(d<tr[f].d)tr[f].son[0]=len; else tr[f].son[1]=len;
    tr[len].son[0]=0;tr[len].son[1]=0;
}

在实现操作1，也就是插入一个值为x的点时，如果树上之前没有值为x的点，我们就要开创一个值为x的点。在这个模块中，我们就实现添加值为d的点，给这点初始化一下，然后认f为父亲，f认它为孩子。

查找节点地址

int findip(int d)//找值为d的节点的地址，PS：如果不存在值为d的点，就找接近d的点（可能大也可能小） 
{
    int x=root;
    while(tr[x].d!=d)
    {
        if(d<tr[x].d)
        {
            if (tr[x].son[0]==0) break;
            else x=tr[x].son[0];
        }
        else//if(d>tr[x].d) 
        {
            if (tr[x].son[1]==0) break;
            else x=tr[x].son[1];
        }
    } 
    return x;
}

在操作当中我们需要多次寻找值为d的点在哪（比如删除节点），或者接近d的值在哪（比如加入一个节点，找到后插到它的儿子位置就好了）。我们就只需要从root开始，一层层往下，由于我们知道在二叉查找树当中，每个节点的左子节点都小于它，右子节点都大于它。所以我们只要一层层判断向左儿子走，右儿子走还是不走（找到值一样的点 或者 没有对应的儿子了）就好了。

有了上面的铺垫以后

插入一个值

int ins(int d)//插入数值为d的点 
{
    if(root==0){ add(d,0); root=len; return 0; }
    int x=findip(d);

    if(tr[x].d==d)tr[x].n++;
    else add(d,x);
    while(x!=0)
    {
        update(x);
        x=tr[x].f;
    }
}

在插入一个值的时候，我们需要分两种情况进行讨论：

1.这棵树是空的

那么我们只要add一个点，然后root就是这点，就可以了。

2.这棵树不是空的

那么我们可以运用之前讲到的find函数，找到值为d的点在哪里。若存在值为d的点，那么直接这个点的n++就好了，代表多了一个这个值的点；若不存在值为d的点，这表示值为d的点应该出现在找到的这个点的儿子节点上，且这个儿子节点必为空，不然的话会继续findip()下去，找到的就不是这个点了。这个时候直接在找到点的对应儿子节点加上我们要添加的点就好了。

删除一个节点

删除一个节点在二叉查找树中是非常麻烦的，具体代码大概长这样：

int del(int d)
{
    int x=findip(d);
    tr[x].n--;tr[x].c--;
    if(tr[x].n>0)
    {
        while(x!=0)
        {
            update(x);
            x=tr[x].f;
        }
        return 0;
    }
    if(tr[x].son[0]==0 && tr[x].son[1]==0)
    {
        if(root==x)
        {
            root=0;
            len=0;
        }
        if(tr[tr[x].f].son[0]==x)tr[tr[x].f].son[0]=0;
        if(tr[tr[x].f].son[1]==x)tr[tr[x].f].son[1]=0;
        while(x!=0)
        {
            update(x);
            x=tr[x].f;

        }
        return 0;
    }

    else
    if(tr[x].son[0]!=0 && tr[x].son[1]==0)
    {
        if(root==x)root=tr[x].son[0];
        if(tr[tr[x].f].son[0]==x)tr[tr[x].f].son[0]=tr[x].son[0];
        if(tr[tr[x].f].son[1]==x)tr[tr[x].f].son[1]=tr[x].son[0];
        while(x!=0)
        {
            update(x);
            x=tr[x].f;

        }
        return 0;
    }

    else
    if(tr[x].son[0]==0 && tr[x].son[1]!=0)
    {
        if(root==x)root=tr[x].son[1];
        if(tr[tr[x].f].son[0]==x)tr[tr[x].f].son[0]=tr[x].son[1];
        if(tr[tr[x].f].son[1]==x)tr[tr[x].f].son[1]=tr[x].son[1];
        while(x!=0)
        {
            update(x);
            x=tr[x].f;

        }
        return 0;
    }

    else
    if(tr[x].son[0]!=0 && tr[x].son[1]!=0)
    {
        int y=tr[x].son[0];
        while(tr[y].son[1]!=0)y=tr[y].son[1];
        tr[x].n=tr[y].n;tr[y].n=1;
        del(tr[y].d);
        tr[x].d=tr[y].d;

        return 0;
    }

}

不要看它辣么辣么长，我们理一下思路也是很简单的，我们假设要删除x点，那么我们首先分为两大类进行讨论：

1.tr[x].n>1

即等于要删除值的点有多个，那就很简单了，直接n--，然后从这个点开始，向上一直到根节点每个节点update一下就好了，正如：

tr[x].n--;tr[x].c--;
        if(tr[x].n>0)
        {
            while(x!=0)
            {
                update(x);
                x=tr[x].f;
            }
            return 0;
        }

1.tr[x].n==1

这种情况就比较麻烦了，我们要细分为四种情况进行讨论：

1.这个节点没有左右儿子

这种情况也很好处理，如果这个点是根节点，它又没有左右儿子，这就意味着整棵树只有他这一个节点，那么直接把根设为空，节点数设为空就好了。

若它不是根节点，那么我们据只要判断一下他是它父亲节点的左儿子还是右节点，然后把它父亲对应的子节点设为空就好了。最后别忘了更新从这个点到根节点这条链上的子树大小，正如：

if(tr[x].son[0]==0 && tr[x].son[1]==0)
    {
        if(root==x)
        {
            root=0;
            len=0;
        }
        if(tr[tr[x].f].son[0]==x)tr[tr[x].f].son[0]=0;
        if(tr[tr[x].f].son[1]==x)tr[tr[x].f].son[1]=0;
        while(x!=0)
        {
            update(x);
            x=tr[x].f;

        }
        return 0;
    }

2.这个节点仅有左儿子

一样的，如果这个点是根节点，它只有左儿子，那么删除它以后，根就变成它的左儿子了。

若它不是根节点，那么我们据只要判断一下他是它父亲节点的左儿子还是右节点，然后把它父亲对应的子节点设为它的左儿子就好了。最后别忘了更新从这个点到根节点这条链上的子树大小，正如：

if(tr[x].son[0]!=0 && tr[x].son[1]==0)
    {
        if(root==x)root=tr[x].son[0];
        if(tr[tr[x].f].son[0]==x)tr[tr[x].f].son[0]=tr[x].son[0];
        if(tr[tr[x].f].son[1]==x)tr[tr[x].f].son[1]=tr[x].son[0];
        while(x!=0)
        {
            update(x);
            x=tr[x].f;

        }
        return 0;
    }

3.这个节点仅有右儿子

和上面一样，如果这个点是根节点，它只有右儿子，那么删除它以后，根就变成它的右儿子了。

若它不是根节点，那么我们据只要判断一下他是它父亲节点的左儿子还是右节点，然后把它父亲对应的子节点设为它的右儿子就好了。最后别忘了更新从这个点到根节点这条链上的子树大小，正如：

if(tr[x].son[0]==0 && tr[x].son[1]!=0)
    {
        if(root==x)root=tr[x].son[1];
        if(tr[tr[x].f].son[0]==x)tr[tr[x].f].son[0]=tr[x].son[1];
        if(tr[tr[x].f].son[1]==x)tr[tr[x].f].son[1]=tr[x].son[1];
        while(x!=0)
        {
            update(x);
            x=tr[x].f;

        }
        return 0;
    }

4.这个节点即有左儿子，又有右儿子

这种情况就比较复杂了，考虑我们现在有一棵二叉查找树，如下图：

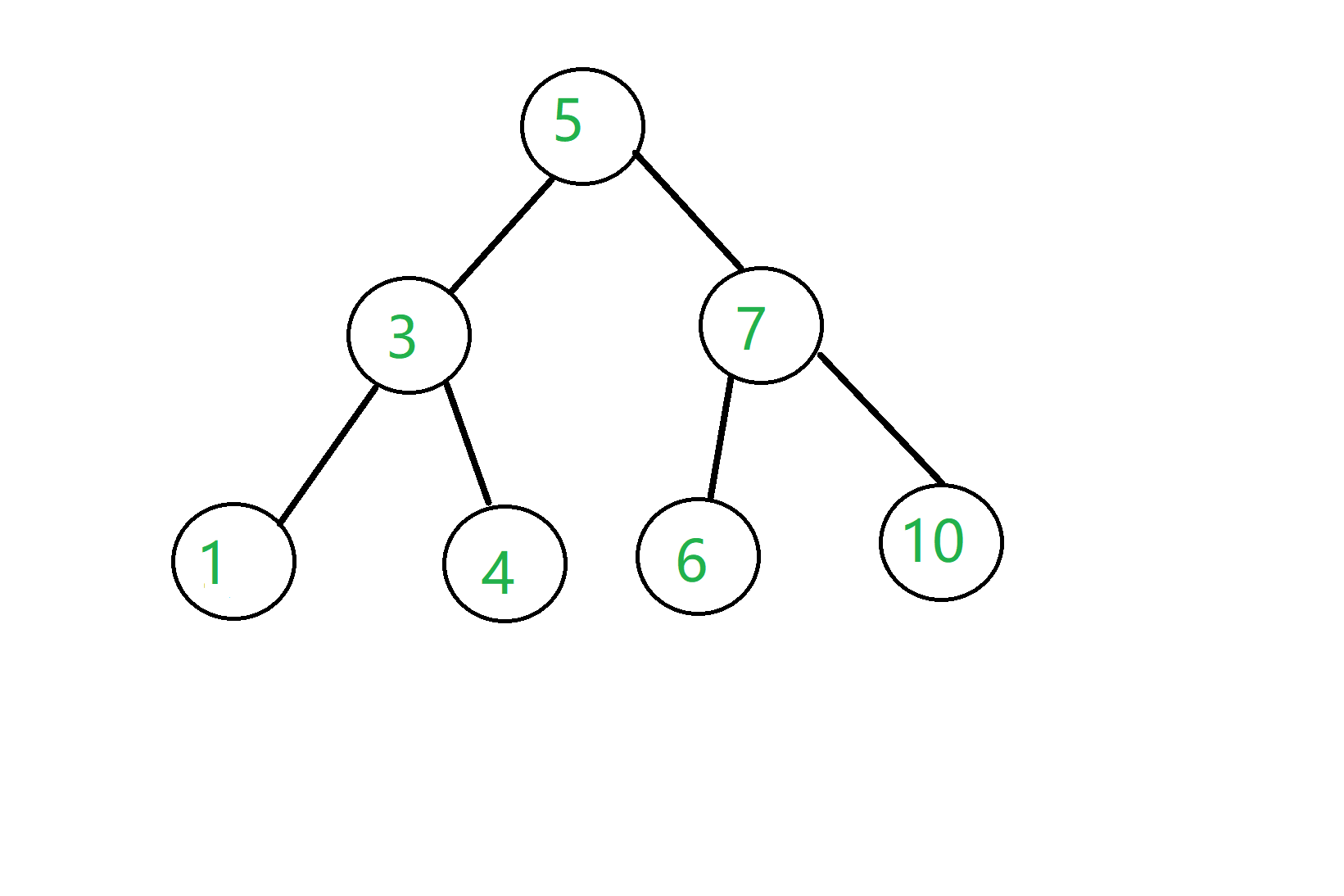
我们考虑把根节点删除，也就是把5给删除，那么我们就想，能不能找一个和5大小相近的树来顶替5呢？

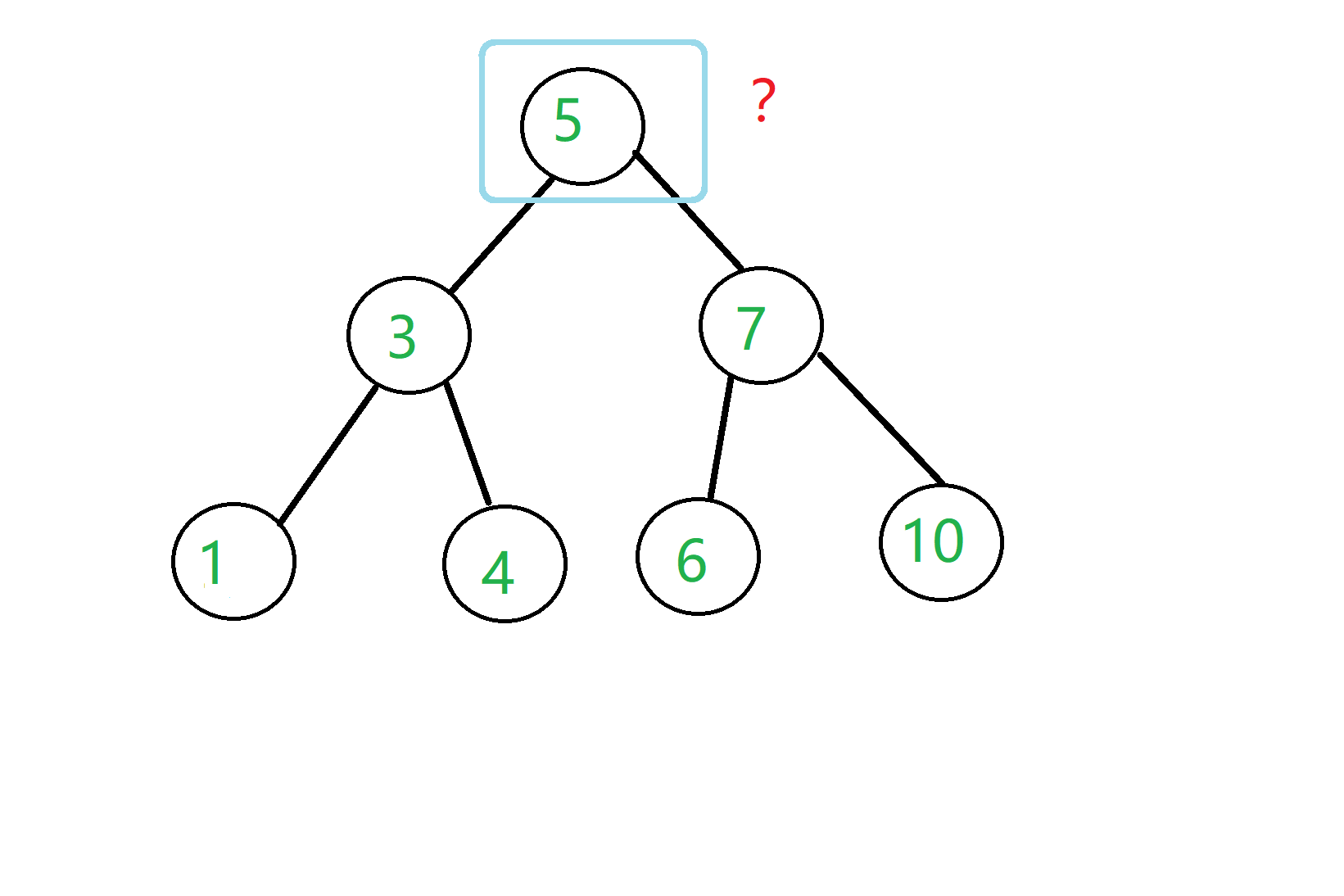
当然可以，我们发现把4和6放在5的位置后，这个二叉查找树的性质不发生改变！

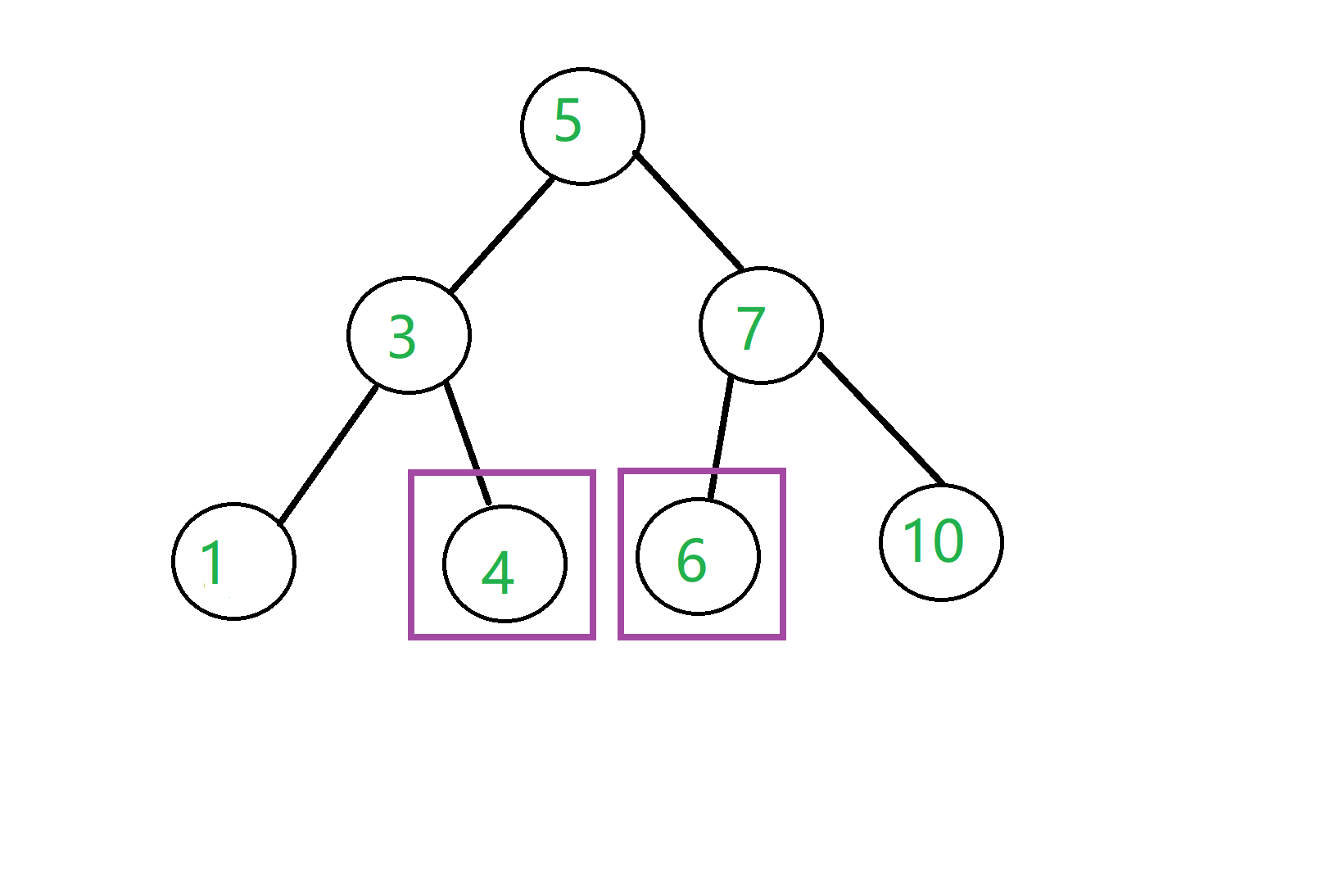
我们通过总结发现，当某一个节点被删除时，我们只需要把它左子树中最大的点，或者右子树最小的点放到删除点的位置，这颗二叉查找树的性质就不会发生改变，正如代码：

if(tr[x].son[0]!=0 && tr[x].son[1]!=0)
    {
        int y=tr[x].son[0];
        while(tr[y].son[1]!=0)y=tr[y].son[1];
        tr[x].n=tr[y].n;tr[y].n=1;
        del(tr[y].d);
        tr[x].d=tr[y].d;

        return 0;

查找一个数的排名

int findpaiming(int d)//寻找值为d的点的排名 
{
    int x=findip(d),y=tr[x].f;
    int ans=tr[tr[x].son[0]].c+1;

    while(y!=0 )
    {
        if(tr[y].son[1]==x)
        {
          ans+=tr[y].n;
          ans+=tr[tr[y].son[0]].c;
        }
        x=y;
        y=tr[y].f;
    }
    return(ans);
}

要寻找一个数的排名，我们就只要去找有多少个点比他小，再加一就是答案了。那么我们回到一棵二叉查找树的任意一个节点，有哪些点比它小呢？

我们看一下下面这副图，有哪些点比粉红色的点要小呢？

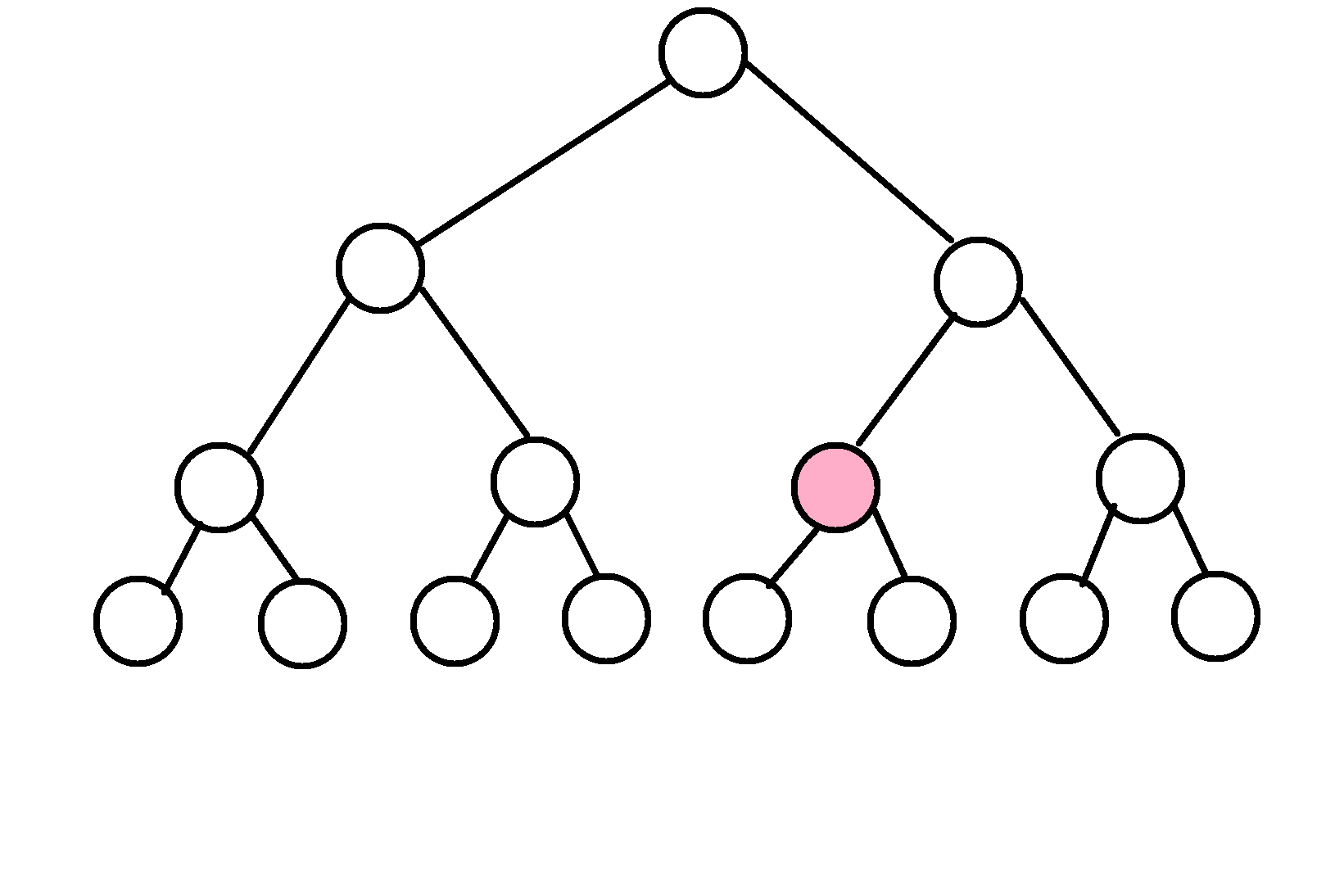
我们通过分析发现，绿色的点的值都比粉色的值要小：

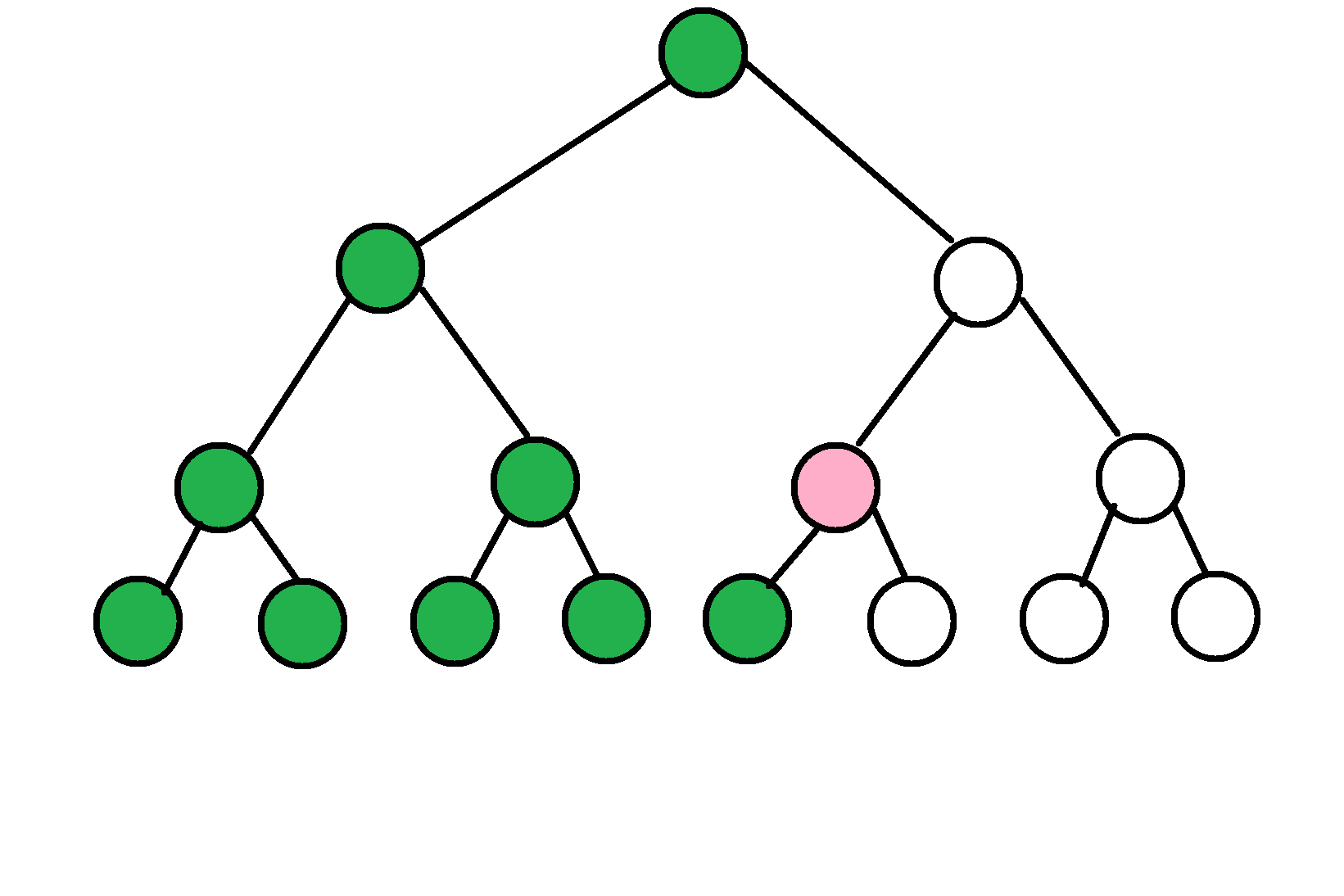
我们再通过分析，发现这些绿色的节点都分布在哪里呢？
首先查询点的左子树一定比他小这个毋庸置疑，接着我们枚举一下查询点的父亲到根节点的那条链上的每个点，如果粉色点在我们枚举的点的右子树上，就代表我们粉色的点大于我们枚举到的这个点和它的整个左子树，这时我们只要加上这个点包含的点数和它的整个左子树包含的点数就好了：

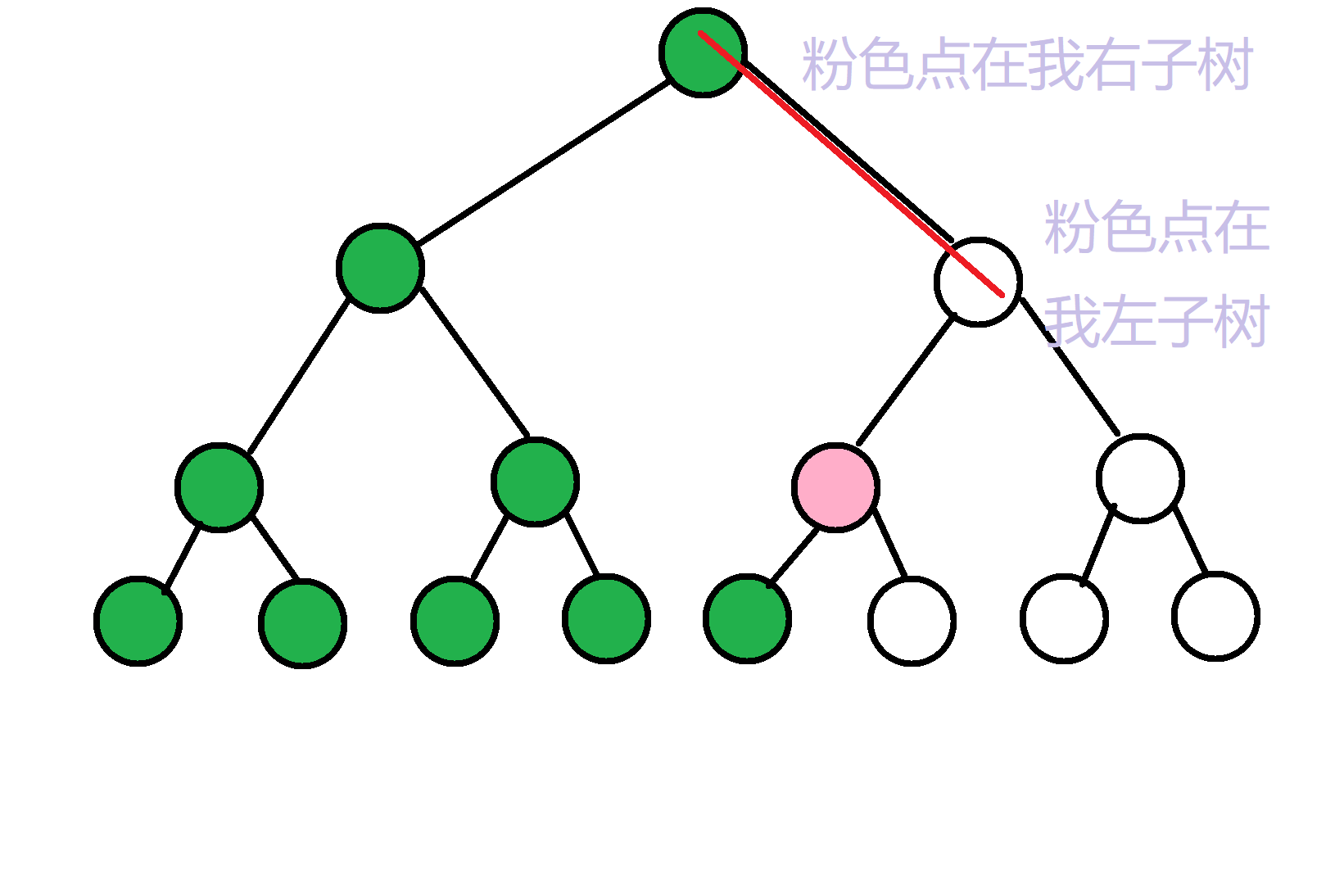
所以代码就很显然了。

查找排名对应的数

int findshuzi(int k)//寻找排名为d的点的值
{
    int x=root;
    while(1) 
    {
        int lc=tr[x].son[0],rc=tr[x].son[1];
             if(k<=tr[lc].c) x=lc;
        else if(k>tr[lc].c+tr[x].n){k=k-tr[lc].c-tr[x].n;x=rc;}
        else break;
    }
    return(tr[x].d);
} 

一样的，我们要查询排名为x的数，那么我们就从根节点出发，遇到每一个节点都问一下这个点包含了多少个点啊，我们记为n，这个点的左子树有多少个点啊，我们记为l，这个右子树包含了多少点啊，我们记为r。

那么如果我们的k<=l,那就不用怀疑了，我们要查找的数在左子树里，且在左子树里也是第k大，递归去找左子树就好了。

如果我们的k>l+n,那么也不用怀疑了，这个点不可能在左子树和这个点上了，一定出现在右子树，且在右子树的排名为k-tr[lc].c-tr[x].n，注意，是k-tr[lc].c-tr[x].n，不是第k!!!这时我们递归去找右子树就好了。

剩下的情况呢？不在左子树也不在右子树，那是我们现在到的这个点了呀！直接输出就可以了！

查找一个数的前驱

int findqianqu(int d)
{
    ins(d);
    int x=findip(d);
    if(tr[x].son[0]!=0)
    {
        x=tr[x].son[0];
        while(tr[x].son[1]!=0)x=tr[x].son[1];
    }
    else
    {
        while(tr[tr[x].f].son[1]!=x && x!=0)x=tr[x].f;
        x=tr[x].f;
    }
    del(d);
    return (tr[x].d);
}

首先我们要查找的数，不一定在我们的二叉查找树上，我们先把问题简化：如果要查找一个二叉查找树上的点的前驱值，怎么找？

我们分两种情况：
1.若一个节点有左子树，那么该节点的前驱节点是其左子树中val值最大的节点（也就是左子树中所谓的rightMostNode）

2.若一个节点没有左子树，那么判断该节点和其父节点的关系

1 若该节点是其父节点的右边孩子，那么该节点的前驱结点即为其父节点。
2 若该节点是其父节点的左边孩子，那么需要沿着其父亲节点一直向树的顶端寻找，直到找到一个节点P，P节点是其父节点Q的右边孩子，那么Q就是该节点的后继节点

这样我们就能解决查找一个二叉查找树上的点的前驱值，但是我们的目标是查找任意一个值的前驱值，怎么办？那还不简单，我们只要先插入一个这个值，再去查找一个二叉查找树上的点的前驱值，最后我们再删除这个点就好了。

查找一个数的后继

int findhouji(int d)
{
    ins(d);
    int x=findip(d);
    if(tr[x].son[1]!=0)
    {
        x=tr[x].son[1];
        while(tr[x].son[0]!=0)x=tr[x].son[0];
    }
    else
    {
        while(tr[tr[x].f].son[0]!=x && x!=0)x=tr[x].f;
        x=tr[x].f;
    }
    del(d);
    return (tr[x].d);
}

和找前驱一样，我们先简化一下问题：如果要查找一个二叉查找树上的点的后继值，怎么找？

我们仍然分两种情况：

1.若一个节点有右子树，那么该节点的后继节点是其右子树中val值最小的节点（也就是右子树中所谓的leftMostNode）

2.若一个节点没有右子树，那么判断该节点和其父节点的关系

1 若该节点是其父节点的左边孩子，那么该节点的后继结点即为其父节点
2 若该节点是其父节点的右边孩子，那么需要沿着其父亲节点一直向树的顶端寻找，直到找到一个节点P，P节点是其父节点Q的左边孩子（可参考例子2的前驱结点是1），那么Q就是该节点的后继节点

同样的，我们把要查找的值插入到我们的二叉查找树中，再按照上面的规则进行查找就好了，最后别忘了删除这个临时节点。

到这里我们的八种操作就实现完了。

经典例题

【luogu p3369】
题目描述
您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

插入 xx 数
删除 xx 数(若有多个相同的数，因只删除一个)
查询 xx 数的排名(排名定义为比当前数小的数的个数 +1+1 。若有多个相同的数，因输出最小的排名)
查询排名为 xx 的数
求 xx 的前驱(前驱定义为小于 xx ，且最大的数)
求 xx 的后继(后继定义为大于 xx ，且最小的数)
输入输出格式
输入格式：
第一行为 nn ，表示操作的个数,下面 nn 行每行有两个数 optopt 和 xx ， optopt 表示操作的序号( 1 \leq opt \leq 6 1≤opt≤6 )

输出格式：
对于操作 3,4,5,63,4,5,6 每行输出一个数，表示对应答案

输入输出样例
输入样例#1：
10
1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598
输出样例#1：
106465
84185
492737
说明
时空限制：1000ms,128M

1.n的数据范围： n \leq 100000 n≤100000

2.每个数的数据范围： [-{10}^7, {10}^7][−10
7
,10
7
]

有人可能要问了，这不是一道平衡树的题目吗，为什么可以用二叉查找树呢？没错，你要明白，平衡树的本质是二叉查找树，而平衡操作只是为了让这颗二叉查找树不至于退化成一条链，是为了加速二叉查找树，从本质上来说还是一棵二叉查找树，所以平衡树能做的题，二叉查找树也能做，不过会比较慢，这里就是我们上面讲的八种操作，代码如下：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
struct node
{
    int d,n,c,f,son[2];
}tr[550000];int len,root;//d为值，f为父亲编号，c为控制的节点个数，n为同值节点的个数 

int update(int x)//更新x控制的节点数 
{
    int lc=tr[x].son[0];
    int rc=tr[x].son[1];
    tr[x].c=tr[lc].c+tr[rc].c+tr[x].n;
}

int add(int d,int f)//添加值为d的点，认f为父亲，f认它为孩子 
{
    len++;
    tr[len].d=d;tr[len].n=1;tr[len].c=1;
    tr[len].f=f; if(d<tr[f].d)tr[f].son[0]=len; else tr[f].son[1]=len;
    tr[len].son[0]=0;tr[len].son[1]=0;
}

int findip(int d)//找值为d的节点的地址，PS：如果不存在值为d的点，就找接近d的点（可能大也可能小） 
{
    int x=root;
    while(tr[x].d!=d)
    {
        if(d<tr[x].d)
        {
            if (tr[x].son[0]==0) break;
            else x=tr[x].son[0];
        }
        else//if(d>tr[x].d) 
        {
            if (tr[x].son[1]==0) break;
            else x=tr[x].son[1];
        }
    } 
    return x;
}

int ins(int d)//插入数值为d的点 
{
    if(root==0){ add(d,0); root=len; return 0; }
    int x=findip(d);

    if(tr[x].d==d)tr[x].n++;
    else add(d,x);
    while(x!=0)
    {
        update(x);
        x=tr[x].f;
    }
}

int del(int d)
{
    int x=findip(d);
    tr[x].n--;tr[x].c--;
    if(tr[x].n>0)
    {
        while(x!=0)
        {
            update(x);
            x=tr[x].f;
        }
        return 0;
    }
    if(tr[x].son[0]==0 && tr[x].son[1]==0)
    {
        if(root==x)
        {
            root=0;
            len=0;
        }
        if(tr[tr[x].f].son[0]==x)tr[tr[x].f].son[0]=0;
        if(tr[tr[x].f].son[1]==x)tr[tr[x].f].son[1]=0;
        while(x!=0)
        {
            update(x);
            x=tr[x].f;

        }
        return 0;
    }

    else
    if(tr[x].son[0]!=0 && tr[x].son[1]==0)
    {
        if(root==x)root=tr[x].son[0];
        if(tr[tr[x].f].son[0]==x)tr[tr[x].f].son[0]=tr[x].son[0];
        if(tr[tr[x].f].son[1]==x)tr[tr[x].f].son[1]=tr[x].son[0];
        while(x!=0)
        {
            update(x);
            x=tr[x].f;

        }
        return 0;
    }

    else
    if(tr[x].son[0]==0 && tr[x].son[1]!=0)
    {
        if(root==x)root=tr[x].son[1];
        if(tr[tr[x].f].son[0]==x)tr[tr[x].f].son[0]=tr[x].son[1];
        if(tr[tr[x].f].son[1]==x)tr[tr[x].f].son[1]=tr[x].son[1];
        while(x!=0)
        {
            update(x);
            x=tr[x].f;

        }
        return 0;
    }

    else
    if(tr[x].son[0]!=0 && tr[x].son[1]!=0)
    {
        int y=tr[x].son[0];
        while(tr[y].son[1]!=0)y=tr[y].son[1];
        tr[x].n=tr[y].n;tr[y].n=1;
        del(tr[y].d);
        tr[x].d=tr[y].d;

        return 0;
    }

}

int findpaiming(int d)//寻找值为d的点的排名 
{
    int x=findip(d),y=tr[x].f;
    int ans=tr[tr[x].son[0]].c+1;

    while(y!=0 )
    {
        if(tr[y].son[1]==x)
        {
          ans+=tr[y].n;
          ans+=tr[tr[y].son[0]].c;
        }
        x=y;
        y=tr[y].f;
    }
    return(ans);
}

int findshuzi(int k)//寻找排名为d的点的值
{
    int x=root;
    while(1) 
    {
        int lc=tr[x].son[0],rc=tr[x].son[1];
             if(k<=tr[lc].c) x=lc;
        else if(k>tr[lc].c+tr[x].n){k=k-tr[lc].c-tr[x].n;x=rc;}
        else break;
    }
    return(tr[x].d);
} 

int findqianqu(int d)
{
    ins(d);
    int x=findip(d);
    if(tr[x].son[0]!=0)
    {
        x=tr[x].son[0];
        while(tr[x].son[1]!=0)x=tr[x].son[1];
    }
    else
    {
        while(tr[tr[x].f].son[1]!=x && x!=0)x=tr[x].f;
        x=tr[x].f;
    }
    del(d);
    return (tr[x].d);
}

int findhouji(int d)
{
    ins(d);
    int x=findip(d);
    if(tr[x].son[1]!=0)
    {
        x=tr[x].son[1];
        while(tr[x].son[0]!=0)x=tr[x].son[0];
    }
    else
    {
        while(tr[tr[x].f].son[0]!=x && x!=0)x=tr[x].f;
        x=tr[x].f;
    }
    del(d);
    return (tr[x].d);
}

int main()
{
    int n;
    scanf("%d",&n);
    root=0;
    for(int i=1;i<=n;i++)
    {
        int cz,x;
        tr[0].c=0;
        scanf("%d%d",&cz,&x);
        if(cz==1)ins(x);
        if(cz==2)del(x);
        if(cz==3)printf("%d\n",findpaiming(x));
        if(cz==4)printf("%d\n",findshuzi(x));
        if(cz==5)printf("%d\n",findqianqu(x));
        if(cz==6)printf("%d\n",findhouji(x));
    }
    return(0);

}

结语

用完全不旋转的二叉查找树去实现平衡树的功能确实特别复杂，也很难调，但确实是训练码力的一个好途径，希望你能彻底了解二叉查找树，希望你能喜欢这篇BLOG！