说到线段树，大家第一反应就是经典的RMQ问题，相信大家都已经很好的掌握了，今天就不再过多的进行讲解了。今天我们主要通过一道例题开始，浅谈一下线段树的构造吧。

一道水题

我们先从一道简单的例题看起。

给你一段长为n，n≤1e5 的47串，比如4747747444774…………，求这个串的最长不下降子序列的长度是多少(PS 子序列即不一定要连续的串)。

“这不是一道惊天大水题吗”看完后的你一定如此振臂高呼。确实，这套题只要写个DP,DP[i]表示在到i个字符时，1-i的最长子串是多长，直接转移记录一下上一个出现的4和7在哪，就可以在O(n)的时间复杂度内解决这道题了。

我们换一个角度来考虑，我们也可以枚举转折点。何谓转折点，即我们最后得出的答案是一个47串，即开始时为x个4，后面接着y个7，那我们就只要枚举第一个7出现在哪里就好了。

问题就出现在，如果我们当前在长为l的序列中，枚举到在第i个位置出现了第一个7，那么我们应该如何快速求解【1，i）中有多少个4，【i，n】有多少个7。方法当然也很多，我们可以用前缀和达到单次O(1)的复杂度，或者用线段树维护区间的4，7数量，也能达到单次O(log n)的时间复杂度。

两道水题

我们把上面的例题稍作修改：

给你一段长为长为n，n≤1e5 的47串，比如4747747444774…………，给你m个操作，m≤1e5，要求支持两种操作：
1.求整个串的最长不下降子序列的长度是多少
2.读入一个x，将序号为x的数4改为7，7改为4

在这种情况下，由于出现了修改，DP 和 枚举转折点+前缀和 都出现了一个问题，修改和查询都变成了O(n)，所以总的时间复杂度达到了O(mn),是铁定TLE的。

但是我们的线段树没有倒下。我们考虑一下线段树，我们要求的是整个串的最长不下降子序列，而最长不下降的子序列一共只要三种情况：全部是4，全部是7，或者是47串（即开始时为x个4，后面接着y个7，我们默认x，y均大于0）。

这时我们就想，我们拿线段树来维护什么？我们要求全部是4，全部是7，或者是47串的最长长度，那么我们就顺水推舟，维护一下每个区间4的数量，7的数量，或者47串的最长长度。

下面我们来带入一个栗子进行讲解：
比如我们有一个串,我们先开好线段树，把底层的节点先构造好：

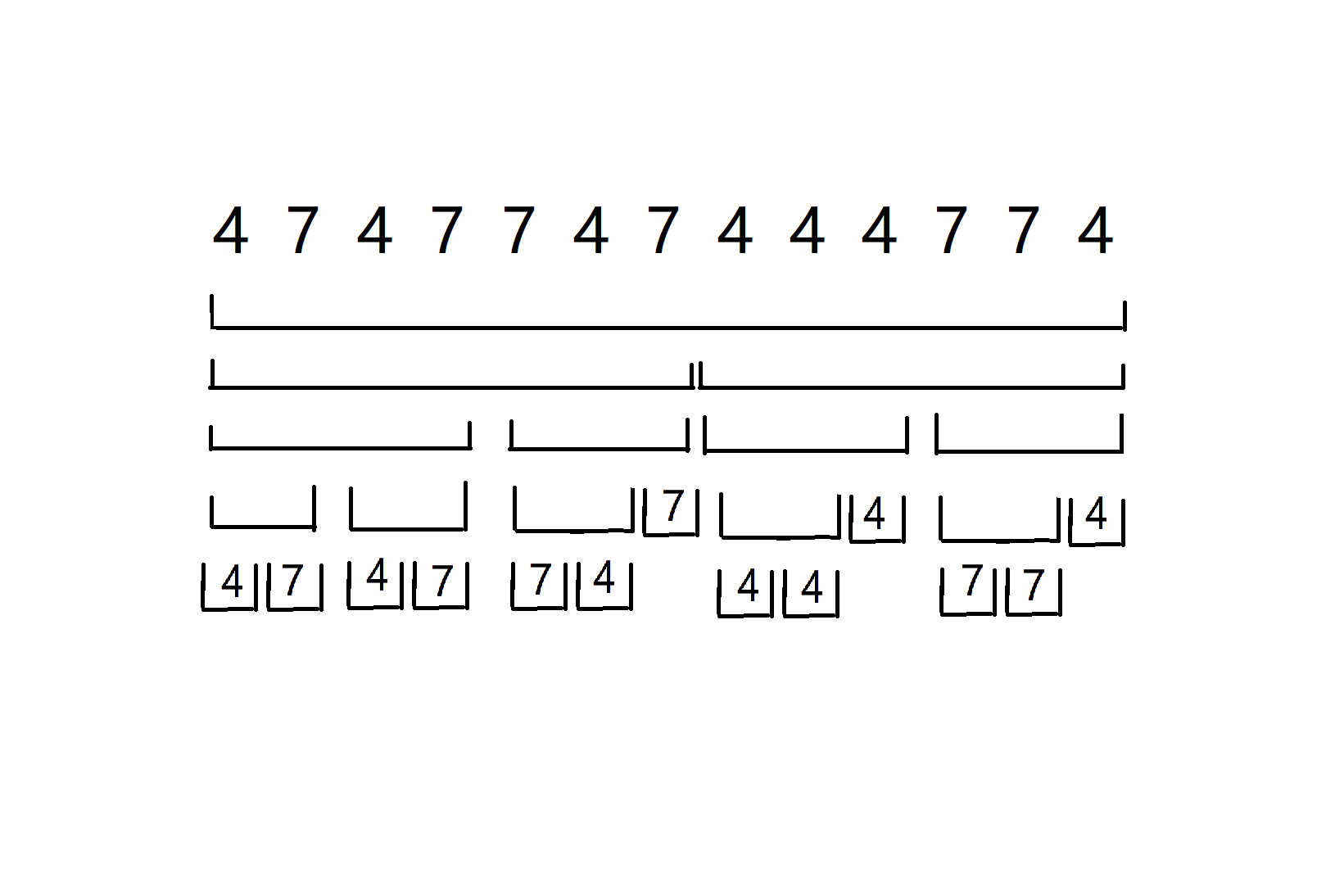
接下来，我们维护每个区间4的数量，7的数量，以及47串的最长长度，我们先搞出一层：

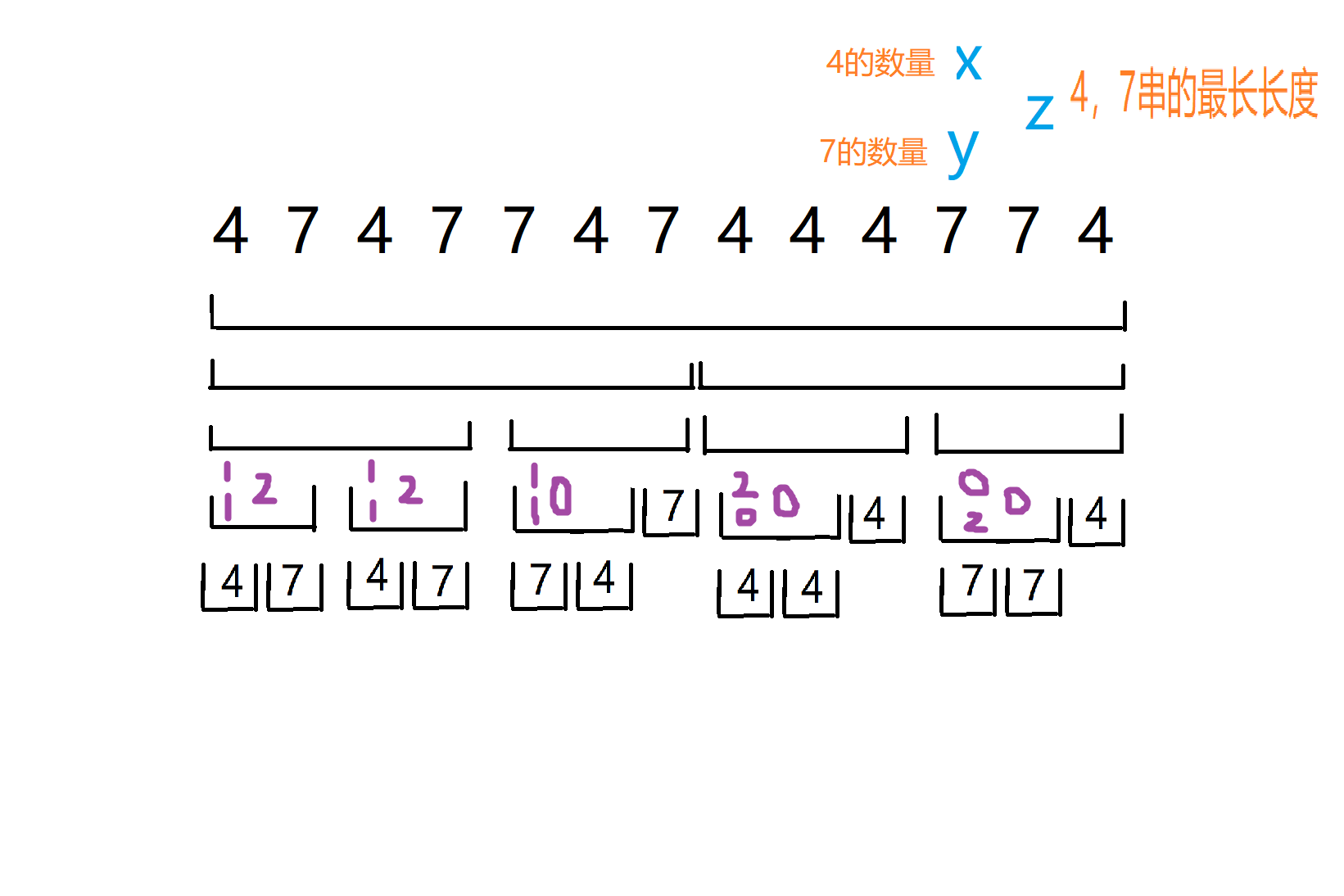
4和7的数量都很好维护，直接等于两个子区间的4，7数量相加。但是47的数量呢？由于我们约定了，47串是开始时为x个4，后面接着y个7，且x，y均大于0，故47串的长度分为3大类：

1.左子区间4的数量+右子区间7的数量
2.左子区间47串的最长长度+右子区间7的数量
3.左子区间4的数量+右子区间47串的最长长度
这三个取max即为47串在这个区间内的最长的长度。

这道题就迎刃而解了。接下来是解决修改的问题：修改就很简单了，从底层开始逐层修改即可，由于是单点修改，故不需要打lazy-tag。

三道水题

我们再对上题进行一点点修改：

给你一段长为长为n，n≤1e5 的47串，比如4747747444774…………，给你m个操作，m≤1e5，要求支持两种操作：
1.读入一对x，y求子串【x，y】中的最长不下降子序列的长度是多少
2.读入一个x，将序号为x的数4改为7，7改为4

有了上一题的基础，这道题也不难了，我们发现【x，y】所对应的子串就是线段树中几个零散的区间拼凑而成。，大概如下:

接下来就很简单了，我们可以直接枚举转折点，即第一个7出现在哪个串，比如如果我们枚举到出现在第3个串：

那么此时的最长不下降子序列的长度为：块1的4的数量+块2的4的数量+块3的47的最长长度+块4的7的数量。

修改还是和上面那道题一模一样。

四道水题

我们继续修改题目：

给你一段长为长为n，n≤1e5 的47串，比如4747747444774…………，给你m个操作，m≤1e5，要求支持三种操作：
1.读入一对x，y求子串【x，y】中的最长不下降子序列的长度是多少
2.读入一个x，将序号为x的数4改为7，7改为4
3.读入一对【x，y】，将【x，y】中的4全部变为7，7全部变为4。

这道题多给出我们一个要求：要求完成区间的翻转：将【x，y】中的4全部变为7，7全部变为4。说到区间修改，大部分人的第一反应就是打lazy-tag。没错，打完tag后，4和7的数量都很好变化，翻转过会，直接把4的数量给7，7的数量给4。

但是47串呢？嗯，是个问题。要得到翻转后的47串的最长长度，我们就要知道翻转前74串的最长长度。那就很显然了呀。我们只要多维护一个数据——74串的最长长度就行了。在每次翻转时，把该区间的47串长度给74串，74串长度给47串就行了，而74串的求法和47串大同小异，这里就不过多讲解了。

同理，如果题目要求把一段区间全部变为4或7也是一样的。

修改也是换汤不换药，也不过多讲解了。

五道水题

我们最后再对题目进行一下修改：

给你一段长为长为n，n≤1e5 的47串，比如4747747444774…………，给你m个操作，m≤1e5，要求支持三种操作：
1.读入一对x，y求子串【x，y】中的最长不下降子串的长度是多少（子串要求各个字符相连）
2.读入一个x，将序号为x的数4改为7，7改为4
3.读入一对【x，y】，将【x，y】中的4全部变为7，7全部变为4。

这道题要求我们求解的是最长不下降子串的长度，那么我们维护的东西就要进行修改了，我们还是先把底层的线段树给构造出来：

我们考虑一些，由于是要求子串，所以4，7在开头的位置就很重要了。这次我们对于每一个线段树对应的区间，考虑维护五个值：

1.以4为开头的最长不下降子串的长度
2.以7为开头的最长不下降子串的长度
3.以4为结尾的最长不下降子串的长度
4.以7为结尾的最长不下降子串的长度
5.该区间内最长不下降子串的长度

接下来我们考虑如何维护，考虑对于每一个非底层区间，都有左右两个子区间：

这时以4开头的最长不下降子串长度就要分情况讨论了:

1:如果在左子区间内，以4开头的最长不下降子串贯穿了整个左子区间，即整个左子区间都是以4开头的最长不下降序列，那么如果此时左子区间以4结尾，我们就只要用左子串的长度+右子串中以4开头的最长不下降子串长度；否则，如果如果此时左子区间以7结尾，我们就只要用左子串的长度+右子串中以7开头的最长不下降子串长度。

2.如果在左子区间内，以4开头的最长不下降子串仅仅自是左子区间的一部分，那么就无法连接到右子区间，此时我们的值就是 左子串中以4开头的最长不下降序列的长度。

以7为开头的最长不下降子串的长度，以4为结尾的最长不下降子串的长度，以7为结尾的最长不下降子串的长度也是一样的道理就不再多做解释了。

接下来我们要解决该区间内最长不下降子串的长度。我们发现此时最长不下降子串分为三种情况：

1.全部在左区间中：

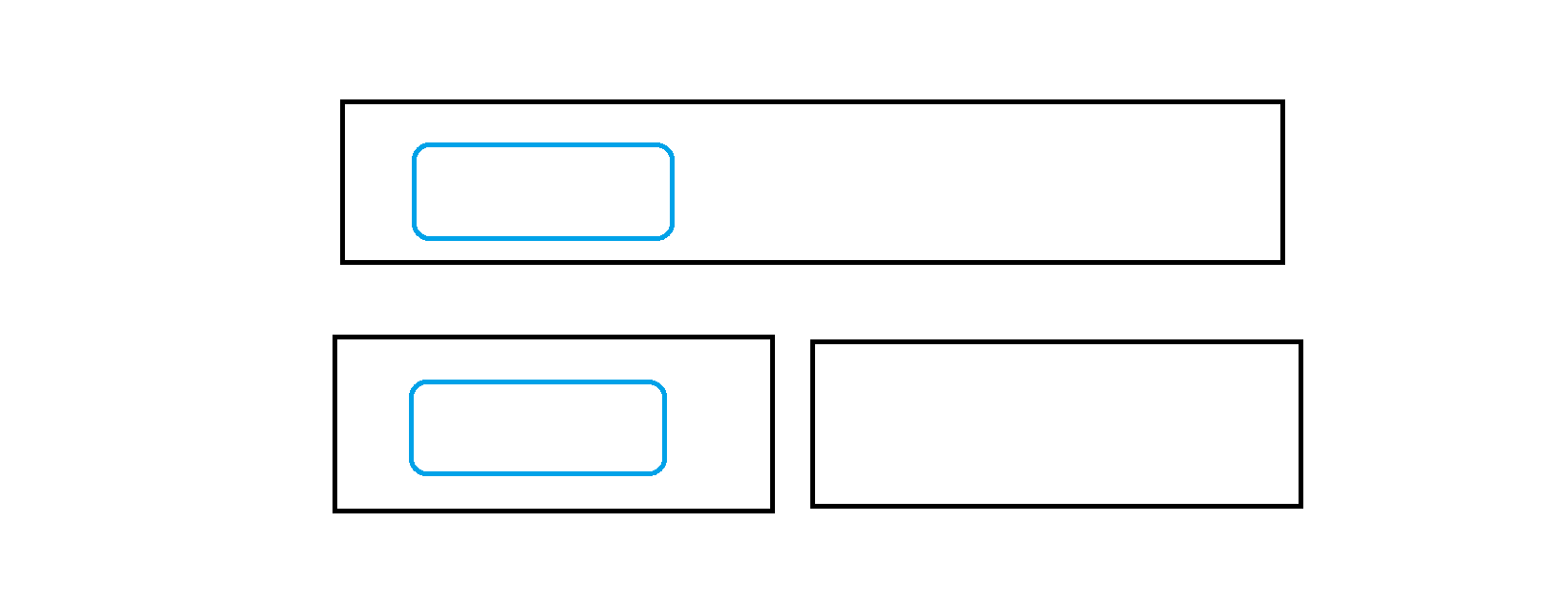
那么此时最长不下降子串的长度就为左子区间内最长不下降子串的长度。

2.全部在右区间中：

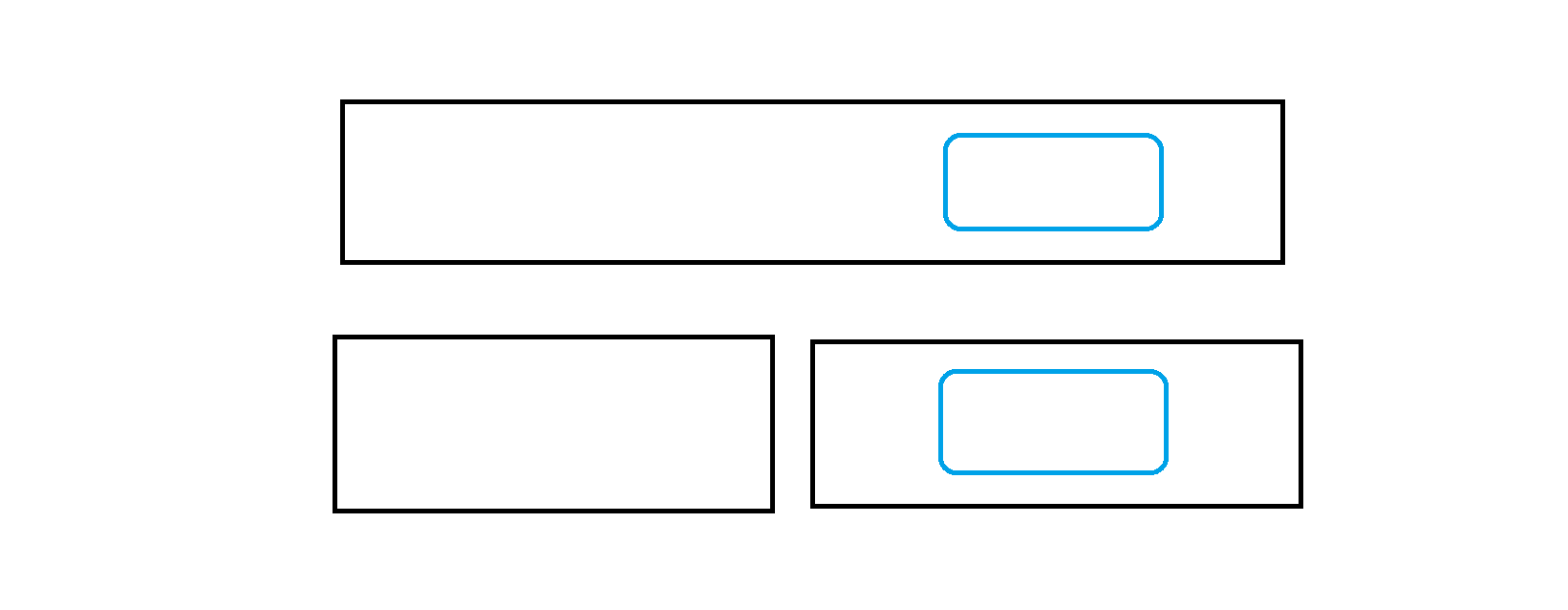
那么此时最长不下降子串的长度就为右子区间内最长不下降子串的长度。

3.横跨左右两个区间

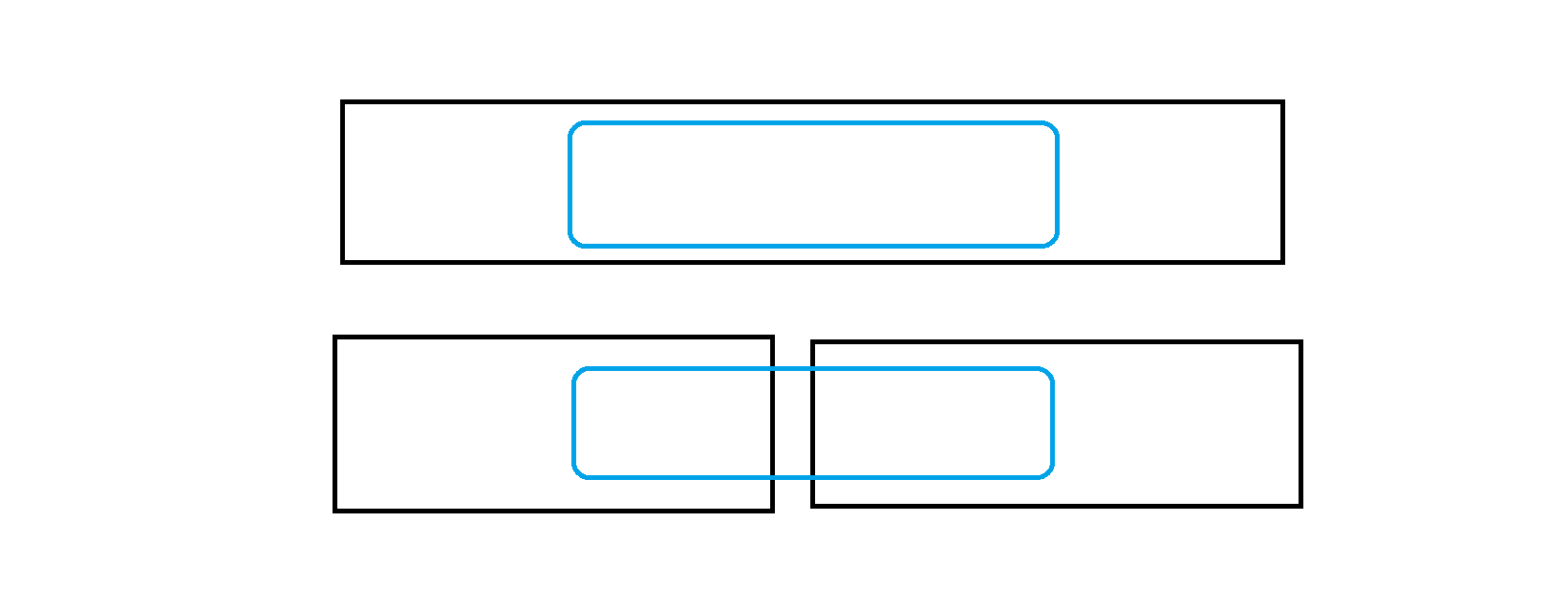
这时我们又要分三种情况讨论：

1.左子区间以4结尾，右子区间以4开头；此时最长不下降子串的长度就为：
左子区间内以4结尾的最长不下降子串的长度+右子区间内以4开头的最长不下降子串的长度。

2.左子区间以4结尾，右子区间以7开头；此时最长不下降子串的长度就为：
左子区间内以4结尾的最长不下降子串的长度+右子区间内以7开头的最长不下降子串的长度。

左子区间以7结尾，右子区间以7开头；此时最长不下降子串的长度就为：
左子区间内以7结尾的最长不下降子串的长度+右子区间内以7开头的最长不下降子串的长度。

左子区间以7结尾，右子区间以4开头；此时不满足题目对于不下降的要求，故不存在。

最后我们比较

1.以4为开头的最长不下降子串的长度
2.以7为开头的最长不下降子串的长度
3.以4为结尾的最长不下降子串的长度
4.以7为结尾的最长不下降子串的长度
5，该区间内最长不下降子串的长度

得出其中的最大值输出就可以了。

结语

通过上面的五个水题，我们可以清晰地认识到，线段树是由三大部分组成的：

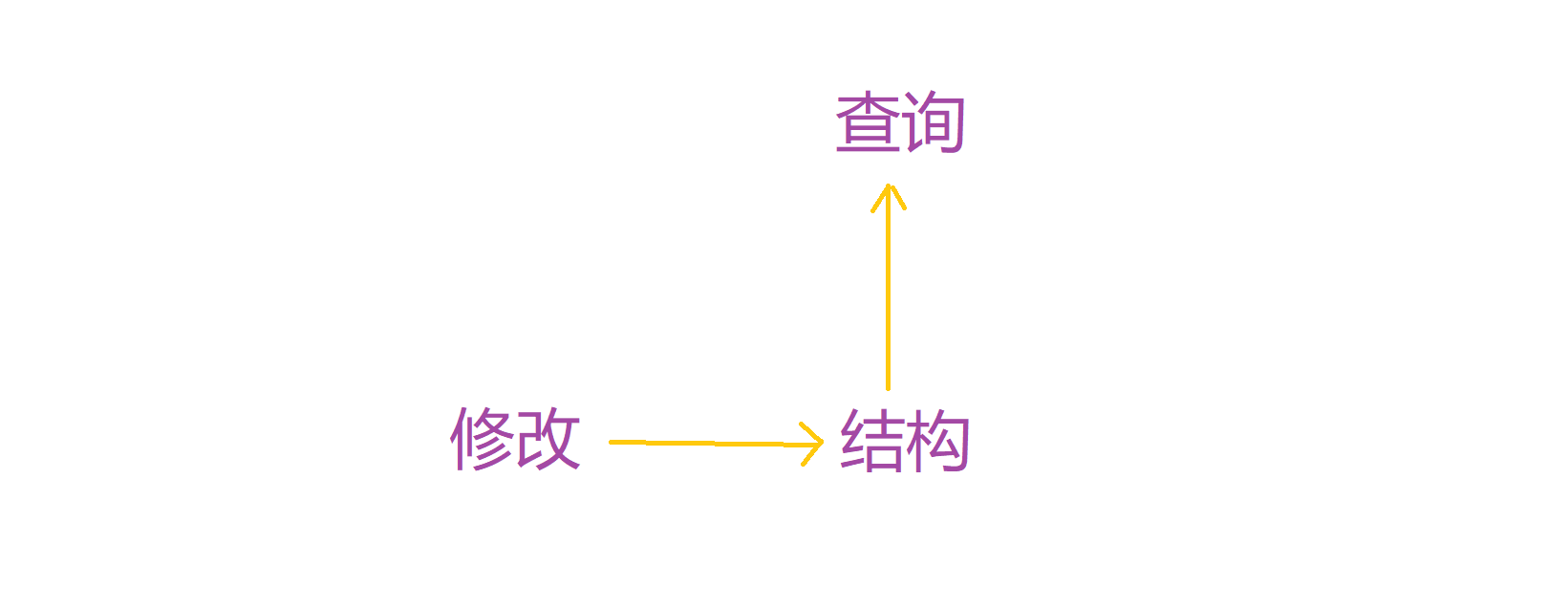
我们修改时是用一个结构也就是数据结构进行修改的维护，然后查询也只和结构里的内容有关。也就是说我如何如何修改与查询是没有直接关系的，千万不要把全部混在一起。把握这层关系可以更好地运用我们的数据结构。

最后希望你喜欢这篇BLOG！