杭州OI学习之旅Day1打卡——看似神奇实则平实的的左偏树。今天在陈学长的带领之下学习了堆和左偏树，这篇BLOG，就让我们一同走进左偏树吧。
【PS 参考资料 黄源河《左 偏 树 的 特 点 及 其 应 用》】

堆

左偏树的实质是一个可并堆，在了解可并堆之前我们需要先了解堆。

堆是什么？看起来很高级，但其实它就是利用完全二叉树的结构来维护一组数据，然后进行相关操作，一般的操作进行一次的时间复杂度在O(1)~O(logn)之间。

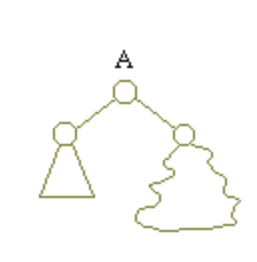
堆又一般分为大根堆和小根堆，大根堆顾名思义，就是对于每一个节点，他的值（也就是key值）比他的左右两个节点都要大。小根堆则刚好相反，对于每一个节点，他的值（也就是key值）比他的左右两个节点都要小。下面给出一个大根堆的例子：

可并堆

可并堆顾名思义，就是支持合并操作的堆，即可以实现在合并操作之后仍然保持之前堆的性质：

如果我们不需要合并操作，那么二叉堆就是最理想的选择，但是它的合并是O(n)的，这意味着它不适用于直接运用在合并堆的题目上。可并堆的种类多种多样，但在这篇BLOG，我们重点介绍的是左偏树。

左偏树

左偏树最早是黄源河在IOI2005国家集训队论文中提出的，下面我们就沿着它的思路一起学习左偏树吧。

左偏树的定义

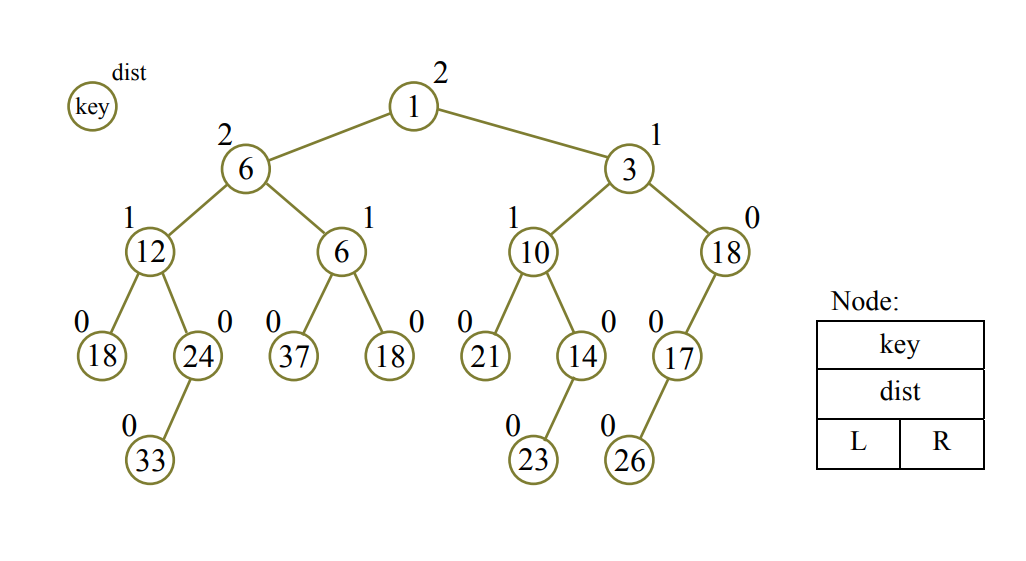
左偏树(Leftist Tree)是一种可并堆的实现。左偏树是一棵二叉树，它的节点除了和二叉树的节点一样具有左右子树指针( left, right )外，还有两个属性：键值(key)和距离(dist)。键值上面已经说过，是用于比较节点的大小。距离则是如下定义的：

节点 i 称为外节点(external node)，当且仅当节点 i 的左子树或右子树为空( left(i) = NULL 或 right(i) = NULL )；节点 i 的距离( dist( i ) )是节点 i 到它的后代中，最近的外节点所经过的边数。特别的，如果节点 i 本身是外节点，则它的距离为 0；而空节点的距离规定为-1 (dist(NULL) = -1)。

我们有时也会提到一棵左偏树的距离，这指的是该树根节点的距离。

左偏树的性质

[性质 1] 节点的键值小于或等于它的左右子节点的键值。

即 key(i)≥key(parent(i)) 这条性质又叫堆性质。符合该性质的树是堆有序的(Heap-Ordered)。有了性质 1，我们可以知道左偏树的根节点是整棵树的最小节点，于是我们可以在 O(1) 的时间内完成取最小节点操作。

[性质 2] 节点的左子节点的距离不小于右子节点的距离。

即 dist(left(i))≥dist(right(i)) 这条性质称为左偏性质。性质 2 是为了使我们可以以更小的代价在优先队列的其它两个基本操作（插入节点、删除最小节点）进行后维持堆性质。

这样做有什么意义呢？我们会发现，每次插入都是插入到该节点的右节点上。这时要满足性质2，就会让左节点比右节点更“大个”一点，这时我们插入到右节点时，就会让整个堆的左右较为平均，不会让左右子树过于膨胀。

这两条性质是对每一个节点而言的，因此可以简单地从中得出，左偏树的每个节点的左右子树都是左偏树。

由这两条性质，我们可以得出左偏树的定义：左偏树是具有左偏性质的堆有序二叉树。

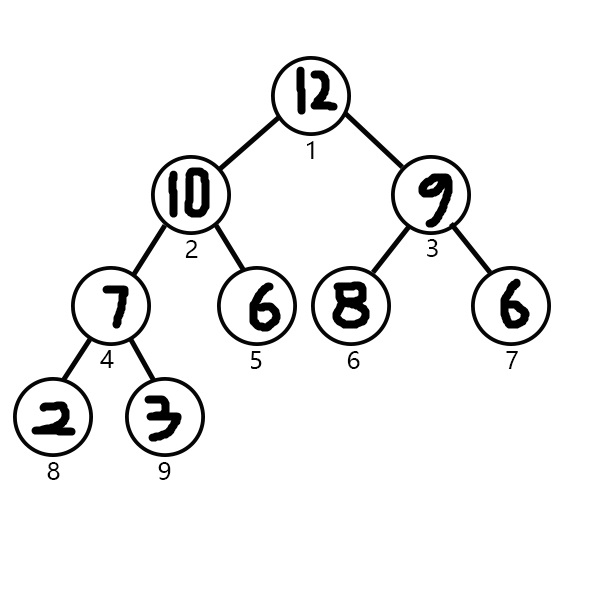
下面给出一棵左偏树：

[性质 3] 节点的距离等于它的右子节点的距离加 1。

即 dist( i ) = dist( right( i ) ) + 1 。由于性质二，对于任意节点i，它的右节点的距离一定小于等于它的左节点的距离，我们对于距离的定义又是到外节点的最小距离，所以dist( i ) = dist( right( i ) ) + 1 这个结论就很显然了。

特殊的，外节点的距离为 0。此时，由于性质 2，它的右子节点必为空节点。为了满足性质 3，故前面规定空节点的距离为-1。

我们的印象中，平衡树是具有非常小的深度的，这也意味着到达任何一个节点所经过的边数很少。左偏树并不是为了快速访问所有的节点而设计的，它的目的是快速访问最小节点以及在对树修改后快速的恢复堆性质。从图中我们可以看到它并不平衡，由于性质 2 的缘故，它的结构偏向左侧，不过距离的概念和树的深度并不同，左偏树并不意味着左子树的节点数或是深度一定大于右子树。

下面我们通过一些引理来讨论左偏树的距离和节点数的关系。

[引理 1] 若左偏树的距离为一定值，则节点数最少的左偏树是完全二叉树。

证明：由性质 2 可知，当且仅当对于一棵左偏树中的每个节点 i，都有dist(left(i)) = dist(right(i)) 时，该左偏树的节点数最少。显然具有这样性质的二叉树是完全二叉树。

[引理 2] 若一棵左偏树的距离为k，则这棵左偏树至少有 2k+1-1 个节点。

证明：由引理 1 可知，当这样的左偏树节点数最少的时候，是一棵完全二叉树。距离为k的完全二叉树高度也为k，节点数为 2^(k+1)-1，所以距离为k的左偏树至少有 2^(k+1)-1 个节点。

作为定理 1 的推论，我们有：

[性质 4] 一棵 N 个节点的左偏树距离最多为 ⎣log(N+1)⎦ -1

证明：设一棵N个节点的左偏树距离为k，由定理 1 可知，N ≥ 2k+1-1，因此k≤ ⎣log(N+1)⎦ -1。

有了上面的 4 个性质，我们可以开始讨论左偏树的操作了。

左偏树的操作

1.左偏树的合并

C ← Merge(A,B)

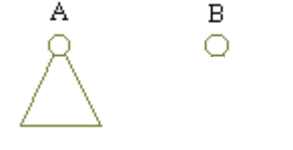
Merge( ) 把 A,B 两棵左偏树合并，返回一棵新的左偏树 C，包含 A 和 B 中的所有元素。在本文中，一棵左偏树用它的根节点的指针表示，如下图：

在合并操作中，最简单的情况是其中一棵树为空（也就是，该树根节点指针为 NULL）。这时我们只须要返回另一棵树。

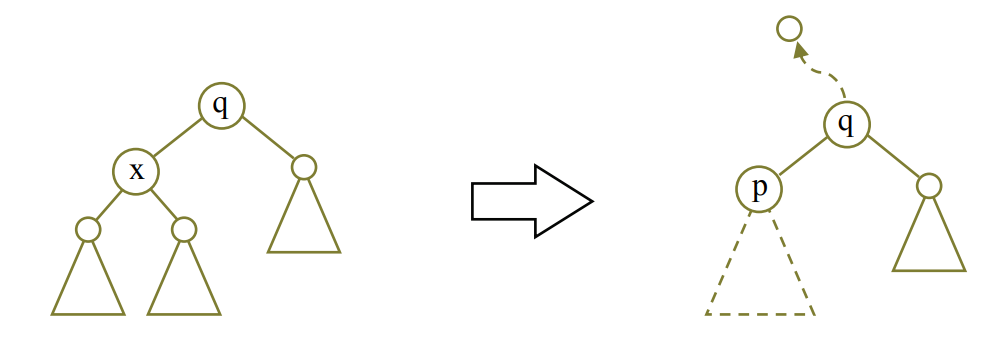
若 A 和 B 都非空，我们假设 A 的根节点小于等于 B 的根节点（否则交换A,B），把A的根节点作为新树C的根节点，剩下的事就是合并A的右子树right(A)和 B 了,即right(A) ← Merge(right(A), B)，如下图：

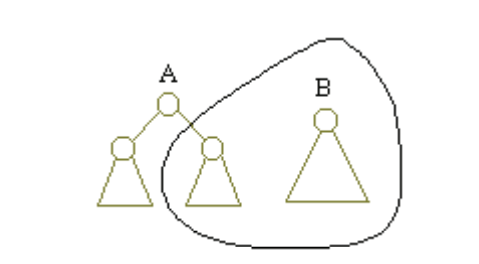
合并了 right(A) 和 B 之后，right(A) 的距离可能会变大，当 right(A) 的距离大于 left(A) 的距离时，左偏树的性质 2 会被破坏。在这种情况下，我们只须要
交换 left(A) 和 right(A)，即若 dist(left(A)) > dist(right(A))，交换 left(A) 和 right(A)。

最后，由于 right(A) 的距离可能发生改变，我们必须更新 A 的距离：dist(A) ← dist(right(A)) + 1

不难验证，经这样合并后的树 C 符合性质 1 和性质 2，因此是一棵左偏树。

至此左偏树的合并就完成了。

下面应用黄源河的一个栗子：

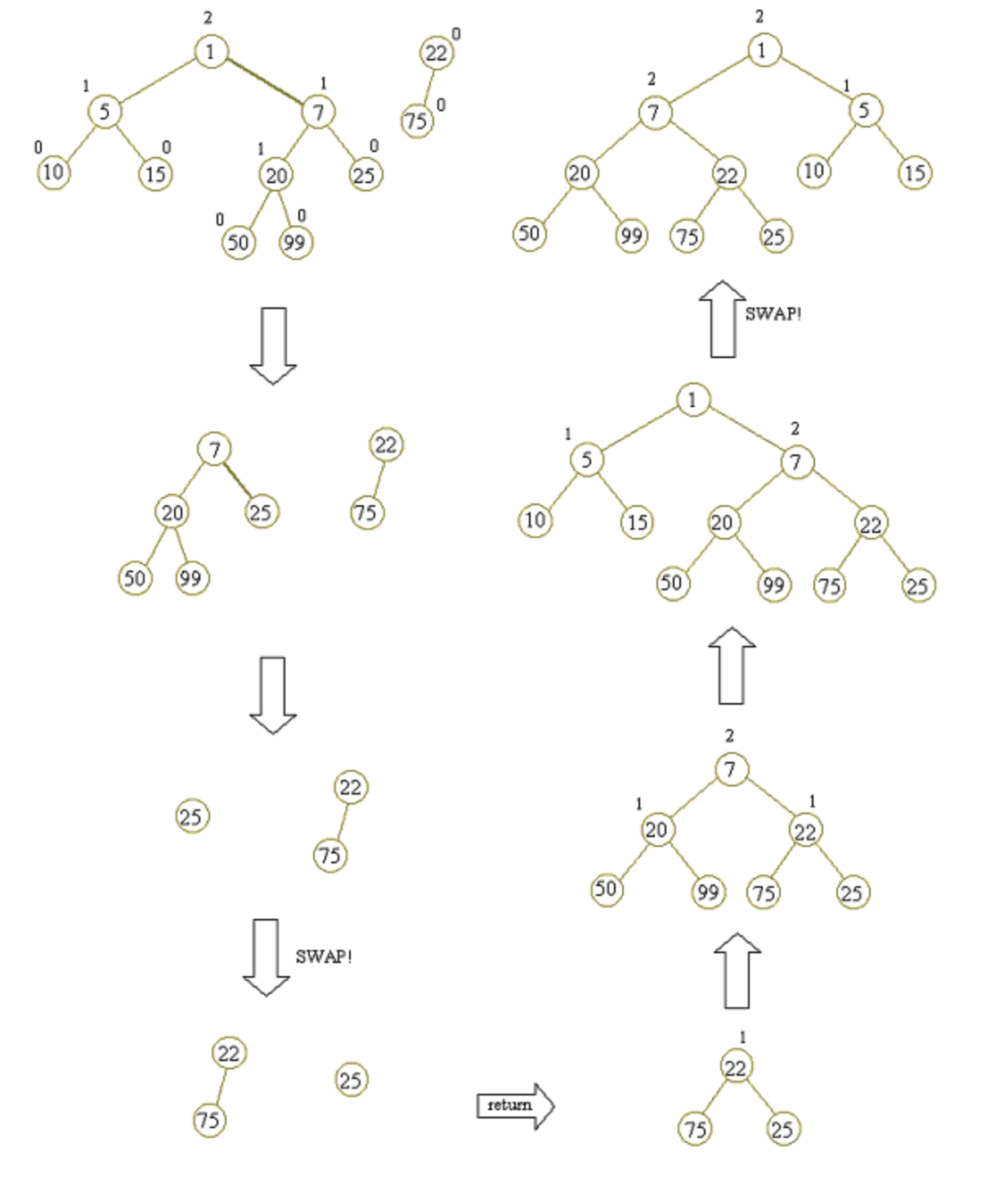
我们可以用下面的伪代码描述左偏树的合并过程：

Function Merge(A, B)
If A = NULL Then return B
If B = NULL Then return A
If key(B) < key(A) Then swap(A, B)
  right(A) ← Merge(right(A), B)
If dist(right(A)) > dist(left(A)) Then
 swap(left(A), right(A))
If right(A) = NULL Then dist(A) ← 0
Else dist(A) ← dist(right(A)) + 1
return A
End Function

我们令N1和N2分别为左偏树 A 和 B 的节点个数。因此合并操作最坏情况下的时间复杂度为
O( ⎣log(N1+1)⎦ + ⎣log(N2+1)⎦ -2) = O(log N1 + log N2)。

2.插入新节点

单节点的树一定是左偏树，因此向左偏树插入一个节点可以看作是对两棵左偏树的合并。下面是插入新节点的代码：

Procedure Insert(x, A)
 B ← MakeIntoTree(x)
 A ← Merge(A, B)
End Procedure

由于合并的其中一棵树只有一个节点，因此插入新节点操作的时间复杂度是O(logn)。

3.删除最小节点

由性质 1，我们知道，左偏树的根节点是最小节点。在删除根节点后，剩下的两棵子树都是左偏树，需要把他们合并。删除最小节点操作的代码也非常简单：

Function DeleteMin(A)
 t ← key(root(A))
 A ← Merge(left(A), right(A))
return t
End Function

由于删除最小节点后只需进行一次合并，因此删除最小节点的时间复杂度也为 O(logn)。

4.左偏树的构造

将 n 个节点构建成一棵左偏树，这也是一个常用的操作。

算法一 暴力算法——逐个节点插入，时间复杂度为 O(n log n)。
算法二 仿照二叉堆的构建算法，我们可以得到下面这种算法：

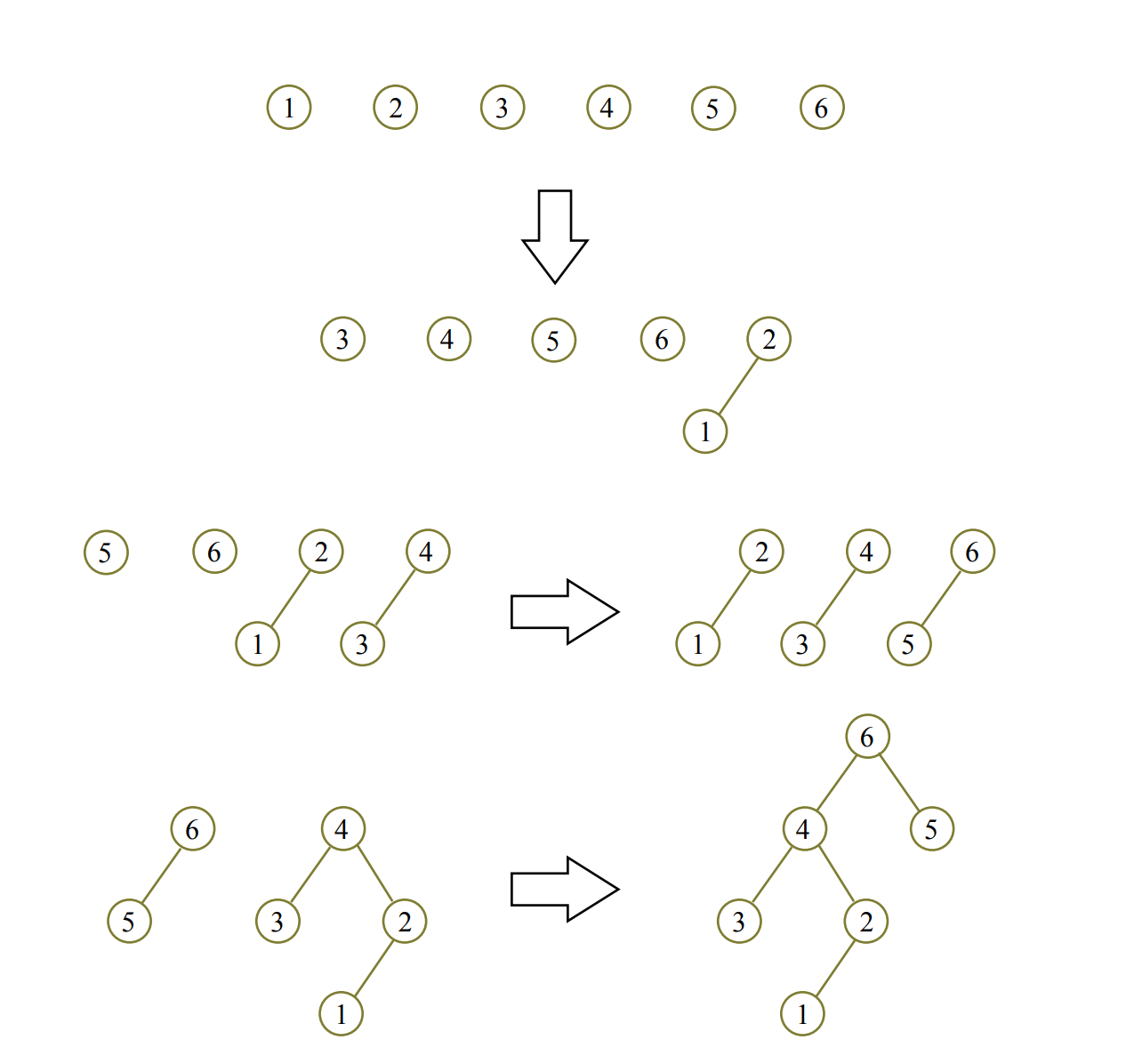
1.将 n 个节点（每个节点作为一棵左偏树）放入先进先出队列。
2.不断地从队首取出两棵左偏树，将它们合并之后加入队尾。
3.当队列中只剩下一棵左偏树时，算法结束。

5.删除任意已知节点

已知在这里不是指知道要删除的点的值是多少，而是知道这个数在序列或树中的位置。

上面已经提过，在删除一个节点以后，将会剩下它的两棵子树，它们都是左偏树，我们先把被删除节点 x 的左右子树并成一棵新的左偏树。

p ← Merge(left(x), right(x))

现在 p 指向了这颗新的左偏树，如果我们删除的是根节点，此时任务已经完成了。不过，如果被删除节点 x 不是根节点就有点麻烦了。

这时 p 指向的新树的距离有可能比原来 x 的距离要大或小，这势必有可能影响原来 x 的父节点 q 的距离，因为 q 现在成为新树 p 的父节点了。于是就要仿照合并操作里面的做法，对q 的左右子树作出调整，并更新 q 的距离。这一过程引起了连锁反应，我们要顺着 q 的父节点链一直往上进行调整。

新树 p 的距离为 dist(p)，如果 dist(p)+1 等于 q 的原有距离 dist(q)，那么不管p 是 q 的左子树还是右子树，我们都不需要对 q 进行任何调整，此时删除操作也
就完成了。

如果 dist(p)+1 小于 q 的原有距离 dist(q)，那么 q 的距离必须调整为 dist(p)+1，而且如果 p 是左子树的话，说明 q 的左子树距离比右子树小，必须交换子树。由
于 q 的距离减少了，所以 q 的父节点也要做出同样的处理。

剩下就是另外一种情况了，那就是 p 的距离增大了，使得 dist(p)+1 大于 q的原有距离 dist(q)。在这种情况下，如果 p 是左子树，那么 q 的距离不会改变，此时删除操作也可以结束了。如果 p 是右子树，这时有两种可能：一种是 p 的距离仍小于等于 q 的左子树距离，这时我们直接调整 q 的距离就行了；另一种是 p的距离大于 q 的左子树距离，这时我们需要交换 q 的左右子树并调整 q 的距离，交换完了以后 q 的右子树是原来的左子树，由于之前讲到的性质2，它的距离会≥修改前右子树的距离，故它的距离加 1 只能等于或大于 q 的原有距离，如果等于成立，删除操作可以结束了，否则 q 的距离将增大，我们还要对 q 的父节点做出相同的处理。

删除任意已知节点操作的代码如下：

Procedure Delete(x)
 q ← parent(x)
 p ← Merge(left(x), right(x))
 parent(p) ← q
If q ≠ NULL and left(q) = x Then
 left(q) ← p
If q ≠ NULL and right(q) = x Then
 right(q) ← p
While q ≠ NULL Do
 If dist(left(q)) < dist(right(q)) Then
 swap(left(q), right(q))
 If dist(right(q))+1 = dist(q) Then
 Exit Procedure
 dist(q) ← dist(right(q))+1
 p ← q
 q ← parent(q)
End While
End Procedure 

所以总的实现方法就很显然了。

经典例题

左偏树的大致思路大家都已经明白了，下面我们就用两道经典例题带大家巩固一下左偏树吧。

【luogu p3377】【模板】左偏树（可并堆）

题目描述
如题，一开始有N个小根堆，每个堆包含且仅包含一个数。接下来需要支持两种操作：

操作1： 1 x y 将第x个数和第y个数所在的小根堆合并（若第x或第y个数已经被删除或第x和第y个数在用一个堆内，则无视此操作）

操作2： 2 x 输出第x个数所在的堆最小数，并将其删除（若第x个数已经被删除，则输出-1并无视删除操作）

输入输出格式
输入格式：
第一行包含两个正整数N、M，分别表示一开始小根堆的个数和接下来操作的个数。

第二行包含N个正整数，其中第i个正整数表示第i个小根堆初始时包含且仅包含的数。

接下来M行每行2个或3个正整数，表示一条操作，格式如下：

操作1 ： 1 x y

操作2 ： 2 x

输出格式：
输出包含若干行整数，分别依次对应每一个操作2所得的结果。

输入输出样例
输入样例#1：
5 5
1 5 4 2 3
1 1 5
1 2 5
2 2
1 4 2
2 2
输出样例#1：
1
2
说明
当堆里有多个最小值时，优先删除原序列的靠前的，否则会影响后续操作1导致WA。

时空限制：1000ms,128M

数据规模：
对于30%的数据：N<=10，M<=10
对于70%的数据：N<=1000，M<=1000
对于100%的数据：N<=100000，M<=100000

这道题很明显是要我们实现一个可以合并的小根堆，这很明显就是一道左偏树的裸题了，下面就给出这道题也是简单的左偏树的模板：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
struct node
{
    int l,r,key,dist,f;
    void init()
    {
        l=0;r=0;f=0;
        key=0;dist=-1;
    }
}tr[110000];

int i,j,k,m,n,o,p,js,jl,jk,x,y,z;

void change(int &x,int &y)
{
    int z=x;x=y;y=z;
}

int find(int x)
{
    while(tr[x].f!=0)x=tr[x].f;
    return(x);
}

int merge(int a,int b)
{
    if(tr[a].dist==-1)return(b);
    if(tr[b].dist==-1)return(a); 
    if((tr[b].key<tr[a].key)||(tr[b].key==tr[a].key && b<a))change(a,b);
    tr[a].r=merge(tr[a].r,b);

    tr[tr[a].r].f=a;
    if(tr[tr[a].r].dist>tr[tr[a].l].dist)change(tr[a].r,tr[a].l);
    if(tr[tr[a].r].dist==-1)tr[a].dist=0;
    else tr[a].dist=tr[tr[a].r].dist+1;
    return(a);
}

int main()
{
    scanf("%d%d",&n,&m);
    tr[0].init();
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&x);
        tr[i].key=x;
        tr[i].dist=0;
    }

    for(int i=1;i<=m;i++)
    {
        scanf("%d",&o);
        if(o==1)
        {
            scanf("%d%d",&x,&y);
            if(tr[x].dist!=-1 && tr[y].dist!=-1)
            {
                x=find(x);
                y=find(y);
                if(x!=y)merge(x,y);
            }
        } 
        else
        {
            scanf("%d",&x);
            if(tr[x].dist==-1)printf("-1\n");
            else
            {
                x=find(x);
                printf("%d\n",tr[x].key);
                tr[x].dist=-1;

                tr[tr[x].l].f=0;tr[tr[x].r].f=0;
                merge(tr[x].l,tr[x].r);
            }
        }
    }
    return 0;
}

【luogu P1456】Monkey King

题目描述:
Once in a forest, there lived N aggressive monkeys. At the beginning, they each does things in its own way and none of them knows each other. But monkeys can't avoid quarrelling, and it only happens between two monkeys who does not know each other. And when it happens, both the two monkeys will invite the strongest friend of them, and duel. Of course, after the duel, the two monkeys and all of there friends knows each other, and the quarrel above will no longer happens between these monkeys even if they have ever conflicted.

Assume that every money has a strongness value, which will be reduced to only half of the original after a duel(that is, 10 will be reduced to 5 and 5 will be reduced to 2).

And we also assume that every monkey knows himself. That is, when he is the strongest one in all of his friends, he himself will go to duel.

一开始有n只孤独的猴子，然后他们要打m次架，每次打架呢，都会拉上自己朋友最牛叉的出来跟别人打，打完之后战斗力就会减半，每次打完架就会成为朋友（正所谓不打不相识o(∩_∩)o ）。问每次打完架之后那俩猴子最牛叉的朋友战斗力还有多少，若朋友打架就输出-1.

输入输出格式
输入格式：
There are several test cases, and each case consists of two parts.

First part: The first line contains an integer N(N<=100,000), which indicates the number of monkeys. And then N lines follows. There is one number on each line, indicating the strongness value of ith monkey(<=32768).

Second part: The first line contains an integer M(M<=100,000), which indicates there are M conflicts happened. And then M lines follows, each line of which contains two integers x and y, indicating that there is a conflict between the Xth monkey and Yth.

有多组数据

输出格式：
For each of the conflict, output -1 if the two monkeys know each other, otherwise output the strength value of the strongest monkey among all of its friends after the duel.

输入输出样例
输入样例#1：
5
20
16
10
10
4
5
2 3
3 4
3 5
4 5
1 5
输出样例#1：
8
5
5
-1
10

这题也非常的明显。每次猴子打架都要找最强壮的朋友——支持查找最大值；打完成为朋友——支持合并。很明显这就是一个大根堆的左偏树。

接下来剩下的问题就是处理打完战斗力减半了，这也很好实现，每次打完以后，对于打架双方的左偏树x，y，都分别将根节点去出，key值除以2，然后先将它的左右儿子先合并为一棵左偏树，然后再把根节点用插入节点的方法分别插回各自的左偏树。最后将两棵左偏树合并，输出根节点就行了。

注意有多组数据！！！

下面给出代码：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
struct node
{
    int l,r,key,dist,f;
    void init()
    {
        l=0;r=0;f=0;
        key=0;dist=-1;
    }
}tr[110000];

int i,j,k,m,n,o,p,js,jl,jk,x,y,z,xx,yy,zz,newx,newy;

void change(int &x,int &y)
{
    int z=x;x=y;y=z;
}

int find(int x)
{
    while(tr[x].f!=0)x=tr[x].f;
    return(x);
}

int merge(int a,int b)
{
    if(tr[a].dist==-1)return(b);
    if(tr[b].dist==-1)return(a); 
    if(tr[b].key>tr[a].key)change(a,b);
    tr[a].r=merge(tr[a].r,b);

    tr[tr[a].r].f=a;
    if(tr[tr[a].r].dist>tr[tr[a].l].dist)change(tr[a].r,tr[a].l);
    if(tr[tr[a].r].dist==-1)tr[a].dist=0;
    else tr[a].dist=tr[tr[a].r].dist+1;
    return(a);
}

int main()
{
    while(scanf("%d",&n)!=EOF)
    {

    tr[0].init();
    for(int i=1;i<=n;i++)
    {
        tr[i].init();
        scanf("%d",&x);
        tr[i].key=x;
        tr[i].dist=0;
    }

    scanf("%d",&m);

    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&x,&y);

        x=find(x);y=find(y);

        if(x==y)printf("-1\n");
        else
        {
            tr[x].key=tr[x].key/2;
            tr[y].key=tr[y].key/2;

            tr[tr[x].l].f=0;tr[tr[x].r].f=0;
            tr[tr[y].l].f=0;tr[tr[y].r].f=0;

            xx=merge(tr[x].l,tr[x].r);
            tr[x].l=0;tr[x].r=0;tr[x].dist=0;
            newx=merge(xx,x);

            yy=merge(tr[y].l,tr[y].r);
            tr[y].l=0;tr[y].r=0;tr[y].dist=0;
            newy=merge(yy,y);

            zz=merge(newx,newy);

            printf("%d\n",tr[zz].key);
        }
    }
    }
    return 0;
}

结语

这段时间应该是学习高级数据结构的了，左偏树是学习堆不可缺少的知识点，希望你能通过这篇BLOG彻底掌握左偏树。其实左偏树作为可合并堆的一种，不会考的很难拿的，毕竟它归根到底只是一个堆，堆能考到多难，它就能考到多难。希望你喜欢这篇BLOG！