最近有些高产啊……咳咳咳……今天看到了一个非常实用的计算几何定理,决定带上简单易懂的证明分享给大家QwQ
什么是Pick定理
皮克定理是指一个计算点阵中顶点在格点上的多边形面积公式,该公式可以表示为2S=2a+b-2,其中a表示多边形内部的点数,b表示多边形边界上的点数,S表示多边形的面积。
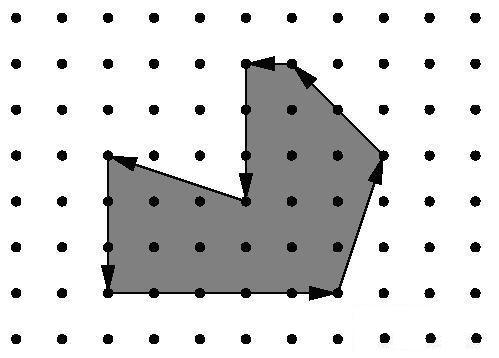
这个算法最早是由奥地利的的George Alexander Pick提出,为了纪念他,所以这个定理称为pick定理。
Pick定理定义
一张方格纸上,上面画着纵横两组平行线,相邻平行线之间的距离都相等,这样两组平行线的交点,就是所谓格点。如果取一个格点做原点O,如图1,取通过这个格点的横向和纵向两直线分别做横坐标轴OX和纵坐标轴OY,并取原来方格边长做单位长,建立一个坐标系。这时前面所说的格点,显然就是纵横两坐标都是整数的那些点。如图1中的O、P、Q、M、N都是格点。由于这个缘故,我们又叫格点为整点。
一个多边形的顶点如果全是格点,这多边形就叫做格点多边形。有趣的是,这种格点多边形的面积计算起来很方便,只要数一下图形边线上的点的数目及图内的点的数目,就可用公式算出。
这个公式是皮克(Pick)在1899年给出的,被称为“皮克定理”,这是一个实用而有趣的定理。
给定顶点坐标均是整点(或正方形格点)的简单多边形,皮克定理说明了其面积S和内部格点数目n、边上格点数目s的关系:
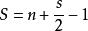
(其中n表示多边形内部的点数,s表示多边形边界上的点数,S表示多边形的面积)
我们运用百度百科上的一个栗子!
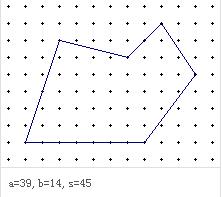
小学生都看得懂的证明
在网上你可以看到各种证明Pick定理的方法,但是我觉得下面介绍的这种方法,是真的小学生都看得懂的证明方法:
在这个证明之前,我们需用到一个很浅显的预备知识:“多边形外角和等于一个周角”。
以下图的格点多边形ABCDE为例,其边界上有a个格点,内部有b个格点。
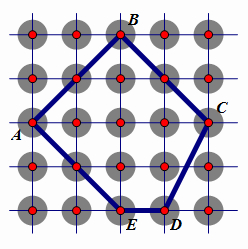
设想在平面的每个格点放一个铁饼,满足:
(1)每个铁饼都一样大的圆(或者说是圆柱),圆心是格点;
(2)每个铁饼都恰好重1克;
(3)每个铁饼的半径都做得尽量小——不仅铁饼之间互相不重叠,而且还使得多边形ABCDE内部的每个格点上所放的铁饼,都完全落在该多边形的内部;多边形ABCDE外部的每个格点上所放的铁饼,都完全落在该多边形的外部。
首先,考虑多边形ABCDE的边界以内的铁的总重。
这可以分如下两类进行计算:
第一类:其内部格点上放的铁饼.此类总重显然是b克。
第二类:其边界格点上放的铁饼落在边界以内的铁.假设每个边界格点上放的铁饼,恰有一半落在边界以内,则总重为a/2克.但显然在每个顶点处放的铁饼,落在边界以内的铁实际不足一半,比一半还少该顶点的一个外角内所含的铁,然后我们知道多边形的外角和为360°,所以所有这种外角内所含的铁恰好拼成一块完整的铁饼(因为多边形外角和等于一个周角).所以后一类铁的总重是a/2-1克。
因而,多边形ABCDE的边界以内的铁的总重是a/2+b-1克.
接下来,设想将平面上所有铁饼全部熔化,打造成一张厚薄均匀的铁板盖在整个平面上.这可以看作是:将每个单位正方形的四个顶点处的每个90°的扇形铁饼,熔化在这个正方形内部,故熔化后每个单位正方形内的铁都是1克.进而,平面上任意图形,其面积是多少,其内部就含多少克铁。
因而,熔化并重新打造后,多边形ABCDE的边界以内的铁的总重是S克。
最后,注意到这个熔化并重新打造的过程,可以看成是:每个格点处的铁饼中的铁,按(以该格点为中心)放射状的方式重新适当改动位置而已.这样的改动,不会使格点多边形ABCDE外面的铁跑到多边形内部,也不会使内部的铁跑到外部。
即熔化并重新打造的前后,多边形ABCDE的边界以内的铁的总重是不变的,所以S=a/2+b-1。
特别感谢思路提供者Orz大佬!
结语
目前我还没找到试用的OI题目,但我相信在不久的未来一定能运用到这个定理的题目!希望你喜欢这篇BLOG!
jvruomeiding
wow
我想学你