AC自动机补档第二期……不懂KMP的同学可以好好学习一下这个神奇的单字符串匹配问题的算法吧！

字符串匹配

什么叫字符串匹配呢？假设我们有一个主字符串和一个子串：

主串：abcbcglx
子串：bcgl

那么在主字符串中，有没有包含子串呢？当然，你一眼就看出，从主串的第4位到第7位恰好为子串 bcgl；这时我们的匹配算法就返回 4 也就是子串在主串中第一次出现的起始位置；若匹配失败，既主串中没有包含子串，则会返回error之类的信息。

这就是字符串的匹配。

会TLE的暴力算法

那么通常，人们是如何解决这类字符串匹配的问题的呢？很简单，暴力都能解决问题。

我们先对主串和子串进行编号

a b c b c g l x
1 2 3 4 5 6 7 8

b c g l
1 2 3 4

然后枚举主串中的每个位置为子串的起始位置，然后判断是否匹配。

但是这种算法的复杂度是O(nm)【n，m分别为主串和子串的长度】，在大范围的题目是肯定会超时的，所以我们就要推出今天的主角——KMP算法！

什么是KMP算法

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt同时发现，因此人们称它为克努特——莫里斯——普拉特操作（简称KMP算法），也通常被叫做看毛片算法，时间复杂度控制在了 O（m+n）。

那么这种神奇的算法是如何运作的呢？

我们先来举一个例子：
我们首先有一个主串和一个子串：

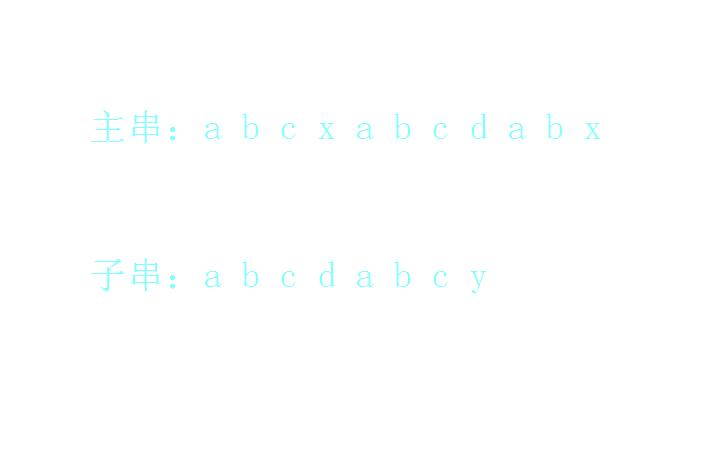
我们开始逐位比较，首先a和a匹配上了：

b和b匹配上了：

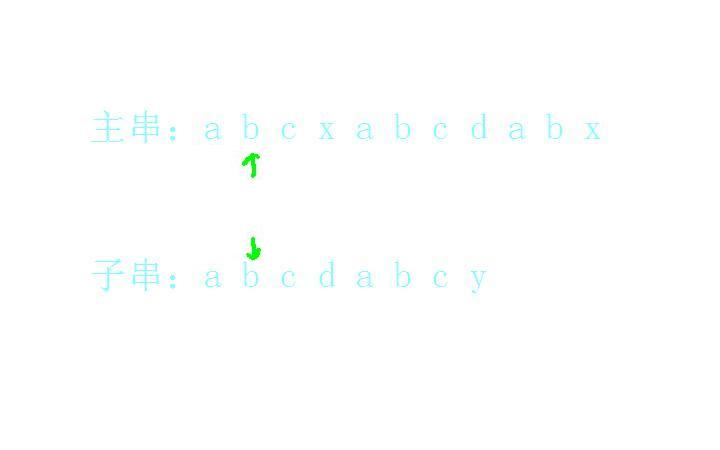
c和c匹配上了：

x和d不匹配：

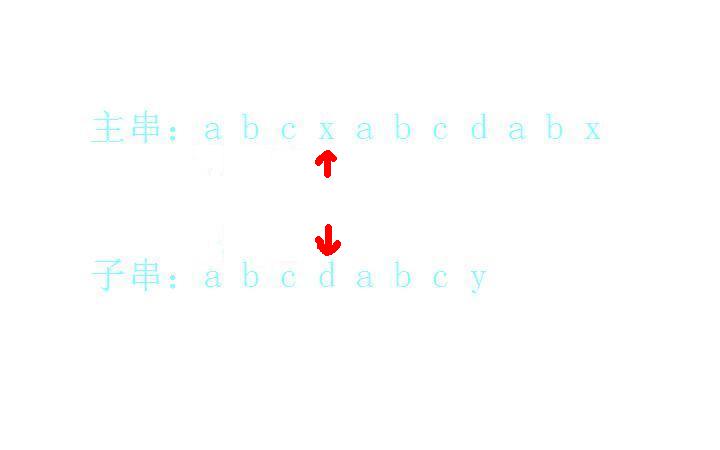
这时没办法，只好重新开始寻找开头，b和a无法匹配：

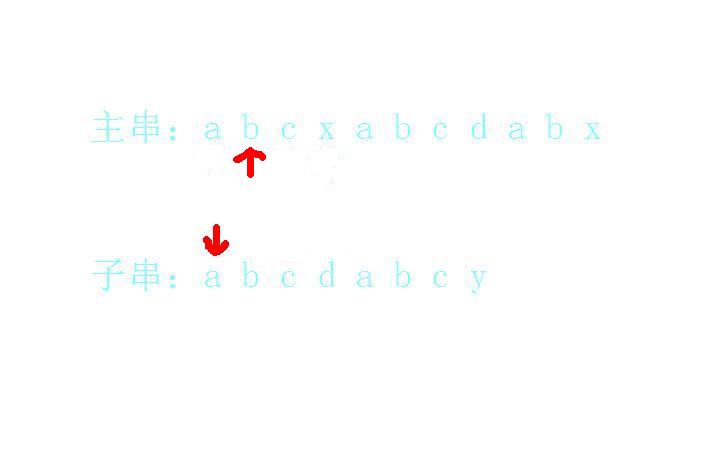
主串指针往后移，c和a无法匹配：

主串指针往后移，x和a无法匹配：

主串指针往后移，a和a终于匹配：

接着b和b匹配上了；

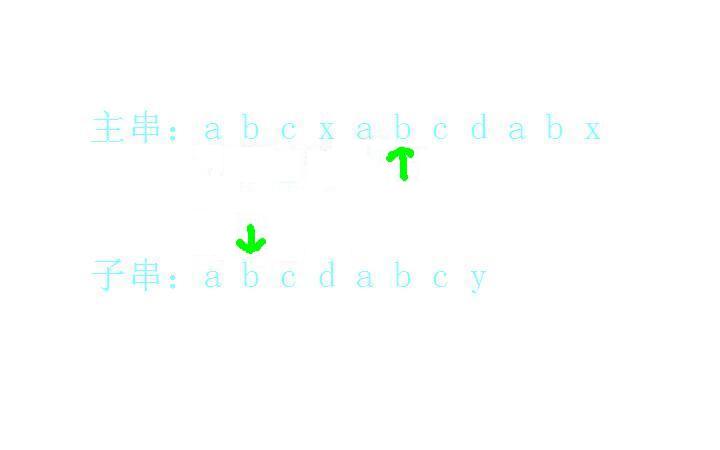
c和c匹配上了：

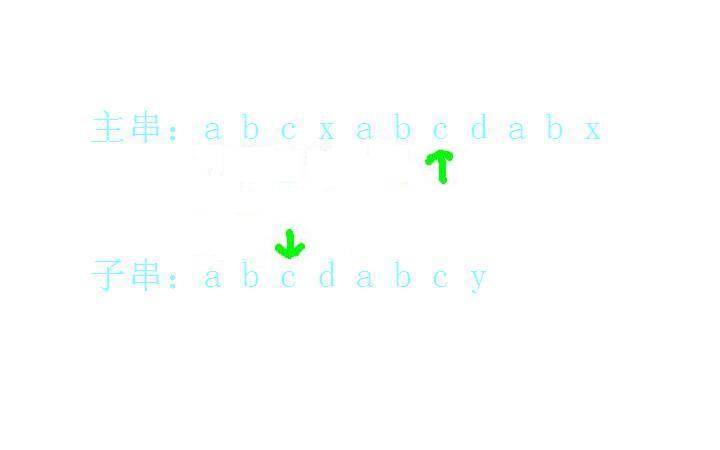
d和d匹配上了：

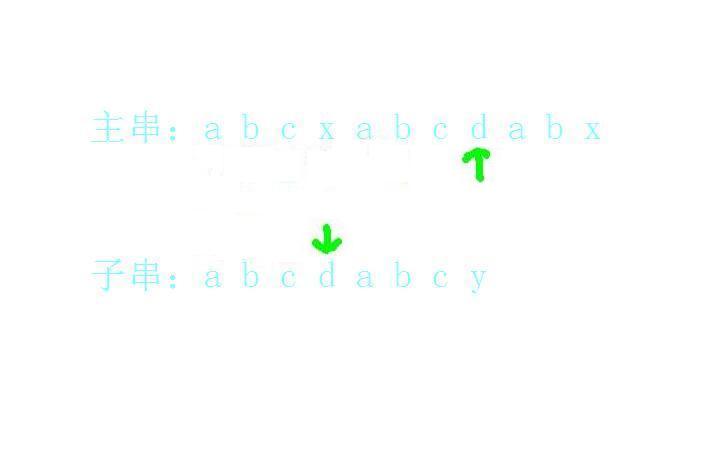
a和a匹配上了：

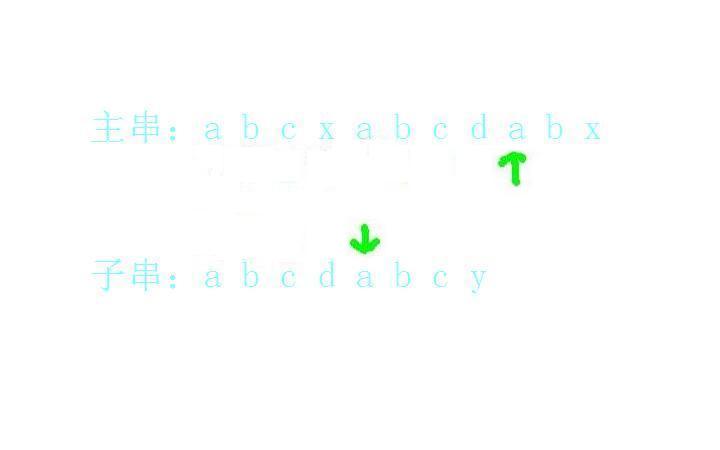
b和b匹配上了：

但是x和y无法匹配，匹配终止：

这时按暴力来想，子串只好前功尽弃，从头开始匹配；

但是细心的同学发现：

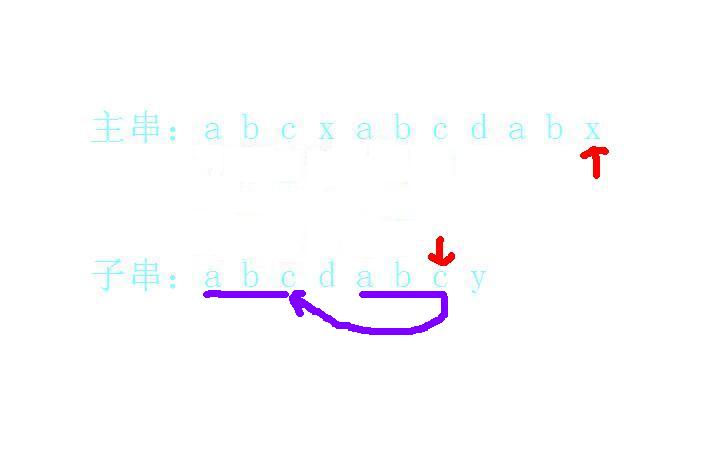
我们观察一下匹配失败的c的字符串：abcdab；
他的前缀是ab，他的后缀也是ab！

这有什么用呢？我们是在子串的abcdabc的末尾c这里匹配失败的，但是c前面我们已经正确匹配了ab，也就是说我们可以匹配一个ab开头的字符串的前两位，而子串恰好满足！

那么这个x可能是直接匹配前面这个ab后面的字符的，所以我们就在下一次的匹配时，直接跳过之前那个ab，从ab的后一个字符位置开始继续往后匹配就好了！

这就是KMP算法的精髓所在！

如何实现KMP

我们这里分为两块来实现KMP：

构造p数组

我们先要在子串上构造p数组，也就是我们上文跳来跳去的那个东西:

p[1]=0;
for(int i=2;i<=lenb;i++)
        {
            j=p[i-1];
            while(j>0 && sb[i]!=sb[j+1]) j=p[j];

            if(sb[i]==sb[j+1])p[i]=j+1;else p[i]=0;
        }

p数组的含义就是一个固定字符串的最长前缀和最长后缀相同的长度。

我们举个栗子！
比如：abcjkdabc，那么这个数组的最长前缀和最长后缀相同必然是abc。
cbcbc，最长前缀和最长后缀相同是cbc。
abcbc，最长前缀和最长后缀相同是不存在的。

而我们在这里求解的p【i】，是说以第一个字符开始，到第i个字符的字符串的最长前缀和最长后缀相同的长度。

所以对于目标子字符串，ababaca，长度是7，所以p[1]，p[2]，p[3]，p[4]，p[5]，p[6]，p[7]分别计算的是
a，ab，aba，abab，ababa，ababac，ababaca的相同的最长前缀和最长后缀的长度。由于a，ab，aba，abab，ababa，ababac，ababaca的相同的最长前缀和最长后缀是“”，“”，“a”，“ab”，“aba”，“”，“a”,所以p数组的值是[0,0,1,2,3,0,1]，这里0表示不存在，1表示存在长度为1，2表示存在长度为2。这是为了和代码相对应。

在主串上进行匹配

一样的按照之前讲的原理，我们类似的进行匹配就好啦！当第子串i个字符匹配失败的时候，我们就去看p【i】+1是否匹配，若不匹配，再继续看p【p【i】】+1能否匹配，以此类推，程序如下：

        int st,ed;
        j=0;
        for(int i=1;i<=lena;i++)
        {
            while(j>0 && sa[i]!=sb[j+1])j=p[j];
            if(sa[i]==sb[j+1])j++;
            if(j==lenb)
            {
                ed=i;
                st=i-lenb+1;
                break;
            }
        }

模板题

【caioj 1177】子串是否出现
题目描述
【题意】
有两个字符串SA和SB，SA是母串，SB是子串，问子串SB是否在母串SA中出现过。
如果出现过输出第一次出现的起始位置和结束位置，否则输出"NO"
【输入文件】
第一行SA（1 <= 长度 <= 100 0000）
第二行SB（1 <= 长度 <= 1000）
【输出文件】
如果SB在SA中出现过输出第一次出现的起始位置和结束位置，否则输出"NO"
【样例1输入】
aaaaabaa
aab
【样例1输出】
4 6
【样例2输入】
aaaaabaa
aax
【样例2输出】
NO

就是一道裸题，直接献上模板：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
char sa[1110000],sb[1100];
int p[1100];
int main()
{
    int lena,lenb,i,j;
    scanf("%s",sa+1);lena=strlen(sa+1);
    scanf("%s",sb+1);lenb=strlen(sb+1); 
    p[1]=0;
    for(int i=2;i<=lenb;i++)
    {
        j=p[i-1];
        while(j>0 && sb[i]!=sb[j+1]) j=p[j];

        if(sb[i]==sb[j+1])p[i]=j+1;else p[i]=0;
    }
    int st,ed;
    j=0;
    for(int i=1;i<=lena;i++)
    {
        while(j>0 && sa[i]!=sb[j+1])j=p[j];
        if(sa[i]==sb[j+1])j++;
        if(j==lenb)
        {
            ed=i;
            st=i-lenb+1;
            break;
        }
    }
    if(j==lenb) printf("%d %d\n",st,ed);
    else printf("NO\n");
    return 0; 
} 

结语

讲完这篇BLOG后，我们字符串的常见处理方法就到这里结束了！以后遇到什么新的算法再补充吧！希望你喜欢这篇BLOG！