在写完AC自动机后,就有小伙伴要求我具体讲解一下KMP和Trie树,那么这篇BLOG,就带你走进其实很简单的Trie树吧!
什么是字典树
基本概念
字典树,又称为单词查找树或Tire树,是一种树形结构,它是一种哈希树的变种,用于存储字符串及其相关信息。
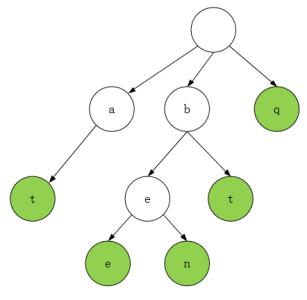
基本性质
1.根节点不包含字符,除根节点外的每一个子节点都包含一个字符
2.从根节点到某一节点。从根节点到该节点路径上经过的字符连接起来,就是该节点对应的字符串
3.同一个节点的所有子节点包含的字符都不相同
运用方面
典型应用是用于统计,排序和保存大量的字符串(不仅限于字符串),经常被搜索引擎系统用于文本词频统计。
优点缺点
字典树是经典的空间换时间的数据结构,利用字符串的公共前缀来减少查询时间,最大限度的减少无谓的字符串比较,查询效率据说比哈希树高。
但缺点就很显然了,就是空间比较大……
举个栗子
什么不太了解,没事,让我们来结合栗子来分析一下!
我们首先读入四个字符串
ba
b
band
abc
在没有读入前,我们有一个空空的根节点;

接着我们插入单词ba;
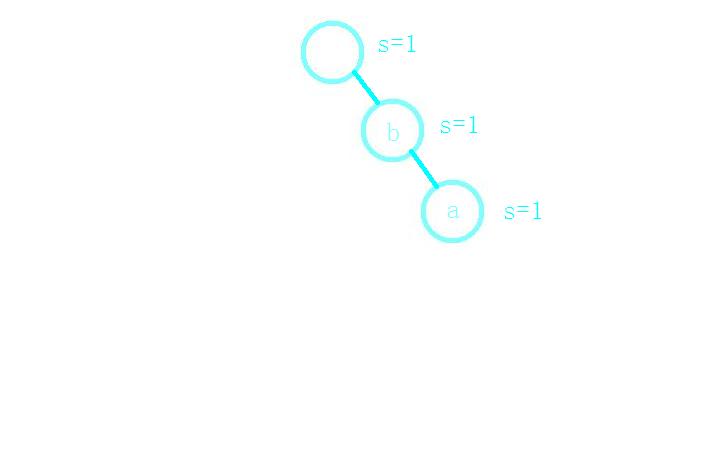
接着插入单词b,由于根节点有连向b的子节点,所以只需路径上的s++就好了;
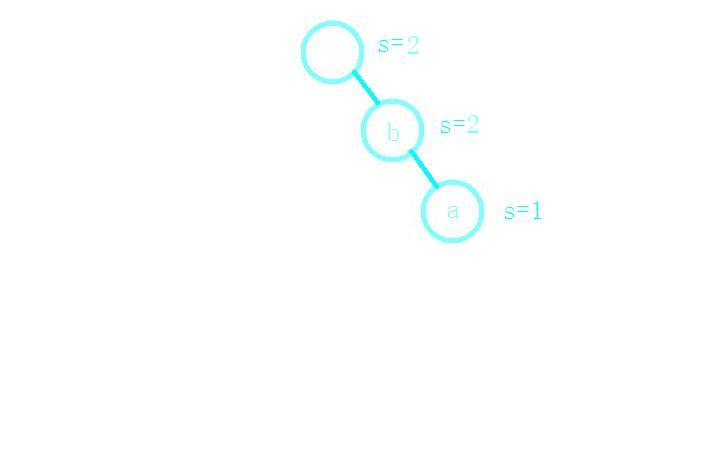
接着插入单词bank,ba之前就有,只需s++,而nk需要在ba后添加子节点完成存储;
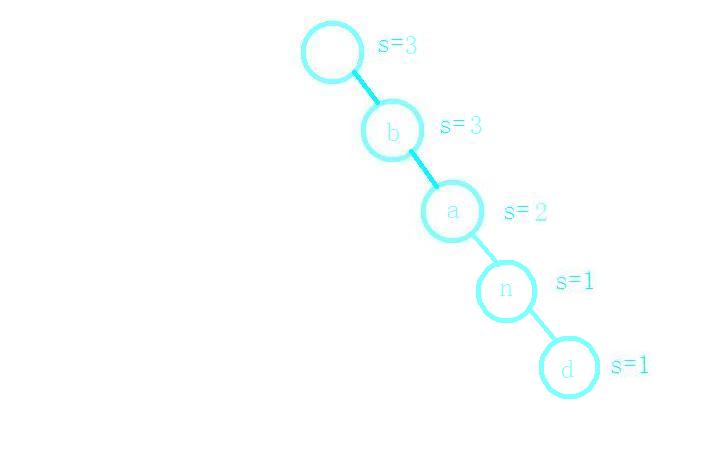
最后插入单词abc;
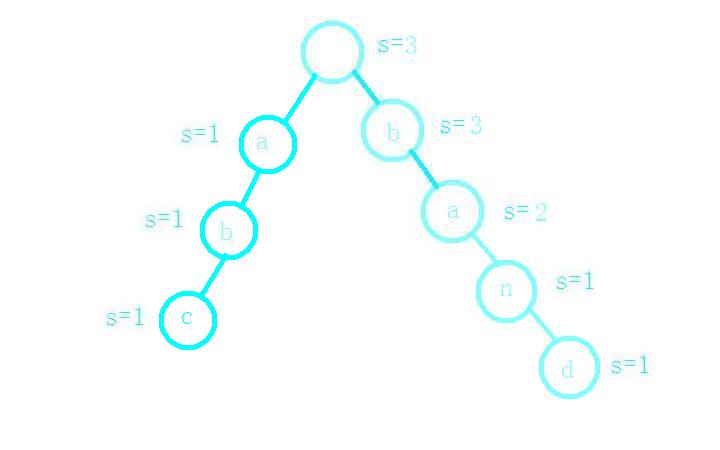
如何构造字典树
我们来结合程序一步一步来构造这棵可爱的字典树吧!!
构造节点
我们需要运用struct来存储字典树上每个节点的信息:
struct node
{
int s,v[27],val;
node()
{
s=0;
memset(v,-1,sizeof(v));
}
}t[410000];s是用来存储有多少个单词进过了这个节点,v是用来存储这个点从a到z的儿子节点分别在哪,而val则是存储这个节点的权值,至于权值代表什么,就要依照题目灵活变换了。
构造字典树
我们先抛出程序:
int bt(int root)
{
int len=strlen(a+1);int x=root;
for(int i=1;i<=len;i++)
{
int y=a[i]-'a'+1;//将a^z转化为1^26
if(t[x].v[y]==-1)t[x].v[y]=++tot;
x=t[x].v[y];t[x].s++;
}
}首先我们先读入了一个字符串a,它的长度为len;
接着我们对于它的字符进行循环处理,当我们处理到这个字符串的第i个字符的时候,我们要进行分类讨论——
我们用x存储第i-1个字符在字典树中的位置;
当我的前一个字符没有指向我的字符的时候,我就tot++,在字典树中开创一个新的空间,我就把自己放在这个空间里;如果我的前一个字符有指向我的字符的子节点时,我就放心地走到那个子节点就好了;最后记得更新x的值为当前处理的子节点的位置,并且s++,表示又多了一个单词进过了这个节点,以及完成val的修改之类的工作;
i++,进入下一重循环!
这样一棵完整的字典树就出来了!
模板&&模板题
【caioj 1463】统计前缀
题目描述
【题意】
给出很多个字符串(只有小写字母组成)和很多个提问串,统计出以某个提问串为前缀的字符串数量(单词本身也是自己的前缀).
【输入格式】
输入n,表示有n个字符串(n<=10000)
接下来n行,每行一个字符串,字符串度不超过10
输入m,表示有m个提问(m<=100)
第二部分是一连串的提问,每行一个提问,每个提问都是一个字符串.
【输出格式】
对于每个提问,给出以该提问为前缀的字符串的数量.
【样例输入】
5
banana
band
bee
absolute
acm
4
ba
b
band
abc
【样例输出】
2
3
1
0
就是一道裸题,查询时输出对应节点的s就好了;
附上代码:
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
struct node
{
int s,v[27];
node()
{
s=0;
memset(v,-1,sizeof(v));
}
}t[410000];
char a[410000];
int i,j,k,m,n,tot,js,jl;
int bt(int root)
{
int len=strlen(a+1);int x=root;
for(int i=1;i<=len;i++)
{
int y=a[i]-'a'+1;
if(t[x].v[y]==-1)t[x].v[y]=++tot;
x=t[x].v[y];t[x].s++;
}
}
int solve(int root)
{
int len=strlen(a+1);int x=root;
for(int i=1;i<=len;i++)
{
int y=a[i]-'a'+1;
if(t[x].v[y]==-1)return 0;
x=t[x].v[y];
}
return(t[x].s);
}
int main()
{
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
scanf("%s",a+1);
bt(0);
}
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%s",a+1);
printf("%d\n",solve(0));
}
}结语
通过这篇BLOG相信你已经掌握了Trie树,那就向着AC自动机前进吧!希望你喜欢这篇BLOG!
PS 字典树练习:
HDU1251(本题原版)
HDU1075
HDU1800
