感觉最近学的东西有点杂,最近复习了一下之前学习的匈牙利算法,突然发现,匈牙利算法解决的二分图问题竟然不只有二分图最大匹配问题!这篇Blog,我就来讲解一下匈牙利算法所解决的常见的四种模型吧!
什么是二分图
就是对于一个图中的所有点,都可以分类两个到集合X和Y,使得所有的边关联的两个顶点,恰好一个属于集合X,另一个属于集合Y。换句话说,就是集合X中任意两点间没有连边,集合Y中任意两点间也没有连边图。一般整理好之后如下:
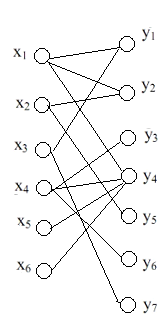
二分图最大匹配
我们先拿出一道经典的问题,来走进神奇的二分图吧!
【问题背景】
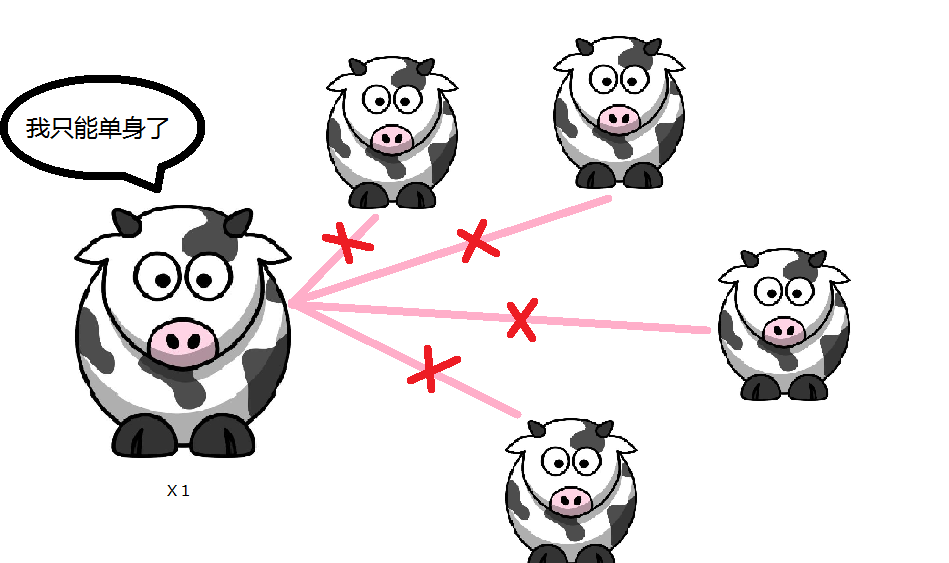
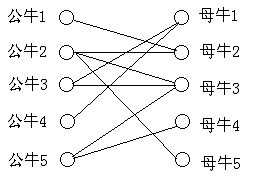
n只公牛和m只母牛,
某些公牛和某些母牛互相喜欢。
但最后一只公牛只能和一只母牛建立一对一匹配。
要使得最后牛群匹配对数最大。
【输入】
第一行三个整数n, m,k( 1<= n, m <= 10000,0< k < 100000)。
下来k行,每行两个整数 x,y,表示一条边,连接X集合中x点和Y集合的y点。
【输出】
只有一行。输出一个整数,表示牛群匹配对数最大值.
很明显,普通的DFS已经没办法解决这样规模的数据了;所以这是我们就要推出一个神奇的算法——匈牙利算法!!!那么这种神奇的算法要如何实现呢?下面我们就来一步一步讲解:
首先和暴力一样,我们对于每个公牛逐个找母牛匹配。如果公牛x1与母牛y1有匹配关系(map[x1,y1]==true),那么我们就来采访一下这只母牛y1:
如果母牛y1尚未匹配(match[y1]==0),则恭喜这对牛,他们匹配成功了,并且把母牛的丈夫设置为x1(match[y1]:=x1);


那么如果这只母牛已经有丈夫了呢?我们就去让母牛问一下他的丈夫x2(x2=match[y1]):如果x2能匹配到其他的母牛y2,那么x2就可以离开母牛y1了,与y2匹配了;这个时候y1就没有丈夫了,就可以嫁给公牛x1了。




那么如果y1的丈夫x2找不到其他能匹配的母牛呢?那没办法,这时候公牛x1不能再打y1的主意了;这时x1,只能再去寻找其他能和他匹配的母牛y2,y3.....




那么如果所有和他互相喜欢的母牛都无法和他完成匹配,那他就无法匹配,ans不变;其余情况能匹配,则ans++。
接下来让我们一步一步写完这个程序:
数据结构:
int match[501]; //标记母牛的数组,match[i]为第i只母牛的匹配对象是第几只公牛
int n,m,ans,i; //n公牛数目,m母牛数目,ans为匹配对数
bool map[401][501] ; //map[i][j]==true表示第i只公牛和第j只母牛有匹配关系
bool chw[501]; // 也是标记母牛可否被“询问”的数组(“询问”后面有解释)。
//如果第i只母牛chw[i]==false,表示母牛i不可被询问,否则表示母牛i可被“询问”。
//匈牙利算法的关键点:chw数组过程getmatch:从第1只到第n只公牛,逐个逐个寻找母牛匹配:
void getmatch()
{
ans=0;//匹配对数初始化为0
memset(match,0,sizeof(match));//每只母牛初始化为未匹配(match[i]=0)
for(int i=1;i<=n;i++) //公牛逐个逐个找母牛
{
memset(chw,true,sizeof(chw)); //所有母牛初始化为可“询问”
if(find_muniu(i)==true)ans++;//如果找到了,总体增加一对 find_muniu(i)表示公牛i去找母牛
}
}函数find(k):一个返回值函数判断第k只公牛能否匹配成功,若匹配成功返回True,若没有匹配成功返回false:
bool find_muniu(int k)
{
for(int i=1;i<=m;i++) //逐只母牛问
if (map[k][i]==true) //第k只公牛和第i只母牛有匹配关系
if (chw[i]==true)//问母牛i能否被“询问”
{
chw[i]=false; //标记母牛i已被询问,不管匹配成功与否,以后其他公牛都没必要再询问母牛i
if ( match[i]==0 || find_muniu(match[i])==true )
// match[i]=0 该母牛单身 或者 find(match[i])如果该母牛已匹配公牛x(x==match[i]),尝试让公牛x去找其他母牛匹配
{
match[i]=k;
return true; //这两句表示第i只母年匹配了第k只公牛}
}
}
return false;//执行到这一步表示匹配不成功。
}接下来我们来重点讲解一下“询问”:chw数组的意义。
意义一:如果第i只母牛 chw[i]==true ,表示第i只母牛有匹配成功的可能性。母牛i有未匹配和已匹配两种情况:
情况一:母牛i未匹配(match[i]==0),那么简单直接match[i]=k,匹配成功;
情况二:母牛i已匹配(X1==match[i]),那么让公牛X1尝试去寻找其他母牛匹配。公牛X1不能再找母牛i,否则成死循环。
意义二:如果第i只母牛 chw[i]==false,公牛X1也不能找已经被“询问”过的母牛j,为什么?母牛j被标记为“询问”过,分两种情况:
情况一:之前被询问的时候匹配成功了,或 match[j]=0或 find_muniu(match[j])=true。但情况一是不可能的。因为如果匹配成功,那么就不会有后来的公牛X1去找母牛j的需要。
情况二:之前被询问的时候匹配不成功。这种情况只能是母牛j已匹配,且匹配对象公牛X2(X2==match[j])找不到其他母牛匹配能成功(也就是find_muniu(X2)==false)。如果之前有其他公牛询问母牛j都不能成功,那么现在的公牛X1也一定不会成功,所以没有必要询问。chw数组的第二个意义剪支省时的作用。
主函数:
int main()
{
scanf("%d%d",&n,&m);//n只公牛,m只母年
memset(map,false,sizeof(map));//初始化匹配关系
for(int i=1;i<=n;i++)//读入边,构建图
{
int kk,y;scanf("%d",&kk); //混蛋,第i只公牛竟然能和kk只母牛匹配,她们是谁?
for(int j=1;j<=kk;j++)
{
scanf("%d",&y);
map[i][y]=true;
}
}
getmatch();
printf("%d\n",ans);//输出最大匹配对数
for(int i=1;i<=m;i++)//询问每只母牛有没有匹配到公牛
if(match[i]>0) //如果母牛i已经匹配,输出匹配了哪只公牛
printf("%d %d\n",match[i],i);
return 0;
}特别值得注意的是,当数据比较大时,二维数组map【n】【m】可能会超过空间限制,这时我们就要运用前向星进行存储。
二分图最小点覆盖
我们再来看一个例子:
【题目描述】
X集合有n个点(编号1,2,3,……n),
Y集合有m个点(编号1,2,3,……m),
有k条边(任意一条边的两个端点,一个来自X集合,一个来自Y集合)
如果选中一个点(可以来自X集合或Y集合)就燃烧掉所有与该点相连的边。
问:至少选中多少个点,可以摧毁所有边(也就是k条边)
【输入】
第一行三个整数n, m,k( 0< n, m < 100,0< k < 1000)。
下来k行,每行两个整数 x,y,表示一条边,连接X集合中x点和Y集合的y点。
【输出】一个整数,为最少选中的点数目。
什么你不会做?没事我先告诉你结论:按题意构图后,用匈牙利算法求最大二分图匹配数,就是答案!什么?你不会证明,没事接下来就让我慢慢证明给你看:
König定理证明:
虽然直接应用König定理可以解决许多最小覆盖的题目,但这类题难点往往在于构图,要做到灵活构图应用König定理,则对其证明需要有一定的了解。König定理的证明是建立在匈牙利算法操作细节上的,掌握匈牙利算法的全过程很重要。
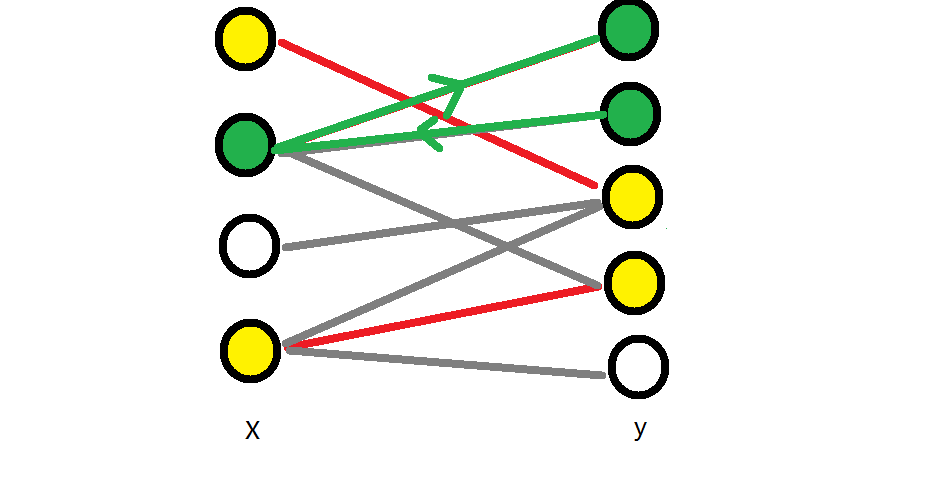
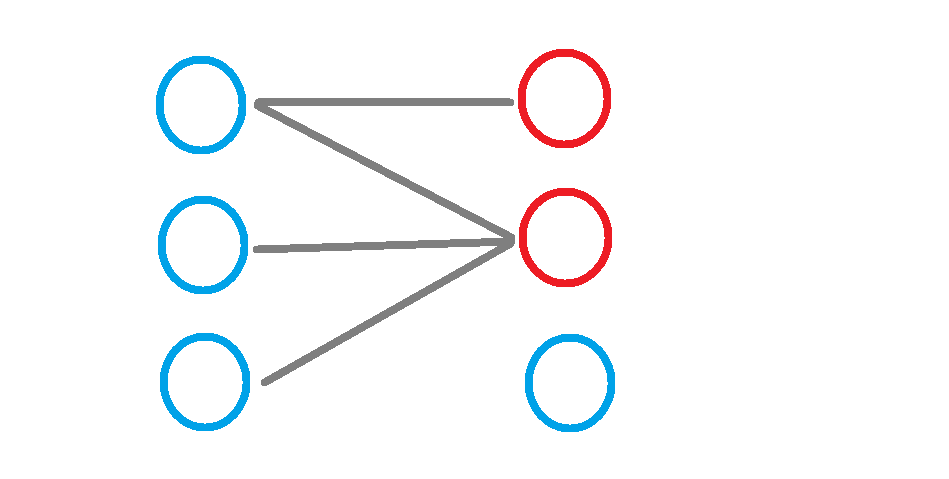
假设二分图G分为左边X和右边Y两个互不相交的点集。G经过匈牙利算法后找到一个最大匹配M=3,设红线为匹配边,黄色为匹配边两端的点如下图:

根据König定理,我们可以从最大匹配边中选M个点,使得这与这M个点相连的边刚好为总边数N。下来说明选点策略,再证明这个策略的正确性。
选点策略:
我们用绿色标记右边未匹配边的顶点,并从右边未匹配边的顶点出发,找到从该点出发所有满足边为未匹配→匹配→未匹配→……的原则的路径,并标记途中经过的顶点,值得注意的是任意一条路径最后一条经过的边必定为匹配边(否则为增广路经)。重复上述过程,直到右边不再含有未匹配边的点。
也就是所,我们每次都要先把右边的白色点标记成绿色,然后进行拓展;所以对于第一次拓展,我们首先标记右边的二号点,开始走边,得到绿色路径:
对于第二次拓展,我们首先标记右边的五号点,开始走边,得到绿色路径:
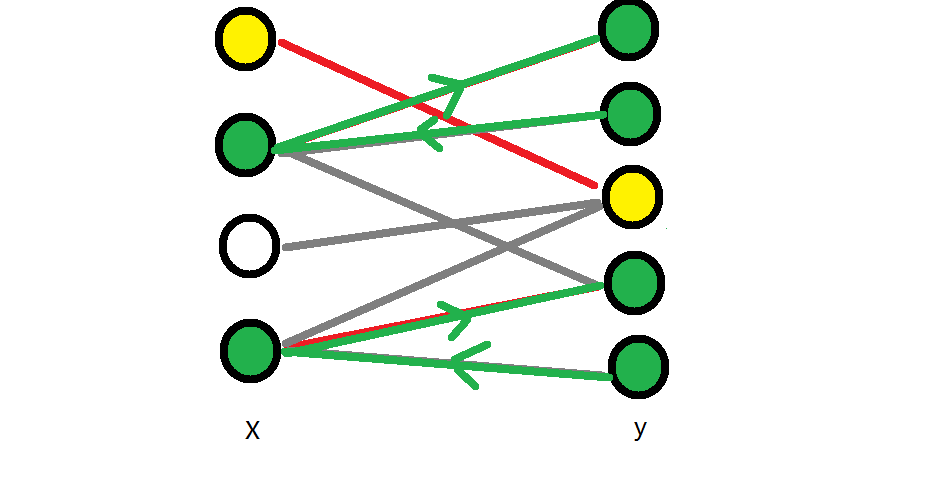
这时我们右边所有点都有了颜色,选点完成!这时我们记得到的左边已用绿色标记的点和右边未标记的点为S(用粉色标记),S即为所求的最小顶点集。
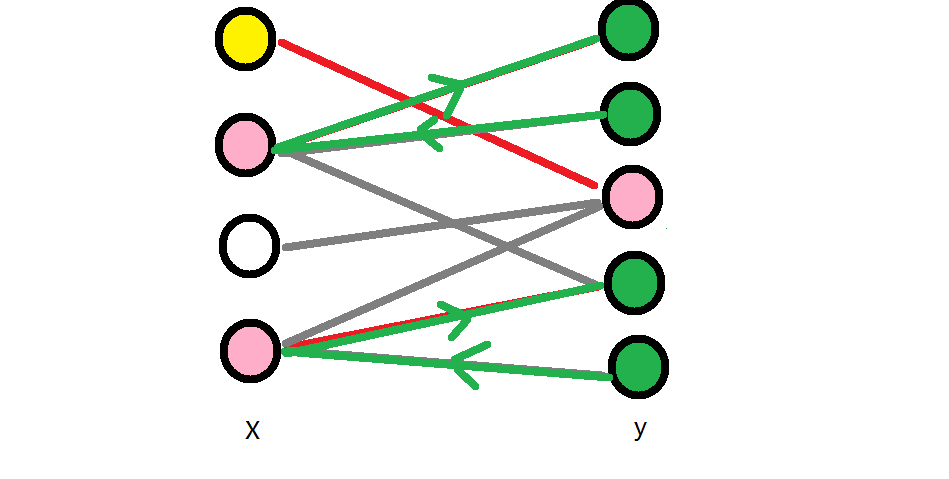
以下证明S即为所求的最小顶点集:
证明选点策略:
1、点集S的元素个数=二分图的最大匹配数M:
左边标记的点全都为匹配边的顶点,右边未标记的点也为匹配边的顶点。因此,我们得到的点与匹配边一一对应。
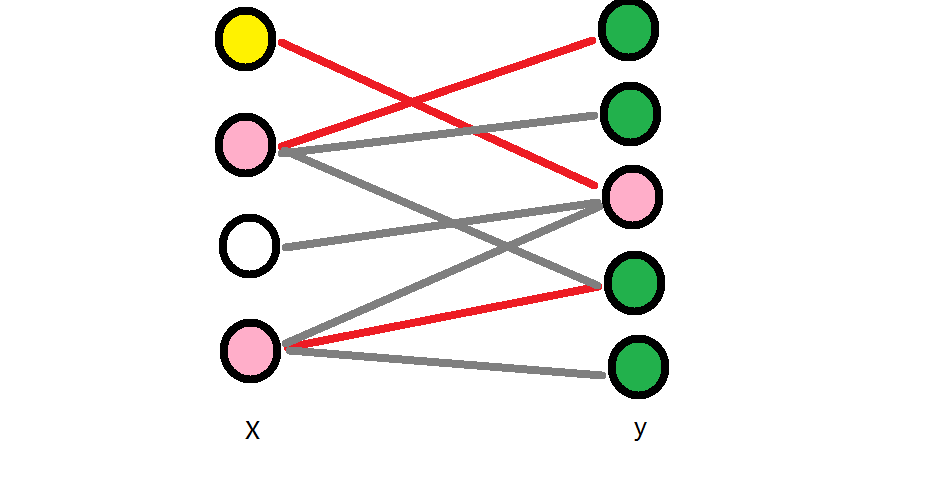
2、点集S中的点能覆盖二分图G中所有的边。
根据左右端点是否被标记,G中所有的边有以下四种情况:
① 左右均被绿色标记;
② 左右均无绿色标记;
③ 左边被绿色标记,右边未绿色标记;
④ 左边未绿色标记,右边被绿色标记;
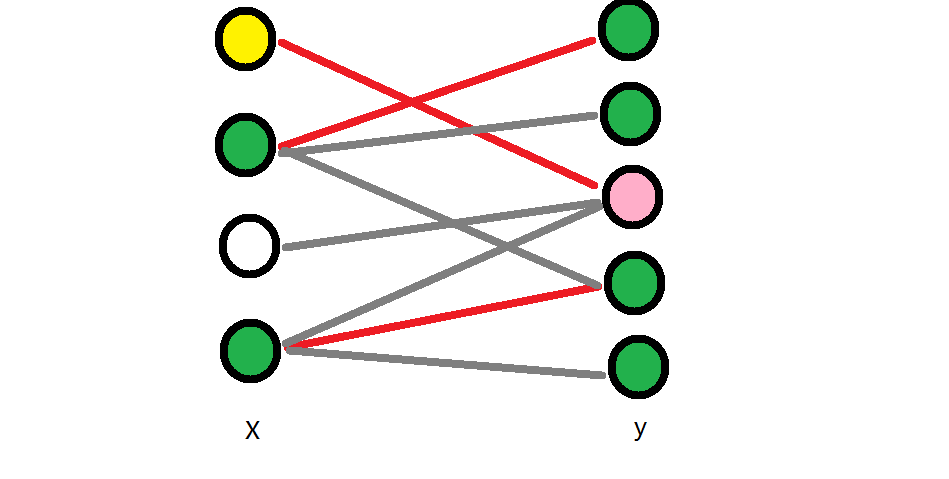
前三种,运用S中的点(包含:左边的点(标记)+右边的点(未标记))都能得到的,除了④。下面证明④不存在。
假如存在一条边e,使得e的两端都不在点集S当中,由于当时选点的时候选了二分图当中:左边为绿色的点和右边不为绿色的点;所以此时e的两个端点左边未绿色标记,右边被绿色标记;
如果e不属于被匹配的边(也就是之前过程中的绿色边),那么左端点就可以通过这条边右端点到达(从而得到标记);
如果e属于匹配边(也就是之前过程中的绿色边),那么右端点的标记从哪里来?它的标记只能是从这条匹配边的左端点过来,那么左端点就应该有标记。
3、S是最小的覆盖。
因为最大匹配M中,M条边两两之间没有共同交点,所以要覆盖这M条匹配边至少就需要M个点。
至此证明完成!
二分图最小边覆盖
我们再来看一个例子:
【题目描述】
X集合有n个点(编号1,2,3,……n),
Y集合有m个点(编号1,2,3,……m),
有k条边(任意一条边的两个端点,一个来自X集合,一个来自Y集合)
如果选中一条边就燃烧掉所有与该边相连的点。
问:至少选中多少个边,可以摧毁所有点
【输入】
第一行三个整数n, m,k( 0< n, m < 100,0< k < 1000)。
下来k行,每行两个整数 x,y,表示一条边,连接X集合中x点和Y集合的y点。
【输出】一个整数,为最少选中的边数目。
什么你又不会做,没关系,我们先把结论告诉你——我们先用匈牙利算法求最大二分图匹配数,再用总点数减去最大匹配数就是我们要求的的答案了。这是为什么呢?别急这就证明给你看:
我们首先设最大匹配数为m,总顶点数为n。为了使边数最少,又因为一条边最多能干掉两个点,所以尽量用边干掉两个点。也就是取有匹配的那些边,当然这些边是越多越好,那就是最大匹配了,所以先用最大匹配数目的边干掉大多数点。剩下的解决没有被匹配的点,就只能一条边干掉一个点了,设这些数目为a,显然,2m+a=n,而最小边覆盖=m+a,所以最小边覆盖=(2m+a)-m=n-m。
正如下图,我们先用最大匹配选出的三条边解决了黄色标记的六个点,剩下蓝色的三个点就没有办法了,没办法做到一条边覆盖两个蓝色点了,只好小亏一波,一条边去覆盖一个点。
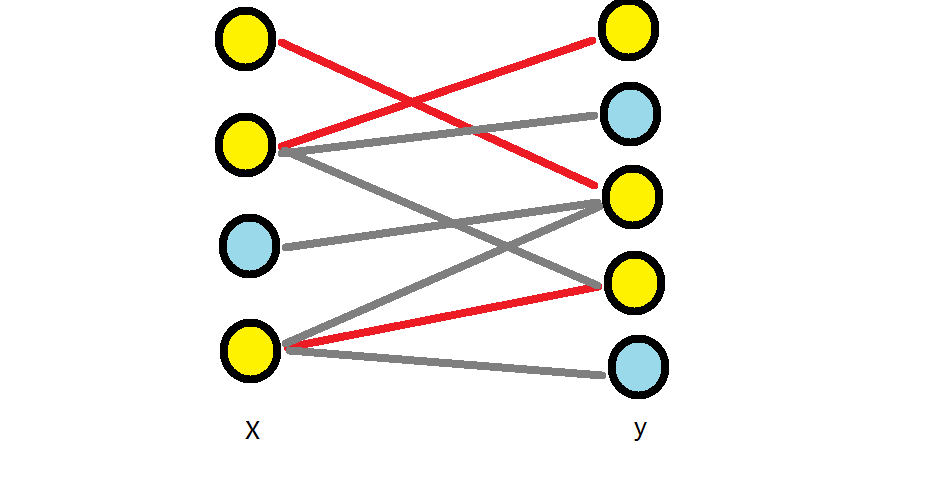
得证。
二分图最大独立集
我们同样的先引入一道例题:
题目描述
X集合有n个点,Y集合有m个点,同个集合内的任意两点没有边,
有k条边,每条边的两个端点一个来自X集合,另一个来自Y集合。
问题:选出某些点组成一个集合,使得集合中的任意两点之间没有边相连,问这个集合最多可以包含多少个点?
Input
数据第一行三个整数n, m (1 ≤ n, m ≤ 10000) and k (0 ≤ k ≤ n × m 且 k<= 10^6),
下来k行,每行两个整数 x and y (1 ≤ x ≤ n,1 ≤ y ≤ m), 表示一条边的两个端点。
Output
输出一行,一个整数,即集合最多可以包含点的个数。
还是先告诉你结论吧:
最大独立集=总点数 - 最小点覆盖=总点数 - 最大匹配数;
现在我们进入证明:
上图,我们用两个红色的点覆盖了所有边。我们证明的前提条件是已经达到最小覆盖(即满足:条件1.已经覆盖所有边;条件2.所用的点数最小)
首先我们来证明蓝色点组成的是一个独立集:
如果有两个蓝色点间有边相连,那么这条边则没有被覆盖,则与条件1矛盾。因此是独立集。
再来证明这个独立集最大:
如果我们要再增加这个独立集中的点,则需要把某个红点变成蓝点;那么此时我们就要把和这个红点相连的所用蓝点变为红点;
而由最小覆盖数=最大匹配数的证明我们知道,每一个红点是最大匹配中的一个匹配点;也就是说每个红点至少连接了一条边。因此当我们将某个红点变成蓝点时,我们需要牺牲的蓝点的个数是大于等于1的。也就是说,我们最多只能找到数量相等的其他独立集,而无法找到数量更大的。因此蓝色点集必定为最大独立集。
所以我们可以发现,蓝色点数 =总点数 - 红色点数,即最大独立集=总数-最小覆盖集。
至此证明完成!
结语
到这里,二分图的三种常见运用我们都已经讲完了,如果存在什么问题,请在下方留言中告诉我。希望你喜欢这篇BLOG!
guy