在之前的BLOG里，我们对几种主流的动态规划类型和常用的动态规划优化思路进行了讲解。而从这一篇开始，我们就要开始学习一些更加固定的技巧性的东西了。这篇BLOG就让我们从熟悉的单调队列出发，学习非常常用的斜率优化这一技巧吧！

单调队列

单调队列-滑动窗口

题目描述

给定一个长度为 $n$ 的数列，求长度为 $k$ 的定长连续子区间 $(a_1, a_2, \dots, a_k)$，$(a_2, a_3, \dots, a_{k + 1})$，……中每个区间的最大值和最小值。

解题思路

这是一道单调队列的模板题，单调队列有两个性质

1. 队列中的元素其对应在原来的列表中的顺序必须是单调递增的。
2. 队列中元素的大小必须是单调递*(增/减/甚至是自定义也可以)

单调队列与普通队列不一样的地方就在于单调队列既可以从队首出队，也可以从队尾出队。那么我们应该怎样实现单调队列呢?

就拿样例来谈谈，设以最小的为标准。

8 3
1 3 -1 -3 5 3 6 7

下文中我们用q来表示单调队列，p来表示其所对应的在原列表里的序号。

1. 由于此时队中没有一个元素，我们直接令1进队。此时，q={1},p={1}。
2. 现在3面临着抉择。下面基于这样一个思想:假如把3放进去，如果后面2个数都比它大，那么3在其有生之年就有可能成为最小的。此时，q={1,3},p={1,2}
3. 下面出现了-1。队尾元素3比-1大，那么意味着只要-1进队，那么3在其有生之年必定成为不了最小值，原因很明显:因为当下面3被框起来，那么-1也一定被框起来，所以3永远不能当最小值。所以，3从队尾出队。同理，1从队尾出队。最后-1进队，此时q={-1},p={3}
4. 出现-3，同上面分析，-1>-3，-1从队尾出队,-3从队尾进队。q={-3}，p={4}。
5. 出现5，因为5>-3，同第二条分析，5在有生之年还是有希望的，所以5进队。此时，q={-3,5},p={4,5}
6. 出现3。3先与队尾的5比较，3<5，按照第3条的分析，5从队尾出队。3再与-3比较，同第二条分析，3进队。此时，q={-3,3},p={4,6}
7. 出现6。6与3比较，因为3<6，所以3不必出队。由于3以前元素都＜3，所以不必再比较，6进队。因为-3此时已经在滑动窗口之外，所以-3从队首出队。此时，q={3,6},p={6,7}
8. 出现7。队尾元素6小于7，7进队。此时，q={3,6,7},p={6,7,8}。

那么，我们对单调队列的基本操作已经分析完毕。因为单调队列中元素大小单调递*(增/减/自定义比较)，因此，队首元素必定是最值。按题意输出即可。

简单来说，单调队列的核心思想就是如果一个选手比你小还比你强，那你就永远都打不过他了。

了解了单调队列的原理之后，下面就让我们来看看单调队列如何优化我们的动态规划问题吧。

最长上升子序列

题目描述

给定N个数，求这N个数的最长上升子序列的长度。

解题思路

我们设 $f[i]$ 表示第 $i$ 个数必选的最长上升子序列。$f[i] = max(f[j] + 1)$ $j < i$ 且 $a[j] < a[i]$。在 $1 \space 9 \space 7 \space 8 \space 4 \space 3 \space 5 \space 8$ 当中，当求解了 $f[3]$ 之后，就没必要考虑某个数接在 $9$ 后面了。因为 $7$ 的存在使得 $9$ 没有机会了。保留 $1 \space 7$ 即可。

到 $4$ 的时候， $4$ 和 $7$ 往前的最长上升子序列长度是一样的，而且 $4 < 7$，所以 $7$ 也没机会了，让 $4$ 替换掉 $7$ 的位置，保留 $1 \space 4 \space 8$（分别对应 $f$ 值为 $1 \space 2 \space 3$）。

所以我们每次可以用一个队列维护留下了还有机会往后面加数的数字，显然是单调递增的。每次我们就在这个队列中二分出第一个大于等于 $a[i]$ 的位置，并将这个位置的值更新为 $a[i]$。

[CF940E]Cashback

题目描述

给你一个长度为 $n$ 的数列 $a$ 和一个整数 $c$，你可以把他们分成任意长度的若干段，每一段可以去掉前 $\lfloor \frac{k}{c} \rfloor$ 小的数字（$k$ 是这一段的长度），求最后剩下的数的和最小是多少。$1 \le n,c \le 10^5$。

解题思路

很容易想到设 $f[i][j]$ 表示前 $i$ 个数分为 $j$ 段所删去的数的最大和。那么我们很容易会有 $f[i][j] = f[l][j - 1] + val[l + 1, i]$，其中 $val[l + 1, i]$ 表示从 $(l + 1, i)$ 中 $\lfloor \frac{i - l}{c} \rfloor$ 的数的累加和。

接着我们就会发现其实这个 $j$ 这一维是没有任何用处的，所以我们可以设 $f[i]$ 为前 $i$ 个数删去的数的最大和，这样就优化方程为 $f[i] = f[l] + val[l + 1, i]$。

我们继续发现，假如我们取了一个长度为 $x$ 且 $x < c$ 的区间，那在这个区间中不会删去任何的数，所以不会优于取若干个长度为 $1$ 的区间。 我们继续考虑，假如我们取一个长度为 $x = 2c$ 的区间，这样取的最小和次小值的和一定小于等于分为两个长度为 $c$ 的区间分别的最小值的和。所以对于一个更普遍的区间长度 $x \% c \neq 0$，不会优于取若干个长度为 $c$ 的区间和长度为 $1$ 的区间。所以我们的方程可以变成 $f[i] = max(f[i - 1], f[i - c] + val[i - c + 1, i])$。而这个 $val[i - c + 1, i]$ 其实就是区间 $(i - c + 1, i)$ 的最小值，定长区间维护最小值很容易想到滑动窗口，用单调队列即可轻松解决。

[POJ2373]DIVIDING THE PATH

题目描述

在一片草场上：有一条长度为 $L(1 \le L \le 10^6, L \text{为偶数})$ 的线段。 $John$ 的 $N(1 \le N \le 10^3)$ 头奶牛都沿着草场上这条线段吃草，每头牛的活动范围都是一个开区间 $(S, E)$，$S, E$ 都是整数。不同奶牛的活动范围可以有重叠。 $John$ 要在这条线段上安装喷水头灌溉草场。每个喷水头的喷洒半径可以随意调节，调节范围是 $[A, B](1 \le A \le B \le 10^3)$，喷洒半径可以不是整数。要求线段上的每个整点都恰好位于一个喷水头的喷洒范围内，每头奶牛的活动范围要位于同一个喷水头的喷洒范围内，任何我喷水头的喷洒范围不可越过线段的两端（左端是 $0$，右端是 $L$）。请问 $John$ 最要要安装多少个喷水头。

解题思路

我们设 $f[i]$ 表示覆盖完全 $[0, i]$ 区间的草时用到的最少的喷水头的数量。也就是说对于 $i$ 作为右边界，我们要枚举一个左边界进行专一，我们有如下转移方程：$f[i] = min(f[j] + 1)$ 其中 $(2A \le i - j \le 2B)$。特别地如果 $i$ 在一个奶牛的活动范围当中则直接设 $f[i]$ 为 $+\infty$。

所以我们又变成了定长区间取最小值，又转换成了滑动窗口问题，所以我们使用单调队列进行维护。

[POJ3017]Cut the Sequence

题目描述

给定一个长为 $n(1 \le n \le 10^5)$ 的序列，求一种分割方式使得每部分都满足和不超过 $M$ 的情况下每部分的最大值和最小，求出这个最小值。保证 $A[i] \ge 0$。

解题思路

设 $f[i]$ 为前 $i$ 个数取到的最小值，那么我们很显然就可以有 $f[i] = min(f[i], f[j] + max(a[j + 1], a[j + 2], \dots, a[i]]))$，其中 $j \le i$ 且 $sum[i] - sum[j - 1] \le M$。

设 $a[j + 1], a[j + 2], \dots, a[i]$ 中的最大值为 $a[k]$，而在这题中 $f$ 数组显然是不减的，所以我们有 $f[j + 1] + a[k] \le f[j + 1] + a[k] \le \dots \le f[k - 1] + a[k]$，所以这一段显然只有 $dp[j + 1] + a[k]$ 可能贡献到答案。也就是说如果某一段到当前位置 $i$ 的最大值都一样，那就只取靠前的就可以了。

由这个性质，我们很容易可以联想到单调队列来维护一个递减的队列，存的是符合要求的某一段的最大值。但是需要注意的是，队首元素不一定是最优的，由于队列元素递减但是 $f$ 递增，所以队列当中的所有元素都有可能组成最优解。

[NOI2005]瑰丽华尔兹

题目描述

不妨认为舞厅是一个 $N$ 行 $M$ 列 $(1 \le N, M \le 200)$ 的矩阵，矩阵中的某些放个上堆放了一些家具，其他的则是空地。钢琴可以在空地上滑动，但是不能撞上家具或滑出舞厅，否则会顺坏钢琴和家具。引来难缠的船长。

每个时刻，钢琴都会随着船体倾斜的反向相邻的方格滑动一格，其中相邻的方格可以是向东、向西、向南或向北的。而艾米丽可以选择施展魔法或不施展魔法。如果不施展魔法，则钢琴会滑动，而如果施展魔法，则钢琴会原地不动。艾米丽是个天使，她知道每段时间的船体的倾斜情况。她想使钢琴尽量长的时间在舞厅里滑行，但她还太小不会计算，所以希望你帮助她。保证时间段 $K \le 200$，总时间 $T \le 40000$。

解题思路

最基本的我们可以设 $f[i][j][k]$ 表示在第 $k$ 个单位时间到达 $(i, j)$ 处的最长滑行距离，那就会有 $f[i][j][k] = max(f[i][j][k - 1], f[i'][j'][k - 1] + 1)$，其中 $(i', j')$ 为相邻的按这一时刻滑行方向划过来的格子。但这样就是 $O(NMT)$ 的显然会超时。

我们考虑如何进行优化，我们可以吧同方向滑动的时间划分成同一段来处理，我们设 $f[i][j][k]$ 表示在第 $k$ 段时间末尾到达 $(i, j)$ 处的最长滑行距离。考虑从上一时间段转移过来，如果不撞上障碍物，以向下滑动为例转移方程就应该为 $f[i][j][k] = max(f[i'][j][k - 1] + i - i')$，其中 $i - i' \le t$ 即不大于这一段的最大滑动时间。这样做的话我们的时间复杂度就是 $O(max(N,M)NMK)$ 的。

我们继续发现，我们的式子可以变成 $f[i][j][k] = max(f[i'][j][k - 1] - i') + i$，也就是说其实我们的决策其实和 $i$ 是多少没什么关系，而只和 $f[i'][j][k - 1] - i'$ 有关。所以对于这一轮决策，对于某一列的值更新其实就是长度为 $t$ 的定长区间的最大值，那就是每一列跑一个滑动窗口。那由障碍怎么办？其实也很好处理，出现障碍也就是之前的点都没法更新后面的点了，所以我们直接清空我们的单调队列就可以了。向左滑动向右滑动向上滑动和我们上面这个向下滑动其实是一样的就不再赘述了。

然后 $K$ 这一维可以压缩掉，可以压缩成 $01$ 或者算出一列的更新量在计算完整一列后才进行更新也可。

多重背包问题

题目描述

有N种物品和一个容量为V的背包。第i种物品最多有n[i]件可用，每件费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

解题思路

之前使用二进制拆分，比如 $11 = 1 + 2 + 4 + 4$，通过这 $4$ 件物品可以将 $0 \sim 11$ 都表示出来，这样就从 $O(nv \sum c[i])$ 变成了 $O(nv \sum log(c[i]))$，其中 $c[i]$ 表示第 $i$ 件物品的件数。我们接下来考虑怎么继续优化。

我们设 $f[i][j]$ 表示前 $i$ 件物品体积为 $j$ 的最大价值，那么我们显然有 $f[i][j] = max(f[i - 1][j - k * v[i]] + k * w[i])$，其中 $k$ 表示取了第 $i$ 件物品 $k$ 件，那么显然要满足 $0 \le k \le c[i]$。我们发现决策和 $j$ 和 $k$ 都有关不好优化，所以我们第一时间的想法就是 $j$ 和 $k$ 中选择一个干掉，通过人类经验积累我们觉得 $j$ 比较好干掉。

我们令 $a = j / v[i]$，$b = j \% v[i]$，那么就有 $j = a * v[i] + b$。所以我们代换 $j$ 改写方程为 $f[i][j] = max(f[i - 1][a * v[i] + b - k * v[i]] + k * w[i])$，我们设 $k' = a - k$，那么我们有 $f[i][j] = max(f[i - 1][b + k' * v[i]] + (a - k') * w[i])$，我们将 $a$ 提到外面就有 $f[i][j] = max(f[i - 1][b + k' * v[i]] - k' * w[i]) + a * w[i]$，那么在这里我们范围就是 $a - c[i] \le k' \le a$。可以发现在 $j$ 的情况下最多塞入 $a$ 个，所以这里的 $k'$ 表示的就是第 $i$ 种物品有多少个能塞但不塞进去。

我们观察式子 $f[i - 1][b + k' * v[i]] - k' * w[i]$ 只与 $k’$ 有关，而这个 $k'$ 是从 $0$ 开始连续到 $a$ 的。所以我们要做的就是求出 $f[i - 1][b + k' * v[i]] - k' * w[i]$ 在 $k$ 取可行区间内的最大值就可以了，这个可以用单调队列来维护。

斜率优化

[HNOI2008]玩具装箱

题目描述

教授要去看奥运，但是他舍不下他的玩具，于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩，其可以将任意物品变成一堆，再放到一种特殊的一维容器中。

$P$ 教授有编号为 $1...N$ 的 $N(1 \le N \le 5 * 10^4)$ 件玩具，第 $i$ 件玩具经过压缩后变成一维长度为 $C_i(1 \le C_i \le 10^7)$.为了方便整理， $P$ 教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物，形式地说如果将第i件玩具到第j个玩具放到一个容器中，那么容器的长度将为 $x=j-i+\sum(C_k)$，其中 $i ≤ k ≤ j$。

制作容器的费用与容器的长度有关，根据教授研究， 如果容器长度为 $x$, 其制作费用为 $(X-L)^2$。其中 $L(1 \le L \le 10^7)$ 是一个常量。$P$ 教授不关心容器的数目，他可以制作出任意长度的容器，甚至超过 $L$。但他希望费用最小。

解题思路

既然我们的题目中有 $\sum(C_k)$，很自然地想到先用 $sum[i]$ 维护 $C[i]$ 的前缀和。那么假设 $f[i]$ 表示前 $i$ 个玩具装好的最小花费，那我们很自然就有 $f[i] = min(f[j] + cost(j + 1, i))$。

我们展开 $cost(j + 1, i)$ 得到 $f[i] = min(f[j] + (sum[i] - sum[j] + i - (j + 1) - L)^2)$，化简得到 $f[i] = min(f[j] + (sum[i] +i - sum[j] - j - 1 - L)^2)$。那我们发现，我们的转移的代价既和我们当前点 $i$ 的一个式子有关，又和我们转移点 $j$ 的一个式子有关，很自然地想到把和 $i$ 相关的放在一起，把和 $j$ 相关的放在一起。

所以我们设 $a[i] = sum[i] + i$，$b[i] = sum[i] + i + L + 1$，可以看出 $a[i]$ 和 $b[i]$ 都是单调递增的。假设我们的最优转移点就是 $j$ ，我们的式子就变成了 $f[i] = f[j] + (a[i] - b[j])^2$，拆开就是 $f[i] = f[j] + a[i]^2 + b[j]^2 - 2a[i]b[j]$，我们将只含有 $j$ 的放在左边，移向就是 $f[j] + b[j]^2 = 2a[i]b[j] + f[i] - a[i]^2$。由于我们考量的是选择哪个 $j$ 进行转移，所以我们的 $j$ 是主角，只和 $i$ 相关的都可以看作是常数。

我们将式子改写成 $Y = KX + B$ 的形式，$X$ 和 $Y$ 都是和决策有关也就是和 $j$ 有关的，而 $K$ 和 $B$ 都是常数也就是最多只与 $i$ 有关的。那么有 $Y = f[j] + b[j]^2$，$K = 2a[i]$，$X = b[j]$，$B = f[i] - a[i]^2$。

这样做有什么作用呢？我们的目标是让 $f[i]$ 尽量小，而 $a[i]^2$ 是一个定值，所以我们的目标可以转化成让 $B$ 尽量小。所以我们的问题就变成了找一个直线，它过 $(X, Y)$ 即 $(b[j], f[j] + b[j]^2)$，斜率为 $2a[i]$，让它的截距最小。对于一点 $i$ 此时斜率是定值了，所以对于所有小于 $i$ 的 $j$ 我们都画出它的 $(X, Y)$ ，并画出对应的直线：

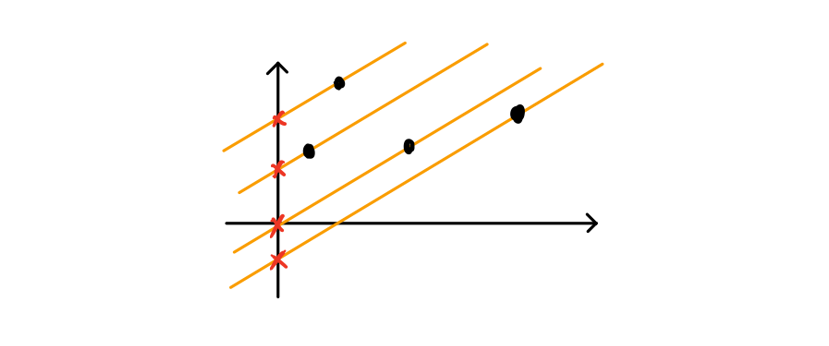
然后我们考虑动态的过程，随着我们 $i$ 的增大，我们直线斜率 $K = 2a[i] = 2(sum[i] + i)$ 也是单调递增的。我们考虑下图这样一个过程，我们开始时 $i$ 对应的斜率为紫色直线，后面随着 $i$ 的增大，斜率变大变成了蓝色直线。

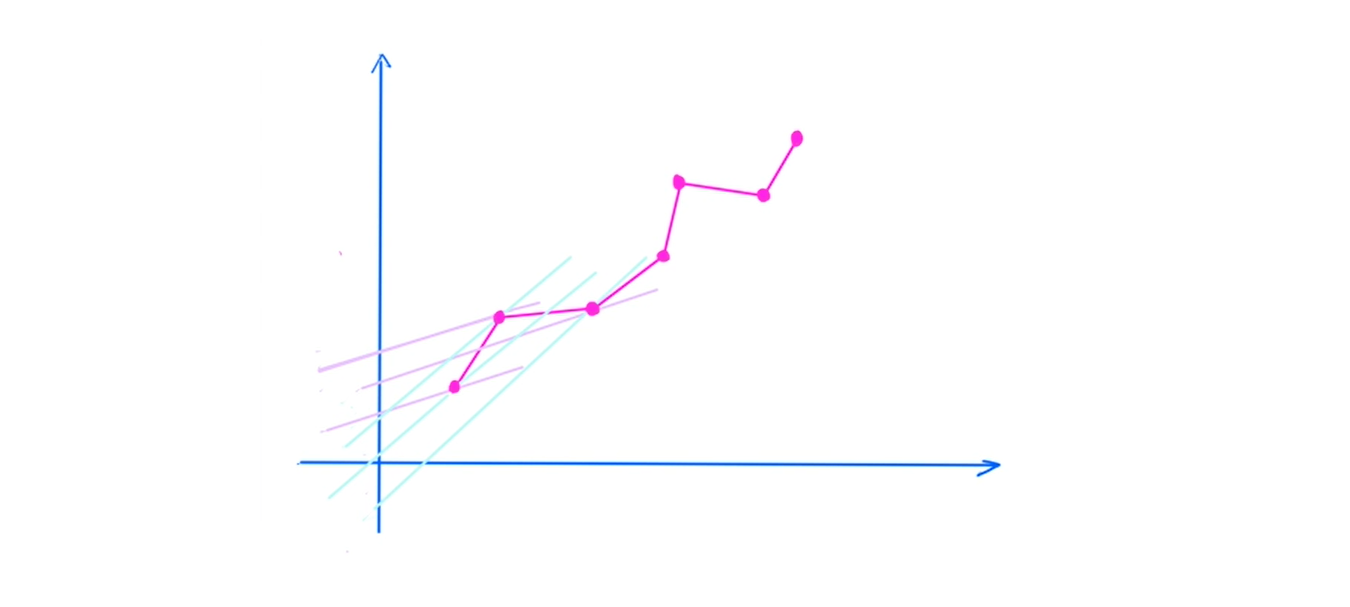
我们的答案在 $i$ 比较小的紫色直线时，过第一个点的直线的截距最小，贡献答案；而在 $i$ 比较大的蓝色直线时，过第三个点的直线截距最小，贡献答案。不妨你也手玩一下，你发现不管斜率怎么增大，我们的第二个点一直不可能成为答案，所以我们可以把第二个点删掉。

所以我们就要维护一个类似于下凸壳的东西，下凸壳上的点才有可能作为答案。我们发现在这个下凸壳我们每条边的斜率是递增的，对于一条给定斜率的直线截距则是先减后增的，所以很容易想到可以三分。

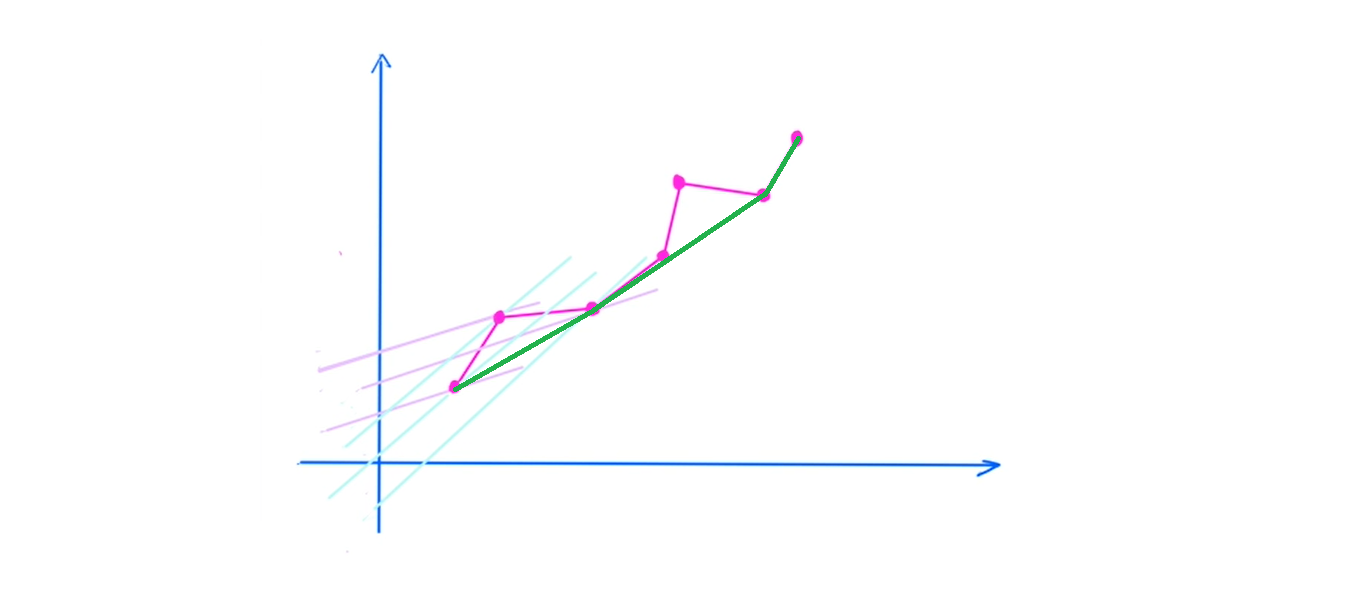
但仔细想想，其实是可以不用三分的。随着我们斜率的增加，越在我们下凸壳后面的点越有可能能成为我们的答案。换言之我们维持这个下凸壳就是为了斜率增加后找到下凸壳后面的点来达到真正的答案。所以每次操作我们就比较下凸壳的前两个点对应直线的截距，如果第一个点对应直线的截距大于第二个点对应直线的截距，那之后再随着我们斜率的继续增大，我们第一个点只会越来越劣，是永远不可能成为答案的，这时我们直接将队首退队就可以了。如此重复多次直到队首最优或者只剩下队首这一个元素。所以每次我们的队首就是答案。

总的来说我们就是搞一个单调递增的单调队列也就是平时用来维护最小值的单调队列来维护我们的下凸壳，对于每一个 $i$，我们先将 $i-1$ 的相关值从队尾插入，按照单调队列的方法将不太优的队尾弹出。然后不停考察队首两个元素直到队首元素优于第二个元素。最后输出答案就是队首元素对应直线的截距。

代码实现

按照上面的思路，我们可以写出代码如下。

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
struct node {
    long long x, y;
    int site;
}q[550000];
int st, ed; 
int n;
long long c[550000], s[550000];
long long a[550000], b[550000];
long long f[550000];
long long L;

double calc(node A, node B) {
    double y = A.y - B.y;
    double x = A.x - B.x;
    return(y / x);
}
int main() {
    scanf("%d%lld", &n, &L);
    for(int i = 1; i <= n; i++) {
        scanf("%lld", &c[i]);
        s[i] = s[i - 1] + c[i];
        a[i] = s[i] + i;
        b[i] = s[i] + i + L + 1;
    }

    a[0] = 0; b[0] = L + 1;
    st = 1; ed = 2;
    q[1].x = q[1].y = 0; q[1].site = 0;
    for(int i = 1; i <= n; i++) {
        while(st < ed - 1) {
            long long A = f[q[st].site] + (a[i] - b[q[st].site]) * (a[i] - b[q[st].site]);
            long long B = f[q[st + 1].site] + (a[i] - b[q[st + 1].site]) * (a[i] - b[q[st + 1].site]);
            if(A > B) st++;
            else break;
        }
        f[i] = f[q[st].site] + (a[i] - b[q[st].site]) * (a[i] - b[q[st].site]);

        node temp;
        temp.x = b[i];
        temp.y = f[i] + b[i] * b[i];
        temp.site = i;
        while(ed - st >= 2) {
            if(calc(temp, q[ed - 1]) < calc(q[ed - 1], q[ed - 2])) ed--;
            else break;
        }
        q[ed++] = temp;
    }

    printf("%lld", f[n]);
    return 0;
} 

之前题目的斜率优化

最长上升子序列

$f[i] = max(f[j] + 1)$，那考虑转移点为 $j$ 就有 $1 = -f[j] + f[i]$，在这里写成 $y = kx + b$ 的话就是$x = f[j]$， $y = 1$ ，$k = -1$，$b = f[i]$。就是过 $(1, f[j])$，目标让截距 $b = f[i]$ 尽量大。由于斜率小于 $0$，点又都是 $(1, f[j])$ 的形式。我们看下图就发现要让截距尽量大，那每次肯定都是选取能选的最右的点。但由于要单调上升，所以并不是每个点都能选取，我们就要用我们上面的单调队列维护能选取的点，然后二分找到最右的点。

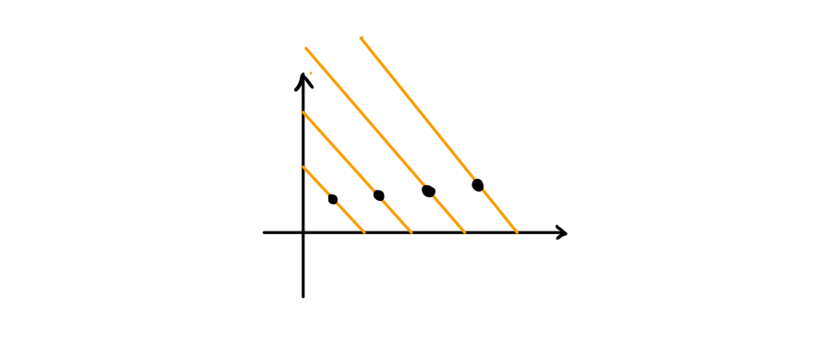
Cashback

$f[i] = min(f[i - 1] + a[i], f[i - c + 1] + sum[i] - sum[i - c] - Min[i])$,那考虑转移点为 $i - c + 1$ 就有 $f[i] = f[i - 1] + a[i], f[i - c + 1] + sum[i] - sum[i - c] - Min[i]$，我们移向得到 $sum[i] - sum[i - c] - Min[i] = -f[i - c + 1] + f[i]$。在这里写成 $y = kx + b$ 的话就是$x = f[i-c+1]$， $y = sum[i] - sum[i - c] - Min[i]$ ，$k = -1$，$b = f[i]$。所以我们就是对于斜率为 $k = -1$，过定点 $(f[i-c+1], sum[i] - sum[i - c] - Min[i])$，让截距 $b = f[i]$ 尽量大。而当 $c$ 增大时，我们的 $x$ 是单调递减而 $y$ 是单调递增的。

所以在下图中你发现，当 $3$ 号点出现的时候，我们的 $2$ 号点就没有存在的必要了，这就是我们单调队列的过程。

Cut the Sequence

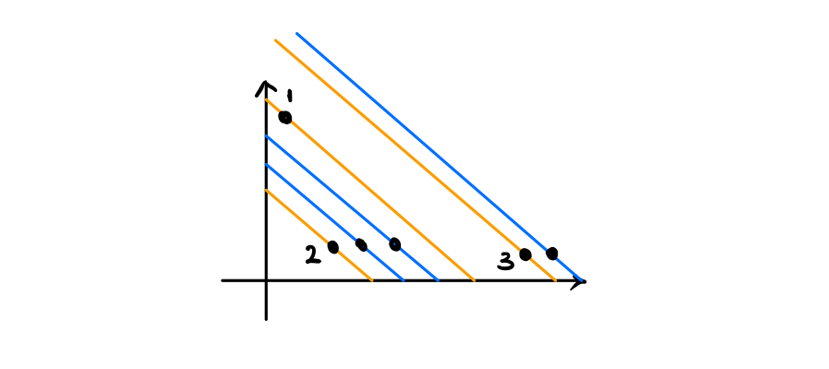
$f[i] = min(f[i], f[j] + max(a[j + 1], a[j + 2], \dots, a[i]))$，那考虑转移点是 $j$ 就有 $f[i] = f[j] + max(a[j + 1], a[j + 2], \dots, a[i])$，我们移向就有 $max(a[j + 1], a[j + 2], \dots, a[i]) = -f[j] + f[i]$。我们将其写成 $y = kx + b$ 的形式的话就是 $x = f[j]$，$y = max(a[j + 1], a[j + 2], \dots, a[i])$，$k = -1$，$b = f[i]$。就是过 $(f[j], max(a[j + 1], a[j + 2], \dots, a[i]))$，目标让截距 $b = f[i]$ 尽量小。当 $j$ 递增的时候我们的 $f[j]$ 单调递增，$max(a[j + 1], a[j + 2], \dots, a[i])$ 单调递减，我们画出图就可以发现，当最大值一样我们就选取最前面也就是 $j$ 最小的就可以。但对于不同的最大值并不是 $j$ 越小截距越大，所以对于每个不同最大值对应的点都要进行考量。

结语

通过这篇BLOG，我们发现单调队列一般是处理斜率优化当中，斜率 $k$ 恒定的情况。而一般的斜率优化是在决策点单调，即 $(x, y)$ 中的 $\frac{x}{y}$ 单调。斜率单调的时候用单调队列维护斜率，每次决策点就在队首；斜率不单调的时候就用二分在单调队列上面找。

决策点不单调怎么办？就算决策点再不单调，我们还是只有一个下凸壳是有用的，所以我们就需要维护一个动态凸包，这就要用到平衡树或者 $CDQ$ 分治了。

最后希望你喜欢这篇BLOG！