最近准备总结一下常用的字符串算法，今天就让我们从最经典的回文串算法——Manacher开始吧！

什么是回文串

“回文串”，就字面而言，就是是一个正读和反读都一样的字符串。比如“level”就是一个回文串，但是“love”就不是一个回文串。

那么如何求解回文串呢？朴素的来想，我们只需要枚举原序列中的点k，接着从k点向左右拓展直到拓展到的左端和右端字符不一样；这样操作就可以得到一个O(n^2)的算法。

但是1975年，一个叫Manacher的十分聪明的人发明了一个算法，并命名为Manacher算法（中文名：马拉车算法），运用该算法可以把时间复杂度提升到O(n)。

下面就让我们一起走进神奇的Manacher算法。

Manacher过程详解

首先，由于回文串分为奇数长度的回文串和偶数长度的回文串，为了方便处理，我们在开头结尾以及任意两个字符之间都插入一个“%”，这样我们就只用考虑长度为奇数的回文串就可以了。

接下来就是Manacher的精髓了。我们对于任意一个点i，都定义一个值 p【i】 表示 以 i 为中心的最长回文的半径。

例如对于一个字符串 a b b a h o p h p ；第一次操作后得到序列 % a % b % b % a % h % o % p % h % p % ；接下来我们手算一下p数组——

可以看出，p[i] - 1正好是原字符串中最长回文串的长度。

关键就在于如何快速求解p数组，如果利用暴力求解，不就和暴力一样了吗？

首先，我们需要定义两个全局变量:

pos：表示当前求解到的所有回文串中，右端点最右的回文串的中心在哪里;
r:表示pos所在中心的字符串的右端点究竟在哪里。

如下图，我们把方框当成回文串，则我们很明显的看到，浅黄色的回文串的右端点在最右边，所以以它的中点为pos，右端点为r：

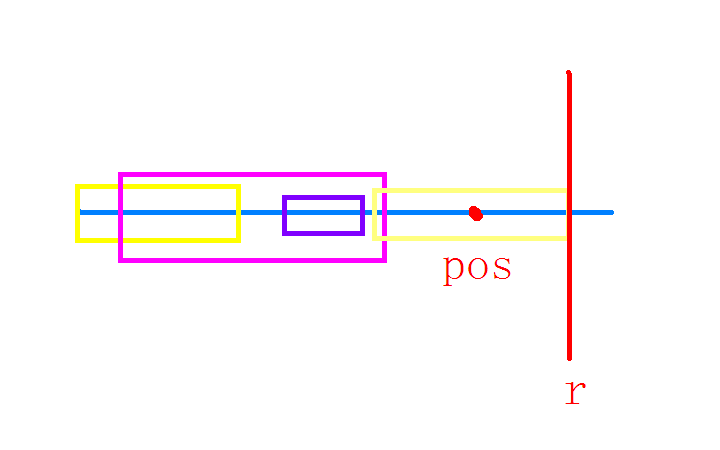
也就是说，我们每求得一个新的回文串，就要尽可能的更新一次pos和r。

接下来让我们回到求p【i】的问题上来，假设我们现在求p[i]，也就是以 i 为中心的最长回文半径，那么我们只要对i分成两种情况：

1.i＜＝r 也就是说，i在 以 pos 为中心的回文串内；

这样的话有什么好处吗？我们观察一下下面这幅图：

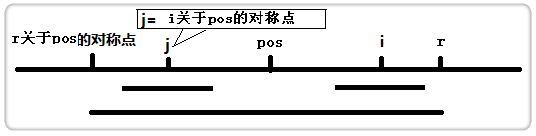
我们用黄色方框以j为中心的回文串，此时又分为两种情况：

1.当j的回文串比较短，在以pos为中心的回文串之内：

由于i，j同在一个回文串内，且关于pos对称，所以以i为中心的红色回文串一定有一个和黄色回文串相同；即此时p【i】=p【j】；

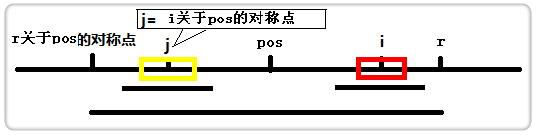
2.当j的回文串比较长，超出了以pos为中心的回文串：

此时，以i为中心的回文串的最右只能到r；

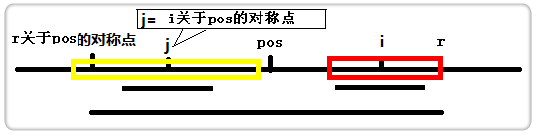
为什么不能和以j为中心的回文串等长呢？我们看下图，若此时，以i为中心的回文串（记为紫色）和以j为中心的回文串（记为红色）等长，那么两段绿色的字符也肯定相同，那么以pos为中心的回文串最右就不是到r了呀！

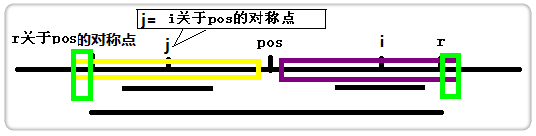
所以此时两段绿色内的字符一定不同，固以i为中心的回文串的最右只能到r。

2.i＞r 也就是说，i在 以 pos 为中心的回文串外；

那么此时，我们就已经没有参照的j之类了，这时只要老老实实的向左右两边拓展就好了。

总的复杂度为O（n）。

代码实现

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
char s[12000000],now[24000000];
int i,j,k,m,n,len,pos,r,ma;
int p[24000000];
int my_min(int x,int y)
{
    return x<y?x:y;
}

int my_max(int x,int y)
{
    return x>y?x:y;
}

int manacher(char *s)
{
    for(int i=1;i<=len;i++)
    {
        now[i*2-1]='%';
        now[i*2]=s[i];
    }//进行操作一，插入%

    len=len*2+1;now[len]='%';
    pos=0;r=0;//初始化pos，r

    for(int i=1;i<=len;i++)
    {
        if(r>=i)p[i]=my_min(p[2*pos-i],r-i);//情况1；
        else p[i]=1;
        while(1<=i-p[i] && i+p[i]<=len && now[i-p[i]]==now[i+p[i]])p[i]++;//应对情况2，向两边拓展
        if(i+p[i]>r)
        {
            r=i+p[i];
            pos=i;
        }
        ma=my_max(ma,p[i]-1);
        //更新r，pos，最长回文串长度ma
    }
}
int main()
{
    scanf("%s",s+1);
    len=strlen(s+1);ma=0;
    manacher(s);
    printf("%d",ma);
    return 0;
}

结语

通过这篇博客，相信你已经学会了Manacher，感兴趣的同学可以去Luogu p3805完成这道模板题，运用Manacher，速度也相当可观。

希望你喜欢这篇Blog！