GDOI Cu滚出了好难受啊QwQ。今天早上目送完参加Day3的大佬后，就去听了中大严紫熙的《网络流的沧海一粟》，收获良多。现在我们就来简单介绍一下简单的网络流算法和一些推论和经典技巧吧！

什么是网络流问题

我们最常见的问题是最大流问题：

问题表述：给定一幅图（n个结点，m条边），每一条边有一个容量，现在需要将一些物品从结点s（称为源点）运送到结点t（称为汇点），可以从其他结点中转，求最大的运送量。

在介绍最大流问题的解决方法之前，先介绍几个概念：反向弧，残余网络，增广路径，最大流定理。

反向弧：

若从 u 到 v 的边的容量为 c ，这条边上有流量 f 流过（称为正向弧），则相当于从 v 到 u 有一条容量为 0 的边，其流量为 - f ，这条边就是反向弧 。

反向弧的意义：反向弧的作用是起到有更优决策的时候会使当前选择的弧会自动放弃。反向弧有流量的原因是因为如果刚刚选择了正向弧，下一次如果存在更优策略使这 f 的流量流入汇点，就可以选择反向弧，将流量 f 撤销。

残余网络：

计算出图中的每条边上容量与流量之差（称为残余容量），即可得到残余网络。注意由于反向边的存在，残余网络中的边数可能到达原图中边数的两倍。

举例如下：观察上图的网络，这种状态下它的残余网络如下图所示：

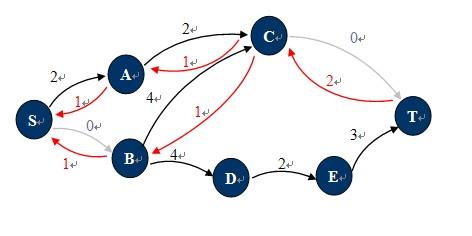
增广路径：

残余网络中任何一条从 s 到 t 的有向道路都对应一条原图中的增广路径 —— 只要求出该道路中所有残量的最小值 d ，把对应的所有边上的流量增加 d 即可，这个过程称为增广。

最大流定理：

如果残留网络上找不到增广路径，则当前流为最大流；反之，如果当前流不为最大流，则一定有增广路径。

这样的话，求解最大流就只需要在残余网络中寻找增广路，直到不存在可以从 s 流向 t 的增广路，此时即为最大流。

网络流算法鼻祖

现在主要的网络流算法有dicnic，sap，isap和像非递归sap+dicnic的一些奇奇怪怪优化的网络流算法。但是要追其鼻祖，还是要谈起FF（Ford-Folkerson)算法，那么这种算法究竟是如何实现的呢？

其实啊,网络流的精髓就是寻找增广路,FF也不例外。利用增广路，找到一条从源点到汇点的任意路径，所有边上的最小值delta如果不是0，那么总流量就可以增加delta，在将路径上的边的容量减去delta，这就是一条增广路。

易知，如果找不出增广路了，那么此时的流量就是最大了。

但是，就这样还不行，如果走的不够优“走错了”怎么办？

所以现在我们引进“反向弧”，反向弧可以解决这个问题。其他的博客上很多说反向弧可以让流量后悔，这个比喻很生动，但用我自己的话来说，反向弧因为是同原边反向的，两者中一者减去delta时，将另一者加上delta，那么之后找增广路时，走反向弧相当于原边少走，非常巧妙。

代码如下：

#include<cmath>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#define INF 2147483647
using namespace std;
int read(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
struct edge{
    int next,to,head,b;
}f[440000];
long long ans;
int tot=0,n,m,s,t;
bool mark[400000]={0},flag;
void add(int u,int v,int w){
    f[tot].next=f[u].head;f[u].head=tot;f[tot].to=v;f[tot].b=w;tot++;
}
int dfs(int x,int flow){//dfs求任意路径
    if(x==t){
        ans+=flow;
        flag=1;
        return flow;
    }
    mark[x]=1;
    for(int i=f[x].head;i!=-1;i=f[i].next){
        int x1=f[i].to;
        if(mark[x1]||f[i].b==0) continue;
        int delta=dfs(x1,min(flow,f[i].b));
        if(flag){
            f[i].b-=delta;
            f[i^1].b+=delta;
            return delta;
        }
    }
    return 0;
}
void FF(){//有增广路就增广
    memset(mark,0,sizeof(mark));
    flag=0;
    dfs(s,INF);
    while(flag){
        memset(mark,0,sizeof(mark));
        flag=0; 
        dfs(s,INF);
    }
}
int main(){
    n=read();m=read();s=read();t=read();
    for(int i=1;i<=n;++i) f[i].head=-1;
    while(m--){
        int x,y,w;x=read();y=read();w=read();
        add(x,y,w);add(y,x,0);
    }
    FF();
    printf("%lld",ans);
    return 0;
}

可以说是非常暴力了。

对FF算法的一些理解

现在我们在了解了FF算法后，可以从中推到出一些东西。

1.FF算法执行完后，图必定有割

什么叫割呢？我们知道，每个网络流的图都有一个源点和一个汇点，如果我们把可流量为0的点删去，源点和汇点无法相连，那么就说这个图出现割了！

简单来说，就说这幅图断成了两部分，源点连接一部分，汇点连接另一部分，如下图：

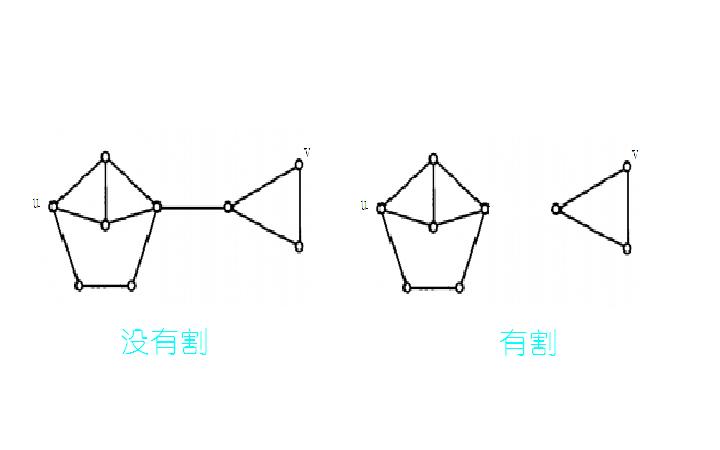
那么显然，在FF算法执行完后，图必定有割！否则就还存在从源点到汇点的流，FF算法就必然可以继续执行下去。

2.入边具有等效性

我们考虑如果每条边都有两条入边，无论流那条边的流量，其实对于总流量的贡献都是一样的。由于这个等效性，所以对于任意可行流，FF算法得出来的流都会大于等于该流。

由上述我们认知：

1.FF的流量一定小于等于任意割的容量；
2.FF穷尽所有的流，所以任意的流都不能大于FF的流。

又当FF流尽时造成了割，且FF的流量等于他造成的那种割的容量。所以最大流等于最小割！

理解流和割

1.可以认为流是可以流转各个节点的东西，比如资源和物品的移动；
2.可以认为割真的割断某个图的割；
3.可以认为是割的决策，不做多余决策由最小割的性质保证。

一些建模技巧

1.流的中转如果变成了不同种类的流，可以通过把一个点裂成两个点来解决；
2.如果流的代价运算是乘法，由于网络流算法是加法运算，所以可以取对数变为加法；
3.不等式方程可以通过增加冗余变量变为等式；
4.其中某些决策限制可以通过割的性质使其满足；
5.在某些情况可以补取来转变流和割。

结语

我们这次简单地介绍了一下网络流的基本性质和一些推论技巧！在下一篇BLOG里，我们会着重

介绍一些常见的模型。希望你喜欢这篇BLOG！！！