相信树形动态规划大家都已经很熟悉了，不熟悉的同学可以点击链接进行巩固复习。而在树形动态规划之上，还有一种 “PLUS树形” 动态规划，也就是我们接下来要提到的基环树动态规划，这种动态规划一经出现就席卷了各大平台。下面就让我们一同看看吧。

基环树

在图论中，树被视作为一种特殊的图 $G=(V, E)$，其中$|V| = |E|+1$。其存在如下特性：

• 树 $G$ 上任意两点必定能够通过途经若干边后到达；
• 任意两点间的路径必然唯一，即不存在环；
• 将树 $G$ 上任意一条边删去，该图即成为非连通图；
• 在 $G$ 中任意不相连两点间插入一条边，该新图 $G’ =(V, E’)$ 正好含有一个环。

基环树，也称为基环外向树、环套树，其概念即是从上述特性 $4$ 所引申出的特殊的树，即是从树 $G$ 上两个不相连的点中插入一条边所得到的特殊的图，就是有一个环然后环上的每个节点都是一棵树，大概如下所示。

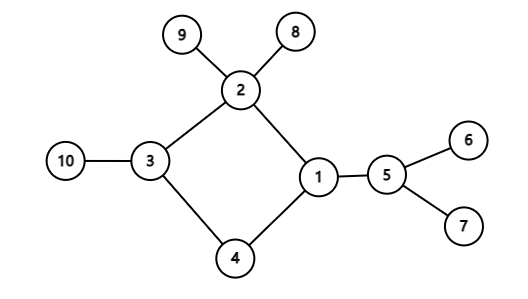
虽然其不符合树 $|V| = |E| + 1$ 的特征，但由于其特殊性——删除环上任意一条边即可成为树，故在许多基环树动态规划上，仍将其视作”树”来解决问题。

经典例题

[$ZJOI2008$]骑士

问题描述：有 $n$ 个骑士，每个骑士有个战斗力 $val_i$ 以及一个最厌恶的人（保证不会厌恶自己），现在我们要从所有的骑士中选出一个骑士军团，使得军团不存在一个骑士与他最痛恨的人一同被选入骑士军团的情况，并且使得这支骑士军团最具有战斗力，一个军团的战斗力为所有骑士的战斗力总和。（$n ≤ 10^6$）

这个题面一看就有一种熟悉感，没错如果是一棵树的话就是一个简单的树形$DP$——没有上司的舞会。这道题由于每个人都有一个厌恶的人，所以就算有 $n$ 个点 $n$ 条边，也就是比树多一条边。现在实际上就是一个环，环上的每个点向外都是一个树的结构，我们一般叫它基环外向树简称基环树又叫环套树。像基环树或者仙人掌这些都是特殊的图，有着比图更好的性质，一般都能帮助我们找到更好的方法去解题。

那我们这道题怎么做呢？我们先写个搜索/拓扑排序/并查集之类的先找到这个环上的一条边，然后我们如果把环上断掉一条边，那我们的题目就变成了树上的也就是没有上司的舞会。

但是我们做树上的$DP$保证不了我们断掉的这条边连接的两个点不同时选。处理方法也非常简单，我们设断掉这条边链接的两个点为 $u$ 和 $v$，我们先从 $u$ 出发以 $u$ 为根，做一遍树上的 $DP$，做过没有上司的舞会这道理的同学都知道，我们的状态是 $f[i][0/1]$ 分别代表第 $i$ 个点选或者不选的情况下以 $i$ 为根的子树的最大价值，所以最后我们只要取 $f_1[u][0]$ 就能保证 $u$ 不选进而就能保证 $u,v$ 不同时选；同样地我们在从 $v$ 出发以 $v$ 为根，再做一遍树上的 $DP$，最后取 $f_2[v][0]$ 就能保证 $v$ 不选进而也就能保证 $u,v$ 不同时选。然后我们取这两次树形 $DP$ 的最大值也就是 $f_1[u][0], f_2[v][0]$ 就是答案。当然最后还有一点必须要注意，这个图可能不连通，所以就有多个基环外向树，那也一样对每个基环外向树都做一下就好了。

[$NOI2013$] 快餐店

问题描述：就是给你一个有 $n$ 个点 $n$ 条边的联通无向图，然后要你找出一个点（可以在边上），使得这个点到所有图上的点距离最大值最小。（$n \le 10^5$）

我们看到 $n$ 个点 $n$ 条边又是联通简单的，就是一个基环外向树了。解决基环树的题目，我们首先还是考虑先在树上怎么做。在树上的情况，显然就是找到树的直径，然后答案就是直径的长度除以二。这是因为，首先我们到树的直径上两个点的最短距离的最大值至少已经是树的直径的一半也就是 $\frac{len}{2}$，下面我们证明不会有点距离直径的中点超过 $\frac{len}{2}$，这是因为若存在一个点距离这个中点超过了 $len / 2$，那么我们就找到新的直径了！也就是之前的直径就不是最远的两点了，这当然产生了矛盾。

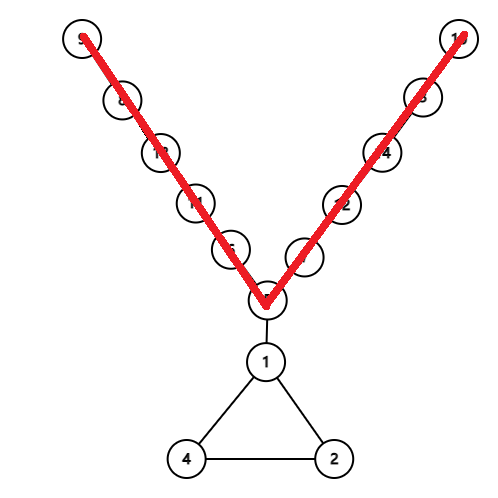
接下来我们考虑有环的情况，最简单的一种方法就算取考虑环上总有一条边不会走到，对于两点之间的最短路径我们不可能在环上走一圈，所以我们可以枚举环上的边，删掉它，然后求直径。时间复杂度$O(n^2)$，这样的复杂度显然是不能通过的。我们考虑能不能不要每次都求直径？ 然后我们看我们的直径有哪些情况，一是在外向树的内部和我们的基环一点关系没有：

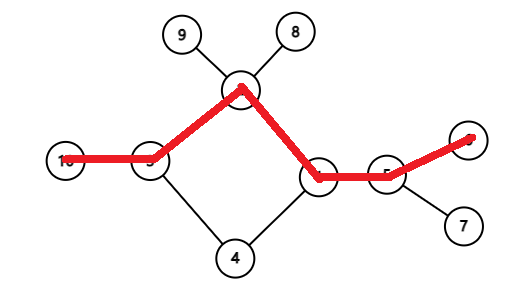
二是经过了环上的边，这时我们就要枚举基环，看看从哪个点把基环断开：

我们着重考虑第二种情况，我们先预处理出环上所有点所在子树的最大深度为 $d[i]$。我们先把环从 $first$ 到 $last$ 展开（没删边，可以用虚线）。

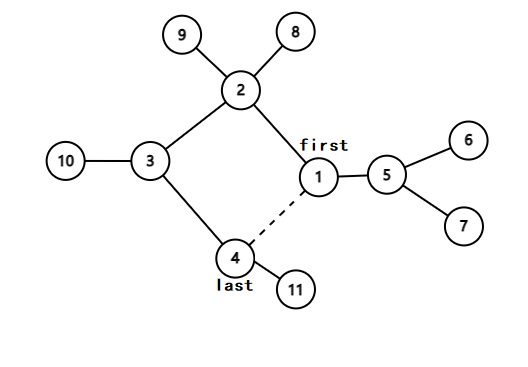
然后设环上第 $i$ 个点离环的第一个点的距离为 $pre[i]$，离环上最后一个点的距离为 $sub[i]$。然后我们再维护四个数组：环上第一个点出发到 $i$ 点的子树或者他左边的子树的最大距离 —— $d[i] + pre[i]$ 的前缀最大值；环上最后一个点出发到 $i$ 点的子树或者他右边的子树的最大距离 —— $d[i] + sub[i]$ 的后缀最大值； $i$ 点之前的最大直径——$d[x] + d[y] - pre[x] + pre[y]$；$i$ 点之后的最大直径——$d[x] + d[y] + pre[x] - pre[y]$。后两个如何维护？类似于序列最大子串。对于 $i$ 这个位置，相当于从 $i$ 断开，对上面三种$A[i],B[i],C[i]+D[i+1]+dis(first, last)$求 $max$，但是这个并不是我们真正的直径，比如例子中的红线不如橙线，我们走的不是最短路径。这样走会导致我们在环上本应该走短边的走了长边。

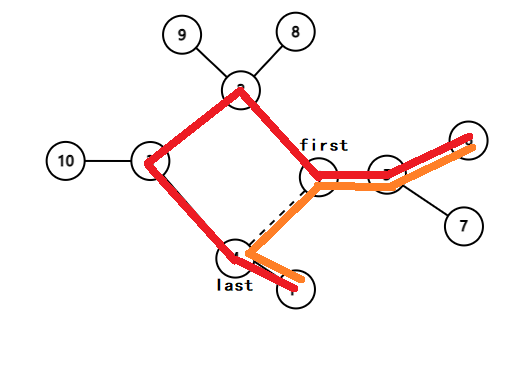
那我们怎么处理呢？其实在另一处 $j$ 会把我们的短边留下来作为 $j$ 的答案，所以我们对所有 $i$ 求 $min$ 就是我们的答案。这是因为我们总有一条边不会走走到，其实我们删掉一条边然后跑直径的 $O(n^2)$ 做法，也是有可能绕环上长边的，我们就是枚举断环上的边求直径然后取 $min$ 就是我们的答案。我们断开了真正直径在环上的边时，我们就要去绕环的长边，我们最后的答案是会变大的！而我们的直径不可能全部边都在同一条直径上，所以我们是枚举断环上的边求直径然后取 $min$。回到我们正解求的就是 $i$ 和 $i+1$ 断开的直径，只是我们现在可以快速维护了。

[$NOI2012$]遗失游乐园

问题描述：有一个 $n$ 个点 $m$ 条边的无向联通图($m = n - 1$ 或 $m = n$ )，先从 $n$ 个点当中等概率地选择一个点作为起始点，接着每一步都会随机去一个和当前点有道路相连的点，并且同一个点不去两次（包括起始点），直到当前点的所有相邻点都已经访问过为止。问期望路径长度。

首先我们观察题目，$m=n/n-1$ 也就是可能是树也可能是基环外向树。我们还是照例先考虑树上的情况。

首先是个树的就比较简单，就是简单的换根 $DP$ 就可以解决。我们线任选一个根，$f[i]$ 表示从 $i$ 节点出发走到其子树路径的期望长度。那么 $f[x] = \frac{sum(f[son]+a[i])}{numson[i]}$，其中 $a[i]$ 为 $son$ 到 $x$ 的边长，$sumson[i]$ 为 $i$ 的儿子个数，这个我可以用度数表示——根节点的 $numson$ 就是他的度数 $du[i]$，其他点是度数减一。然后我们考虑用换根的方法维护出每个点为根（起点）时期望路径长度。然后我们考虑从 $x$ 是根变成其儿子 $y$ 是根，那么 $f'[x] = \frac{f[x] * du[x] - a[x][y]-f[y]}{du[x] - 1}$ 并且 $f'[y] = \frac{f[y] * (du[y] - 1) + a[x][y] + f'[x]}{du[y]}$。

接下来我们考虑是基环外向树的情况，我们先用树形$DP$对环上的每个外向树进行求解，求出环上的每个点向下走的录井长度的期望。对于环上的每个点，除了往下走还可以往左往右走，所以枚举它的左右两边断掉，拆成链。在链上推一遍就可以得到这个点王座或往右走的路径期望长度。用这两种期望长度再去更新这个点，然后在这个点对应的子树再跑换根就可以了。这道题保证环中节点个数$\le 20$，复杂度大概是 $O(2n + k^2)$，所以是不会 $TLE$ 的。

其实还有另外一种解法，可以不需要换根。我们刚刚提到每个点有两类走法，一是往子树跑二是往上报。所以我们把 $i$ 点第一步往儿子走的期望路径长度记作 $f[i]$，儿子个数记作 $son[i]$。在把第一步往父亲/环上相邻点走的期望路径长度记作 $g[i]$，父亲/环上相邻点个数记作 $fa[x]=1/2$。那么从 $i$ 出发的期望路径长度 $= \frac{f[i] * son[i] + g[i]*fa[i]}{son[i] + fa[i]}$。接下来我们分情况讨论，如果 $i$ 不在环上，$x$ 是 $i$ 的父亲，那么 $g[i] = a[x][i] + \frac{g[x] * fa[x] + f[x] * son[x] - f[i] - a[x][i]}{fa[x] + son[x] - 1}$，即先走到 $x$，然后从 $x$ 出发任意走但不能走回 $i$；如果 $i$ 在环上，那我们就枚举环上的点，先计算它顺时针走到环上另外每个点 $x$ 的概率 $p[x]$，其实我们规定顺时针就相当于断了边。在这一个点它可以继续顺时针走或者钻到子树里面去，由于一头扎进去的概率是 $\frac{son[x]}{son[x] + 1}$，所以 $g[i] += (\frac{down[x] * son[x]}{son[x] + 1} + dis[i][x]) * p[x]$，顺时针的最后一个点只能钻到子树里面，所以 $g[i] += (down[x] + dis[i][x]) * px$。然后同理计算逆时针的就可以了。我们把环上的 $g[i]$ 求完了再去子树里面的 $up$ 即可。

结语

通过这篇 $BLOG$，相信你已经对基环树以及其对应的动态规划问题有了一定的了解。其实在大多数情况下，基环树问题都可以先放在树上的情况先行进行讨论，然后再考虑加上一条边后的变化。具体来说一般是处理环上的和外向树上的关系。最后希望你喜欢这篇 $BLOG$！