概率是我们日常生活中随处可见的东西，但就是这么一个平常看起来平易近人的东西在遇上动态规划组合成概率$DP$的时候，就往往会让人血压升高抓耳挠腮。这篇$BLOG$，我将和你一起窥探概率$DP$的冰山一角，大致了解其解题思路和应对方法。

概率动态规划

要了解概率动态规划也就是概率$DP$，我们要先了解一下什么是概率。所谓概率就是反映随机事件出现的可能性大小的量度比如掷骰子出 $6$ 点的概率。而与概率相关的一个概念就是数学期望，数学期望（$mean$）或均值亦简称期望是实验中每次可能结果的概率乘以其结果的总和，是最基本的数学基本特征之一，它反映随机变量平均取值的大小，有点类似于我们的加权平均。举个例子，我们掷均匀的骰子掷出点数的期望就是 $ \frac{1}{6}*1+\frac{1}{6}*2+\frac{1}{6}*3+\frac{1}{6}*4+\frac{1}{6}*5+\frac{1}{6}*6 = 3.5$。

那我们为什么要研究期望呢？下面呢我们来看一下一个现实的问题。

问题描述：甲乙两个人赌博，他们两人获胜的几率相等，比赛的规则是先胜三局者为赢家，赢家可以获得 $100$ 法郎作为奖励。当比赛进行到第四局的时候，甲赢了两局，乙赢了一局。这时由于某些原因中止了比赛，那么如何分配这 $100$ 法郎比较公平？

首先我们知道最后的比赛结果要不是甲赢，要不是乙赢，所以分给甲的钱应该是 $100 * P_{甲赢}$，分给乙的钱应该是 $100 * P_{乙赢}$。我们先算乙获胜的概率，乙要赢比赛后面两局都必须拿下所以概率是 $\frac{1}{2} * \frac{1}{2} = \frac{1}{4}$，那甲获胜的概率就是 $1 - \frac{1}{4} = \frac{3}{4}$。所以分给甲的钱应该是 $100 * \frac{3}{4} = 75$，分给乙的钱应该是 $100 * \frac{1}{4} = 25$。这个值未必是最后游戏玩完后的结果，但这就是当前局面获得钱的期望，也是比较公平的分配方法。

而概率$DP$就是用于解决概率问题与期望问题，一般情况下，解决概率问题需要顺序循环，而解决期望问题使用逆序循环，如果定义的状态转移方程存在后效性问题，还需要用到高斯消元来优化。概率$DP$也会结合我们之前学习的其他知识动态规划知识进行考察，例如状压$DP$和树形$DP$等。下面就让我们通过例题来体会一下吧。

经典例题

Happy Running

问题描述：小明需要在操场顺时针跑圈打卡，操场上有两个打卡点 $A,B$，他需要现在 $A$ 点打卡，然后在 $B$ 点打卡（哪怕B在A前面）,打完卡就可以结束跑步了，他的起点以及 $A,B$ 的位置是随机的，告诉你操场的长度是 $X$ 米，求他跑超过 $K$ 米的概率。

概率的题目能算对样例就成功一半了，这里给的样例输入是先给出 $K$ 再给出 $X$。样例有 Input:2 2 Output:0.50，Input:4 3 Output:0.22，Input:2 1 Output:0.00。第一次见到这种题目难免会束手无策，没事我们慢慢来。

由于起点以及 $A,B$ 的位置是随机的，但其实我们可以等价于起点固定 $A,B$ 的位置是随机的。这时我们分类讨论：

• 如果 $A$ 在 $B$ 的前面，这时小明跑的距离是小于一圈了，实则就是跑了 $B$ 的距离，这适用于 $K < X$ 的情况。所以这个时候我们的约束就是：$\begin{cases}
  K < X, \ A < B, \ B > K, \ A、B \le X
  \end{cases}$，由于都是连续的点所以取不取等号其实完全不影响答案。那我们画出图出图，发现可行的其实就是阴影部分：
  

  所以我们的概率就是阴影部分面积除以总的面积就是 $\frac{\frac{1}{2}X^2-\frac{1}{2}K^2}{X^2}$。

• 如果 $A$ 在 $B$ 后面，那小明就要先跑一圈再跑到 $B$，实则就跑了 $X+B$ 的距离，这适用于 $K > X$ 的情况。所以这个时候的约束就是：$\begin{cases}
  K > X, \ A > B, \ B + X > K, \ A、B \le X
  \end{cases}$，转换一下变成$\begin{cases}
  K > X, \ A > B, \ B > K - X,\ A、B \le X
  \end{cases}$。我们画出图，可行区域还是阴影部分：
  

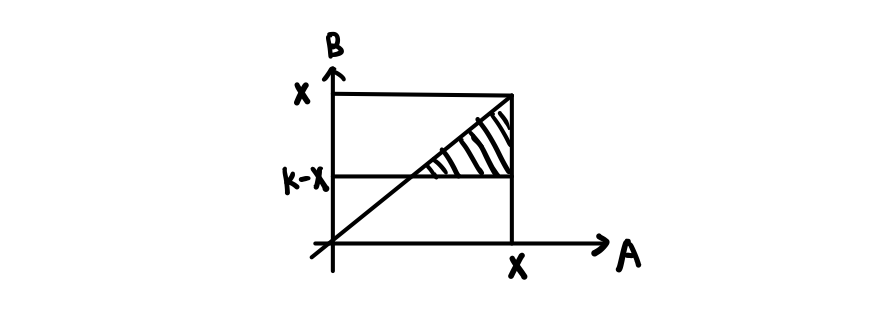
  所以我们的概率就是阴影部分面积除以总的面积就是 $\frac{\frac{1}{2}K^2}{X^2}$。

• 最难的情况还是 $K=X$ 的情况。真正去算可能要用极限之类的知识，实在不会算的话可以观察样例输出 $0.50$。这样我介绍一种较为简单的感性方法。其实要让我们跑的距离超过 $K$ 而 $K = X$ 也就是要超过一圈就两种情况：一是我们的 $A$ 在 $B$ 的前面，且 $B$ 无限接近于起点，这样就刚好跑一圈；二是 $B$ 在 $A$ 的前面，这样就一定要跑 $X+B > X \ge K$ 的距离。然后我们发现第一种情况， 且 $B$ 无限接近于起点的概率其实是趋向于 $0$ 的，第二种情况的约束就是 $\begin{cases}
  B > A,\ A、B \le X
  \end{cases}$，可行区域还是阴影部分：
  

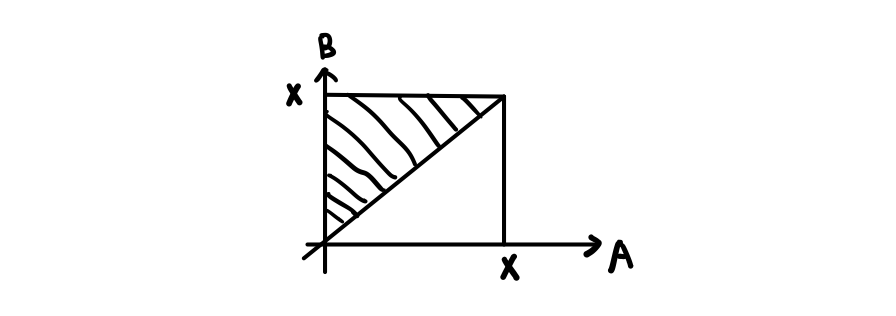
  所以我们的概率就是阴影部分面积除以总的面积就是 $\frac{\frac{1}{2}X^2}{X^2}=\frac{1}{2}$。

到这里这道题就做完了，作为引例其实就是高中数学难度，只是涉及到概率还没有$DP$，画画图还是可以轻易完成的。

Collecting Bugs

问题描述：一个软件有 $s(0 \le s \le 1000)$ 个子系统，会产生 $n(0 \le n \le 1000)$ 种 $bug$。某人一条发现一个 $bug$。每个 $bug$ 属于一个子系统，属于一个分类，且每个 $bug$ 属于某个子系统的概率是 $\frac{1}{s}$，属于某个分类的概率是 $\frac{1}{n}$。求发现了 $n$ 种 $bug$，且每个子系统都发现了 $bug$ 的天数期望。

我们还是先来看样例 Input:1 2 Output:3.00000。这道题其实看起来很玄乎，玄乎就玄乎在这个天数有可能是无穷的，就可能这个人运气很差，某一个类别或者某一个子系统就一直不出现，虽然概率很小但还是存在的。正常来说我们应该是计算 $1*P_{1天完成}+2*P_{2天完成}+3*P_{3天完成}+……$ 但是一旦我们这么做由于天数有可能到无穷就是一个无穷级数的累加，就可能要积分和无穷级数之类的。我们不推荐在算法竞赛中主动使用积分，用也大体是用数值计算的方法。

我们这里可以发挥动态规划一个非常好的优点，我们虽然没有算出来但是我们可以把它当成已经算出来了。我们设 $f[i][j]$ 表示现在已近找到的 $bug$ 有 $i$ 种，属于 $j$ 个系统，找到剩下的 $bug$ 所需要的期望天数。那么我们每天有四种情况：

• 发现一个$bug$属于已经有的 $i$ 个分类和 $j$ 个系统： $\frac{i}{n} * \frac{j}{s} * (f[i][j] + 1)$；
• 发现一个$bug$属于已有的分类，不属于已有的系统：$\frac{i}{n} * (1 - \frac{j}{s}) * (f[i][j + 1] + 1)$；
• 发现一个$bug$不属于已有的分类，属于已有的系统：$(1 - \frac{i}{n}) * \frac{j}{s} * (f[i + 1][j] + 1)$；
• 发现一个$bug$不属于已有的分类，也不属于已有的系统：$(1 - \frac{i}{n}) * (1 - \frac{j}{s}) * (f[i+1][j+1] + 1)$。

我们把上面的式子写到一起： $$
f[i][j] = (\frac{i}{n} * \frac{j}{s} * (f[i][j] + 1)) + (\frac{i}{n} * (1 - \frac{j}{s}) * (f[i][j + 1] + 1)) + ((1 - \frac{i}{n}) * \frac{j}{s} * (f[i + 1][j] + 1)) + ((1 - \frac{i}{n}) * (1 - \frac{j}{s}) * (f[i+1][j+1] + 1))
$$。然后我们发现左右都有 $f[i][j]$，我们就可以把右边的 $f[i][j]$ 移到左边，这样右边的东西就与 $f[i][j]$ 没关系的。而我们的起点是 $f[n][s] = 0$，我们从大到小推导，所以在计算 $f[i][j]$ 时，右边的 $f[i + 1][j],f[i][j + 1],f[i + 1][j + 1]$ 都已经计算完了故我们可以顺利计算。 我们最后的答案就是 $f[0][0]$。

我们这道题其实就利用了动态规划的虽然没算出来但我们可以设出来找找窥看有没有什么递推关系，如果无后效性就可以和这题一样直接递推，有后效性可能就要变成若干个方程进行高斯消元。这题倒着循环或者记忆化搜索都可以。

带富翁

问题描述：小明在玩一款带富翁游戏，这个游戏具体来说就是有 $n$ 个奖励点，每个奖励点有一定的奖励分。一开始他站在位置 $1$。每次他都会扔一个有 $6$ 面的骰子，如果扔到了 $x$，并且小明现在站在 $i$ 这个位置，小明就会向前进 $x$ 步到达 $i+x$ 这个位置。
如果小明扔出了 $x$ 并且 $i+x$ 已经大于了$n$，那么小明就会重新扔，直到 $i+x$ 在合适的位置。小明最后如果到达了 $n$ 号位置，那么小明就会结束游戏，现在小明想知道自己期望的得分是多少。

概率$DP$和我们之前做的动态规划的最大不同就是之前的动态规划是知道多少布就结束了但是概率$DP$特别是涉及到期望往往我们是不知道要走多少步的。所以我们的关注点就转移到达到某种境地的一个期望而不是走多少步的期望。

比如在这道题中，我们设 $f[i]$ 表示从 $i$ 走到 $n$ 获得的金子的期望。那如果 $i + 6 \le n$ 即不会走出去，那 $f[i] = a[i] + \sum_{k \in [1, 6]}(\frac{1}{6} * f[i + k])$；但如果 $i + 6 > n$ 那么我们就有 $f[i] = a[i] + \sum_{k \in [1, x],i + x = n}(\frac{1}{x} * f[i + k])$。

这样这道题就比较简单了，直接递推就可以了。但如果我们对题目进行一个变型，我们的骰子可以投出 $0-6$，也就是有可能回到自己再吃一波分，这时我们就要仿照第一题将 $f[i]$ 移到一边，再进行后面的递推。

骰子游戏

问题描述：吉吉国王正在玩一款手游，这个手游的规则非常简单。一开始你会得到三个筛子，三个骰子分别有 $k_1, k_2,k_3$ 面，也就是说分别可以扔出 $[1, k_1], [1, k_2], [1, k_3]$ 之间数 $(1 \le k_i \le 6)$。
一开始的分数为 $0$，每次扔骰子都会扔出 $x,y,z$ 三个数，但是这个游戏的特别之处在于每次开局都会给定三个数 $a,b,c$，如果满足 $x = a, y = b, z = c$，那么你的分数就会清零，否则你的分数就会加上 $x + y + z$。现在吉吉国王想知道期望需要扔多少次才能使得他的分数大于$n(0 \le n \le 500)$。

首先由于 $1 \le k_i \le 6$ 非常小，我们可以先枚举出三个骰子的点数，预处理出 $p[i]$ 这个数组。其中 $p[k]$ 表示投掷出 $k$ 分的概率，特殊地 $p[0]$ 表示回到 $0$ 的概率。然后我们设 $f[i]$ 为到达 $i$ 分时到达目标状态的期望步数，则 $f[i] = \sum_{k>0}(p[k] * f[i + k]) + f[0] * p[0] + 1$，并且对于 $i > n$ 初始化 $f[i] = 0$。然后由于我们是从大到小推的，但是右边却有一个 $f[0]$ 也就是我们最后的答案，一定是一个常数。所以我们设 $f[i] = A[i] * f[0] + b[i]$，带入上述方程右边得到：$$f[i] = \sum_{k>0}(p[k] * (A[i + k] * f[0] + B[i + k])) + f[0] * p[0] + 1 = (\sum_{k>0}(p[k] * A[i + k]) + p[0]) * f[0] + \sum_{k>0}(p[k] * B[i + k]) + 1$$。那么 $A[i] = \sum_{k>0}(p[k] * A[i + k]) + p[0]$， $B[i] = \sum_{k>0}(p[k] * B[i + k]) + 1$。

那就很简单了，我们知道 $f[n] = 0$，而 $A[n] = B[n] = 0$，所以我们可以从后往前递推出我们的 $A[0]$ 和 $B[0]$，那么由 $f[0] = A[0] * f[0] + B[0]$ 知道 $f[0] = \frac{B[0]}{(1 - A[0])}$。

这样我们就完成这道题了。其实这种方法是很常见的，但如果确实推不出来还有更加通用的方法，就是直接上高斯消元解决，只不过时间上需要多斟酌一下。

食堂

问题描述：吉吉国王偶尔会回想起自己的高中时代。在吉吉国王的高中时代，下课后冲向食堂是每个学生的基本操作，但是总得有人失败，为什么不能是我，实际上吉吉国王在打饭这件事上也是失败过很多次，比如没带饭卡，走错窗口，甚至食堂关门。
吉吉国王的高中食堂排队可以看成一个长度为 $n$ 的队列，一开始吉吉国王站在 $m$ 这个位置上，一般来说，窗口前的第一个人在打饭的时候会发生四种情况。
第一种情况是打饭的时候窗口没人，这个时候要等待一会儿，发生的概率是 $p_1$。
第二种情况是发现自己没带饭卡，这个时候就要回去拿饭卡并且排到了队列的末尾，发生的概率是 $p_2$​。（这里认为每个人只有在即将打饭的时候才会去摸饭卡，只有这时才有发现自己没带饭卡的机会。）
第三种情况是打饭成功，这个时候队列的长度减一，发生的概率是 $p_3$​。
第四种情况是食堂关门，这个时候大家都不能打饭了，发生的概率是 $p_4$​。
吉吉国王老倒霉蛋了，经常在食堂关门的时候排在队伍的前面，因此他想知道这样的事件发生的概率。现在你需要告诉吉吉国王在食堂关门时他排在队伍的前 $k$ 位的概率。
其中 $1 \le k \le m \le n≤2000,0 \le p_1, p_2, p_3, p_4 \le 1, p_1 + p_2 + p_3 + p_4 = 1$ 。

我们设 $f[i][j]$ 表示 $i$ 个人排队，国王排在第 $j(j \le i)$ 个位置，达到目标状态也就是食堂关门时他排在队伍的前 $k$ 位的概率的概率。那么我们要求的就是 $f[n][m]$。我们下面考虑如何转移：

• $j == 1$，也就是我们的国王就站在队首。那可能导致达到目标状态也就是食堂关门时他排在队伍的前 $k$ 位就有三种情况，一是进入等待，二是忘记带饭卡要回去拿然后重新排队，三是这时饭堂直接关门了，也就是$p_1 * f[i][1] + p_2 * f[i][i] + p_4$；
• $2 \le j \le k$，也就是当前食堂关门国王也能到达目标状态，所以有四种情况，一是第一个人等待那么国王也要等待，二是队首忘记带饭卡那么总人数不变但是国王排位减一，三是队首顺利打饭那么总人数和排位都减一，四就是饭堂直接关门，也就是 $p_1 * f[i][j] + p_2 * f[i][j - 1] + p_3 * f[i - 1][j - 1] + p_4$；
• $k < j \le i$，那这时食堂关门不能到达目标状态，所以有三种情况，一还是第一个人等待那么国王也要等待，二还是队首忘记带饭卡那么总人数不变但是国王排位减一，三还是队首顺利打饭那么总人数和排位都减一，然后直接饭堂关门不能到达目标，所以最后没有 $+p_4$，也就是：$p_1 * f[i][j] + p_2 * f[i][j - 1] + p_3 * f[i - 1][j - 1]$。

我们还是把 $f[i][j]$ 都移动到左边，用递推的方法或者记忆化的方法，最后求出的 $f[n][m]$ 就是答案。

结语

在这篇$BLOG$中，通过一些没有一定要使用高斯消元的有意思的概率题我们一共学习了概率$DP$。其实在很多类似的题目当中都是不一定要用甚至由于范围限制不能用高斯消元的。动态规划嘛关键还在做题，后面我也会分享一些有意思的其他动态规划题目。最后希望你喜欢这篇$BLOG$！