在上学期的机器学习课程中,我们探究了多种方式的图片压缩方法,取得了还不错的成果,下面我们就来一同看看吧。
选题背景
屏幕的分辨率越来越高,从480P到4K,人们在享受着更加清晰的画面的同时,也给传输速率和存储空间带来了巨大的挑战。一般来说,越清晰的图片,所占的空间就越大。一张大图片,有着很高的清晰度,可以给人很好的观感,这无疑是好的,现在也有足够的技术处理大图片。但是,某些地方存在大图片的滥用,明明展示图片的框框就那么大,即使比较小的图片也已经足够清晰了,若继续增加图片的大小,不仅不会增加清晰度,反而会浪费空间。这时,就要对图片进行压缩,而压缩就意味着图片质量会下降。但是,图片的质量和大小并不是简单的线性关系,压缩图片的方式有多种,每一种都会对图片产生不同的影响。究竟哪一种压缩方式可以在节省更多空间的同时,更大程度地保持图片的原汁原味,就是我们想要探寻的内容。
开发环境
Anaconda3
Python 3.8
Numpy 1.19.4
Matplotlib 3.2.2
Pillow 7.2.0
Scipy 1.5.4
Scikit-learn 0.24.0
数据源及数据处理
为了更好地探究图片压缩的效果,我们选取了一张中山大学的校园风景图片进行压缩实验,该照片经过分辨率高,色彩鲜艳的,大小为10.00MB。下面的实验我们都会使用这幅图片,展示我们的压缩算法在极大的大小和极为丰富的色彩的情况下对于图像压缩的效果。下为该图片:

模型设计
针对图像压缩这个问题,我们设计了五种类型的模型,其中有两种创新性地结合了多种图像压缩方式,也达到了长江后浪推前浪一代更比一代强的效果。下面我们就来一种一种方法来看吧!
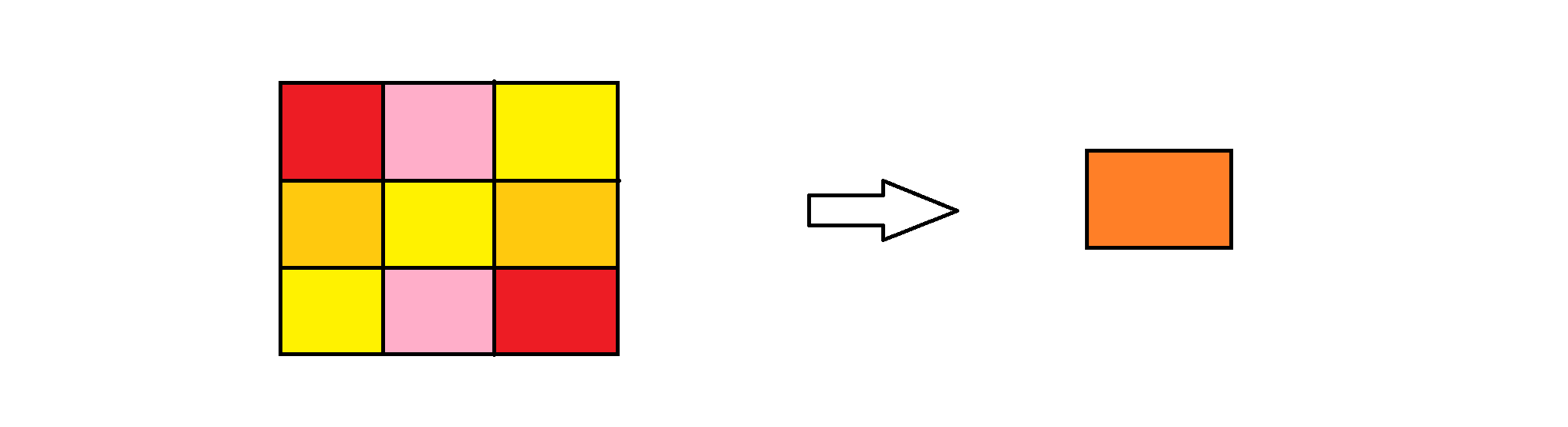
(1) 平均像素的直接压缩法
说到压缩图像,可能很多人第一反应就是直接对于图片像素大小进行压缩,就是我们可以每33或者44个像素的RGB值取一个平均值作为1个像素的RGB值。这个过程是不是非常眼熟?没错就和我们神经网络当中的池化有着异曲同工之妙。在这样操作下,我们的图片大小可以直线下降,并且在图片像素差别不大的情况下可以取得比较好的压缩效果:
(2) SVD图片压缩法
在我们大一学习线性代数的时候,老师就就告诉过我们奇异值分解(SVD)在我们日后的学习和生活中可以运用在图像压缩上。那它的原理是什么呢?首先我们先了解一下对于方阵而言的特征向量和特征值分解。
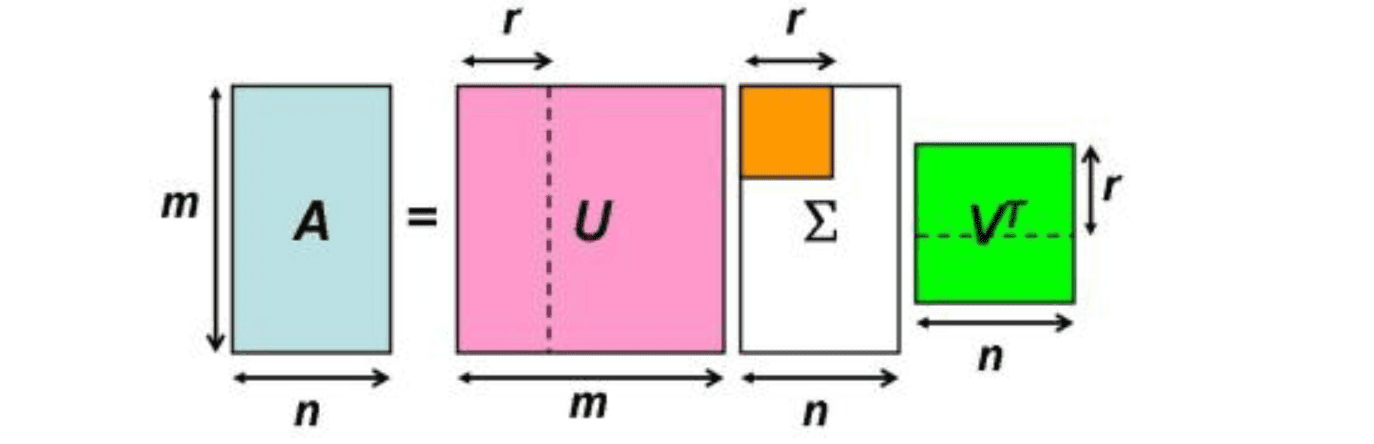
如果一个向量v是矩阵A的特征向量,则一定可以表示为Av = Aλ,其中λ被称为特征向量v对应的特征值。而特征值分解指的是,我们讲方阵A分解为A=Q ∑ Q^-1。其中Q是矩阵A的特征向量组成的矩阵,∑则是一个对角矩阵,对角线上的每一个点都是一个特征值。而特征值和特征向量可以非常好地反应矩阵的一些性质,所以我们在一定程度上可以用Q和∑来反应我们矩阵的特点。反应在图像上我们就可以用更少的有代表性的像素来反应我们整张图的性质。
但是我们的图片怎么会正正好好是个方阵呢?而且每个像素点还有RGB值三维的属性。所以我们针对普通矩阵,也有类似的方法,那就是特征值分解(SVD)。对于任意的矩阵,我们可以尝试把他们分解为A = U ∑ V,我们再用这三个矩阵代替我们上面的∑和Q来反应我们的矩阵来达到我们图片压缩的最终目的。
(3) Kmeans图片压缩法
Kmeans作为聚类算法的一种,算的上是我在机器学习基础这门课当中学到的最喜欢的算法了。运用简单的迭代,我们就能找到聚类点的中心,真的是非常的巧妙。下面就请允许我为您再次介绍一下Kmeans算法的原理和大致流程。
当运行K-Means算法时,我们开始时需要初始化K个聚类中心,K值一般要比训练样本的数量 m 小,因为如果运行一个 K均值聚类中心数量等于或者大于样本数的K-Means算法会很奇怪。人们通常初始化K-Means算法聚类的方法是随机挑选K个训练样本,将它们作为聚类中心设定μ1 到 μk。
让我们来看一个具体的例子,对于下面这样一组数据点:
假设 K = 2, 那么为了初始化聚类中心我们要做的是随机挑选两个个样本作为初始化的聚类中心:
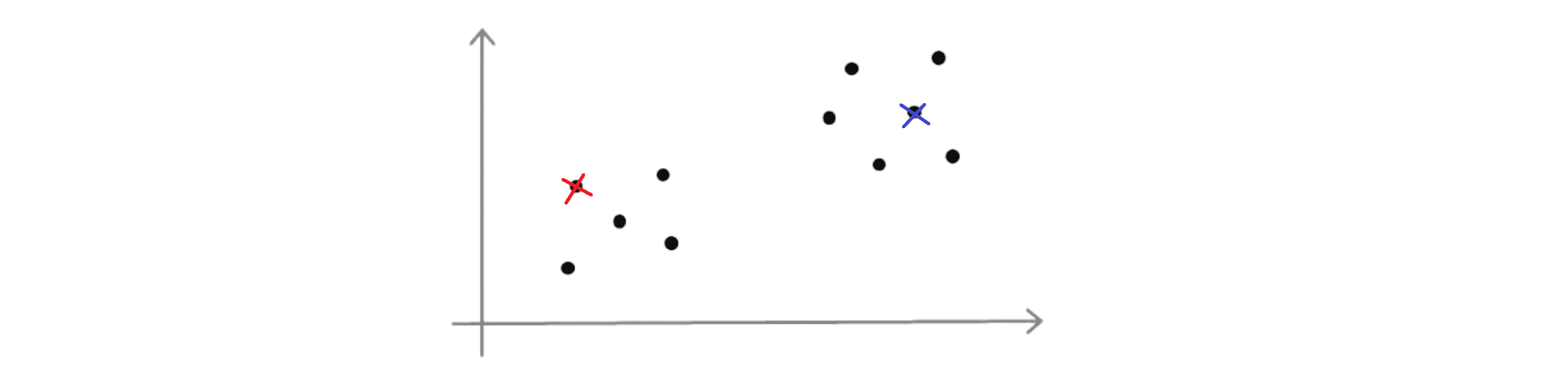
刚刚我们画的看上去是相当不错的一个例子,但是有时候我们可能不会那么幸运也许我最后会挑选下面这两个聚类中心:
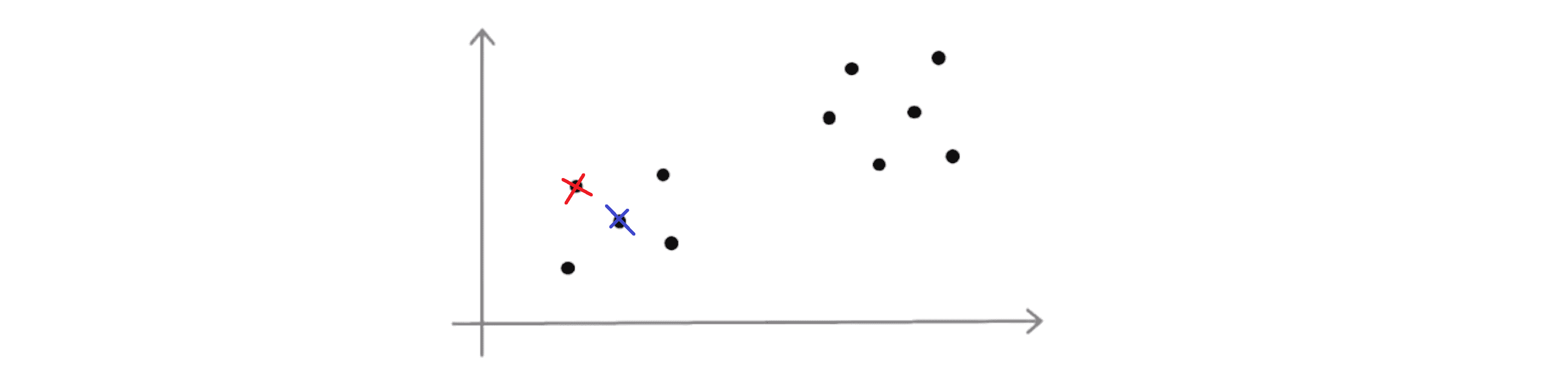
这就是如何随机初始化聚类中心。也许通过上面的两幅图,你已经猜到采用K-Means算法进行聚类最终可能会得到不同的结果。其最终结果往往取决于聚类簇的初始化方法,因此也就取决于随机的初始化。K-Means算法最后可能得到不同的结果,尤其是如果K-Means算法最后收敛在局部最优的时候。所以在我们库的内部实现当中通常会多次取点进行该算法来得到一个比较好的结果。
那对于我们的图片来说我们要对什么进行聚类呢?没错就是颜色。用心观察我们周围的世界你就会发现其实很多物品它本身的颜色差异不会很大,那通过聚类我们选取几种颜色,就能大致表现出物品的颜色属性,这样也能大大减少我们图片对于颜色通道这一部分空间的占用,以达到我们压缩图片的目的。
(4) Kmeans+SVD图片压缩法
我们理解了SVD和Kmeans的操作原理,其实通过对上面三个模型的实验结果观察我们就会发现,SVD最大的问题就是由于颜色太杂容易出现类似于白噪声一样的噪点,所以我们组经过讨论决定尝试先通过Kmeans算法对颜色数量进行降低换句话说让整个图片的颜色变得更纯,再进行SVD这样的出来的图片理论上应该会比单独使用这两种方法会更好,在后面的实验结果当中我也会进行相应的论述。
(5) 上述方法+平均像素压缩法
其实运用了这么多种方法我们会发现其实平均像素压缩法真的可以算的上是万金油,任何算法做完以后都能丢进去再平均像素压缩一下,以在保持大体质量存在的前提下增加我们的压缩比。
模型实现
讲了这么多原理,下面我们一种一种方法来进行实现。
(1)平均像素的直接压缩法
通过查阅资料,我发现网上大部分代码写的很复杂,都是这个矩阵那个矩阵运算的,对于我们初学者来说非常不友好。但我们写的这一部分的代码较为简单,我们的大致思想就是先确定整幅图的最终像素大小,然后我们用Pillow自带的功能将我们的图片压缩到我们确定好的大小,其中压缩的方法就是我们的平均像素压缩法。所以我们的代码就如下:
from PIL import Image
img = Image.open('C:\\Users\84293\Desktop\Python\QwQ\SYSU.jpg')
w,h = img.size
for i in range (2, 11):
ww,hh = round(w / i),round(h / i)
img = img.resize((ww, hh), Image.ANTIALIAS)
img.save('C:\\Users\84293\Desktop\Python\QwQ\%.1f.jpg'%i, optimize=True, quality=85)(2)SVD图片压缩法
在之前的学习中,我曾经尝试过用C++去实现我们的SVD,但是确实非常复杂细节非常多。但是现在在python当中,依托于numpy库,求解奇异值就变得非常的简单,再加上我们的matplotlib库,我们就能非常方便地将我们计算好的矩阵以图片的形式输出啦。当然运用matplotlib库有一个地方是很多网上的博客都没有注意到的地方,就是matplotlib的默认输出是带白边和坐标轴的,所以我们在输出图片之前我们要将图片的坐标轴给去掉白边给去掉,要不然会增加无意义的像素降低我们压缩的呈现效果。所以总的代码就如下所示:
import numpy as np
import matplotlib.pyplot as plt
import os
im = plt.imread('C:\\Users\84293\Desktop\Python\SVD\SYSU.jpg') ##导入图片
# print('origin_image shape:', im.shape)
# img = np.zeros(shape=im.shape, dtype='uint8')
for r in range(1,361, 20):
svd_image = []
for ch in range(3):
im_ch = im[:,:,ch]
U,D,VT = np.linalg.svd(im_ch)
imx = np.matmul(np.matmul(U[:,:r],np.diag(D[:r])),VT[:r,:])
svd_image.append(imx.astype('uint8'))
##SVD
img = np.stack((svd_image[0], svd_image[1], svd_image[2]), 2)
plt.imshow(img)
plt.axis('off')##不显示坐标轴
plt.savefig('C:\\Users\84293\Desktop\Python\SVD\%02d.jpg'%r, bbox_inches='tight', pad_inches=0)
##去白边!!!!(3)Kmeans图片压缩法
如果我们使用其他语言来实现Kmeans,我们多半就要写递归迭代,但是python好啊,依托于sklearn里的MiniBatchKMeans,我们只需要设置参数和投喂数据就可以了。所以代码就如下所示:
import numpy as np
from sklearn.datasets import load_sample_image
from sklearn.cluster import KMeans, MiniBatchKMeans
from PIL import Image
import matplotlib.pyplot as plt
#读取原始图像数据,并转换为三维数组
imOrigin = Image.open('C:\\Users\84293\Desktop\Python\KMeans\SYSU.jpg')
dataOrigin = np.array(imOrigin)
#进行变形
data = dataOrigin.reshape(-1, 3)
# 使用KMeans把所有像素的颜色划分为r类
for r in range(2, 20):
kmeansPredicter = MiniBatchKMeans(n_clusters = r, batch_size = 20)
kmeansPredicter.fit(data)
#进行颜色的替换
temp = kmeansPredicter.predict(data)
dataNew = kmeansPredicter.cluster_centers_[temp]
dataNew.shape = dataOrigin.shape
dataNew = dataNew / 255
plt.imshow(dataNew)
plt.axis('off')##不显示坐标轴
plt.savefig('C:\\Users\84293\Desktop\Python\Kmeans\%02d.jpg'%r, bbox_inches='tight', pad_inches=0)(4)Kmeans+SVD图片压缩法
这一部分我们只需要将上两部分的代码整合起来或者不整合直接将Kmeans处理好的图像再丢给SVD进行处理就可以了。由于篇幅的原因,这里就不展示组合后的代码了,感兴趣的同学只需要下载我们上两部分的代码按照先进行Kmeans再进行SVD的顺序进行就好啦。
(5)上述方法+平均像素压缩法
和第四种方法一样,这一种方法本质上也是将上面的代码在处理之后再丢到第一部分的代码再次进行压缩就可以了,这里就不过多赘述了,我们直接进行下一步模型的对比。
模型评测
在这一部分模型评测当中,我主要分为两大部分,一个是模型内的评测,另一个是模型之间的对比评测,我会穿插着进行讲解。
首先是平均像素压缩法法,我们选取了压缩了2~10倍的图片,其实乍一眼看上去好像图片之间都没什么区别:

但是点开图片就能发现,压缩两倍和压缩十倍的效果还是有着非常巨大的区别的:
压缩两倍:

压缩十倍:

我们通过对比发现其实在四倍以前不放大图片的话我们的肉眼是观察不出什么区别的,但是此时图片大小已经从10M变成了255k,可以说是非常万金油的一种压缩方式了。
接着是SVD压缩法,我们这里选取的是前1~341个特征值进行压缩,其差异比之前的平均像素压缩法明显的多:
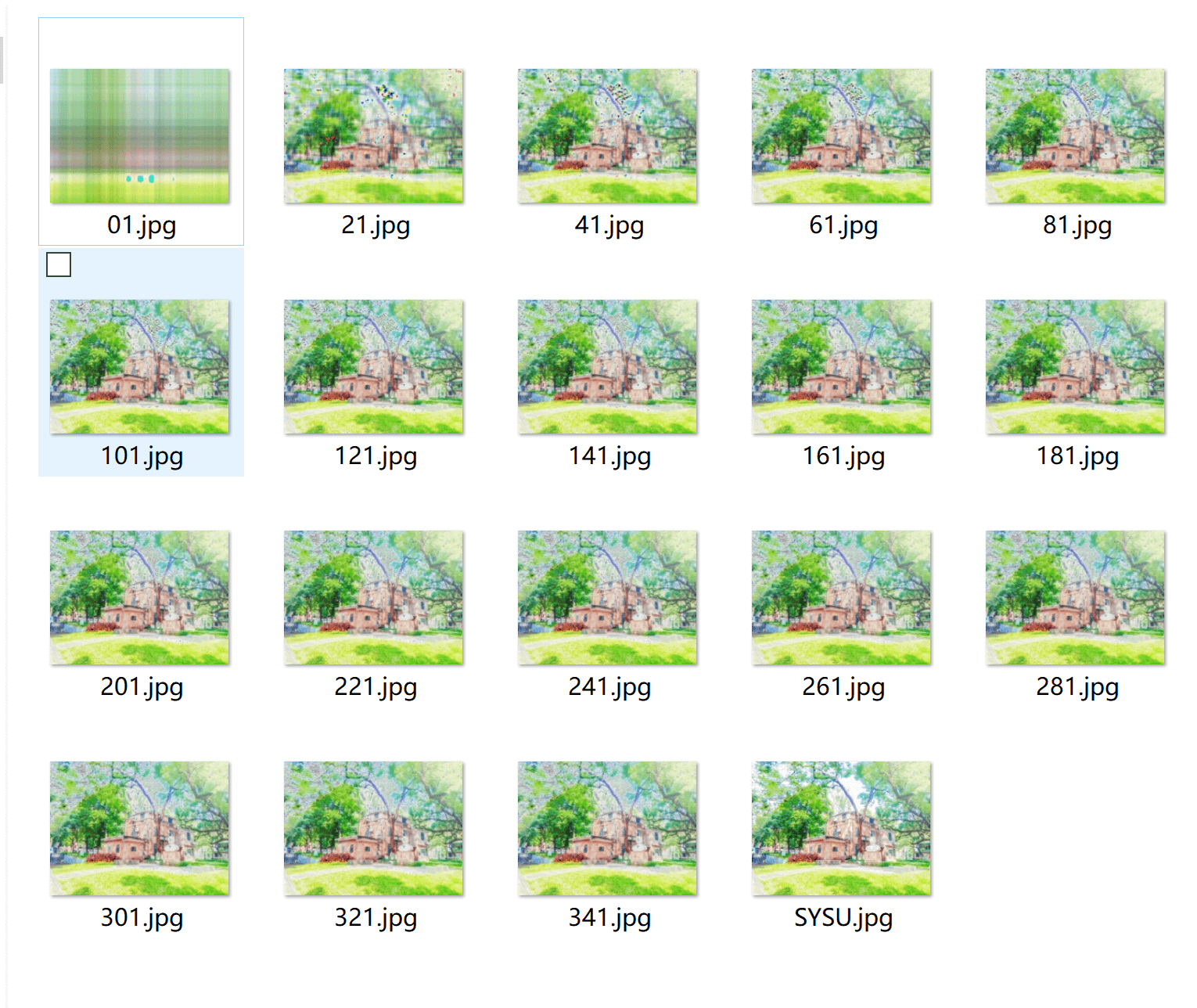
在300以前,图片都存在着相当多的噪点,基本属于不可用状态,比如下面是200的情况:

340的情况:

当然由于时间的问题我们没有尝试更大维度的SVD,在今后的时间中,我们必定填这个缺憾,这还远不是我们SVD的极限。
那现在就让我们来看看我们的Kmeans算法吧,这个算法非常有意思,通过上面的算法描述你应该都知道了,我们这次压缩的不是像素而是颜色,当然这样可能也有着钝化的作用,我们依次生成了剩下2~100种颜色的图片:

这个最后剩下两种颜色真的可以说是别有一番风味,有小学作业本的感觉了:

我们通过观察可以发现在20种颜色的时候,我们的图片就已经基本成型了,而且此时的大小也只有42.1K。况且这还只是针对这种颜色比较复杂的图片,要是换成颜色比较单一的图片比如天空啊大海啊什么的我觉得Kmeans算法还能发挥更好的效果,下面是二十种颜色的情况:

最后让我们来看看我们的创新算法,Kmeans+SVD。其实刚开始我对这种方法并不抱有很大的期望,因为SVD压缩图片后产生的噪点真的是太难消除了。但Kmeans将图片颜色这么一压缩,SVD出来的效果确实很不错,我们先来看看SVD在没有进行Kmeans算法时200维跑出来的结果:

树叶之间和天空基本上都是噪点。但当我们用Kmeans将图片压缩到20、50、80、100种颜色时我们发现,在保证颜色丰富度的情况下,这些马赛克一样的噪点消失了!!留下的图片更加清纯更加有感觉,下面依次是20、50、80、100种颜色:




取得了较好的效果。
创新点
在这次实验当中我们的创新点主要体现在两个方面:
一是对于我们已有的平均像素压缩,SVD和Kmeans算法,我们改良了算法进程,优化了部分细节(比如去除白边),增加了多组的输出加强对比,并且更改了一些错误。
二是我们创新性地针对SVD产生的压缩图片噪点过多的情况,提出了先进行一遍Kmeans算法再进行一遍SVD算法,通过上述产生的输出我们可以发现,取得了非常好的效果,有效地解决了SVD的痛点并且将我们产生的压缩图片体积进一步减小。
结果分析及结论
通过上述实验结果,我们可以对这几种算法进行分析比较。首先是像素平均压缩算法,这应该是最值得尝试的压缩算法了,犹如万金油一般的存在可以用在各种场合。Kmeans算法就不太挑图片,能在保持图像表现的情况下将我们原图片压缩至一个非常小的水准我个人认为非常适合在日后进行神经网络之前的数据预处理。而我们的SVD不太适合直接使用,容易产生较多噪点影响观感,我们建议使用我们的Kmeans+SVD的组合套餐,各取所长达到一个更好的效果。
我认为这次的实验时非常有意义的,在检验了我们这一学期掌握的知识以外,还留给了我们很多的思考和精进的空间。在接下来的学习中,我们也打算尝试使用神经网络进行图像压缩也期待他能产生不错的效果。
参考文献
1.https://blog.csdn.net/zhongkejingwang/article/details/43053513