这几天可能都会做各地省选题，所以这段时间就先放下新算法的讲解，重点讲解这些经典套题，那么几天就让我们走进SCOI 2006 DAY 1的奇幻旅程吧！

T1 zh_tree

题目描述：

Description

张老师根据自己工作的需要，设计了一种特殊的二叉搜索树。他把这种二叉树起名为zh_tree，对于具有n个结点的zh_tree，其中序遍历恰好为(1，2，3，…，n)，其中数字1，2，3，…，n 是每个结点的编号。n个结点恰好对应于一组学术论文中出现的n个不同的单词。第j个单词在该组论文中出现的次数记为dj，例如，d2=10表示第2个结点所对应的单词在该组论文中出现了10次。设该组论文中出现的单词总数为S，显然，S=d1+d2+…+dn。记fj=dj/S为第j个单词在该组论文中出现的概率（频率）。 张老师把根结点深度规定为0，如果第j个结点的深度为r，则访问该结点的代价hj为hj=k(r+1)+c，其中k，c为已知的不超过100的正常数。 则zh_tree是满足以下条件的一棵二叉树：它使 h1f1+h2f2+…+hnfn 达到最小。我们称上式为访问zh_tree的平均代价。 请你根据已知数据为张老师设计一棵zh_tree。
Input

第1行：3个用空格隔开的正数： n k c 其中n<30，为整数，k，c为不超过100的正实数。 第2行：n个用空格隔开的正整数，为每个单词出现的次数(次数<200)。
Output

第1行：(5分)一个正实数，保留3位小数，为访问Zh_tree的最小平均代价。 第2行：（5分）n个用空格隔开的整数，为该树的前序遍历。一般地，作为最优解的前序遍历不一定唯一，只输出一个解。

Sample Input
4 2 3.5
20 30 50 20

Sample Output
7.000

AC解法：

这道题字里行间都透露出一种DP的芳香，没错，这就是一道很经典的区间DP（其实也可以说是记忆化搜索）。

我们定义数组dp【l】【r】【k】表示区间l，r的根节点在深度k时的最小代价；所以很显然的就可以分为三种情况：

1.l为这一层层的根节点，【i+1，r】的根节点在k+1层；
2.r为这一层的根节点，【i，r-1】的根节点在k+1层；
3.在（l，r）中有一个点i为根节点，【l，i-1】和【i+1，r】的根节点在k+1层

所以动态规划方程就很显然了：

double maxx=1000000000.0000;
        maxx=my_min(maxx,find(l+1,r,dep+1)+f[l]*(k*dep+c));
        maxx=my_min(maxx,find(l,r-1,dep+1)+f[r]*(k*dep+c));
        for(int i=l+1;i<r;i++)
        {
            maxx=my_min(maxx,find(l,i-1,dep+1)+find(i+1,r,dep+1)+f[i]*(k*dep+c));
        }
        dp[l][r][dep]=maxx;

接下来我们只需要从（1，n，1）出发（dep从1开始是为了解决题目中r+1的问题），逐层DP，加以记忆化，就可以很轻松的在时限内完成这道题了。

程序部分：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
double f[110],dp[110][110][110],c,k;
int a[110],i,j,m,n,o,p,js,visit[110][110][110]={0},jl,tot;
double my_min(double x,double y)
{
    if(x<y)return(x);
    else return(y);
}
double find(int l,int r,int dep)
{
    if(visit[l][r][dep]==1)return(dp[l][r][dep]);
    visit[l][r][dep]=1;
    if(l==r)
    {
        dp[l][r][dep]=f[l]*(dep*k+c);
        return(dp[l][r][dep]);
    }
    else
    {
        double maxx=1000000000.0000;
        maxx=my_min(maxx,find(l+1,r,dep+1)+f[l]*(k*dep+c));
        maxx=my_min(maxx,find(l,r-1,dep+1)+f[r]*(k*dep+c));
        for(int i=l+1;i<r;i++)
        {
            maxx=my_min(maxx,find(l,i-1,dep+1)+find(i+1,r,dep+1)+f[i]*(k*dep+c));
        }
        dp[l][r][dep]=maxx;
        return(dp[l][r][dep]);
    }
}

int main()
{
    scanf("%d%lf%lf",&n,&k,&c);
    tot=0;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        tot=tot+a[i];
    }
    for(int i=1;i<=n;i++)f[i]=double(a[i])/double(tot);
    find(1,n,1);
    printf("%0.3lf",dp[1][n][1]);
    return 0;
}

T2 k进制集合的映射

题目描述：

AC解法：
这道题整个网站通过的人数少之又少，而且貌似找不到题解，这里就讲一下出题人的想法吧：

程序部分（不知道为什么不能直接贴，所以附上下载文件【后缀改为c就可用】）：

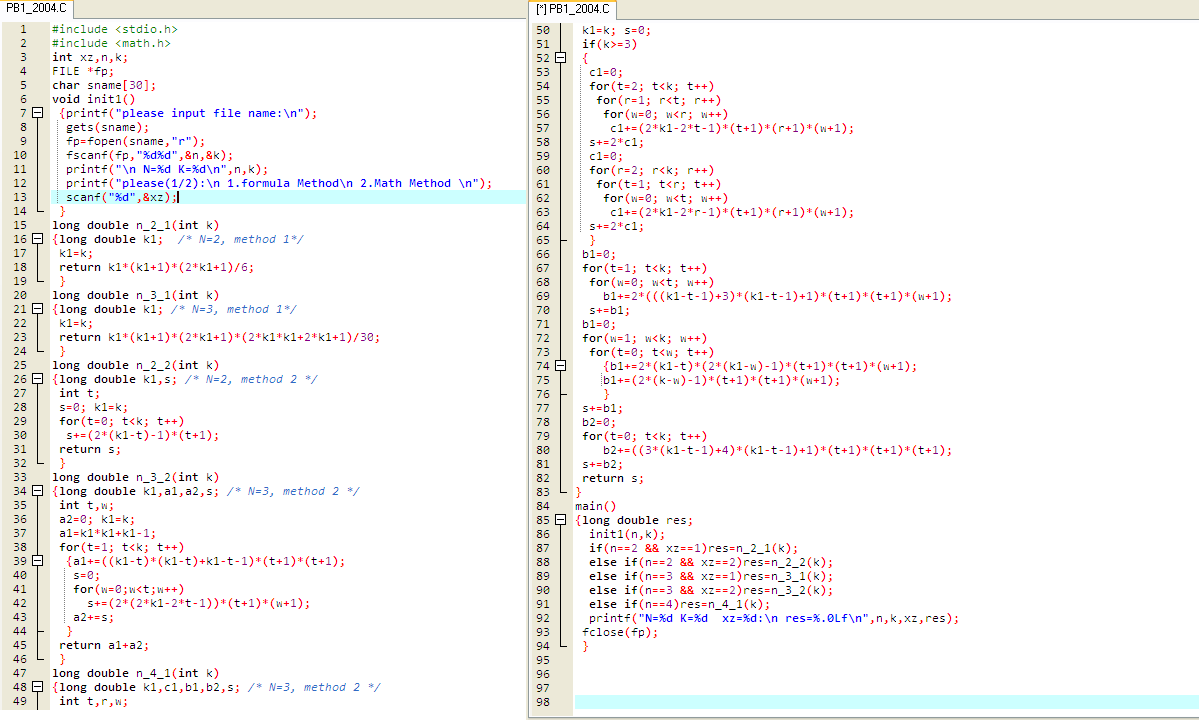
AC.txt

T3 整数划分

题目描述：

Description

从文件中读入一个正整数n（10≤n≤31000）。要求将n写成若干个正整数之和，并且使这些正整数的乘积最大。 例如，n=13，则当n表示为4+3+3+3（或2+2+3+3+3）时，乘积=108为最大。

Input
只有一个正整数： n （10≤n≤31000）

Output
第1行输出一个整数，为最大乘积的位数。 第2行输出最大乘积的前100位，如果不足100位，则按实际位数输出最大乘积。 （提示：在给定的范围内，最大乘积的位数不超过5000位）。

Sample Input
13

Sample Output
3
108

这道题就是很经典的结论题，可能很多人之前都想到过这个问题——将n写成若干个正整数之和，并且使这些正整数的乘积最大，那么怎么拆才最大呢？

没错，就是尽量拆成3相乘：那么为什么是这样呢？我们发现，当n=12时，可以写成2^6=64,3^4=81,4^3=64，然后我们就猜测这会不会是一个先递增再递减的图像?结果证明确实是这样。

所以我们就把n尽量拆成3，最后一个拆不了3就拆成2或者4，一定不要出现拆成1的情况！！！

由于要求输出前100位，再加之一共不超过5000位，裸的高精度乘法就好了。

程序部分：

#include<cstdio>
#include<cstdlib>
#include<algorithm>
using namespace std;
int i,j,k,m,n,o,p,js,jl;
int a[11000];
int matrix(int last,int x)
{
    for(int i=1;i<=last;i++)
    {
        a[i]=a[i]*x+a[i-1]/10;
        a[i-1]=a[i-1]%10;
    }
    if(a[last]>=10)
    {
        jl++;
        a[jl]=a[jl-1]/10;
        a[jl-1]=a[jl-1]%10;
    }
}
int main()
{
    scanf("%d",&n);
    a[1]=1;
    if(n<=4)
    {
        printf("1\n%d",n);
        exit (0);
    }
    jl=1;
    while(n>4)
    {
        n=n-3;
        matrix(jl,3);
    }
    matrix(jl,n);
    printf("%d\n",jl);
    if(jl<=100)for(int i=jl;i>=1;i--)printf("%d",a[i]);
    else for(int i=jl;i>=jl-99;i--)printf("%d",a[i]);
    return 0;
}

结语

对比2005年的SCOI DAY1,2006年难度得到了一定的提升，都是一些非常经典的题目，还是很值得一做的，希望你喜欢这篇题解。