好久没有更新计算几何的相关博客了。最近见到几道矩阵最大子矩形问题的题目，感觉可以拓展到计算几何上解决最大子矩形问题。下面就让我们逐一看看这些个问题吧。

矩阵最大子矩形问题

问题描述

在矩阵最大子矩形问题相关问题中，最出名的要数最大全零子矩形了。下面就让我们来看看问题描述。

题目大意：在一个给定的大小为a*b矩形网格中有n个障碍点，要找出网格内部不包含任何障碍点，且边界与坐标轴平行的最大子矩形。换句话说，我们在要一个大小为a*b的0,1方阵中找出其中最大的全0子矩阵：
010010
100010
001000
111000

这道题可以说是非常经典的一道题了，下面给出三种解决方法，其中第一种算法是在大部分题目中都会TLE的暴力算法，而第二种和第三种算法没有孰优孰劣只是分别来应付不同数据规模下的题目。

在这之前先让我们来明确几个概念：

• 有效子矩形：内部不包含障碍点的、轮廓与整个矩形平行或重合的子矩形。
• 极大子矩形：每条边都不能向外扩展的有效子矩形。
• 最大子矩形：所有有效子矩形中最大的一个（或多个）。

暴力枚举算法

看到这道题，我们很容易想到第一种算法，我们可以枚举这个子矩形的上下左右四条边界，很明显这个过程的时间复杂度是O((a*b)^2)。然后去看看枚举出来的子矩形是否里面全部都为0，这一过程我们有两种方法，一个是直接枚举子矩形里面的点看看有没有1的出现，这样的话就是O(a*b)；但有些比较聪明的同学应该早就想到我们可以用二维前缀和在单次O(1)的时间复杂度下查询到这个子矩形中1的个数，若个数为0则合法。所以加上前缀和优化这个算法总的时间复杂度就是O((a*b)^2)，这对于a*b比较大的情况是很容易超时的。

那我们的暴力算法就不能继续优化了吗？当然是可以的。我们可以枚举左右边界，对处在边界内的1按y排序，每两个相邻的点和左右边界组成一个矩形，就如同下面这样：

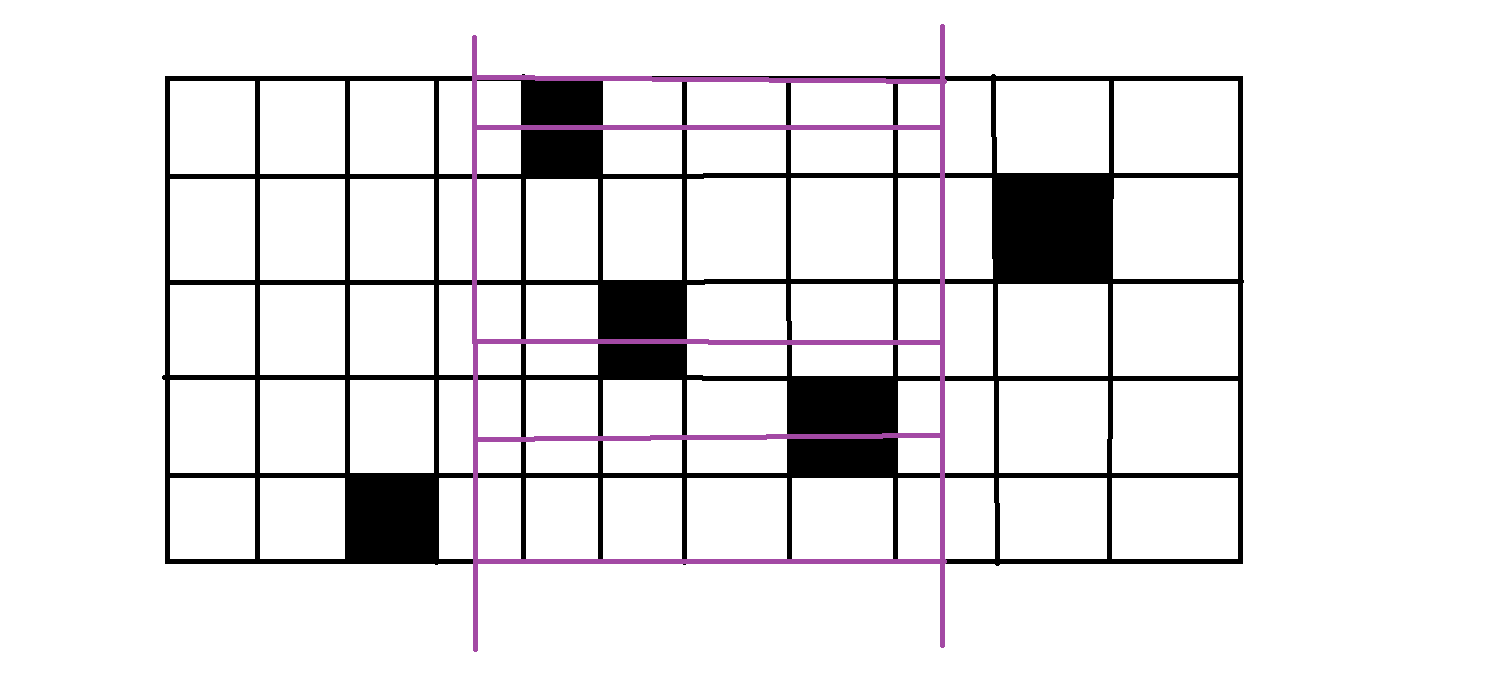
我们这次的复杂度变成了O（a*a*nlogn）但这种算法最坏情况下，也就是全部点都是黑点（1）的情况下，我们的复杂度还是会到达O((a*a)*(a*b)*log(a*b)),还是非常容易超时。

悬线法

算法原理

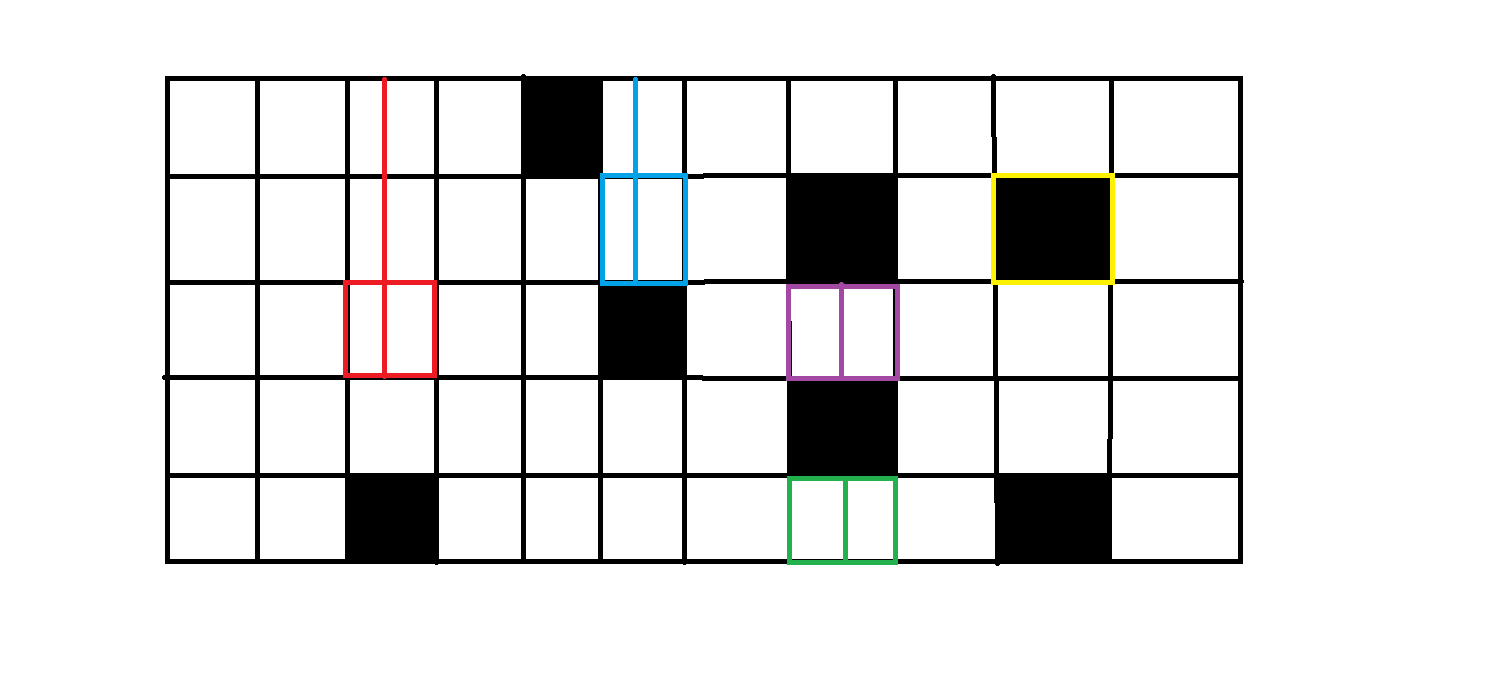
下面让我们来看一种时间复杂度只要O(a*b)的神奇算法——悬线法。首先什么是悬线呢？首先我们定义有效竖线是除了两个端点外，不覆盖任何黑点的竖直线段。接着我们就可以定义悬线为上端点覆盖了一个障碍点或达到整个矩形上端的有效竖线，下图中的红蓝紫黄都为悬线：

那悬线法的原理是什么呢？

我们知道对于任何一个极大子矩形，它的上边界上要么有一个障碍点，要么和整个矩形的上边界重合（要不然就能继续向上拓展）。那么如果把一个极大子矩形按列不同切割成多个与水平垂直的线段，则其中一定至少存在存在一条悬线。而且一条悬线通过尽可能地向左右移动恰好能得到一个子矩形（未必是极大子矩形，但只可能向下扩展）。

如果将一个悬线向左右两个方向尽可能移动所得到的有效子矩形称为这个悬线所对应的子矩形，那么所有悬线所对应的有效子矩形的集合一定包含了所有极大子矩形的合。每个悬线都与它底部的边一一对应，所以矩形中的每一个格点都对应了一个悬线。

那悬线法具体是怎么操作呢？待我一步一步为你道来。

首先对于每个点，我们都想象每个格子的下平面都有一条向上的悬线，它们一直延伸，直到碰到黑色的格子(代表是这个格子是1)，或者遇到边界：

比如上图中，红色边框的格子就有一条长度为3的红色悬线；蓝色边框的格子就有一条长度为2的蓝色悬线；紫色格子和绿色格子都各有一条长度为1的悬线；而黄色格子由于自身就是黑色格子所以悬线长度为0。

我们设从上往下第i行从左往右第j列的格子的向上悬线长度为h[i][j]，下面我们来考虑如何求解h[i][j]。很显然我们先分情况讨论，如果graph[i][j]==1也就是第i行第j列的格子是1也就是黑色的格子，那么显然悬线长度h[i][j] = 0；否则当graph[i][j]==0也就是第i行第j列的格子是0也就是白色的格子，第i行第j列的格子的悬线长度会是它正上方的悬线长度加一，所以我们这时有h[i][j] = h[i - 1][j] + 1。

同样低我们也可以想象每个格子的右平面都有一条向左的悬线，它们一直延伸，直到碰到黑色的格子(代表是这个格子是1)；左平面都有一条向左的悬线，它们一直延伸，直到碰到黑色的格子(代表是这个格子是1)。我们分别设设从上往下第i行从左往右第j列的格子的向左悬线长度为l[i][j]，向右的悬线长度为r[i][j]，我们也能用上面类似的方法求出l[i]j和r[i]j：

这样我们就求出了每个格子向上的悬线长度。接下来我们要考虑的是对于每条悬线我们能往左往右的最大拓展长度是什么。假如我们知道了最大向左拓展长度是l(包含自己本身[下图中蓝线])，向右拓展长度是r(包含自己本身[下图总绿线])，悬线长度是h，那么此时的答案就是(l + r - 1) * h。

由于向左向右的最大拓展长度是类似的，我们就着重来看看向左拓展的长度L[i][j]如何求解，假如对于下图这个位于第三列的橙色悬线：

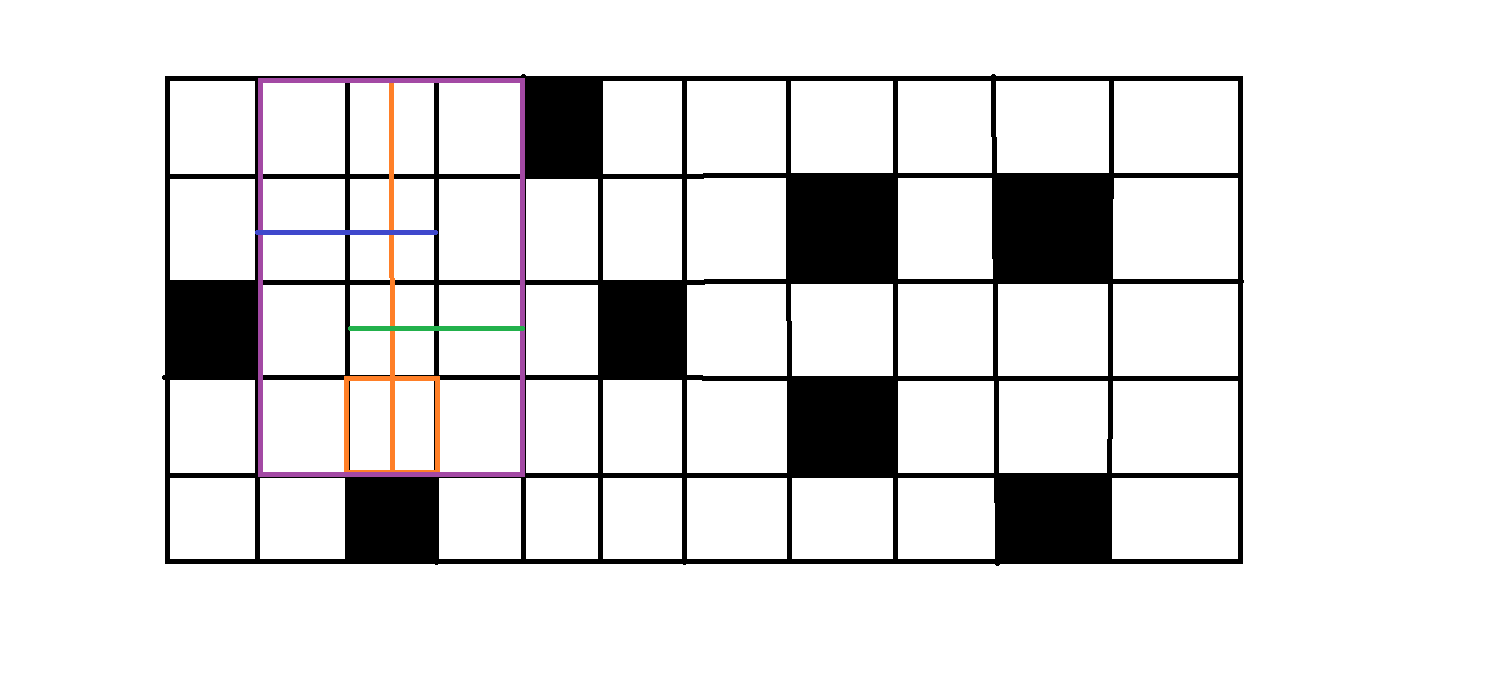
对于其第一行的点，能向左拓展的长度就是向左到达边界或者第一个黑色格点的长度所以显然就是L[1][3] = 3(包含自己本身)。而对于下面的L[i][3]，显然其悬线能向左拓展的最大长度就是自己上一个点的悬线能向左拓展的最大长度和自己这个点向左到达边界或者第一个黑色格点的长度取一个最小值。因为假设第i行第j列格子对应的悬线长度为n，能向左扩展L[i][j]。那么我们的前n-1格悬线肯定要能向左l[i][j]，第n格也要能向左扩展L[i][j]，换句话说L[i - 1][j]≥L[i][j] 且l[i][j]≥L[i][j]，而我们的L[i][j]想要最大，故L[i][j]=min(L[i-1][j], l[i][j])。同理我们也可以通过R[i][j]=min(R[i-1][j], r[i][j])求出R[i][j]。

所以最后我们就枚举i和j找到*max(h[i][j] (L[i][j] + R[i][j] - 1))**就是我们的答案啦。

算法实现

下面附上对于上述问题的悬线法代码模板：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
int graph[2200][2200];
int l[2200][2200] = {0}, r[2200][2200] = {0}, h[2200][2200] = {0};
int L[2200][2200] = {0}, R[2200][2200] = {0};
int n, m, ans = 0;
char s[10];

int main() {
    scanf("%d%d", &n, &m); //读入图的大小
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            scanf("%d", graph[i][j]);
        }
    } //读入图 

    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            if(graph[i][j] == 1) h[i][j] = 0;
            else h[i][j] = h[i - 1][j] + 1;
        }
    } //求向上悬线长度
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            if(graph[i][j] == 1) l[i][j] = 0;
            else l[i][j] = l[i][j - 1] + 1;
        }
    } //求向左悬线长度
    for(int i = 1; i <= n; i++) {
        for(int j = m; j >= 1; j--) {
            if(graph[i][j] == 1) r[i][j] = 0;
            else r[i][j] = r[i][j + 1] + 1;
        }
    } //求向右悬线长度

    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            if(h[i][j] > 1) {
                L[i][j] = min(L[i - 1][j], l[i][j]);
                R[i][j] = min(R[i - 1][j], r[i][j]);
            } //如果不是悬线开头 
            else {
                L[i][j] = l[i][j];
                R[i][j] = r[i][j];
            } //如果是悬线开头 

            ans = max(ans, h[i][j] * (L[i][j] + R[i][j] - 1));//更新答案 
        }
    }

    printf("%d", ans);
    return 0;
}

对应可解决题目：[Luogu P4147]玉蟾宫。

障碍点法

算法原理

在部分题目总，a和b可能比较大，但是n非常小，这时我们就可以使用时间复杂度为O(n^2)的障碍点法进行求解。

我们知道我们最后要求解的是最大子矩形，而最大子矩形一定是极大子矩形。换句话说我们只要找到所有极大子矩形，再从中取一个最大的就一定是答案了。

怎么找极大子矩形？根据极大子矩形的定义，我们可以得出极大子矩形的44条边一定覆盖障碍点（或边界）。为了方便讨论，对于横坐标是1~a，纵坐标为1~b的a行b列矩形，我们先将(0，0)(a+1，0)(0，b+1)(a+1，b+1)，4个顶点设为障碍点，这样的话极大子矩形的左右都一定是障碍点所在直线了。相当于下图这样：

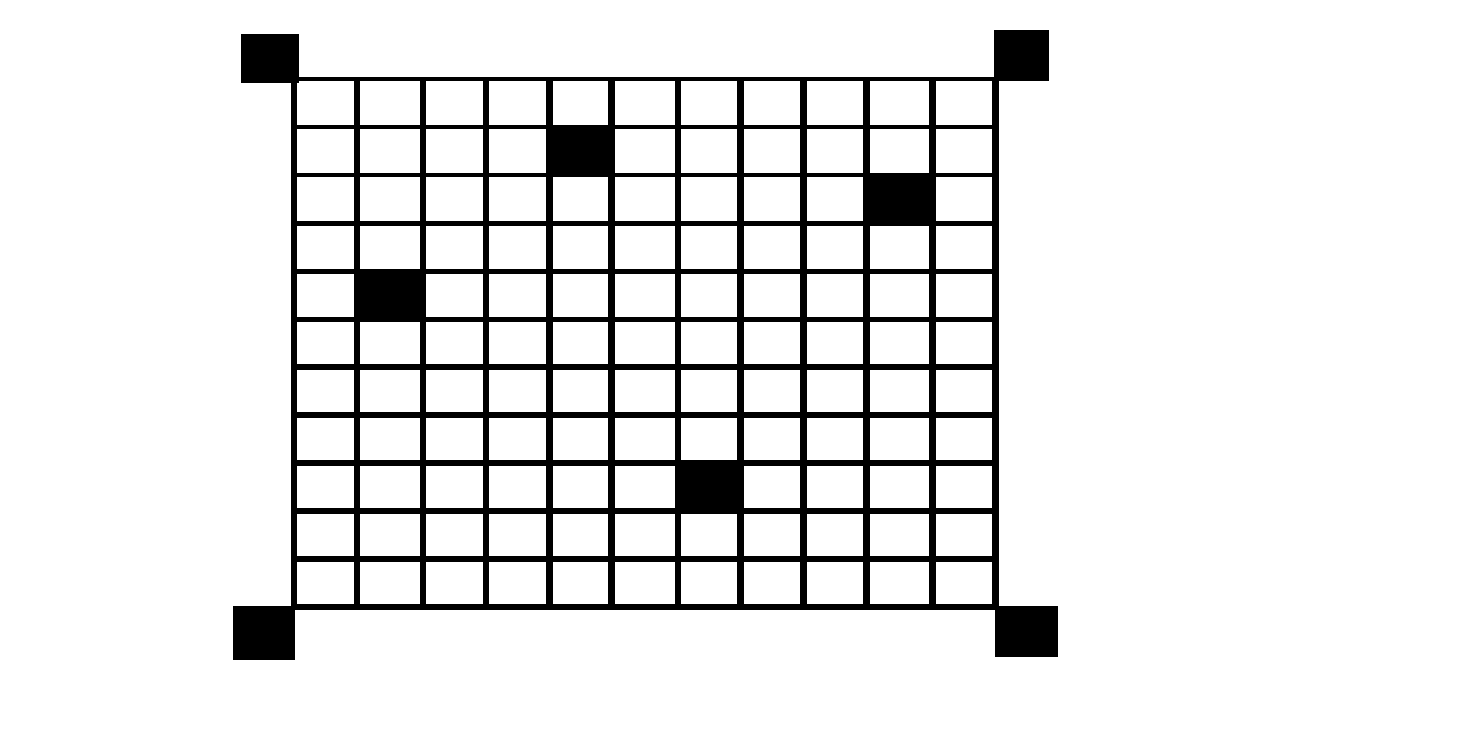
然后我们开始从左往右搜索，从右往左搜索和特殊情况搜索三个部分。
1.从左往右搜索
在算法开始前，我们先将障碍点(包括我们得到的4个)按横坐标排序（左右顺序）后得到如下编号：

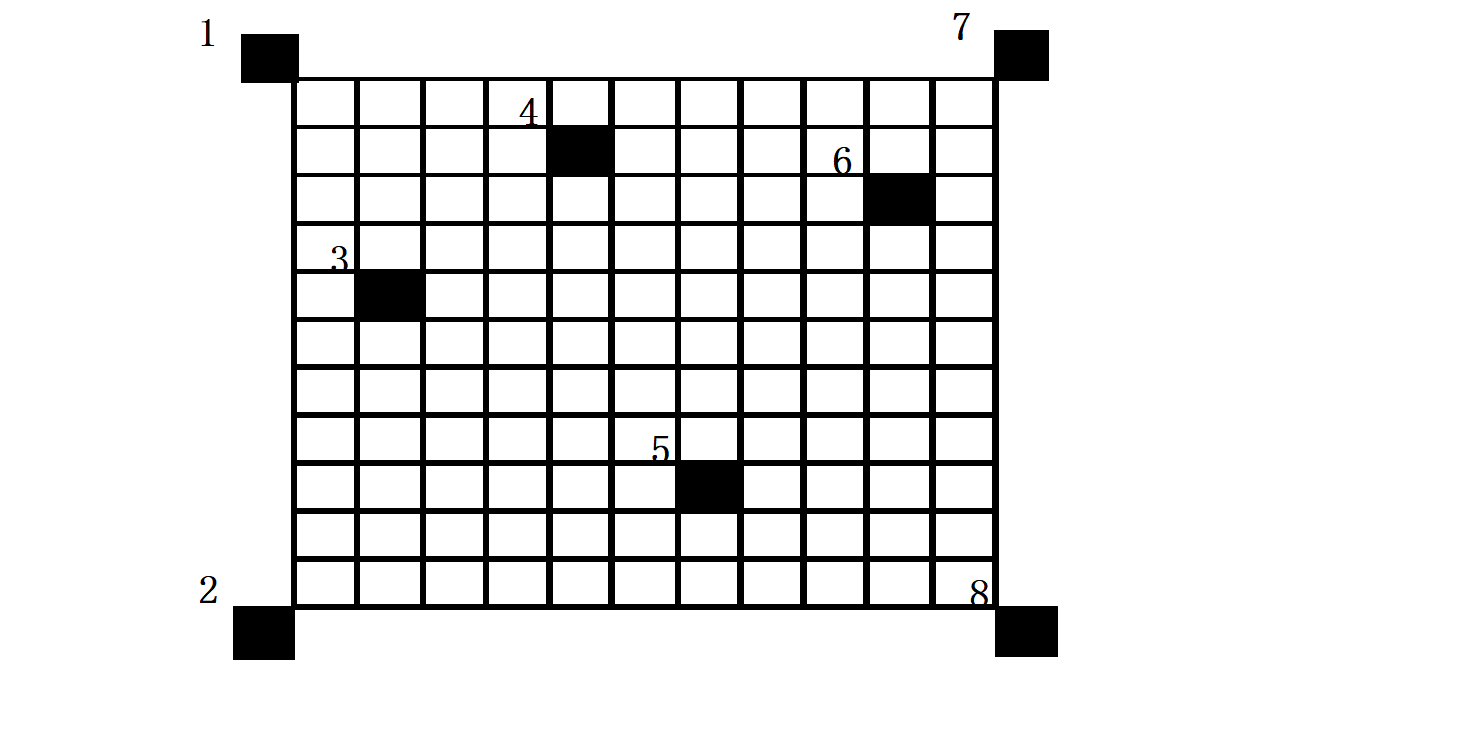
我们首先从1开始左往右枚举一个左边界，我们一个从1号障碍点开始，设左边界l此时为1号障碍点的右平面。一开始的极大子矩形上下边up,low为整个牛场的上下边界。

我们继续从左边界开始从左往右枚举一个右边界，开始时枚举到2号障碍点，设右边界r为此时2号障碍点的左平面，故如图：

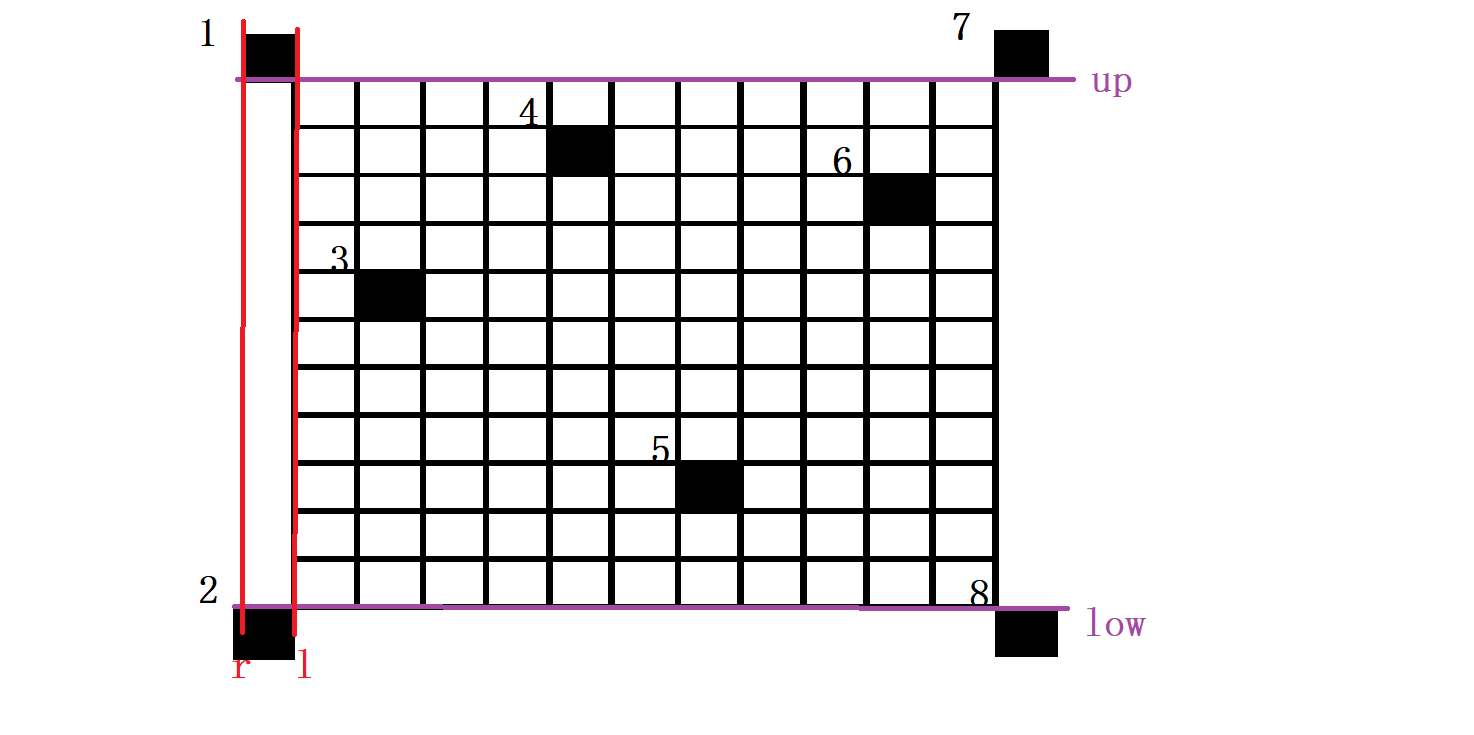
我们发现右边界r≤左边界l故此时极大子矩形面积为0。接下来需要对上下边界做一些修改，否则之后的极大子矩形可能会包括障碍点。因为2的纵坐标小于1的纵坐标，所以修改下边界，修改为2的上平面(其实没有变化)。

接着我们右边界r枚举到3号障碍点的左平面，故如图：

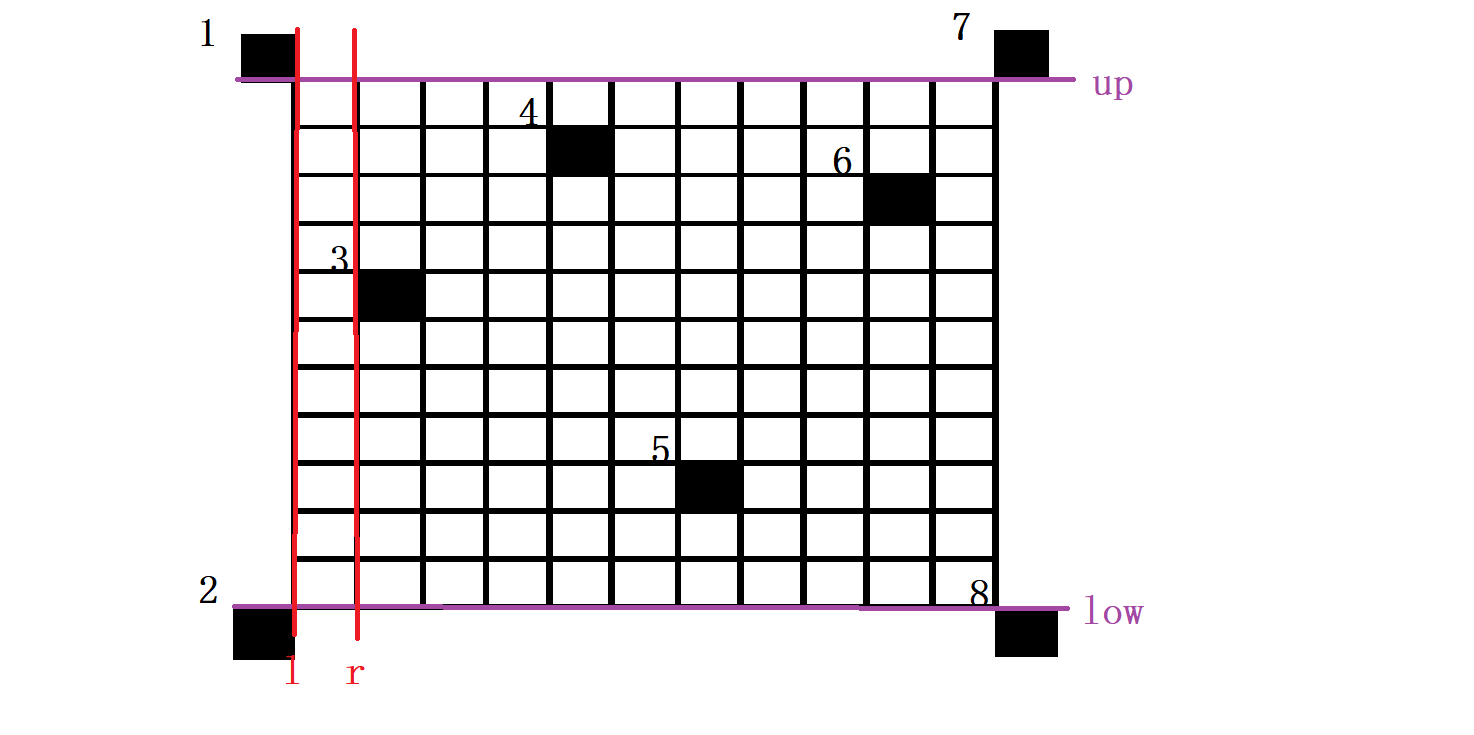
此时我们发现右边界r＞左边界l故此时极大子矩形面积有效为(up - low) * (r - l),即为两条红线和两条紫线一同框定的矩形。接下来需要对上下边界做一些修改。因为3的纵坐标小于1的纵坐标，所以修改下边界，修改为3的上平面。

接着我们右边界r枚举到4号障碍点的左平面，故如图：

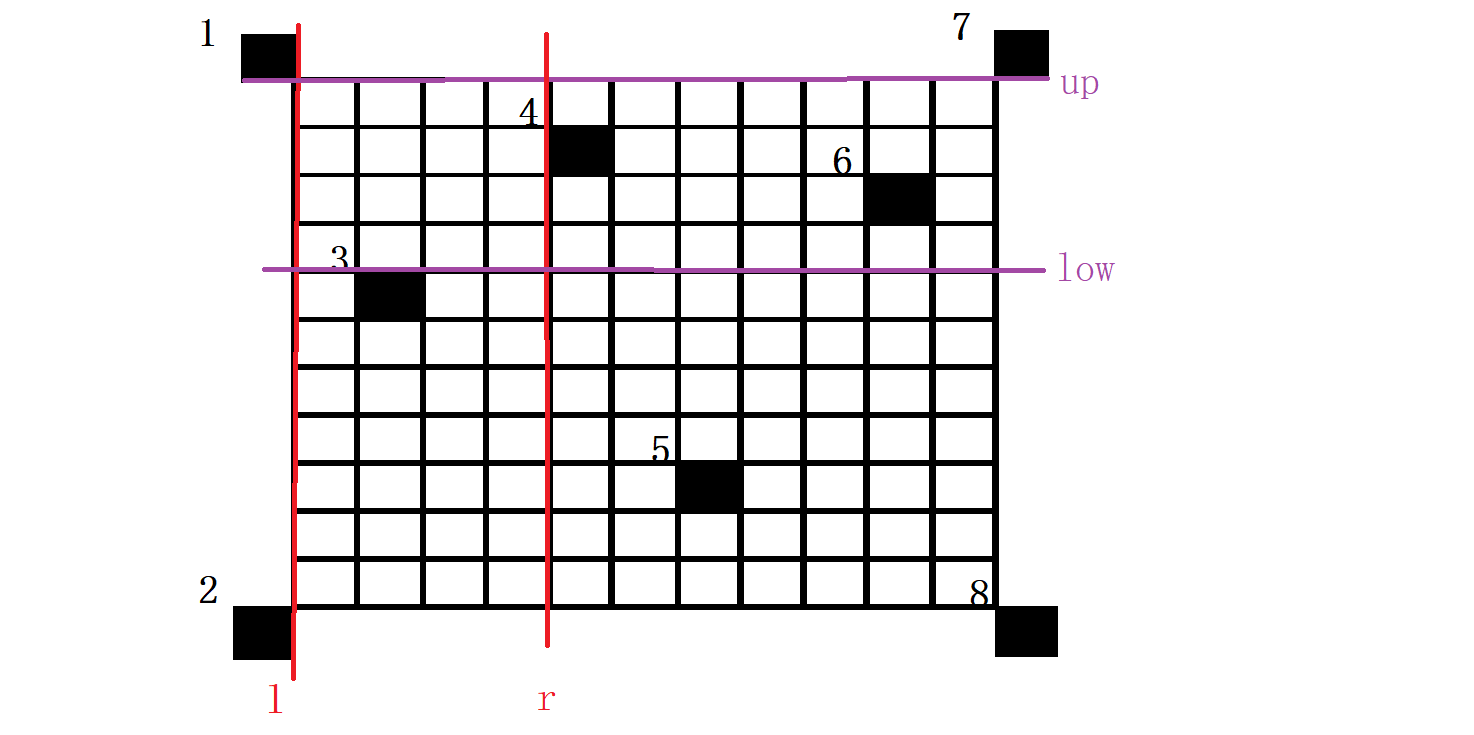
此时我们发现右边界r＞左边界l故此时极大子矩形面积有效为(up - low) * (r - l),即为两条红线和两条紫线一同框定的矩形…………

重复以上操作我们就能求出以1的右平面作为左边界的所有极大子矩形。但是1号障碍点毕竟是我们后加入的障碍点，太过于特殊，无法说明全部情况，为了方便说明，我们以3的右平面作为左边界继续进行一步一步讲解：

我们从左边界3开始从左往右枚举一个右边界，开始时枚举到4号障碍点，设右边界r为此时4号障碍点的左平面，故如图：

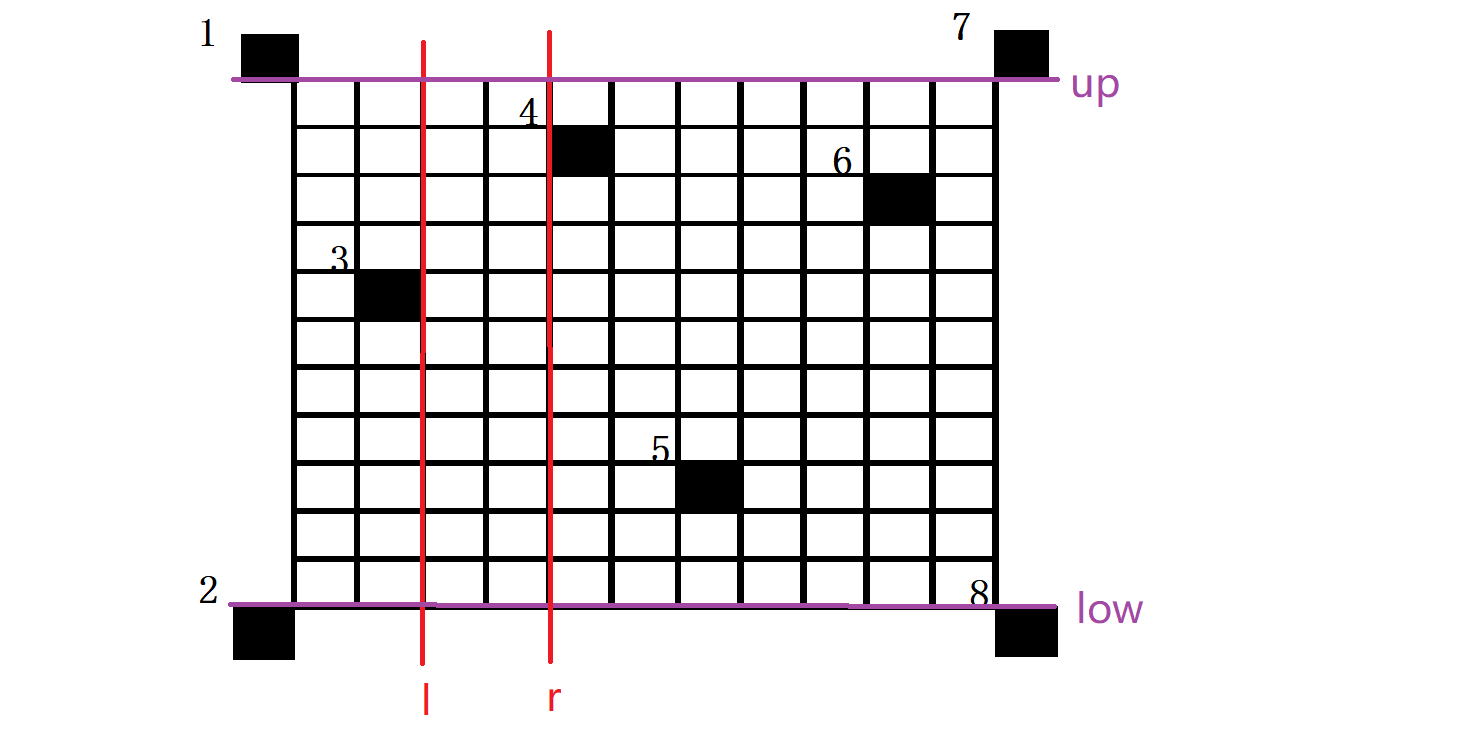
此时我们发现右边界r＞左边界l故此时极大子矩形面积有效为(up - low) * (r - l),即为两条红线和两条紫线一同框定的矩形。接下来需要对上下边界做一些修改。因为4的纵坐标大于3的纵坐标，所以修改上边界，修改为4的下平面。

接着我们右边界r枚举到5号障碍点的左平面，故如图：

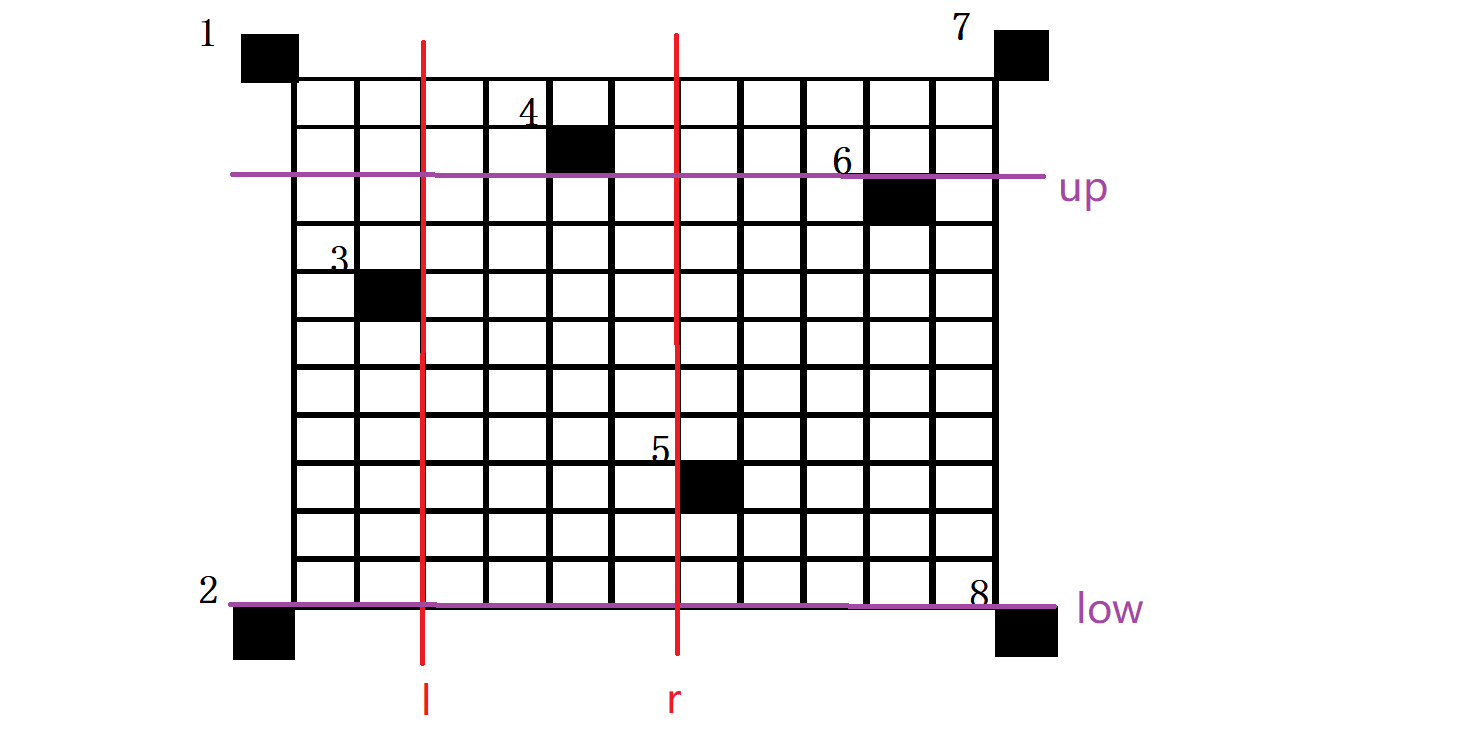
此时我们发现右边界r＞左边界l故此时极大子矩形面积有效为(up - low) * (r - l),即为两条红线和两条紫线一同框定的矩形。接下来需要对上下边界做一些修改。因5的纵坐标小于3的纵坐标，所以修改下边界，修改为5的上平面。

接着我们右边界r枚举到6号障碍点的左平面，故如图：

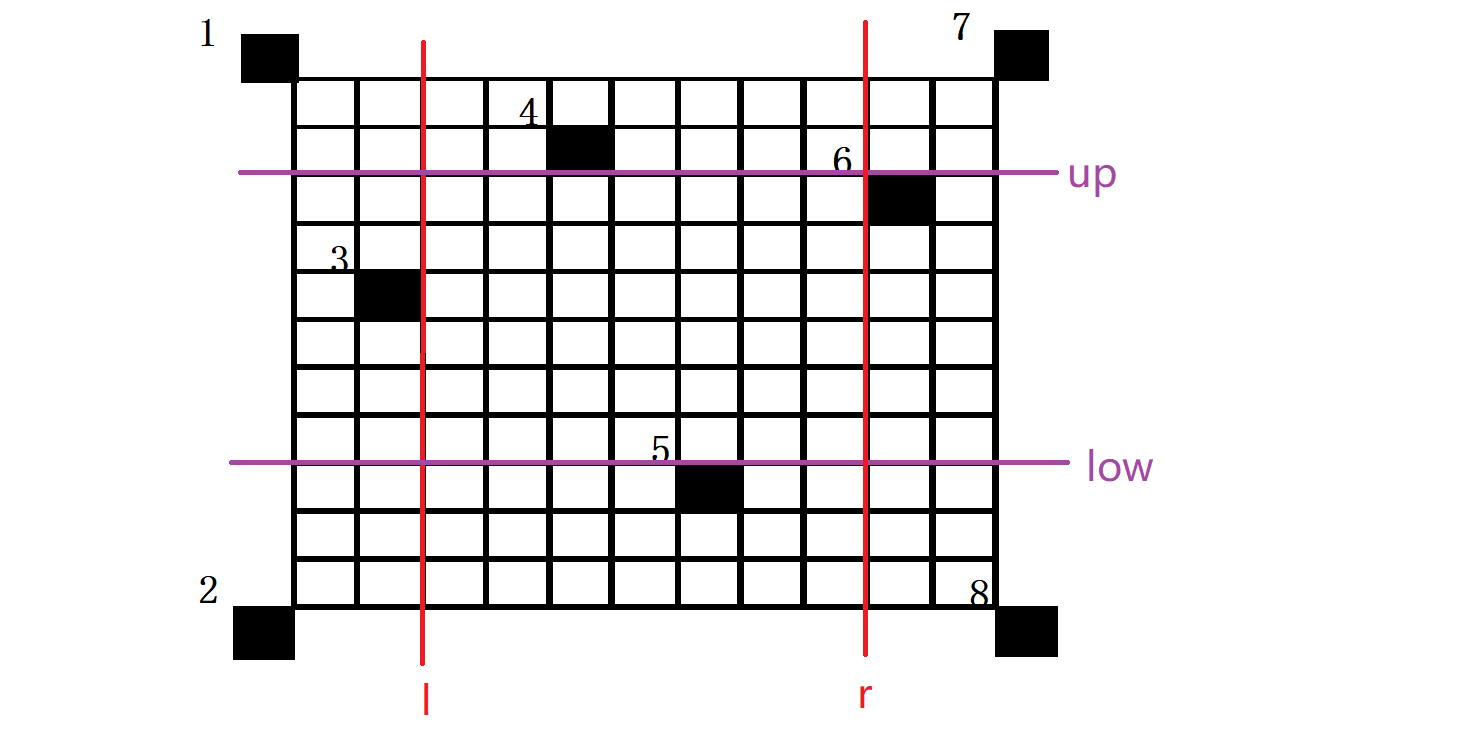
此时我们发现右边界r＞左边界l故此时极大子矩形面积有效为(up - low) * (r - l),即为两条红线和两条紫线一同框定的矩形。接下来需要对上下边界做一些修改。因6的纵坐标大于3的纵坐标，所以修改上边界，修改为6的下平面。

最后对于7和8其实都是一样的如图：

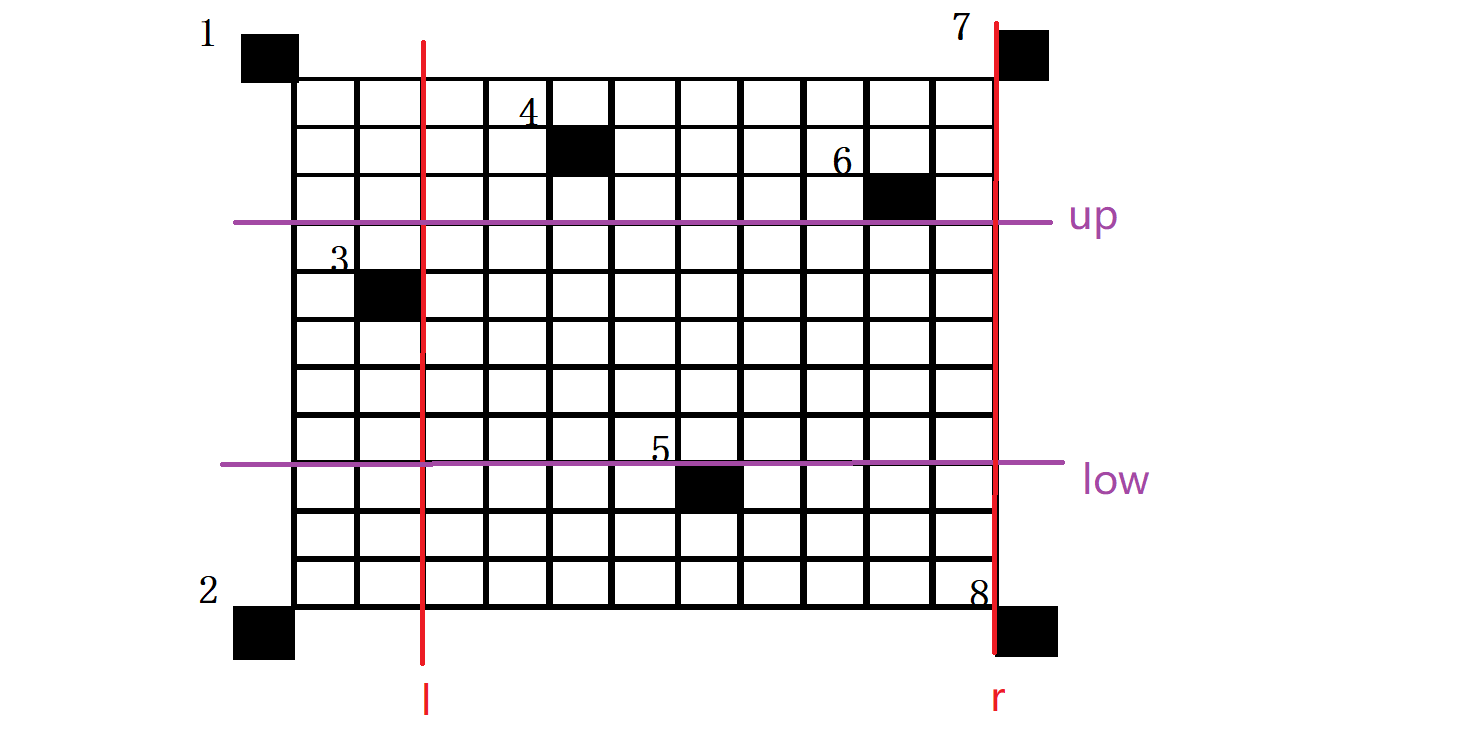
此时我们发现右边界r＞左边界l故此时极大子矩形面积有效为(up - low) * (r - l),即为两条红线和两条紫线一同框定的矩形。每次结束后都要记得修改上下边界！

那到这里是不是我们的所有情况都枚举完了呢？

2.从右往左搜索
从左往右搜后我们会发现有一些遗漏的情况，就是极大子矩形的左边界是矩形的左边界，右边界刚好是一个黑点的左平面情况，下图中的橙色矩形在我们之前从左往右的搜索中就没有被搜索到：

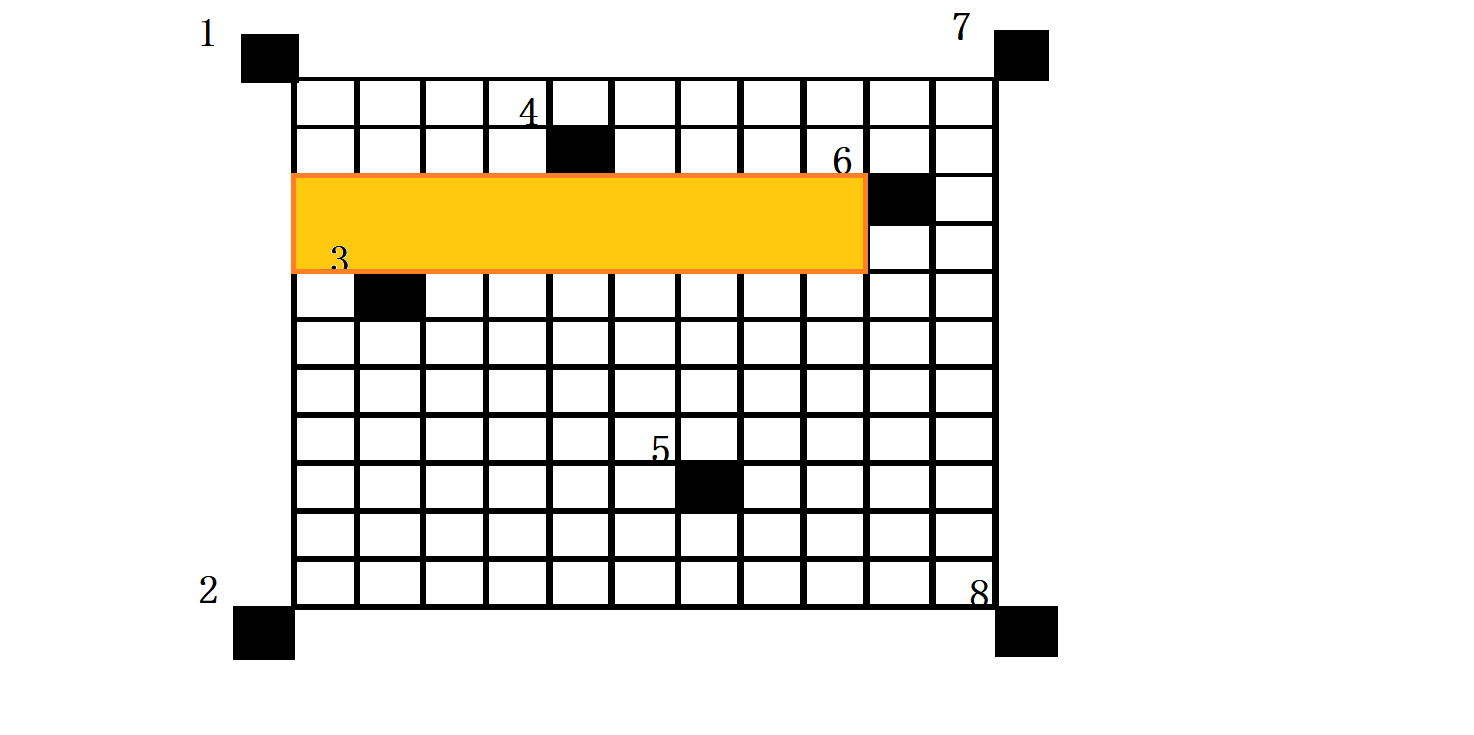
解决方法也很简单，我们只要按照刚刚的方法，调整一下搜索顺序，先搜索右边界，再搜索左边界就好啦。

3.特殊情况搜索

在从左往右搜和从右往左搜后我们发现还有一种情况没有考虑到，就是极大子矩形的左右边界都是矩形边界，如图蓝色矩形正是如此：

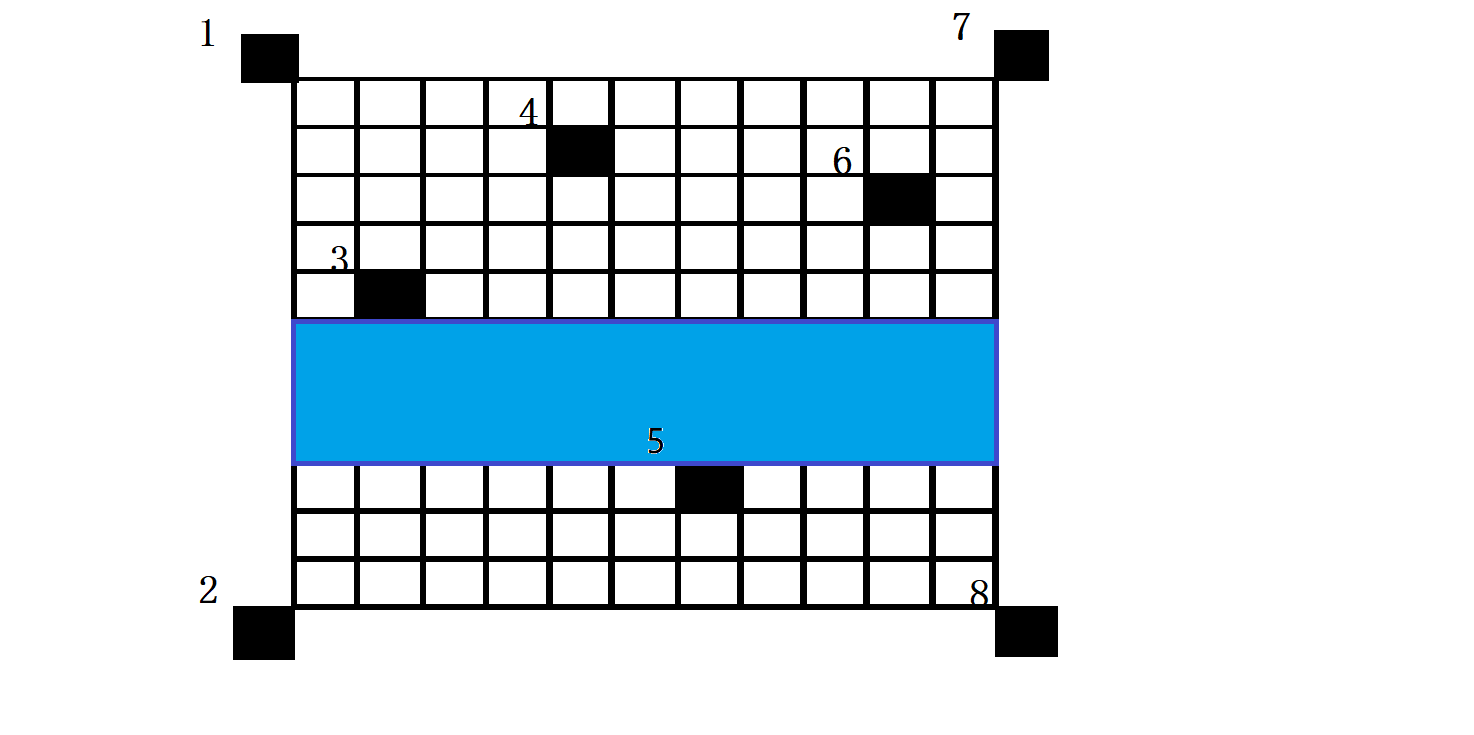
解决方法是，再将黑点按纵坐标重新排序，如图：

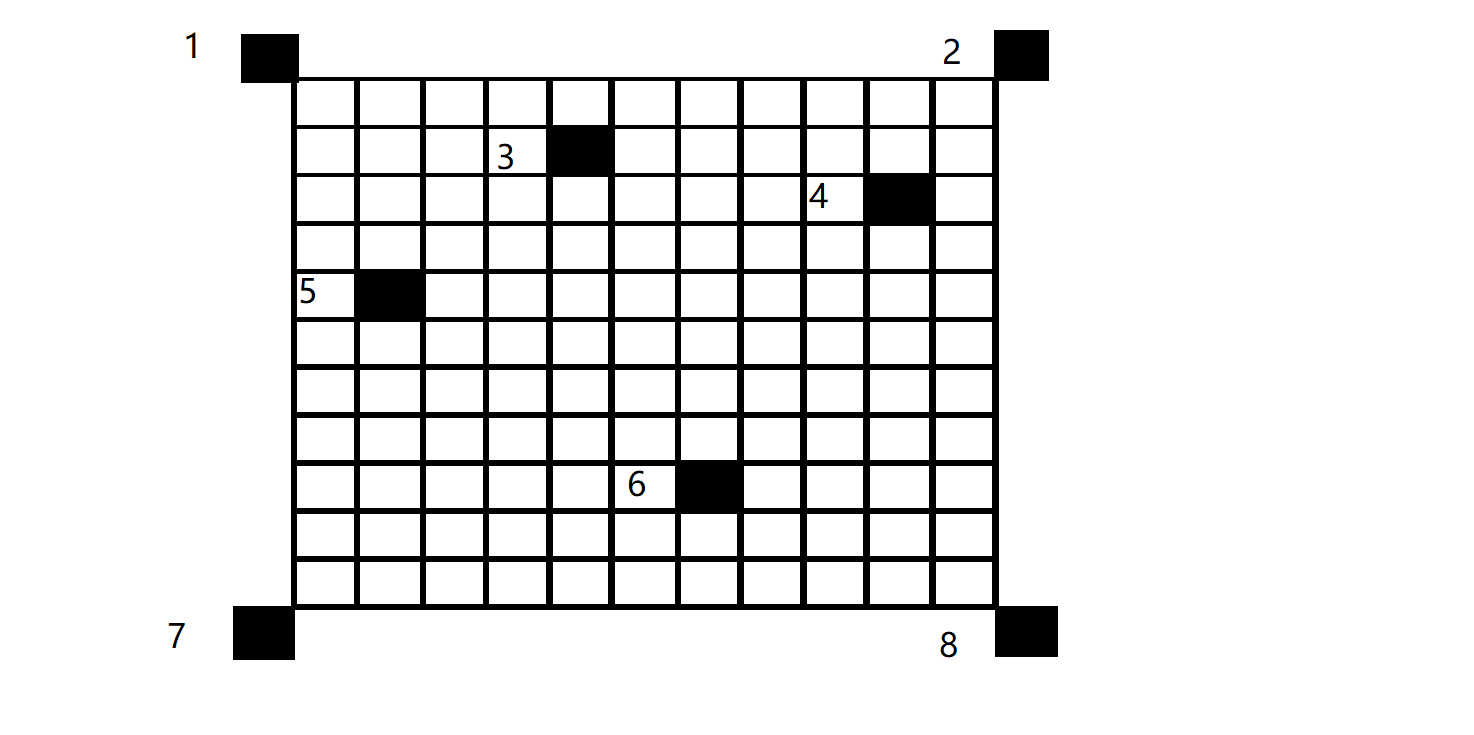
可以得到这类极大子矩形的面积就是编号相邻两个黑点（按纵坐标排序后）上下边界的距离乘以矩形的长。

前两部分的时间复杂度O(N^2)，第三部分是O(N)，排序的复杂度是O(NlogN),所以总的复杂度就是O(N^2)。其中N为障碍点数。

算法实现

下面附上对于上述问题的障碍点法代码模板：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
struct node {
    int x, y;
}a[1100000];
int graph[2200][2200];
int n, m, tot = 0, ans = 0;

bool compa(node a, node b) {
    if(a.x < b.x) return(true);
    else return(false);
}

bool compb(node a, node b) {
    if(a.y < b.y) return(true);
    else return(false);
}

int main() {
    scanf("%d%d", &n, &m); //读入图的大小
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            scanf("%d", graph[i][j]);
            if(graph[i][j] == 1) {
                tot++;
                a[tot].x = j;
                a[tot].y = i; 
                //水平为x轴，竖直为y轴，左上角为原点 
            }
        }
    } //读入图  
    a[++tot].x = 0; a[tot].y = 0;
    a[++tot].x = 0; a[tot].y = n + 1;
    a[++tot].x = m + 1; a[tot].y = 0;
    a[++tot].x = m + 1; a[tot].y = n + 1;

    //从左往右搜
    sort(a + 1, a + tot + 1, compa);
    for(int i = 1; i <= tot; i++) {
        int l = a[i].x , low = 0 , up = n + 1;
        for(int j = i + 1; j <= tot; j++) {
                int r = a[j].x;
                if(up <= low + 1) break;
                if(r >= l + 1) ans = max(ans , (r - l - 1) * (up - low - 1));
                if(a[j].y < a[i].y) low = max(low , a[j].y);//更新上下边界
                else up = min(up , a[j].y); 
        }
    }
    //从右往左搜  

    for(int i = tot; i >= 1; i--) {
        int r = a[i].x , low = 0 , up = n + 1;
        for(int j = i - 1; j >= 1; j--) {
                int l = a[j].x;
                if(up <= low + 1) break;
                if(r >= l + 1) ans = max(ans , (r - l - 1) * (up - low - 1));
                if(a[j].y < a[i].y) low = max(low , a[j].y);//更新上下边界
                else up = min(up , a[j].y); 
        }
    }

    //处理特殊情况
    sort(a + 1 , a + tot + 1 , compb); 
    for(int i = 1; i <= tot - 1; i++) {
        ans = max(ans , m * (a[i + 1].y - a[i].y - 1));
    }

    printf("%d", ans); 
    return 0;
}

对应可解决题目：[Luogu P4147]玉蟾宫的部分数据点。

当然这种算法应付的是矩阵很大但是障碍点（黑点）不多的情况，所以一般来说都是读入障碍点的个数和位置，但由于我没有找到原题就还剩用玉蟾宫来代替了。对于读入障碍点的个数和位置的问题我们只需要改变读入部分就好啦。

计算几何最大子矩形问题

问题描述

在计算几何最大子矩形问题相关问题中，一样有非常经典的题目计算最大空白子矩形。下面就让我们来看看问题描述。

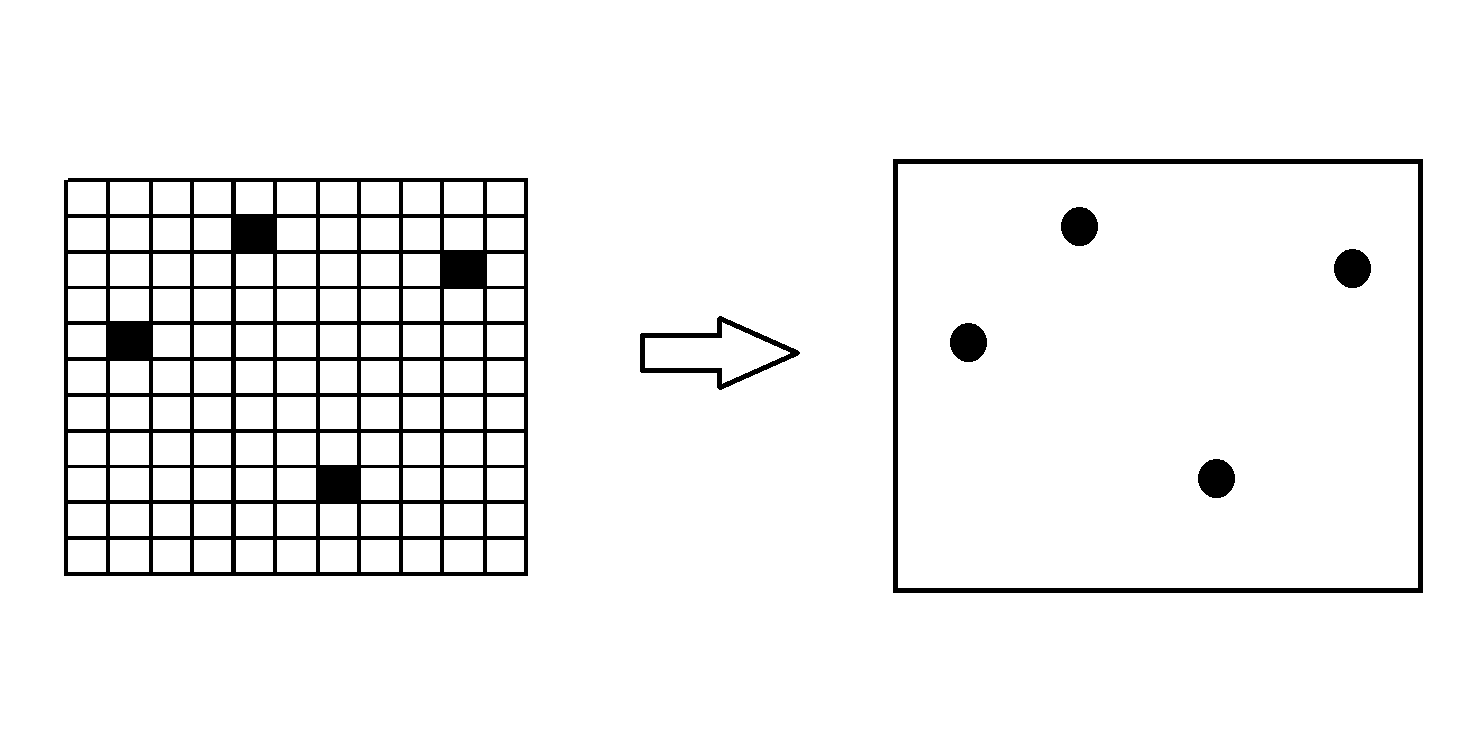
题目大意：在一个给定的大小为a*b矩形中有n个障碍点(坐标可以是实数)，要找出网格内部不包含任何障碍点，且边界与坐标轴平行的最大子矩形（障碍点可以在边界上）。

这题看起来和我们的矩形最大子矩形问题非常相似，只不过我们的问题从矩形网格变到了普通的矩形平面上，为了方便讲解这里的例子和代码的障碍点坐标和网格大小均为整数，其实实数也是一样改一下类型就好了：

我们的可选解决算法还是有悬线法和障碍点法两种方法。

悬线法

算法原理

悬线法由于其动态规划般的递推求悬线长度及其向左向右的最大拓展过程，本就是为矩形网格图而准备的，那这是不是代表着悬线法在这完全没有用武之地呢？当然不是的，今天我就来弘扬传统悬线文化，将悬线法如何运用在这个计算几何题目上告诉你。

说到将平面上的实数点变成网格，你的第一反应是什么，没错就是离散化，我们将左边离散化后，并将障碍点的长宽都设置成0，排序后相邻的障碍点之间的白格子长款为障碍点之间的坐标差就好啦，比如加入我们在10*10的矩形网格里有两个障碍点（3，9）和（8，2），我们可以离散化成下面这样：

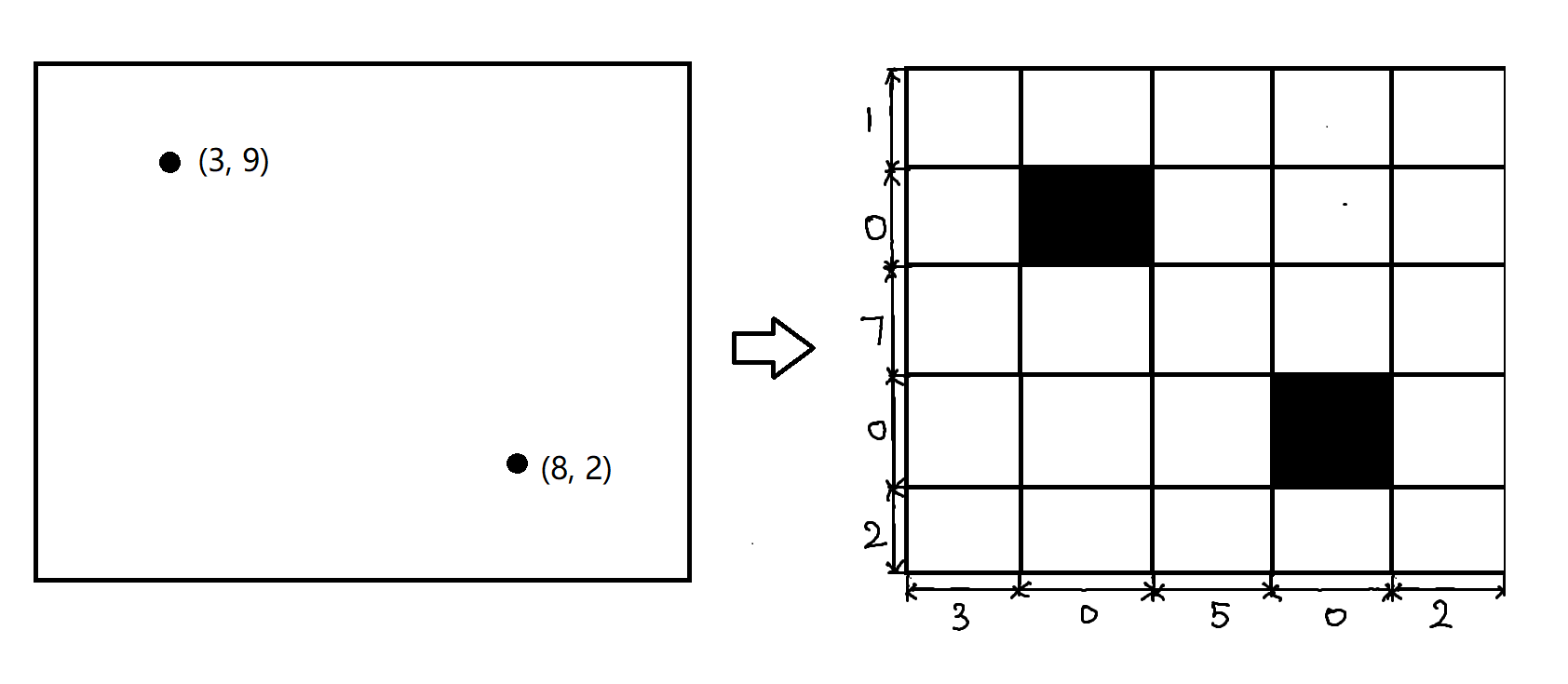
我们的题目就变成了每个格子都有自己的长宽的悬线法了，其实过程也还是一样的，我们先对于每个格点，找到他们的上悬线长度h：

然后再找到每条悬线向左向右的最大拓展距离l和
r（包括这个格子的宽k）：

然后用（l + r - k）*h去更新答案就好啦。

算法实现

下面附上对于上述问题的悬线法代码模板：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
struct node {
    int x, y;//原始坐标 
    int xx, yy;//离散化后在矩形中的坐标 
}a[1100000];
int graph[2200][2200];
int l[2200][2200] = {0}, r[2200][2200] = {0}, h[2200][2200] = {0};
int L[2200][2200] = {0}, R[2200][2200] = {0};
int x_length[2200], y_length[2200];
int n = 0, m = 0, ans = 0, tot, width, length;
//n为矩形行数，m为矩形列数 
bool compa(node a, node b) {
    if(a.x < b.x) return(true);
    else return(false);
}

bool compb(node a, node b) {
    if(a.y < b.y) return(true);
    else return(false);
}
int main() {
    scanf("%d%d", &length, &width); //读入图的大小
    scanf("%d", &tot);
    for(int i = 1; i <= tot; i++) scanf("%d%d", &a[i].x, &a[i].y); 
    a[0].x = 0; a[0].y = 0;

    sort(a + 1, a + tot + 1, compa);
    for(int i = 1; i <= tot; i++) {
        if(a[i].x != a[i - 1].x) {
            m++;
            x_length[m] = a[i].x - a[i - 1].x;

            m++;
            a[i].xx = m;
            x_length[m] = 0;
        }
        else {
            if(m > 0) a[i].xx = m;
            else {
                m++;
                a[i].xx = m;
                x_length[m] = 0;
            }
        }
    } 
    if(length > a[tot].x) {
        m++;
        x_length[m] = length - a[tot].x;
    }
    //离散化横坐标

    sort(a + 1, a + tot + 1, compb);
    for(int i = 1; i <= tot; i++) {
        if(a[i].y != a[i - 1].y) {
            n++;
            y_length[n] = a[i].y - a[i - 1].y;

            n++;
            a[i].yy = n;
            y_length[n] = 0;
        }
        else {
            if(n > 0) a[i].yy = n;
            else {
                n++;
                a[i].yy = n;
                y_length[n] = 0;
            }
        }
    } 
    if(width > a[tot].y) {
        n++;
        y_length[n] = length - a[tot].y;
    }
    //离散化纵坐标

    for(int i = 1; i <= tot; i++) {
        graph[a[i].yy][a[i].xx] = 1;
    } 

    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            if(graph[i][j] == 1) h[i][j] = 0;
            else h[i][j] = h[i - 1][j] + y_length[i];
        }
    } //求向上悬线长度
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            if(graph[i][j] == 1) l[i][j] = 0;
            else l[i][j] = l[i][j - 1] + x_length[j];
        }
    } //求向左悬线长度
    for(int i = 1; i <= n; i++) {
        for(int j = m; j >= 1; j--) {
            if(graph[i][j] == 1) r[i][j] = 0;
            else r[i][j] = r[i][j + 1] + x_length[j];
        }
    } //求向右悬线长度

    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= m; j++) {
            if(h[i][j] > y_length[i]) {
                L[i][j] = min(L[i - 1][j], l[i][j]);
                R[i][j] = min(R[i - 1][j], r[i][j]);
            } //如果不是悬线开头 
            else {
                L[i][j] = l[i][j];
                R[i][j] = r[i][j];
            } //如果是悬线开头 

            ans = max(ans, h[i][j] * (L[i][j] + R[i][j] - x_length[j]));//更新答案 
        }
    }

    printf("%d", ans);
    return 0;
}

对应可解决题目：[Luogu P1578]奶牛浴场的部分数据点，有些点过不去的原因是这样写空间复杂度是4*n^2，在极限数据时空间会不足够。

障碍点法

算法原理

其实障碍点法的设计初衷就是为计算几何的这个问题而准备的，只是被我魔改到了可以应用到矩形最大子矩形问题上（好像没有别的博客这么干？）。大体思路还是不变的，变的只是我们的障碍点从有面积的格点变成了没有实体面积的质点。我们还是来回顾一下。

我们的算法从左往右搜索，从右往左搜索和特殊情况搜索三个部分。
1.从左往右搜索
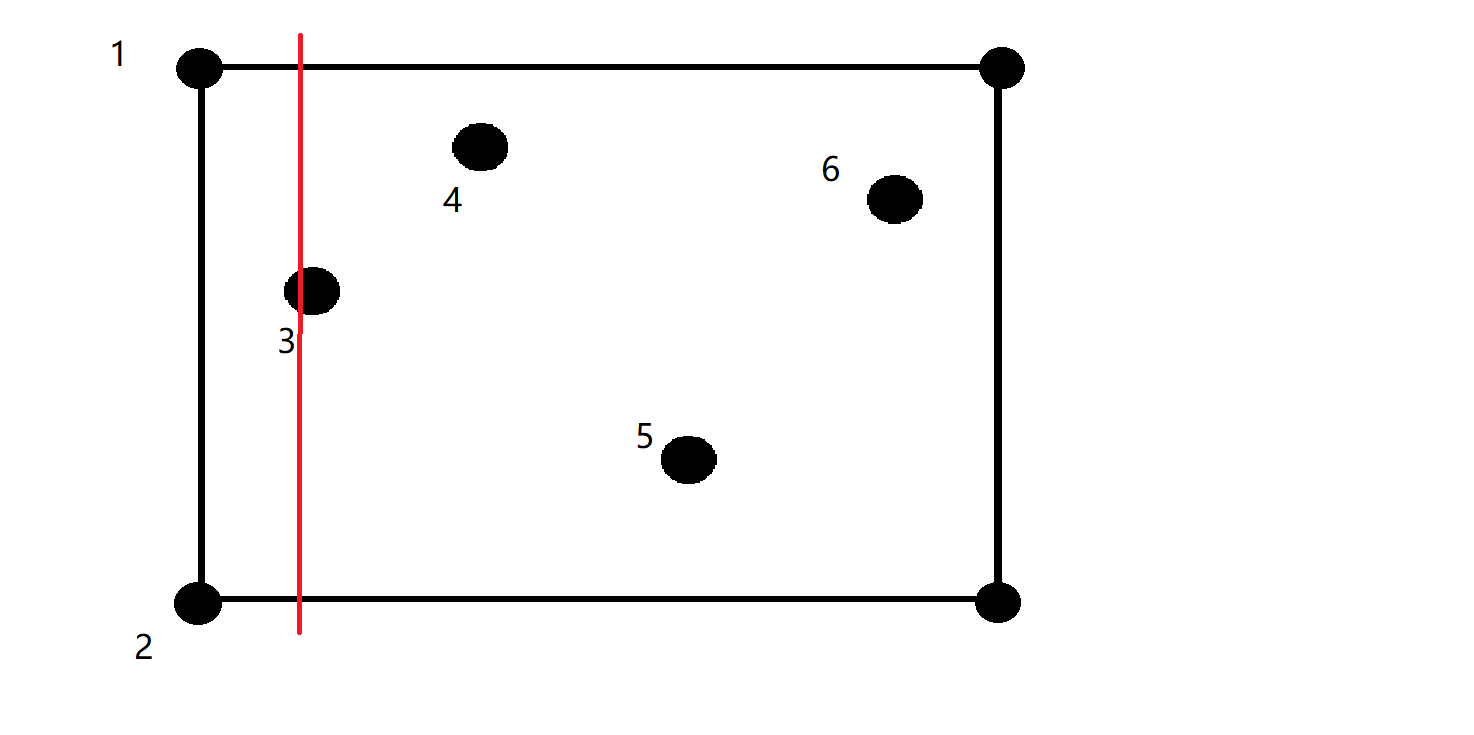
在算法开始前，我们先将障碍点(包括我们得到的4个)按横坐标排序（左右顺序）后得到如下编号：

然后接下来的步骤都是一样的，为了方便演示我们还是选用3号点作为我们的左边界，开始时上下边界还是我们的矩形区域的上下边界：

开始时有边界枚举到4号障碍点，设右边界r为此时4号障碍点，故如图：

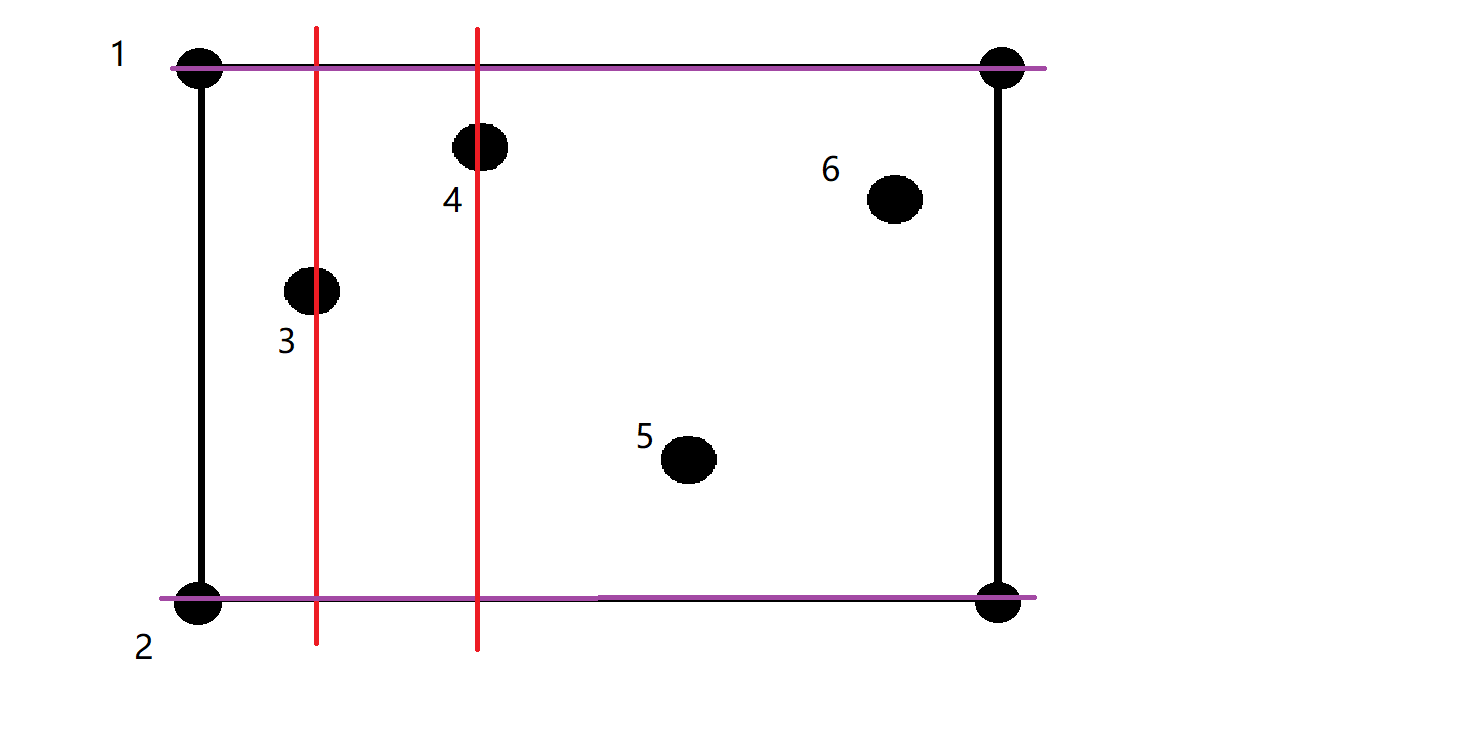
此时极大子矩形面积有效为(up - low) * (r - l),即为两条红线和两条紫线一同框定的矩形。接下来需要对上下边界做一些修改。因为4的纵坐标大于3的纵坐标，所以修改上边界，修改为4的纵坐标。

接着我们右边界r枚举到5号障碍点，故如图：

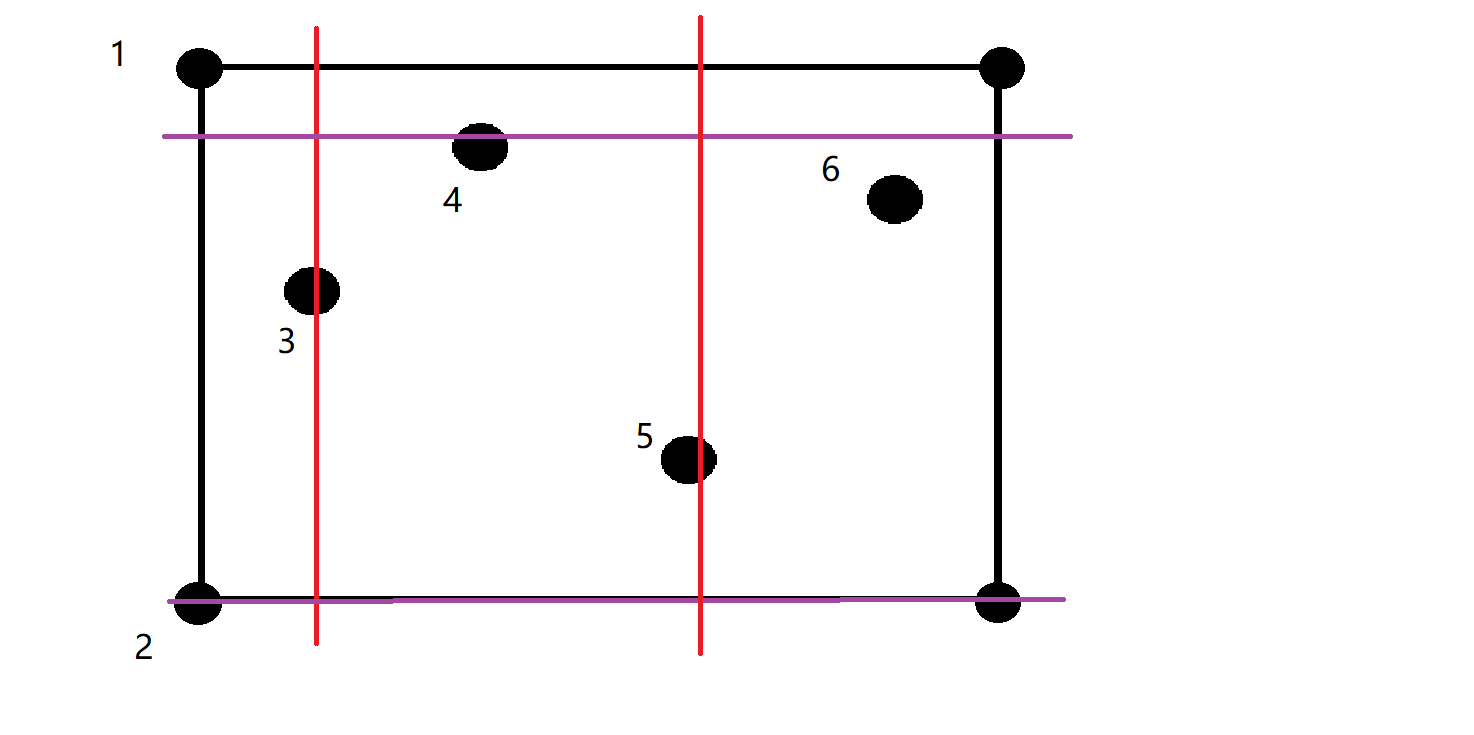
此时极大子矩形面积有效为(up - low) * (r - l),即为两条红线和两条紫线一同框定的矩形。接下来需要对上下边界做一些修改。因5的纵坐标小于3的纵坐标，所以修改下边界，修改为5的纵坐标。

接着我们右边界r枚举到6号障碍点，故如图：

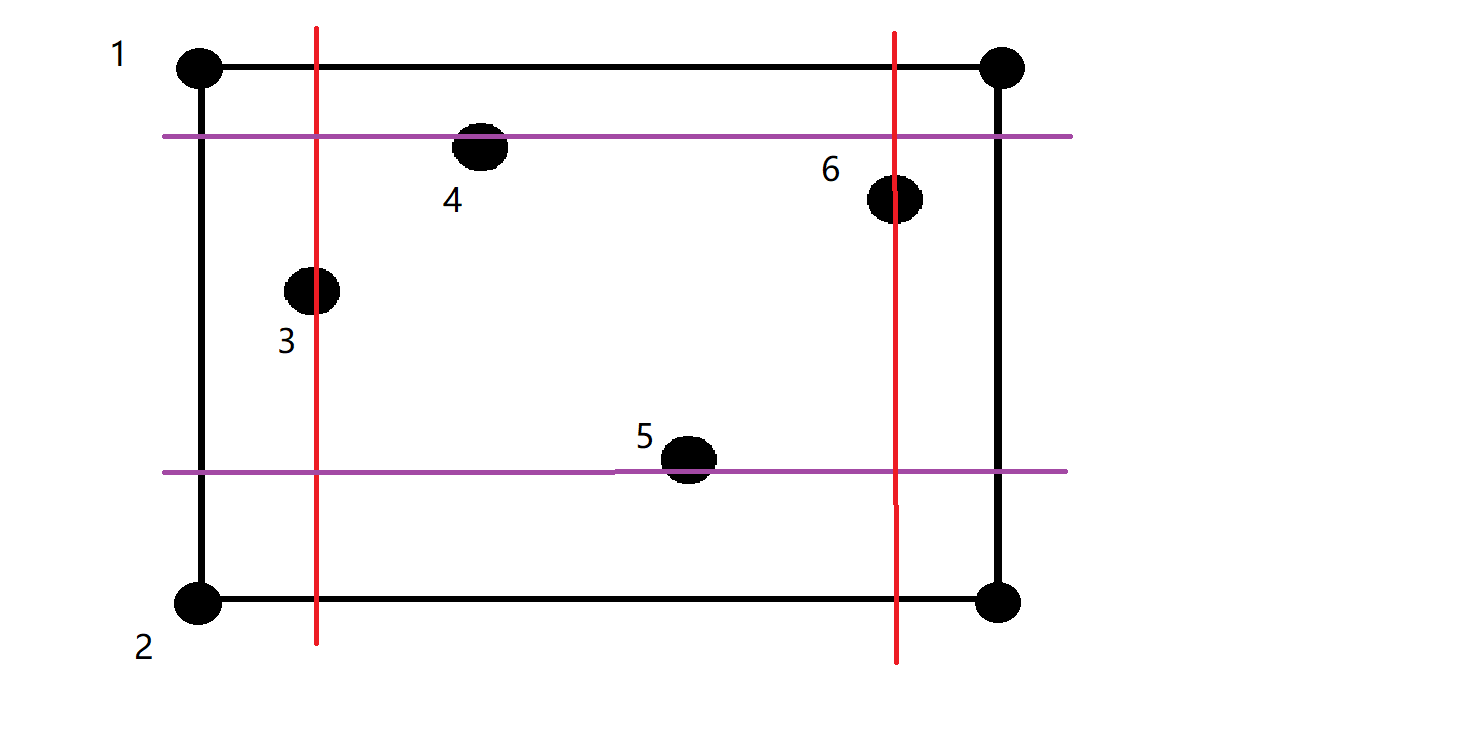
此时极大子矩形面积有效为(up - low) * (r - l),即为两条红线和两条紫线一同框定的矩形。接下来需要对上下边界做一些修改。因6的纵坐标大于3的纵坐标，所以修改上边界，修改为6的纵坐标。

最后对于7和8其实都是一样的如图：

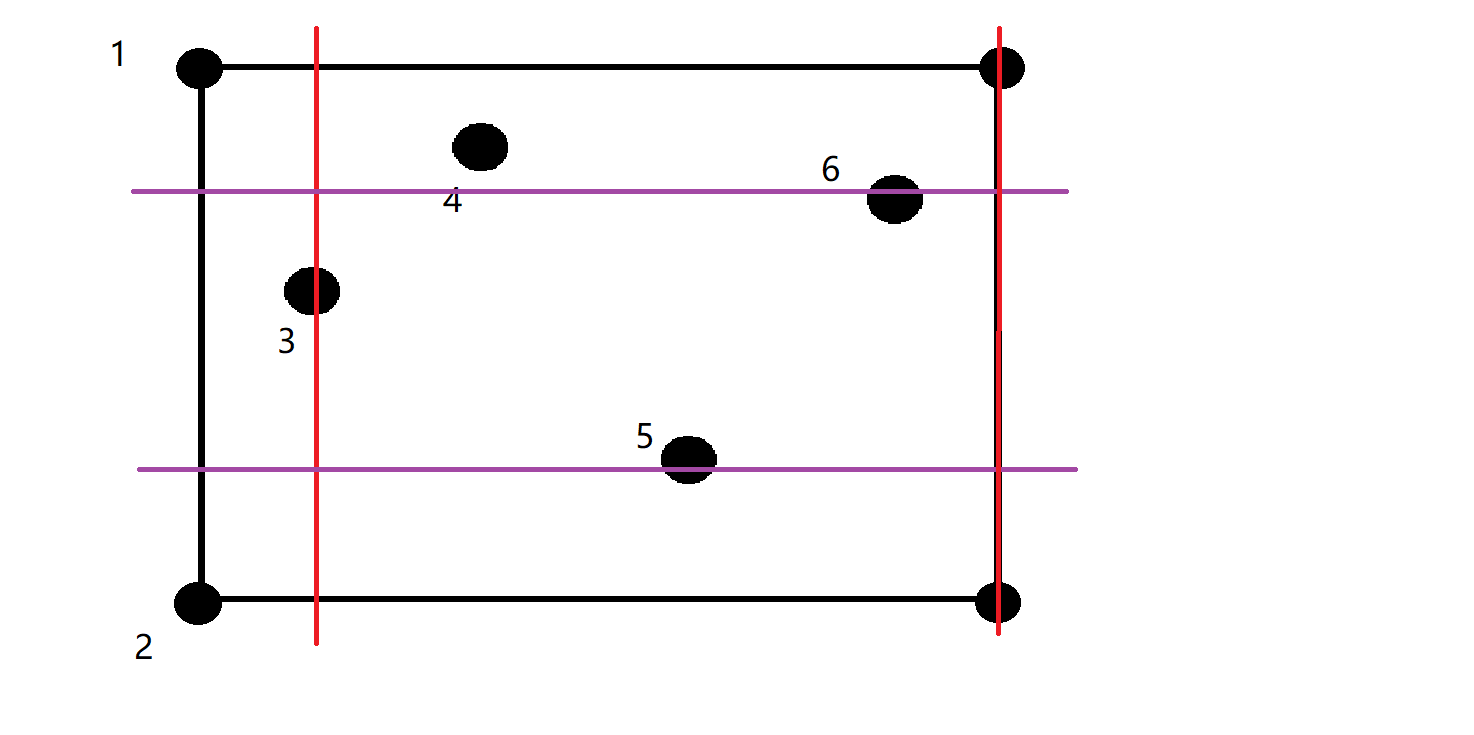
此时我们发现右边界r＞左边界l故此时极大子矩形面积有效为(up - low) * (r - l),即为两条红线和两条紫线一同框定的矩形。

到这里从左向右搜索就完成了，是不是和矩形那里的完全一样呢？只是少了每个格点的上下左右平面概念，变成了实打实的坐标而已。

2.从右往左搜索
同样地从左往右搜后我们会发现有一些遗漏的情况，就是极大子矩形的左边界是矩形的左边界，右边界刚好是一个黑点的左平面情况，我们要做的也一样是按照刚刚的方法，调整一下搜索顺序，先搜索右边界，再搜索左边界就好啦。

3.特殊情况搜索

同样地，在从左往右搜和从右往左搜后我们发现还有一种情况没有考虑到，就是极大子矩形的左右边界都是矩形边界，解决方法也同样是是，再将黑点按纵坐标重新排序，可以得到这类极大子矩形的面积就是编号相邻两个黑点（按纵坐标排序后）上下边界的距离乘以矩形的长。这里就不过多赘述了。

代码实现

下面附上对于上述问题的障碍点法代码模板：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
struct node {
    int x, y;
}a[1100000];
int n, m, tot = 0, ans = 0;

bool compa(node a, node b) {
    if(a.x < b.x) return(true);
    else return(false);
}

bool compb(node a, node b) {
    if(a.y < b.y) return(true);
    else return(false);
}

int main() {
    scanf("%d%d", &n, &m); //读入图的大小，长为n宽为m 
    scanf("%d", &tot); //读入障碍点个数 
    for(int i = 1; i <= tot; i++) scanf("%d%d", &a[i].x, &a[i].y); 
    a[++tot].x = 0; a[tot].y = 0;
    a[++tot].x = 0; a[tot].y = m;
    a[++tot].x =n; a[tot].y = 0;
    a[++tot].x = n; a[tot].y = m;

    //从左往右搜
    sort(a + 1, a + tot + 1, compa);
    for(int i = 1; i <= tot; i++) {
        int l = a[i].x , low = 0 , up = m;
        for(int j = i + 1; j <= tot; j++) {
                int r = a[j].x;
                if(up <= low) break;
                if(r >= l) ans = max(ans , (r - l) * (up - low));
                if(a[j].y < a[i].y) low = max(low , a[j].y);//更新上下边界
                else up = min(up , a[j].y); 
        }
    }
    //从右往左搜  

    for(int i = tot; i >= 1; i--) {
        int r = a[i].x , low = 0 , up = m;
        for(int j = i - 1; j >= 1; j--) {
                int l = a[j].x;
                if(up <= low) break;
                if(r >= l) ans = max(ans , (r - l) * (up - low));
                if(a[j].y < a[i].y) low = max(low , a[j].y);//更新上下边界
                else up = min(up , a[j].y); 
        }
    }

    //处理特殊情况
    sort(a + 1 , a + tot + 1 , compb); 
    for(int i = 1; i <= tot - 1; i++) {
        ans = max(ans , n * (a[i + 1].y - a[i].y));
    }

    printf("%d", ans); 
    return 0;
}

对应可解决题目：[Luogu P1578]奶牛浴场。

结语

通过这篇博客，相信你也已经对最大子矩形问题有了自己的理解，在很多情况下悬线法和障碍点法都是可做的，具体选择哪一种算法还是要根据题目的数据范围灵活选择。最后希望你喜欢这篇BLOG！