说到动态规划,就不得不提到区间动态规划这一重要分支。到现在都还记得当年还是OIER的时候第一次了解到区间动态规划时被其精妙的设计所折服的喜悦。所以现在就让我们一同学习以下区间动态规划,回顾当年的那份喜悦吧!
区间动态规划
在之前的BLOG中,我们已经学习了动态规划的一些基本知识。那么什么是区间动态规划?和我们之前学过的线性动态规划有什么区别呢?
区间动态规划,从名字来看就是在一段区间上进行动态规划也就是说其对象是一段区间。正是如此,区间动态规划就是在动态规划的过程中求一个区间的最优解。一般来说我们通过将一个大的区间分为很多个小的区间,求其小区间的解,然后一个一个的组合成一个大的区间而得出最终解,这与分治有着异曲同工的巧妙之处。
接下来我们用之前学到的动态规划四步法来看看区间动态规划的常用套路。
第一步:确定状态——原问题是什么?子问题是什么?
原问题:一般来说是求区间[1, n]的最优值
子问题:求区间[i, j]的最优值
一般来说我们用用f[i][j]表示区间[i,j]的最优值
第二步:确定状态转移方程和边界
我们一般枚举分割点k,将[i, j]区间分为[i, k]和[k + 1, j]两部分,所以我们有f[i][j]=max/min(f[i][j],f[i][k]+f[k+1][j]+something)
初始化:f[i][i]=0/other (i=1->n)为什么这么做呢?很好理解,就是只包含自己本身的时候,也就是区间长度为1,值肯定是确定的,但具体是什么就要看题目而定了。
第三步:考虑是否需要优化
一般来说区间动态规划没什么特别的优化方法,一定要优化的话只能基于题目的性质减小搜索空间。
第四步:确定实现方法
一般来说对于区间动态规划,我们写记忆化搜索是比较方便的,大致框架如下:
int dfs(int l, int r) {
if(l == r) f[l][r] = ……;
if(f[l][r] > 0) return(f[l][r]);
for(int k = l; k < r; k++) {
int temp = dfs(l, k) + dfs(k + 1, r) + ……;
ans = max(temp, ans);
}
return ;
} 但有的同学可能要问了,我就喜欢写循环递推,可以吗?其实是完全没有问题的,大致框架如下:
for (int len = 2; len <= n; len++) {//len:长度 ,l:左区间断点,r:又区间端点
for (int l = 1; l + len - 1 <= n; l++) {//保证(l,r)的长度为len,且不越界
int r = l + len - 1;
for (int k = l; k <= r; k++) {//枚举间断点k
f[l][r] = max/min(f[l][r], f[l][k] + f[k+1][r] + something);
}
}
} 我们按照区间从小到大进行枚举就能保证我们在计算长度为len的区间f[l][r]时,长度小于len的区间f[l][k] 和 f[k+1][r]都已经被计算出来了,这样我们就能顺利计算出f[l][r]。
当然还有其他写法也是合法的,但都大同小异。以上这两种是我个人认为最好理解也是最好写的两种。下面就让我们看看具体例题,看看这些理论知识如何放到实践当中吧。
经典例题
括号匹配
题目大意:给出一个括号序列,求出其中最大匹配的括号数
例子:
((())) 6
()()() 6
([]]) 4
)[)( 0
([][][) 6
看到这题相信不少同学已经想起了这道题的简单版——给出一个只有(的括号序列,求出其中最大匹配的括号数。这个简单版我们的解法是开一个栈,遇到左括号就进栈,遇到右括号就让一个左括号出栈然后ans+=2(如果栈不空)。
那这道题能不能也用这种方法,我们开一个栈,遇到左括号就把它进栈,遇到右括号如果刚好和栈顶左括号匹配就让一个左括号出栈然后ans+=2,不匹配或者栈空就直接略过呢?显然是不行的,我们来看一个例子,对于括号序列([),如果按照刚刚讲的方法,答案是0;但是实际上([)的两个小括号可以匹配,答案是1,这就找到反例了。
那么又有聪明的同学肯定要问了。那我能不能开三个栈,分别维护大括号,中括号和小括号呢?好像上面讲的例子也能跑过啊。但实际上这也是错误的。现在我让你看看反例。对于{([)}],如果我们使用栈就会发现所有括号都是能匹配的,但其实不然,我们发现{([)}]最多只能匹配四个。因为形如([)]的序列很显然不是合法的括号匹配。
所以我们发现一个一个括号讨论是不好做的,那怎么办呢?没错我们的区间动态规划就要出马了。我们考虑f[i][j] 表示ai……aj的串中,有多少个已经匹配的括号。我们枚举一个k,分情况讨论:
- 如果ai与ak是匹配的,那么我们有
f[i][j] = max(f[i][j], f[i + 1][k - 1] + f[k + 1][j] + 2)(相当于是将i到j分成[xxxxx]xxxxx两部分)。 - 否则
f[i][j] = f[i + 1][j](将第一个元素去掉——因为它肯定不能算,它无法和区间内任意括号匹配)。最后记得边界f[i][i] = 0。
在实现方面的话递推和记忆化搜索都能写,但是还是推荐记忆化搜索会让思维量大大减小。
最长回文子序列长度
问题描述:给你一个长度为n 的序列,求最长回文子序列长度。(一般来说没有特殊说明,子串就是连续的,子序列就可以是不连续的)
同样地我们还是沿用刚刚的思路,我们设f[i][j] 表示ai……aj的串中,最长回文子序列长度。接下来我们分情况讨论:
- 如果ai与aj是一样的
f[i][j]= f[i+1][j-1]+2 - 否则: f[i][j] = max(f[i+1][j], f[i][j-1]) (既然匹配不上就抛弃前一个或者后一个)
在实现方面的话还是推荐记忆化搜索,自己去写一写就知道真的很方便快捷。
接下来我们考虑一下我们既然能用区间动态规划求出最长回文子序列长度能不能求出最长回文子串长度呢?也就是给你一个长度为n 的序列,求最长回文子串长度。
其实对于这个问题,我们有O(n)的算法Manacher,感兴趣的同学可以点击这里进行学习。那假如在考场上突然想不起Manacher怎么写,n又不是很大怎么办?没错我们也可以使用区间动态规划在O(n^2)的时间复杂度下完成。下面我们就来一起看看具体怎么做。
我们如果还是设f[i][j] 表示ai……aj的串中,最长回文子序列长度,你就发现出现了问题。我们不知道ai和aj这个首尾有没有取就很不好转移。所以我们这次设f[i][j] = 0/1表示ai……aj这个串是不是回文串。若为回文串则取1反之取0。
那么我们就很容易的知道:
- f[i][j] = 1(if f[i + 1][j - 1] == 1 && a[i] == a[j])[要想ai……aj这个串是回文串,ai+1……aj-1一定要是回文串并且ai要和aj相等]
- f[i][j] = 0(其他情况)
我们要注意初始条件,包含一个字母和零个字母的情况都是回文串,所以f[i][i] = 1, f[i][i - 1] = 1。
石子合并
问题描述:在一个园形操场的四周摆放N堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的2堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。试设计出1个算法,计算出将N堆石子合并成1堆的最小得分和最大得分。
和之前NOIP经典和合并石子不同,合并石子那题是每次可以选任意两堆合并,而这道题每次只可以选择相邻的两堆石子合并。这道题带环不是很好操作,所以为了简化问题,我们先先考虑没有环的情况。
对于没有环的情况其实很简单,我们设 f[i,j]表示合并i到j的所有石子的得分,我们考虑最后一次合并一定是两堆石子合并,而这两堆石子肯定一个是左半边的集合一个是右半边的集合,所以我们枚举分界点k就有f[i,j] = max(f[i][j], f[i][k] + f[k + 1][j] + sum[i][j])。在这里sum[i][j] 表示i到j的石子的价值和,我们也可以前缀和实现 sum[i]表示前i个石子的价值,那么我们需要的就是sum[j] – sum[i - 1]。这样就做完啦。
但是现在有环!那我们又该怎么做呢?我们有两种方法,一种是可以通过取模的方法把它变成循环的,这种比较麻烦我们来看看另一种——将序列加倍:比如我们序列'1234'可以变成‘12341234’,就可以完全用链的方法解决了!我们最后只要在枚举开头i在f[i][i+n](n为原始序列长度)当中取一个最大值就是我们的答案啦。记得边界: f[i][i] = 0。其实我们这个双倍再截取[i, i + n]的操作本质上就是在枚举断点。这就很区间动态规划。
凸多边形的三角拆分
问题描述:给定一个具有 N(N <=50)个顶点(从 1 到 N 编号)的凸多边形,每个顶点的权均已知。问如何把 这个凸多边形划分成 N-2 个互不相交的三角形,使得这些三角形顶点的权的乘积之和最小。
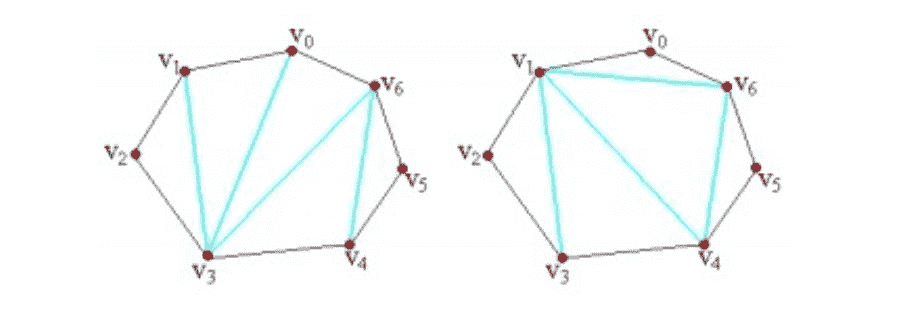
我们还是沿用区间动态规划的思路,我们设设f[i][j](i <j)表示从顶点I 到顶点J 的凸多边形三角剖分后所得到的最大乘积。我们知道ij这条边一定是某个三角形的一条边,所以我们可以枚举一点k,让i,j,k组成一个三角形,这样我们剩下的就是[i,k]和[k,j]。所以我们可以很轻易地得到下面的动态转移方程:
f[i][j]=Minf[i][k]+f[k][j]+s[i]*s[j]*s[k](i<k<j)
显然,目标状态为: f[1][n]。
这样我们就完成了这道题。
田忌赛马
题目描述:我国历史上有个著名的故事: 那是在2300年以前。齐国的大将军田忌喜欢赛马。他经常和齐王赛马。他和齐王都有三匹马:常规马,上级马,超级马。一共赛三局,每局的胜者可以从负者这里取得200银币。每匹马只能用一次。齐王的马好,同等级的马,齐王的总是比田忌的要好一点。于是每次和齐王赛马,田忌总会输600银币。
田忌很沮丧,直到他遇到了著名的军师――孙膑。田忌采用了孙膑的计策之后,三场比赛下来,轻松而优雅地赢了齐王200银币。这实在是个很简单的计策。由于齐王总是先出最好的马,再出次好的,所以田忌用常规马对齐王的超级马,用自己的超级马对齐王的上级马,用自己的上级马对齐王的常规马,以两胜一负的战绩赢得200银币。实在很简单。
如果不止三匹马怎么办?现在给你田忌和齐王的n匹马的速度值,速度值高的马将会在比赛中获胜如果速度值一样则视为平局。这个问题很显然可以转化成一个二分图最佳匹配的问题。把田忌的马放左边,把齐王的马放右边。田忌的马A和齐王的B之间,如果田忌的马胜,则连一条权为200的边;如果平局,则连一条权为0的边;如果输,则连一条权为- 200的边……如果你不会求最佳匹配,用最小费用最大流也可以啊。
然而,赛马问题是一种特殊的二分图最佳匹配的问题,上面的算法过于先进了,简直是杀鸡用牛刀。现在,就请你设计一个简单的算法解决这个问题。
看到这道题,相信你也和我一样,觉得可以贪心?我们来一组数据,田忌:92 65 33 17,齐王 97 60 22 20。我们先将两边的马从高到低排序。第一场齐王派出最强的马97,我们田忌就算派出最强的马也是输,所以一定输的情况下我们就派出最弱的马也就是17去迎战。到了第二场,齐王派出剩下的最强的马也就是60,这时我们就可以派出最强的马92去迎战。有的同学可能会问了,为什么不派刚好比60大的60去呢。派92不是浪费吗?其实这两匹马派谁去都是等价的。因为已经排序过了后面齐王派出的马一定小于等于60,所以65和92到后面只要出场就是稳赢。而为了方便我们就派出田忌最强的马92去迎战。
到这里相信你已经看出我们的策略了。每次我们拿齐王最强的马和田忌最强的马比较,如果田忌能赢就派上最好的马,如果不能赢就派上最差的马。这看起来是正确的。
的确,在没有平局的情况下,这种做法完全没有问题。但一旦出现平局,我们是派最好的马还是最弱的马呢?假如我们是平局时派最好的马,那我们来看看这组数据田忌 : 3 2 1,齐王 : 3 2 1。如果平局我们还派上最好的马最后的答案就是0,但实际上我们可以1-3,3-2,2-1(a-b表示田忌派出速度为a的马齐王派出速度为b的马)这样酒囊拿到400-200=200硬币,显然打平时一味派上最好的马不是最优的。
那有没有可能在打平是派上最差的马呢?假如我们是平局时派最好、差的马,那我们来看看这组数据田忌 : 3 2,齐王 : 3 1。那我们两局就是2-3和3-1,就是一赢一输,得到答案是0。但如果此时我们在平局时派出最强的马那我们两局就是3-3和2-1,就是一赢一平,得到答案是200,显然打平时一味派上最差的马也不是最优的。
我们接着来分析。总结起来就是:田忌能赢就赢,如果一定输就要输的最惨,如果能打平就出现打平和输两种情况。所以:田忌出马不是出最强的,就是出最弱的。所以我们可以先将田忌和齐王的马按从大到小顺序排序且默认齐王按从大到小出马(齐王出马的顺序不影响田忌的策略和得分)
接着我们用f[i][j]表示田忌区间[i, j]的马比下去的最优得分,则我们可以得到状态转移方程f[i][j]=max(f[i+1][j]+cost(i,k),f[i][j-1]+cost(j,k))。其中k表示齐王当前出的马,cost(i,k)是田忌第i匹马与齐王第k匹马相比的结果。
然后要考虑边界,边界是什么?边界一定是i=j时的值,f[i][i]又等于什么呢?由于齐王是从大到小派出马的,当区间为[1, n]的时候齐王出的马是第一匹,随着区间长度的减少,齐王的出的马变成了后面的,于是——f[i][i] 是齐王出最弱那匹马的时候的与田忌第i匹马相比的收益。
所以我们的田忌赛马就顺利用区间动态规划解决啦。
结语
通过这篇BLOG,相信你已经对区间动态规划有了一个系统的了解,也通过例题了解了区间动态规划的大致套路。最后希望你喜欢这篇BLOG!