昨天打了一下2005年的SCOI，虽然已经是十多年前的省选题了，但是很多题目还是不能一次AC（我太菜了QwQ），下面就让我来讲讲这套题的解法吧

T1 超级格雷码

题目描述：

Description:
著名的格雷码是指2n个不同n位二进制数（即0~2n-1，不足n位在前补零）的一个排列，这个排列满足相邻的两
个二进制数的n位数字中最多只有一个数字不同（例如003和001就有一个数位不同，而003和030有两个数位不同，
不符合条件）。例如n=2时，(00,01,11,10)就是一个满足条件的格雷码。 所谓超级格雷码就是指Bn个不同的n位B
进制数的排列满足上面的条件。 任务：给出n和B（2≤B≤36, 1≤Bn≤65535），求一个满足条件的格雷码。对于
大于9的数位用A~Z表示（10~35）。

Input
只有一行，为两个整数n和B。

Output
一共Bn个行，每行一个B进制数，表示你所求得的符合条件的排列

Sample Input
2 2

Sample Output
00
01
11
10

AC解法：
这道题的思路就是很经典的打表找规律，首先我们先可以打出一个3,3的表：

000
100
200
210
110
010
020
120
220
221
121
021
011
111
211
201
101
001
002
102
202
212
112
012
022
122
222

然后我们发现，对于从左往右数的任意第i位，在第i位不变的一个序列中（见下图），他的前一位（也就是i-1位）是按顺序或者逆序排列的，那么究竟是顺序还是逆序呢？

1.PNG

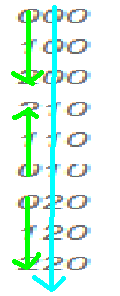
通过观察我们发现：
当从左往右数的任意第i位为偶数时，则第i-1位是相对于第i位的枚举顺序递增枚举的（比如第二列为0时，前一列为【0,1,2】（第一个绿色箭头））,即若第i位为顺序，则i-1位为顺序，若第i位为逆序，则i-1位为逆序；

反之当第i位为奇数时，则第i-1位是第i位的枚举顺序递减枚举的（比如第二列为2时，前一列为【2,1,0】（第二个绿色箭头）），即若第i位为顺序，则i-1位为逆序，若第i位为逆序，则i-1位为顺序。

所以程序就很显然了：

程序部分：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int n,b;
int a[1100];

int build(int k,int t)
{
    if(k==0)
    {
        for(int i=1;i<=n;i++)
        if(a[i]<10)printf("%d",a[i]);
        else printf("%c",a[i]-10+'A');

        printf("\n");
        return 0;
    }

    if(t==1)
    {
        for(int i=0;i<b;i++)
        {
            a[k]=i;
            if(i%2==1)build(k-1,0);
            else build(k-1,1);
        }
    }
    else
    {
         for(int i=b-1;i>=0;i--)
         {
            a[k]=i;
            if(i%2==1)build(k-1,1);
            else build(k-1,0);
         }
    }
}

int main()
{
    scanf("%d%d",&n,&b);
    memset(a,sizeof(a),0);
    build(n,1);
    return(0);
}

T2 栅栏

题目描述：

Description

农夫约翰打算建立一个栅栏将他的牧场给围起来，因此他需要一些特定规格的木材。于是农夫约翰到木材店购
买木材。可是木材店老板说他这里只剩下少部分大规格的木板了。不过约翰可以购买这些木板，然后切割成他所需
要的规格。而且约翰有一把神奇的锯子，用它来锯木板，不会产生任何损失，也就是说长度为10的木板可以切成长
度为8和2的两个木板。你的任务：给你约翰所需要的木板的规格，还有木材店老板能够给出的木材的规格，求约翰
最多能够得到多少他所需要的木板。

Input

　>　第一行为整数m(m<= 50)表示木材店老板可以提供多少块木材给约翰。紧跟着m行为老板提供的每一块木板的长
度。接下来一行(即第m+2行)为整数n(n <= 1000)，表示约翰需要多少木材。接下来n行表示他所需要的每一块木板
的长度。木材的规格小于32767。（对于店老板提供的和约翰需要的每块木板，你只能使用一次）。

Output

　>　只有一行，为约翰最多能够得到的符合条件的木板的个数。

Sample Input

4
30
40
50
25
10
15
16
17
18
19
20
21
25
24
30

Sample Output
7

HINT
25切出 21 30切出 20 40切出 19、18 50切出 15、16、17

AC解法：

首先看到这道题，就觉得正着做很难做，所以我们就考虑能不能从侧面做？

当然是可以的，那么如何从侧面做呢？很经典的做法，我们可以二分我们能得到的符合条件的木板的个数，若当次二分到k，接下来就是如何判断能否满足前k小的需求了。

正常来说，我们的思路就是DFS枚举用第i块木板来满足第j个需求。但是若是裸的DFS，肯定超时。那么我们只要看能否满足前k小的全部所需木板就行了。

因为贪心的来想一下，对于任意一次需求的木棍，若能满足大的木板，就必定能满足小的木板，所以我们只需要判断小的木板能否满足就行了（若小的无法满足，大的也一定能满足）

所以DFS的时候是按照需要的木棍从大到小的顺序一层一层搜，每一层上是按照从小到大的顺序枚举提供的木棍。（当然枚举的时候已经不一定是从小到大了，有些木棍已经被截掉了一些。）

要使用两个有效的剪枝：

1）如果下一层的木棍和这一层的木棍等长，就从这一层木棍枚举到的提供的木棍开始枚举，因为前面的都是不可以的。

2）当一根木棍被截掉一段之后小于最小的需要的木棍，那么它就废掉了，记录当前废掉的木棍总长Rest，如果Rest + 1到mid所有木棍的总长 > 提供的所有木棍总长，那么就返回 false。

具体来看程序吧：

程序部分：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int a[1000],b[11000],c[11000];
int i,j,k,m,n,o,p,js,jl,l,r,mid,tot,w;

bool pd(int x,int last)//x表示木板个数，last表示从哪个木板开始考虑(切割)
{
    int i;bool fg;
    if(w>tot-c[mid])return(false);
    if(x==0)return(true);

    for(i=last;i<=m;i++)
    if(a[i]>=b[x])
    {
        a[i]=a[i]-b[x];//切掉这块
        if(a[i]<b[1])w=w+a[i];//如果比最小的一块还要小，则算作废料

        if(b[x-1]==b[x]) fg=pd(x-1,i);//回溯
        else fg=pd(x-1,1);

        if(a[i]<b[1])w=w+a[i];
        a[i]=a[i]+b[x];

        if(fg==true)return(true);
    }
    return(false);

}

int main()
{
    scanf("%d",&m);
    for(int i=1;i<=m;i++)
    {
        scanf("%d",&a[i]);
        tot=tot+a[i];
    }
    sort(a+1,a+m+1);

    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&b[i]);

    }
    sort(b+1,b+n+1);
    for(int i=1;i<=n;i++)c[i]=c[i-1]+b[i];

    while (c[n]>tot) n--;  
    l=0;r=n;
    while(r-l>1)
    {
        w=0;
        mid=(l+r)/2;
        if(pd(mid,1)==true)l=mid;
        else r=mid-1;
    }
    w=0;
    if(pd(r,1)==true)printf("%d",r);
    else printf("%d",l);
    return 0; 
}

T3 繁忙的都市

题目描述：

Description

城市C是一个非常繁忙的大都市，城市中的道路十分的拥挤，于是市长决定对其中的道路进行改造。城市C的道
路是这样分布的：城市中有n个交叉路口，有些交叉路口之间有道路相连，两个交叉路口之间最多有一条道路相连
接。这些道路是双向的，且把所有的交叉路口直接或间接的连接起来了。每条道路都有一个分值，分值越小表示这
个道路越繁忙，越需要进行改造。但是市政府的资金有限，市长希望进行改造的道路越少越好，于是他提出下面的
要求： 1． 改造的那些道路能够把所有的交叉路口直接或间接的连通起来。 2． 在满足要求1的情况下，改造的
道路尽量少。 3． 在满足要求1、2的情况下，改造的那些道路中分值最大的道路分值尽量小。任务：作为市规划
局的你，应当作出最佳的决策，选择那些道路应当被修建。

Input

第一行有两个整数n,m表示城市有n个交叉路口，m条道路。接下来m行是对每条道路的描述，u, v, c表示交叉
路口u和v之间有道路相连，分值为c。(1≤n≤300，1≤c≤10000)

Output

两个整数s, max，表示你选出了几条道路，分值最大的那条道路的分值是多少。

Sample Input
4 5
1 2 3
1 4 5
2 4 7
2 3 6
3 4 8

Sample Output
3 6

AC解法：

这应该是这套题目最水的一道题目了吧，思路有两种：

首先，因为图一定是联通的，所以若要改造的道路尽量少，最后出来的路径一定是一棵树。想到树，想到最长边最短，想到什么？

二分！（划掉）当然是最小生成树啊，所以只要跑一遍裸的最小生成树就AC了。

当然，这当然不是最简单的解法了，因为我们知道路径条数是n-1，所以我们只要求出这颗最小生成树最长边就行了，所以就很简单了呀——我们对边从小到大排序，再一条条边加进去，直到整幅图联通就行了。至于图是否联通，只要写个并查集就行了（记得路径压缩！！！）

程序部分：

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
    int x,y,sum;
}a[100000];

int f[310],g[310],i,j,k,m,n,o,p,js,jl,x,y;

int comp(node x,node y)
{
    if(x.sum<y.sum)return(true);
    else return(false);
}

int find(int x)//并查集+路径压缩
{
    int p=x,t;  
    while(f[p]!=p)p=f[p];
    while(x!=p){t=f[x];f[x]=p;x=t;}//路径压缩 
    return x;  
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].sum);
    sort(a+1,a+m+1,comp);
    for(int i=1;i<=n;i++)
    {
        g[i]=1;
        f[i]=i;
    }
    printf("%d ",n-1);
    for(int i=1;i<=m;i++)
    {
        x=find(a[i].x);
        y=find(a[i].y);
        if(x!=y)
        {
            f[x]=y;
            g[y]=g[y]+g[x];
            if(g[y]==n)
            {
                printf("%d",a[i].sum);
                exit(0);
            }
        }
    }

    return 0;
}

T4 最大子矩阵

题目描述：

Description

这里有一个n*m的矩阵，请你选出其中k个子矩阵，使得这个k个子矩阵分值之和最大。注意：选出的k个子矩阵
不能相互重叠。

Input

第一行为n,m,k（1≤n≤100,1≤m≤2,1≤k≤10），接下来n行描述矩阵每行中的每个元素的分值(每个元素的
分值的绝对值不超过32767)。

Output

只有一行为k个子矩阵分值之和最大为多少。

Sample Input
3 2 2
1 -3
2 3
-2 3

Sample Output
9

AC解法：

这道题咋一看，好像很高级，不会做，什么数据结构都用不上；再看一眼，呀！1≤m≤2！所以只要分类讨论就好了；

当m=1时，直接DP，设f【i】【k】为前i位分k个段可以到达的最大收益，g【i】为前i位的前缀和；那么动态规划方程就很显然了：
f[j][k]=my_max(f[j][k],f[i-1][k-1]+g[j]-g[i-1]);

当m=2时，设f【i】【j】【k】为第1列到第i位，第2列到第j位，分k个段可以到达的最大收益，g【i】【j】为第j列前i位的前缀和，我们考虑三种情况（如下图）：

2.PNG

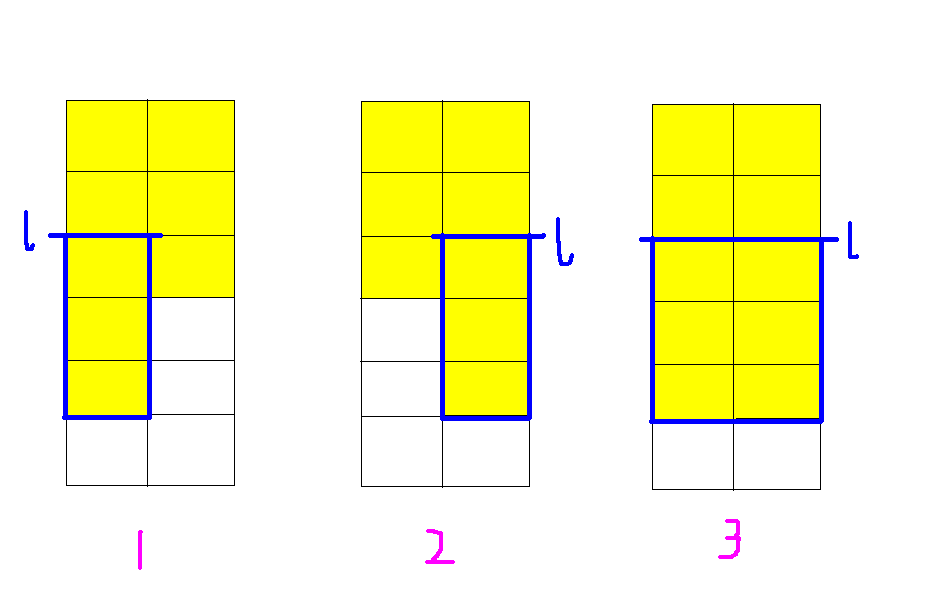
就是先对于每一个a【i】【j】【k】，可以从a【l】【j】【k-1】和a【i】【l】【k-1】转移过来（如图1,2）；同理当i==j的时候，可以从a【l】【l】【k】转移过来。

所以动态规划的方程就呼之欲出了：

for(int ll=1;ll<=i;ll++)f[i][j][k]=my_max(f[i][j][k],f[ll-1][j][k-1]+g[i][1]-g[ll-1][1]);
            for(int ll=1;ll<=j;ll++)f[i][j][k]=my_max(f[i][j][k],f[i][ll-1][k-1]+g[j][2]-g[ll-1][2]);
            if(i==j)for(int ll=1;ll<=i;ll++)f[i][j][k]=my_max(f[i][j][k],f[ll-1][ll-1][k-1]+g[j][2]-g[ll-1][2]+g[i][1]-g[ll-1][1]);

程序部分

#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int f[1100][1100][11];
int a[11000][10],g[11000][10];
int i,j,k,m,n,o,p,js,jl,jk,kk,ma,ll;
int my_max(int x,int y)
{
    if(x>y)return(x);
    else return(y);
}
int main()
{
    scanf("%d%d%d",&n,&m,&kk);
    memset(f,-63,sizeof(f));
    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
    {
        scanf("%d",&a[i][j]);
        g[i][j]=g[i-1][j]+a[i][j];
    }

    for(int i=0;i<=n;i++)
    for(int j=0;j<=n;j++)
    f[i][j][0]=0;
    if(m==1)
    {
        ma=-214748364;
        for(i=1;i<=n;i++)
        for(j=i;j<=n;j++)
        for(k=1;k<=kk;k++)
        {
            f[i][1][k]=my_max(f[i][1][k],f[i-1][1][k]);
            f[j][1][k]=my_max(f[j][1][k],f[i-1][1][k-1]+g[j][1]-g[i-1][1]);
            if(k==kk)if(f[j][1][k]>ma)ma=f[j][1][k];
        }
        printf("%d",ma);
    }

    else
    {
        ma=-214748364;
        for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        for(int k=1;k<=kk;k++)
        {
            f[i][j][k]=my_max(f[i-1][j][k],f[i][j-1][k]);
            for(int ll=1;ll<=i;ll++)f[i][j][k]=my_max(f[i][j][k],f[ll-1][j][k-1]+g[i][1]-g[ll-1][1]);
            for(int ll=1;ll<=j;ll++)f[i][j][k]=my_max(f[i][j][k],f[i][ll-1][k-1]+g[j][2]-g[ll-1][2]);
            if(i==j)for(int ll=1;ll<=i;ll++)f[i][j][k]=my_max(f[i][j][k],f[ll-1][ll-1][k-1]+g[j][2]-g[ll-1][2]+g[i][1]-g[ll-1][1]);
            if(k==kk)if(f[i][j][k]>ma)ma=f[i][j][k];
        }
        printf("%d",ma);
    }
    return 0;
}

结语

总的来说，这套题的难度就在普及组和提高组左右，细细想想还是可以AK的，希望你喜欢这篇题解！
3.PNG

Last modification：July 12th, 2018 at 05:27 pm
© 允许规范转载
If you think my article is useful to you, please feel free to appreciate