我们终于来到了动态规划专题啦。在接下来的几篇BLOG中，我将会由浅入深，逐一讲解现在常见的几种动态规划类型。由于动态规划更多的是推导的过程而不是代码部分讲解，所以在接下来的几部分我也会拿出更多的经典模型结合讲解，培养同学们推方程的能力。下面就让我们进入动态规划专题的第一篇，线性动态规划入门吧！

动态规划历史

动态规划，这个看起来非常年轻的算法，其实早在1957念就被贝尔曼在《动态规划》一书中提出了。当时距离第一台电子计算机的出现仅仅过去了11年，所以当时的动态规划还不是为计算机所准备的，而是为数学家门手工列表解决动态规划问题而存在的。动态规划最为运筹学的分支，讲求的是大局观，而不像贪心那样鼠目寸光。

动态规划第一次在OI的赛场上出现可以追溯到90年代的一场IOI中的数字三角形一题，这题我们后面也会进行讲解。这道现在被视为入门的动态规划题当年却让程序设计竞赛世界最顶尖的选手抓耳挠腮。直到今日，信息学竞赛中动态规划的难度相较于三十年前已经翻了好几番。但同学们不要担心，我们会一个一个专题仔仔细细地教会你动态规划。

动态规划的引入

为了引入动态规划，让我们先来看几个大家都很熟悉的模型。

斐波那契数列

我们都知道，斐波那契数列就是满足如下规则的数列，其形如 1 1 2 3 5 8……：

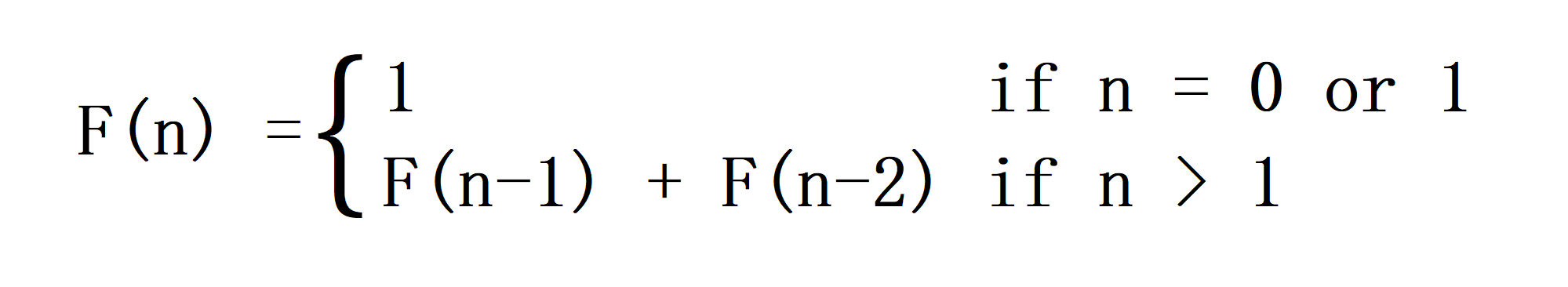
那如果我们要求斐波那契数列的第n项，我们可以怎么求解呢？首先我们可以很轻易的想到一个递归，要求第n项即f(n)，我就分别递归求出f(n - 1)和f(n - 2)，我们可以得到如下代码：

int f(int n) {
    if (n == 0 || n == 1) return 1;
    else return f(n - 1) + f(n - 2);
}

我们也可以很轻易地得到一个递推，我们知道了f(0)和f(1)，就可以算出f(2) = f(1) + f(0);算出了f(2)，就可以算出f(3) = f(2) + f(1)……这样的话我们就能依次递推出f(4), f(5)……一直到f(n)，我们可以得到如下代码：

A[0] = A[1] = 1;
for (i = 2; i <= n; i++)
    A[i] = A[i - 1] + A[i - 2];
return A[n];

然后我们同时运行这两个代码，一起跑n = 100的数据你就发现同样是求f(100)，递推的代码很快就跑出来了，而递归的算法跑了一年都还没出结果。那么这是为什么呢？

我们画一下n = 5情况下递归的算法的搜索树：

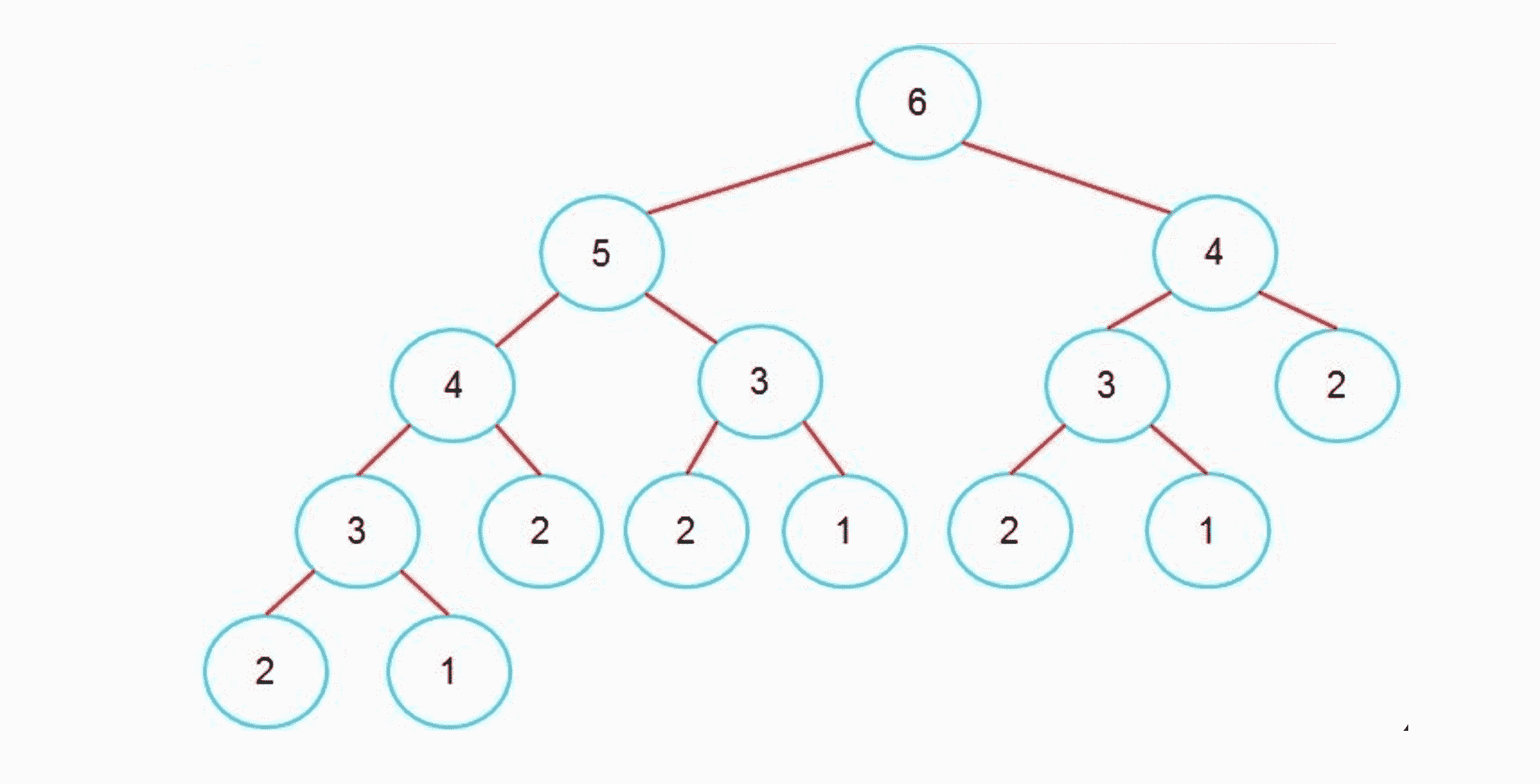
我们就发现我们进行了太多次重复计算——我们为了算f(6)，算了两次f(4)，三次f(3)，五次f(2)，我们在递归的过程中重复计算子问题给我们带来了巨大的计算空间。那我们有没有优化的方法呢？

其实是有的，要优化时间我们有个很经典的套路叫做以空间换时间。我们上述方法太慢的原因是重复计算已经计算过的子问题，那就很简单我们开一个数组把计算过的 f 值存起来就好啦，这样就能很有效地避免重复计算。而这就是我们常常说到的记忆化搜索：

int calc（int n）{
    if (f([n]!= 0) return f[n];
    return (f[n] =calc(n-1) + calc(n-2));
}

经过这样的优化我们的每个f值只计算一次所以我们的时间复杂度就是O(n)的。可能有的同学是第一次接触记忆化搜索，那我就在这多讲几句吧。 记忆化搜索，顾名思义，就是带有记忆化的搜索。也就是说，用数组等将已经算过的东西记录下来在下一次要使用的直接用已经算出的值，避免重复运算，去掉的重复的搜索树。经过记忆化搜索，我们的搜索树就从刚刚那样变成了下面这样：

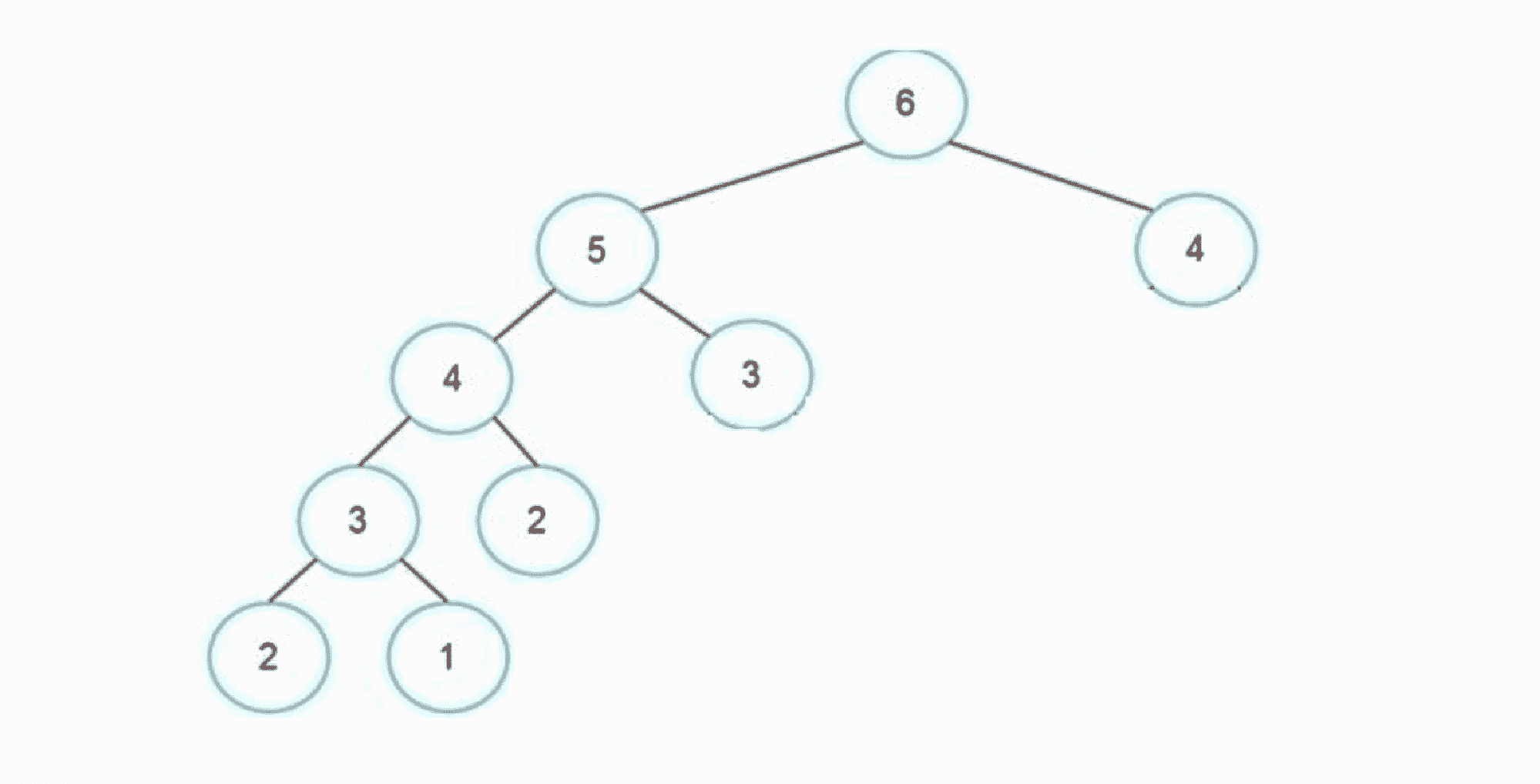
其实求斐波那数列看起来是简单的递推和递归，我们实际上也可以把它理解成是动态规划——通过已知状态转移出当前状态。在现实生活中我们写动态规划的时候常用的写法其实也是这两种——类似于递推的循环写法和类似于记忆化搜索。

走楼梯问题

我们接着再来看另一个很经典的模型，有一人要爬n阶的楼梯，他一次可以爬1阶或2阶，问要爬完这n阶楼梯，共有多少种方法？

其实这道题也不难，我们可以这样去考虑。假设我们现在在第n阶阶梯上，显然，我们上一步是在n-1阶或者n-2阶，根据分类加法原理，我们可以知道，第n阶的方法=n-1阶的方法+n-2阶的方法。同样的，对于n-1阶和n-2阶我们也可以用类似的方法进行求解。而当我们求到1阶和2阶的时候，显然方法种数分别为1、 2。所以如果f[i]表示爬到第i阶的方法数，那么f[1]=1 f[2] = 2 且 f[i] = f[i - 1]+ f[i - 2]。

是不是看起来非常熟悉？没错这也是一个斐波那契数列！所以我们用上面的方法求解就好了。

蜂巢问题

我们再来看一个类似的问题：有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房，不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。其中，蜂房的结构如下所示:

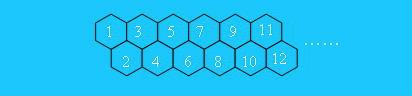
这题的难点是观察出式子。通过观察我们发现，对于任意的蜂房i，蜜蜂怎么到达蜂房i呢？只能从编号为i-1和i-2的蜂房过来，因为在i的左边只有i-1和i-2于其是相邻的。所以如果f[i]表示爬到第i个蜂房的方法数，那么f[a]=1 且 f[i] = f[i - 1]+ f[i - 2]。

这不又是一个斐波那契数列嘛，求法在第一部分应该已经讲的很清楚了。

以上三道题都是最简单最简单的动态规划，都是基于斐波那契数列这个模型。通过这一部分我相信你已经对动态规划有一点点感觉了，也知道知道方程后动态规划应该如何求解。下面就让我们来看看动态规划的原理吧！

动态规划基础知识

动态规划的原理

其实动态规划的原理只有两个——加法原理和乘法原理：

• 分类加法原理：做一件事，完成它可以有n类办法，在第一类办法中有m1种不同的方法，在第二类办法中有m2种不同的方法， ……，在第n类办法中有mn种不同的方法，那么完成这件事共有N=m1+m2+m3+…+mn种不同方法。

• 分步乘法原理：做一件事，完成它需要分成n个步骤，做第一步有m1种不同的方法，做第二步有m2种不同的方法， ……，做第n步有mn种不同的方法，那么完成这件事共有N=m1×m2×m3×…×mn种不同的方法。

其实我们动态规划要做的事情就是通过这两个原理把问题分类分步。比如很经典的数字三角形（下面会提到），我们就是按照每个点是从左上来的还是右上来的进行分类，再将三角形进行分层来按层数来分步。有个这两个原理的支持我们的动态规划才是正确的。

动态规划的概念

下面我们来看看动态规划会涉及到的一些概念及其解释。

• 动规的定义:动态规划是解决多阶段决策过程最优化问题的一种方法。
• 阶段：把问题分成几个相互联系的有顺序的几个环节，这些环节即称为阶段。
• 状态：某一阶段的出发位置称为状态。通常一个阶段包含若干状态。
• 决策：从某阶段的一个状态演变到下一个阶段某状态的选择。也就是从哪来要到哪去。
• 策略：由开始到终点的全过程中，由每段决策组成的决策序列称为全过程策略，简称策略。
• 状态转移方程：前一阶段的终点就是后一阶段的起点，前一阶段的决策选择导出了后一阶段的状态，这种关系描述了由i阶段到i+1阶段状态的演变规律，称为状态转移方程。形如：f[i] = f[i - 1]+ f[i - 2]；f[i,j]=max(f[i-1,j],f[i-1,j-1])+a[i,j]等等

比如在下图的数字三角形中，每条红线就是一个决策，红线练成的一条自顶向下的完整路线就是策略：

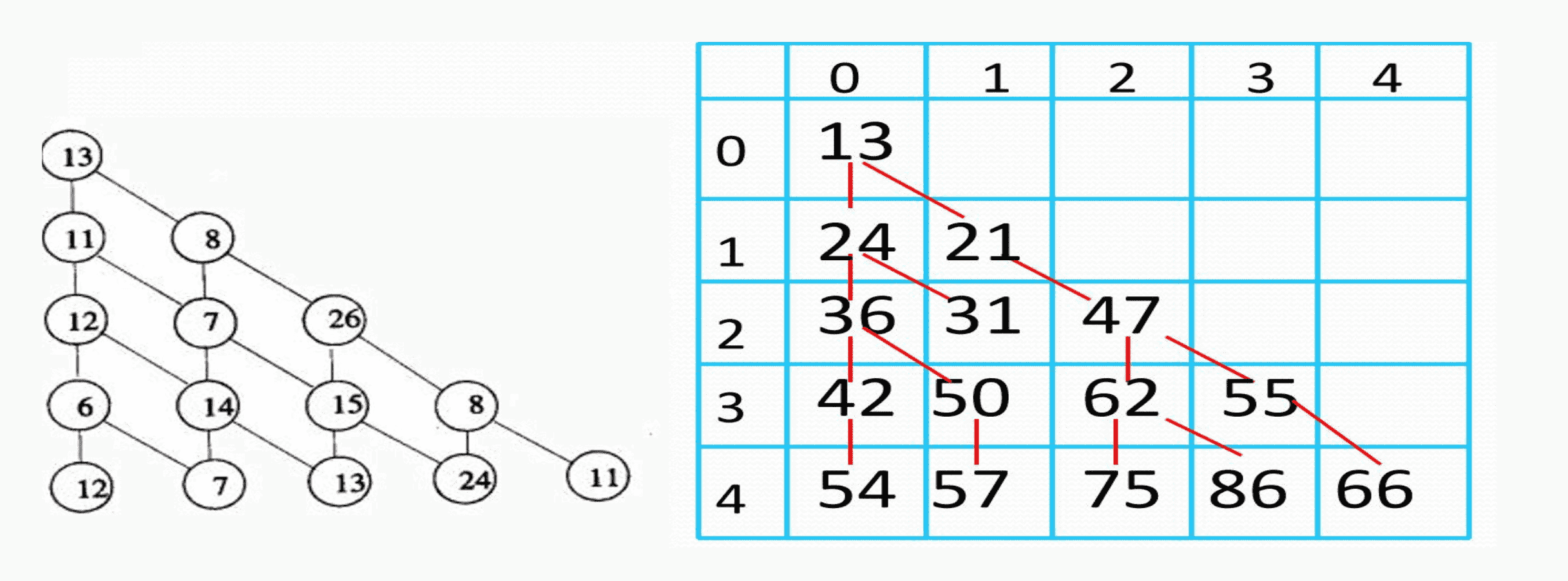
动态规划适用的基本条件

不是每道题都可以使用动态规划的，要想使用动态规划，题目要满足几个很重要的条件。

• 具有相同子问题
  首先，题目要满足具有相同子问题。我们必须要保证这个问题能够分解出几个子问题，并且能够通过这些子问题来解决这个问题。其次，将这些子问题做为一个新的问题，它也能分解成为相同的子问题进行求解。也就是说，假设我们一个问题被分解为了A,B,C三个部分，那么这A,B,C分别也能被分解为A’,B’,C’ 三个部分，而不能是D,E,F三个部分。

• 满足最优子结构
  其次题目要满足最优子结构。也就是说问题的最优解包含着它的子问题的最优解。即不管前面的策略如何，此后的决策必须是基于当前状态（由上一次决策产生）的最优决策。比如我们来举一个反例，假如对于下面这幅图，我们要求解1到4的模4意义下的最短路，也就是说我们要找出从第1点到第4点的一条路径，要求路径长度mod 4的余数最小。：
  此时如果我们每步都取最优的路，则1到2取0，2到3取1，3到4取1答案就是2。看起来很正确，但是如果我们1到2取1，2到3取1，3到4取2答案就是0（4%4=0）。所以这道题就不满足最优子结构。

• 满足无后效性
  最后题目一定要满足无后效性。“过去的步骤只能通过当前状态影响未来的发展，当前的状态是历史的总结”。这条特征说明动态规划只适用于解决当前决策与过去状态无关的问题。状态，出现在策略任何一个位置，它的地位相同，都可实施同样策略，这就是无后效性的内涵.这是动态规划中极为重要的一点，如果当前问题的具体决策，会对解决其它未来的问题产生影响，如果产生影响，就无法保证决策的最优性。

就和谈恋爱一样，一定要把历史交代清楚，要不然就算刚开始的时候再恩爱再合适到后面都会出现不信任从而产生情感裂缝。换句话说动态规划要求和我们人一样就是不能有历史遗留问题。有问题就想办法用状态表示，千万不能隐瞒一些状态！

做动态规划的一般步骤

第一步，结合原问题和子问题确定状态：（我是谁？我在哪？）

我们需要明确题目在求什么？要求出这个值我们需要知道什么？什么是影响答案的因素？如何描述状态？（一维描述不完就二维，二维不行就三维四维。）状态的参数一般有：

描述位置的：前(后)i单位，第i到第j单位，坐标为(i,j)，第i个之前（后）且必须取第i个等
描述数量的：取i个，不超过i个，至少i个等
描述对后有影响的：状态压缩的，一些特殊的性质

第二步，确定转移方程：（我从哪里来？ /我到哪里去？）

为了确定转移方程，我们一般的步骤如下：

1. 检查参数是否足够；
2. 分情况： 最后一次操作的方式，取不取，怎么样取——前一项是什么
3. 初始边界是什么。
4. 注意无后效性。比如说，求A就要求Ｂ，求Ｂ就要求Ｃ，而求Ｃ就要求Ａ，这就不符合无后效性了。

根据状态枚举最后一次决策（即当前状态怎么来的）一般就可确定出状态转移方程啦！

第三步，考虑需不需要优化：（空间优化？/时间优化？）
一般来说动态规划的优化分为空间优化和时间优化。对于空间我们最经常讨论能不能滚动数组？需不需要离散化？之类的。而对于时间优化，我们最常讨论的是能不能通过矩阵快速幂进行加速？之类的。

第四步，确定编程实现方式：（递推？/记忆化搜索？)
在很多简单的问题上，递推和记忆化搜索的思路都很简单也很好写。但实际上对于许多稍微复杂一些的问题，往往记忆化搜索的难度会远远小于递推。所以如果在考场上想不到递推的写法，不如另辟蹊径想想记忆化搜索吧！

常见线性动态规划模型

数字三角形

设有一个三角形的数塔，顶点结点称为根结点，每个结点有一个整数数值。从顶点出发，可以向左走，也可以向右走，如下图所示。问题：当三角形数塔给出之后，求从第一层到达底层的路径最大值。

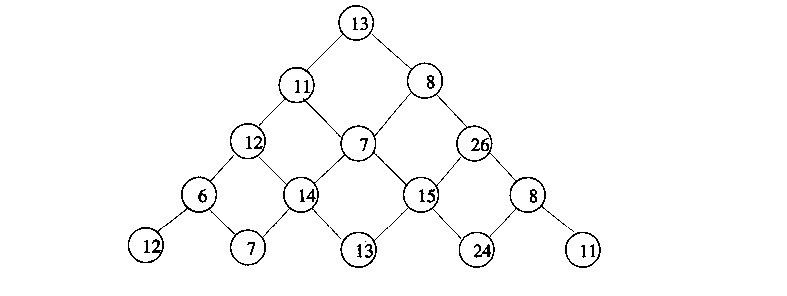
这道题应该也算线性动态规划的经典题目了，这题第一次出现在IOI赛场上的时候完成情况并不理想，换句话说如果你学懂了这题你就有IOI水平了（滑稽）。

让我们来分析一下这道题。首先这个三角形长成上面这个形状我们是不太好存储的。所以我们首先要将三角形向左压缩一下：

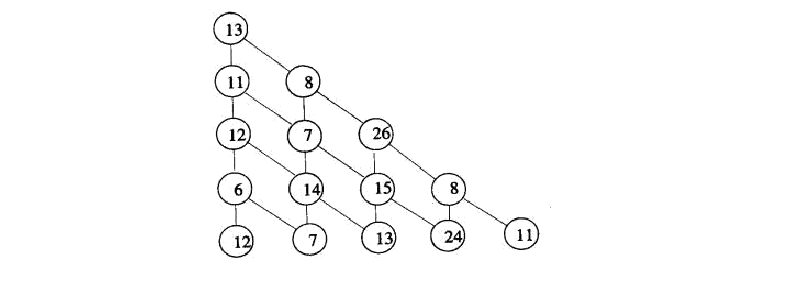
这样我们每个点就从往左下走和往右下走变成了往正下方走和往右下方走。接着我们考虑如何表达状态，显然在这一题中要表示的只有位置信息。我们设a[i][j]为从上往下数第 i 行从左往右数第 j 个点的权值，F[i][j]为从最上面的顶点到达从上往下数第 i 行从左往右数第 j 个点时的最大值。这样我们最后的答案就是F[n][1]到F[n][n]中的最大值。

那我们如何转移呢？

我们对于F[i][j]，我们考虑它能从哪里来，很显然只能从左上的点和正上的点这两个点转移过来。所以很容易就能发现到达从上往下数第 i 行从左往右数第 j 个点的最大值等于从上往下数第 i - 1 行从左往右数第 j - 1 个点的最大值和从上往下数第 i - 1 行从左往右数第 j 个点的最大值之间取最大值再加上从上往下数第 i 行从左往右数第 j 个点自己本身的权值。写出方程F[i][j] = max(F[i - 1][j - 1], F[i - 1][j]) + a[i][j]：

实现的话我们使用递推就好啦。这样这题就写完啦：

for(int i = 0; i < n; i++) {
    for(int j = 0; j <= i; j++) {
    f[i][j] = max(f[i - 1][j], f[i - 1][j - 1]) + a[i][j];
    }
}

最后我们对最后一行的f值进行扫描，最大的那一个即是结果；也可以倒着走（从下往上）这样f[1][1]就是结果了。

路径条数问题

N*M的棋盘上左上角有一个过河卒，需要走到右下角。行走的规则：可以向下、或者向右。现在要求你计算出从左上角能够到达右下角的路径的条数，如下图：

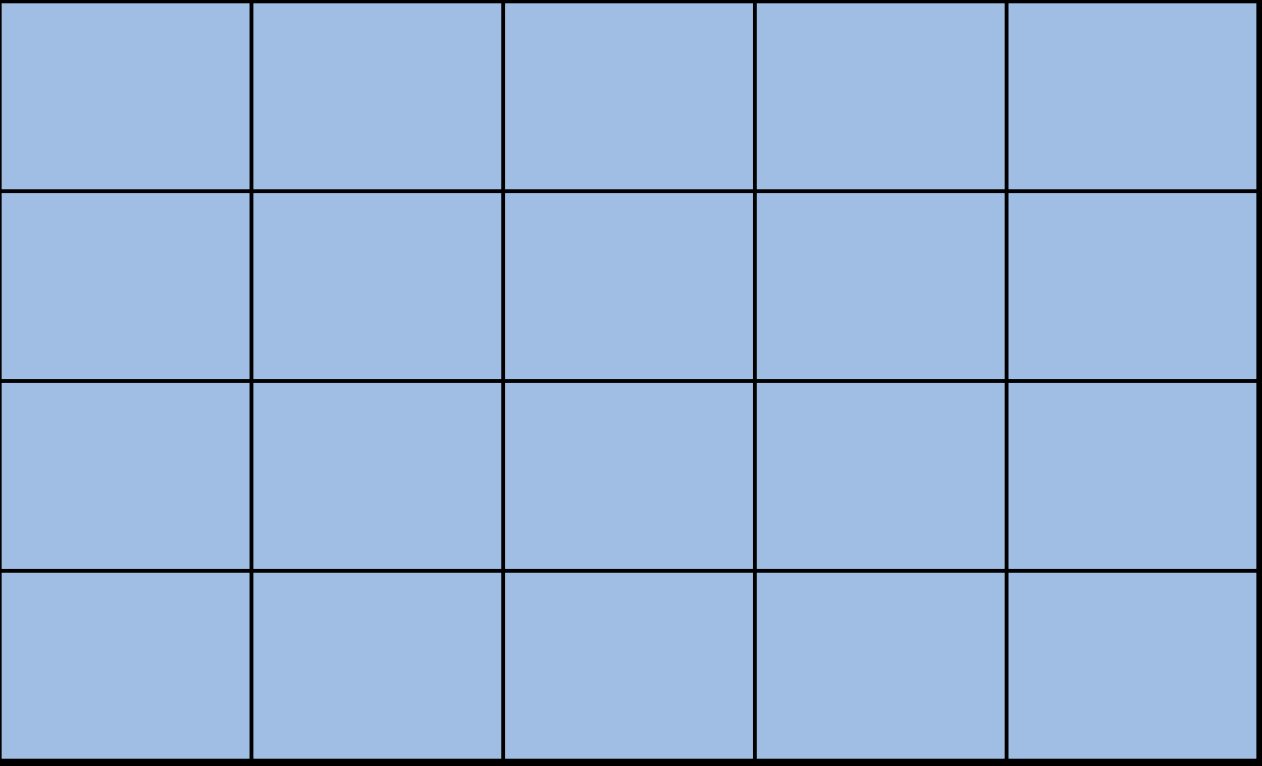
这一题题目比上一题更加复杂，无法一眼看出解法，所以就让我们来运用刚刚学到的动态规划的步骤一步一步进行解答。
第一步：确定状态——原问题是什么？子问题是什么？
原问题：从(0,0)走到(n,m)的路径数
子问题：从(0,0)走到(i,j)的路径数
f[i][j]表示从左上角走到 (i,j)点的路径条数
第二步：确定状态转移方程和边界
我们知道每个点只能从左边和上面的格点到达，所以有：
f[i][j] = f[i-1][j] + f[i][j-1]
f[1][i] =f[i][1]= 1;
第三步：考虑是否需要优化
第四步：确定实现方法
直接使用递推就好了。 (本题其实可以直接用排列组合求)这题还有一个很有意思的点就是如果我们把填好的f[i][j]旋转一下你就发现这其实是一个杨辉三角。

这样我们就完成了这道题。

过河卒

棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上C点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示， A点(0, 0)、 B点(n, m)(n, m为不超过20的整数)，同样马的位置坐标是需要给出的。
现在要求你计算出卒从A点能够到达B点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

这一题题目和上一题类似，只不过加入了马的存在，现在就让我们继续运用动态规划的步骤一步一步进行解答。
第一步：确定状态——原问题是什么？子问题是什么？
原问题：从(0,0)走到(n,m)的路径数
子问题：从(0,0)走到(i,j)的路径数
f[i][j]表示从A点走到 (i,j)点的路径条数
第二步：确定状态转移方程和边界
g[i][j] = 0((i,j)不是马的控制点)/1((i,j)是马的控制点)
我们知道每个点只能从左边和上面的格点到达，所以有：
f[i][j] = f[i-1][j] + f[i][j-1] (g[i][j] == 0)
f[i][j] = 0 (g[i][j] == 1)
边界条件：f[0][0] = 1;
第三步：考虑是否需要优化
第四步：确定实现方法
直接使用递推就好了。

使用动态规划四步法是不是更加简单了呢？

传球游戏

n个同学站成一个圆圈，其中的一个同学手里拿着一个球，当老师吹哨子时开始传球，每个同学可以把球传给自己左右的两个同学中的一个（左右任意），当老师再次吹哨子时，传球停止。
聪明的小蛮提出一个有趣的问题：有多少种不同的传球方法可以使得从小蛮手里开始传的球，传了m次以后，又回到小蛮手里。两种传球的方法被视作不同的方法，当且仅当这两种方法中，接到球的同学按接球顺序组成的序列是不同的。比如有3个同学1号、 2号、 3号，并假设小蛮为1号，球传了3次回到小蛮手里的方式有1->2->3->1和1->3->2->1，共2种。

这题也很有意思，我们还是使用动态规划的解题步骤一步一步进行解答。

第一步：确定状态——原问题是什么？子问题是什么？
原问题：从1开始传球第m步球回到1的方法数
子问题：从1开始传球第i步球到达j的方法数
f[i][j]表示第i次传球之后球在第j个人手上的方法数
第二步：确定状态转移方程和边界
一般来说在考虑方程的时候我们可以考虑最后一步的转移，我们要统计的是第m步后回到1的方法数，那如何让m步后会到1呢？就是要让m-1步后到达2或者n才行，所以f[m][1] = f[m-1][2] + f[m-1][n]。我们进行推广就知道每一步的球只可能是从它的左边或者右边来，所以我们有：
f[i][j] = f[i-1][j-1] + f[i-1][j+1]
f[0][1] = 1;
注意由于是一个环， j=1 时 左边（j-1） 为n， j=n 时 右边（j+1）为1
第三步：考虑是否需要优化
第四步：确定实现方法
这题递推的实现就不是特别方便了，还是考虑记忆化搜索会更加简单。

最长不下降子序列

设有一个正整数的序列： b1,b2,…， bn，对于下标i1<i2<…＜ im，若有bi1≤bi2≤…≤bim 则称存在一个长度为m的不下降序列。
例如，下列数列 13 7 9 16 38 24 37 18 44 19 21 22 63 15 对于下标i1=1， i2=4， i3=5， i4=9， i5=13，满足13＜ 16＜ 38＜ 44＜ 63,则存在长度为5的不下降序列。
但是，我们看到还存在其他的不下降序列: i1=2， i2=3， i3=4， i4=8， i5＝ 10， i6=11， i7=12， i8=13，满足： 7＜ 9＜ 16＜ 18 ＜ 19＜ 21＜ 22＜ 63，则存在长度为8的不下降序列。
问题为：当b1,b2,…， bn给出之后，求出最长的不下降序列。

这题也是很经典的一道题我们直接上解题步骤。
第一步：确定状态——原问题？子问题？
如果设F[i] 前i个数的最长不下降子序列——求不了啊~!为什么求不了？不知道这个序列的最后一个元素是哪个，没法转移。
所以我们设 F[i]以第i个数为结尾的最长不下降子序列。
第二步：确定状态转移方程
我们对于每个数a[i]，都找到它前面的不比它大的最长的序列连上去就能算出f[i]了，所以我们有：
f[i]=max{f[j]+1}（a[j]<=a[i] 且 j<i）
f[i] = 1
第三步：考虑是否需要优化
这里求max{f[j]+1}按照普通的写法是要O(n)，但其实我们可以写一棵权值线段树或者单调队列来维护，这样就能达到O(logn)的复杂度，感兴趣的同学可以自行学习一下。
第四步：确定实现方法
直接使用递推就好了。

递推版本代码如下：

for(i = 0; i < n; i++) {
    f[i] = 1;
    for(j = 0; j < i; j++) {
        if(a[j] <= a[i] && f[j] + 1 > f[i]) {
            f[i] = f[j] + 1;
        }
    }
}

记忆化搜索版本的代码如下：

int calc(int x) {
    if (f[x] != 0) return f[x];
    f[x] = 1;
    for (int i = 0; i < x; i++) {
        if (a[i] <= a[x]) {
            t = calc(i);
            if (t + 1 > f[x]) f[x] = t+ 1;
        }
    }
    return f[x];
}

滑雪

Michael喜欢滑雪，这并不奇怪， 因为滑雪的确很刺激。可是为了获得速度，滑的区域必须向下倾斜，而且当你滑到坡底，你不得不再次走上坡或者等待升降机来载你。 Michael想知道载一个区域中最长底滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子：
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一，当且仅当高度减小。在上面的例子中，一条可滑行的滑坡为24-17-16-1。当然25-24-23-...-3-2-1更长。事实上，这是最长的一条。

这道题我在大学的算法讲座中讲到过，是一道很有意思的动态规划题。我们直接上步骤：

第一步：确定状态——原问题？子问题？
原问题：从（1， 1）到（n， m）任意一个点滑下的最长路径长度
子问题： 从（i， j）滑下的最长路径长度
f[i][j]表示从（i， j）滑下的最长路径长度
第二步：确定状态转移方程 ——由于f[i][j]由上下左右四个方向转移过来
每个方向分开讨论能否划过来：
F[i][j] = max {f[i - 1][j] + 1 (a[i - 1][j]<a[i][j])
{f[i + 1][j] + 1 (a[i + 1][j] <a[i][j])
{f[i][j - 1] + 1 (a[i][j - 1] <a[i][j])
{f[i][j + 1] + 1 (a[i][j + 1] <a[i][j])
（初值）： f[i][j] = 1（至少经过自己一个点）
第三步：考虑是否需要优化
第四步：确定实现方法
这题递推是很不好写的，所以建议写记忆化搜索版本，大致框架如下：

int dfs(int x, int y) {
    if(f[x][y] > 0) return(f[x][y]);
    f[x][y] = max(分别递归四个方向中可以滑过来的);
    return(f[x][y]);
}

最大子串和

给你一个有正有负的序列，求一个子串（连续的一段），使其和最大！
样例输入： -5 6 -1 5 4 -7
样例输出： 14

这题也是很经典的一道题我们直接上解题步骤。
第一步：确定状态——原问题？子问题？
如果我们用f[i]前i个数的最大子串和——出现了和之前那题不下降子序列一样的问题：不知道f[i-1]中i-1选没
选所以f[i]没法求。所以我们用f[i]表示一定要选第i个数的情况下前i个数的最大子串和（选第i个数和其左边连续的若干个）
第二步：确定状态转移方程
由于每个数只有两种状态，自己开启一个新序列或者加入前面的序列。我们取一个最大值就好了：
• f[i] =max(f[i - 1]+a[i], a[i])
第三步：考虑是否需要优化
第四步：确定实现方法
这题直接使用递推就可以了。

最长公共子序列

给定两个序列X和Y， 当另一序列Z既是X的子序列又是Y的子序列时，称Z是序列X和Y的公共子序列。
最长公共子序列:公共子序列中长度最长的子序列。
给定两个序列X={x1,x2,…,xm}和Y={y1,y2,…, yn}， 找出X和Y的一个最长公共子序列。
样例输入： abcfbc
abfcab
样例输出： 4

这题也是很经典的一道题我们直接上解题步骤。
第一步：确定状态——原问题？子问题？
• f[i][j]表示前一个字符串的前i位与后一个字符串的前j位的最长公共子序列长度
第二步：确定状态转移方程
我们只需考虑表示前一个字符串的第i位与后一个字符串的第j位能否匹配就好了：
当x[i]==y[j]， f[i][j]=f[i-1][j-1]+1
当x[i]!=x[j]， f[i][j]=max(f[i - 1][j] ,f[i][j - 1])
a[1]==b[1] f[1][1] = 1
else f[1][1] = 0
第三步：考虑是否需要优化
第四步：确定实现方法
这题直接使用递推就可以了。

到这里我们的经典线性动态规划模型就讲的差不多啦。

结语

通过这篇BLOG，相信你已经对动态规划有一定理解并且掌握了线性动态规划啦。对于线性动态规划我的建议是在想不出解法的时候多去列列表找找数之间的关系，然后用我们的四步法依次求解，这样就能较快完成相关题目。最后希望你喜欢这篇BLOG！