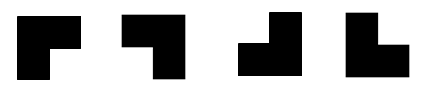看了中山纪念中学宋新波dalao在NOI2018雅礼冬令营的分治算法后，大受启发，参考了一下dalao的PPT，下面就来讲一下神奇的分治算法的四种经典应用。

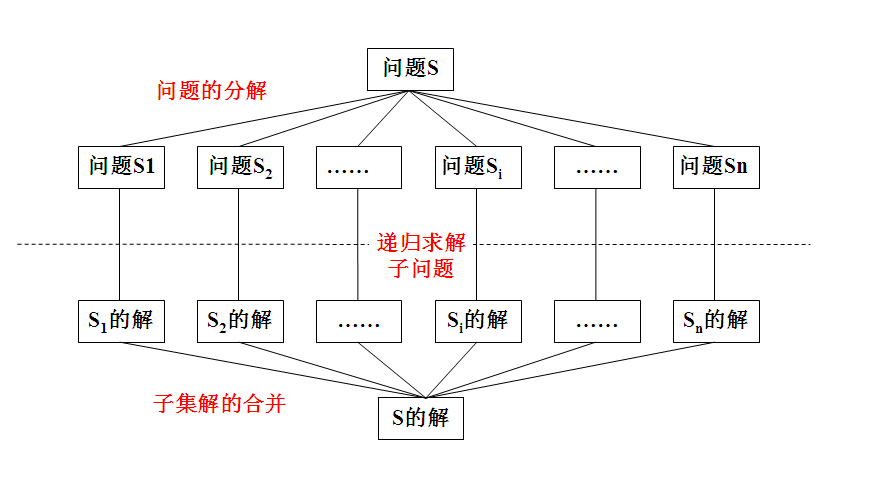
分治思想

分治(Divide-And-Conquer)就是“分而治之”的意思，其实质就是将原问题分成n个规模较小而结构与原问题相似的子问题；然后递归地解这些子问题，最后合并其结果就得到原问题的解。
其三个步骤如下：

①划分问题(Divide)：将原问题分成一系列子问题。
②递归解决(Conquer)：递归地解各子问题。若子问题足够小，则可直接求解。
③合并问题(Combine)：将子问题的结果合并成原问题的解。

如快速排序、归并排序等都是采用分治思想。

经典问题1—棋盘覆盖

有一个2k*2k的方格棋盘，恰有一个方格是黑色的，其他为白色。你的任务是用包含3个方格的L型牌覆盖所有白色方格。黑色方格不能被覆盖，且任意一个白色方格不能同时被两个或更多牌覆盖。如下图所示为L型牌的4种旋转方式。

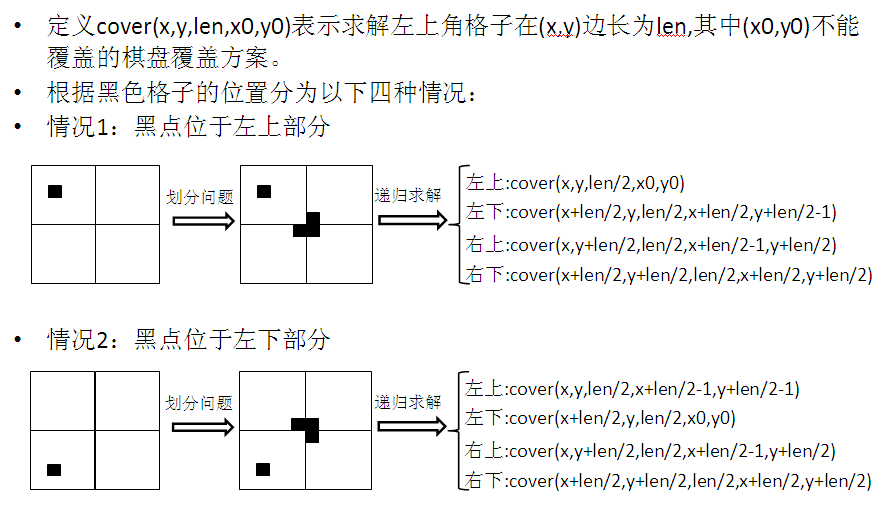
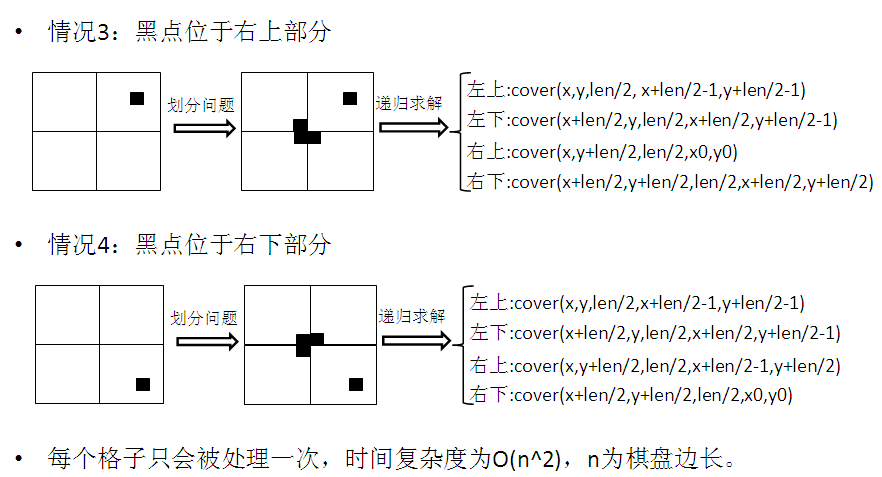
题目是要求用L型牌覆盖一个2^k*2^k的方格棋盘，棋盘有且只有一个黑色方格，且此方格不能被覆盖。

用分治来解决，把原棋盘平均分为4块，通过用1个L型牌覆盖棋盘正中间22的区域中的三个格子，把原棋盘分成4块2^k-12^k-1的方格棋盘,且每块中只含有一个黑色方格(不能覆盖的格子)。

此时把原问题分解成4个结构与原问题一样的子问题，棋盘的大小(边长)每次减半，最终会出现边长为1的情况，直接求解即可,如下图：

具体代码如下：

void cover(int x,int y,int len,int x0,int y0)
      {
           int t,len1;
         if (len==1)return;
         t=++tot;
         len1=len/2;
         if (x0<x+len1&&y0<y+len1)cover(x,y,len1,x0,y0);
           else{board[x+len1-1][y+len1-1]=t;cover(x,y,len1,x0+len1-1,y0+len1-1);}
         if (x0>=x+len1&&y0<y+len1)cover(x+len1,y,len1,x0,y0);
         else{board[x+len1][y+len1-1]=t;cover(x+len1,y,len1,x+len1,y+len1-1);}
         if (x0<x+len1&&y0>=y+len1)cover(x,y+len1,len1,x0,y0);
         else{board[x+len1-1][y+len1]=t;cover(x,y+len1,len,x+len1-1,y+len1);}
         if (x0>=x+len1&&y0>=y+len1)cover(x+len1,y+len1,len1,x0,y0);
         else{board[x+len1][y+len1]=t;cover(x+len1,y+len1,len1,x+len1,y+len1);}
      }

经典问题2—归并排序

给定一个长度为N的序列，对其进行排序。

归并排序思想：
1.划分问题：把长度为N的序列尽可能均分成左右两部分；
2.递归求解：对左右两部分分别进行归并排序；
3.合并问题：把左右两段排好序的序列合并出最终的有序序列。

好了，剩下的问题就是，怎么进行合并呢？很简单，若我们已经把一个序列的左右两个子序列已经从小到大分别从小到大排列好了，如下图：

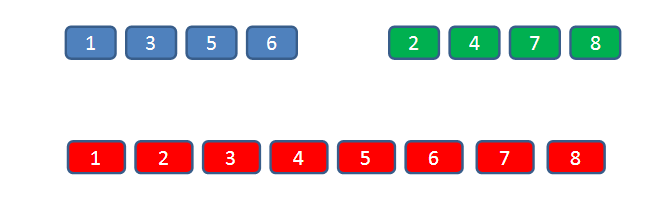
那么我们只需要定义两个指针i和j，开始时分别在两个子序列的开头，然后我们比较a【i】和a【j】的大小，若a【i】小于a【j】，那么就先输出a【i】，然后i后移一位；反之，若a【j】小于a【i】，那么就先输出a【j】，然后j后移一位，这样就可以得出最后排好序的序列了。
具体代码如下：

void merge(l,m,r)// 合并操作
     {
        // i 代表左半序列目前最小的位置
       // j 代表右半序列目前最小的位置
      // a：原数组b 数组：暂存数组（合并过程不能覆盖原数组）
      int i = l, j = m+1, k = l;
      for(; i<=m && j<=r; )
      if(a[i] <= a[j]) b[k++] = a[i++]; // 加入左边最小的
      else b[k++] = a[j++]; // 加入右边最小的
      // 加入剩余的数
      for(; i<=m; b[k++] = a[i++]); // 加入剩余左半的数
      for(; j<=r; b[k++] = a[j++]); // 加入剩余右半的数
      for(i=l; i<=r; i++) a[i] = b[i]; // 从暂存数组中赋值
    }

void merge_sort(int l, int r) // 排序位置从l 到r 的序列
     {
         if(l==r) return; // 长度为1 则不需要排序
         int m = (l+r) / 2; // 分成两段
         merge_sort(l, m); // 排序左半段
         merge_sort(m+1, r); // 排序右半段
         merge(l,m,r);//把两段排好序的序列合并成一个有序序列
    }

经典问题3—逆序对统计

给定一个长度为N 的序列，定义它的逆序对数为；
二元组(i,j)，满足i小于j 且A[i]大于A[j]。要求统计逆序对数。
例如：对于A=[3 2 5 1 4]，逆序对数为5：3>2, 3>1, 2>1,5>1, 5>4。

下面介绍一种使用归并排序计算逆序对的方法(利用分治算法的思想) 。

长度为N 的序列的逆序对数ans 可以分为3部分:
① 左半段的逆序对数L_ans
②右半段的逆序对数R_ans
③(i,j)分立两侧的逆序对数C_ans

• 结论：ans = L_ans + R_ans + C_ans

而且，ans = L_ans + R_ans + C_ans
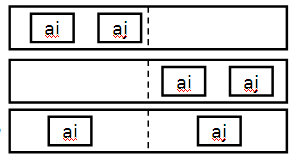
其中L_ans，R_ans是与计算ans相同类型的子问题，递归计算即可。主要考虑(i,j)分立两侧的逆序对数C_ans:
结论：对两半段的数分别排序， (i 在左半段，j 在右半段，排在不同位置不影响先后关系) ，C_ans 不变。

考虑(i,j)分立两侧的逆序对数C_ans:
考虑在合并过程中，统计它们的分立两侧逆序对总数：
左部分区间为[L,m],右部分[m+1,r]，在合并过程中，左右指针分别为i,j，当出现A[i]>A[j]时,(i,j)是一个逆序对，且A[L..m]是升序,所以(i+1,j),(i+2,j)…(m,j)也都是逆序对，答案ans可以直接增加m-i+1。

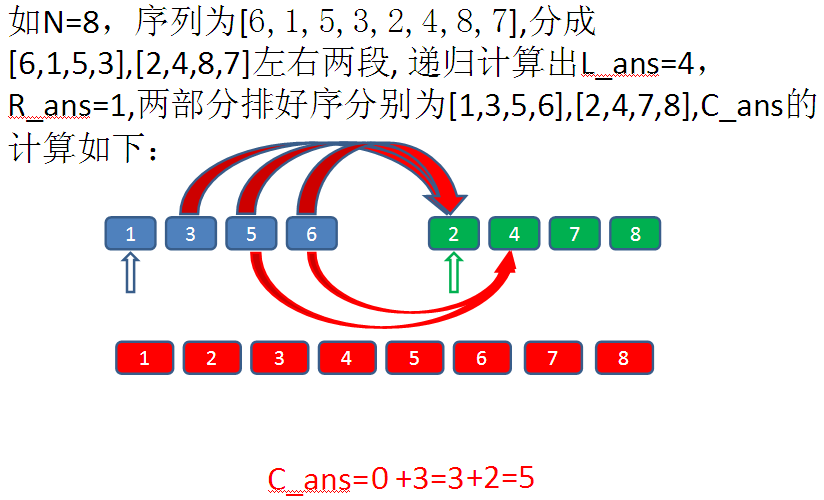
可以直接套用归并排序的模板，在合并过程顺便统计逆序对数。对于合并程序稍作改变：

void merge(l,m,r)// 合并操作,同时统计逆序对
     {
      int i = l, j = m+1, k = l;
      for(; i<=m && j<=r; )
      if(a[i] <= a[j]) b[k++] = a[i++]; // 加入左边最小的
      else ans += m-i+1,b[k++] = a[j++]; 
      // 插入右半段的时候，逆序对数增加
      for(; i<=m; b[k++] = a[i++]); // 加入剩余左半的数
      for(; j<=r; b[k++] = a[j++]); // 加入剩余右半的数
      for(i=l; i<=r; i++) a[i] = b[i]; // 从暂存数组中赋值
    }

经典问题4—最近点对问题

这个在之前的博客已经讲过了，详细点击这里！
这篇博客的第二部分很详细的讲解了这类问题的求法。

结语

非常实用（玄学）的分治，希望你喜欢这篇博客！