上篇博客我们重点讲解了tarjan算法的实现以及它最重要的用法——求解强连通分量。这篇博客我们就继续学习一下tarjan的其他经典用法。

运用tarjan求割点

什么是割点

在无向连通图中，如果将其中一个点以及所有连接该点的边去掉，图就不再连通，那么这个点就叫做割点（cut vertex / articulation point）

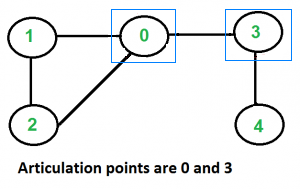
例如，在下图中，0、3是割点，因为将0和3中任意一个去掉之后，图就不再连通。如果去掉0，则图被分成1、2和3、4两个连通分量；如果去掉3，则图被分成0、1、2和4两个连通分量。

如何用tarjan求解

在上一篇关于tarjan的博客中我们说过，tarjan是基于DFS的。所以在tarjan过程中，我们会在图上DFS出一颗或几颗（如果图不连通）解答树。

我们仍以刚刚那幅图为例子：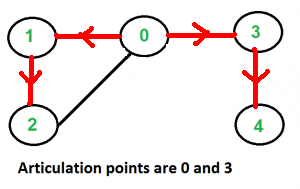
若以0为根节点，那么我们的DFS树就可能会如上图所示的红边一般。

然后我们很自然的根据tarjan算法，会求出每个点i的dfn[i]和low[i]，顺便再记录一下每个点在解答树上的儿子数量child[i]和每个节点的父亲fa【i】（若fa【i】==0，那么i就是根节点）。

然后我们分类讨论一下i，如果i是根节点,那么我们很明显的发现如果i有两个以上的儿子，则i为割点。（因为这棵树是DFS出来的，如果存在两个以上的子树，那么根节点就是这几个儿子互相到达的必经节点【若不是必经节点，那在之前的DFS中应该早就DFS出来了，不会成为根节点的另一个儿子！！！】）代码如下：

if(fa[x]==0 && child[x]>=2)bj[x]=1;

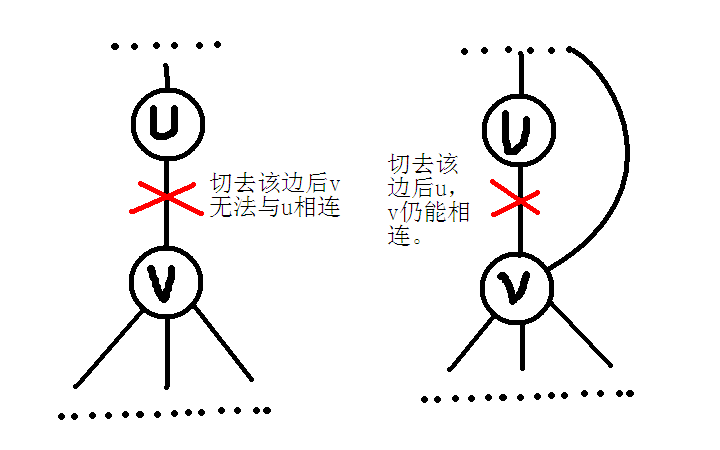
那么如果i不是根节点呢？首先如果i是叶子节点（i无儿子），那么i肯定不是割点。如果i不是叶子节点，且i有儿子j不能回到i的上面（即low[j] >= dfn[i]），那么i如果消失，那么他的那个儿子j所在的子树肯定也和i的父亲所在的子树不相连了，成了两个联通块如下图：

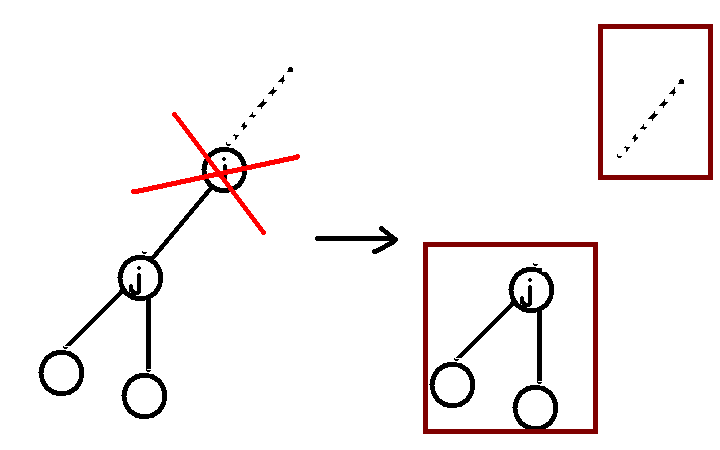
但如果j能够回到i的上面（即low[j] < dfn[i]）,那么i如果消失,j也依然和上面相连，如下图：

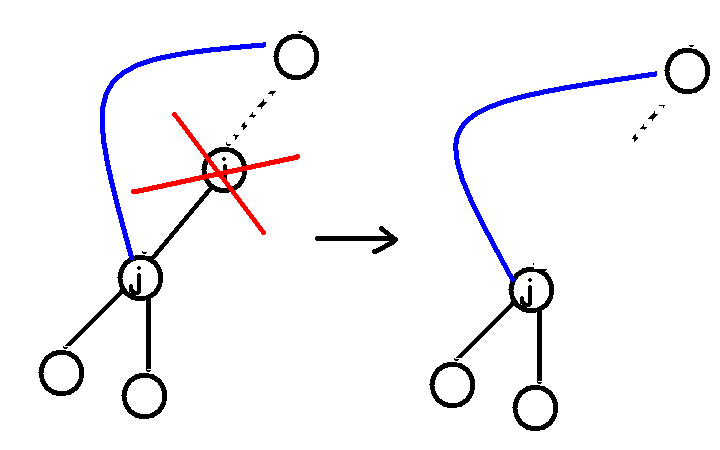
具体代码如下：

if(fa[x]>0 && low[y]>=dfn[x])bj[x]=1;

所以总的代码如下：

int tarjan(int x)
{
    tot++;dfn[x]=tot;low[x]=tot;
    stack[++indexx]=x;
    visit[x]=1;

    for(int k=last[x];k;k=a[k].next)
    {
        int y=a[k].y;
        if(dfn[y]==0)
        {
            fa[y]=x;child[x]++;
            tarjan(y);
            low[x]=my_min(low[x],low[y]);
            if(fa[x]==0 && child[x]>=2)bj[x]=1;
            if(fa[x]>0  && low[y]>=dfn[x])bj[x]=1;
        }
        else if(visit[y]==1)low[x]=my_min(low[x],dfn[y]);

    }

    if(dfn[x]==low[x])
    {
        do
        {  
            visit[stack[indexx]]=0;  
            indexx--;  
        }
        while(x!=stack[indexx+1]);

    }
    return 0;

}

一些需要注意的点

在之前的tarjan求强连通的算法中，我们在处理访问到已经访问过的点的操作是

if(visit[y]==1)low[x]=my_min(low[x],low[y]);

但这样的话就会WA掉，我们要改成

if(visit[y]==1)low[x]=my_min(low[x],dfn[y]);

这是因为关于tarjan算法，一直有一个很大的争议，就是low[u]=min(low[u],dfn[v]);

这句话，如果改成low[u]=min(low[u],low[v])就会wa掉，但是在求强连通分量时却没有问题

根据许多大佬的观点，在求强连通分量时，如果v已经在栈中，那么说明u，v一定在同一个强连通分量中，所以到最后low[u]=low[v]是必然的，提前更新也不会有问题，但是在求割点时，low的定义有了小小的变化，不再是最早能追溯到的祖先，（因为是个无向图）没有意义，应该是最早能绕到的割点，为什么用绕到，是因为是无向边，所以有另一条路可以走，如果把dfn[v]改掉就会上翻过头，可能翻进另一个环中，所以wa掉。需要特别注意。

运用tarjan求割边

什么是割边

割边：如果去掉某一条边之后，联通分量的数目变多，那么这个点就是割边；

换言之，就是如果对于一个连通图，去掉边(u,v)后，图就不连通了，那么这条边(u,v)就是我们要求解的割边了！

如何用tarjan求解

还是利用low[u]数组和dfn[u]数组来判断割边，对于任意一条边(u，v）【我们假定我们先发现u，即dfn【u】小于dfn[v]】：那么如果它是割边的话，就有low[v] > dfn[u] ,也就是以v为根的子树是封闭的，无法回到u点或u以上的点，只要去掉u,v连接的这条边，就会增加联通分量的数量，所以这条边(u，v）就是一条割边了。

程序部分

void tarjan ( int u , int p )    
{    
    dfn[u] = low[u] = ++times;    
    for ( int i = head[u] ; ~i ; i = e[i].next )    
    {    
        int v = e[i].v;    
        if ( !dfn[v] )    
        {    
            tarjan(v,u);    
            low[u] = min ( low[u] , low[v] );    
            if ( low[v] > dfn[u] && !e[i].tag )    
                ans.push_back ( e[i].id );    
        }    
        else if ( v != p )    
            low[u] = min ( low[u] , dfn[v] );    
    }    
}    

运用tarjan进行缩点

什么是缩点呢？就是把每个强连通分量都当成一个超级节点，然后再把这个强连通分量每个点的信息合并到这个超级节点上：比如连边啊，点权啊什么什么的，具体要按照题目来定。如下图：

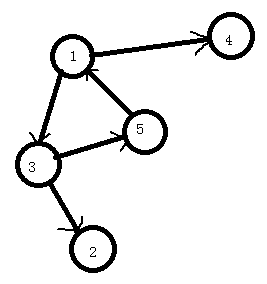
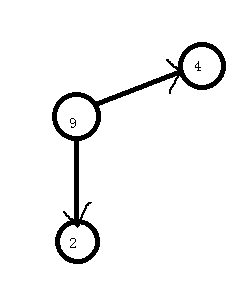
具体的代码只要在确定强连通分量后的那一段进行修改：
（color【i】=j表示第i个点属于第j个强连通分量【也就是超级节点里】）

if(dfn[x]==dfn[x])
    {
        tot++;//记录这是第几个强连通
        while(stack[indexx+1]!=x)
        {
            color[stack[indexx]]=tot;//修改所属强连通
            sum[tot]+=val[stack[indexx]];//点权合并 
            visit[stack[indexx--]]=0;
        }
    }

结语

那么到这里，tarjan就告一段落了，接下来如果我看到有其他经典的用法再来填坑吧！希望你喜欢这篇博客！