在之前的BLOG里,我们一起研究了两类无监督学习算法模型,在这一部分,就让我们一同来看看另一种无监督学习的模型——异常检测吧。
问题动机
在这篇BLOG中,我们将一同学习异常检测(Anomaly detection)算法,而这也是无监督学习机器学习算法的一个常见应用。这种算法的一个有趣之处在于它虽然主要用于非监督学习问题但从某些角度看又类似于一些监督学习问题。下面就让我们细细道来。
首先我们为什么要学习异常检测算法呢?为了解释这个问题让我我们从一个例子入手吧。假想我们是一个飞机引擎制造的检测员,当我们生产的飞机引擎从生产线上流出时,我们需要进行 QA (质量控制测试),而作为这个测试的一部分,我们测量了飞机引擎的一些特征变量比如引擎运转时产生的热量(x1)和引擎的振动(x2)。如果我们一共生产了 m 个引擎的话,若将这些数据绘制成图表看起来就应该是这个样子:
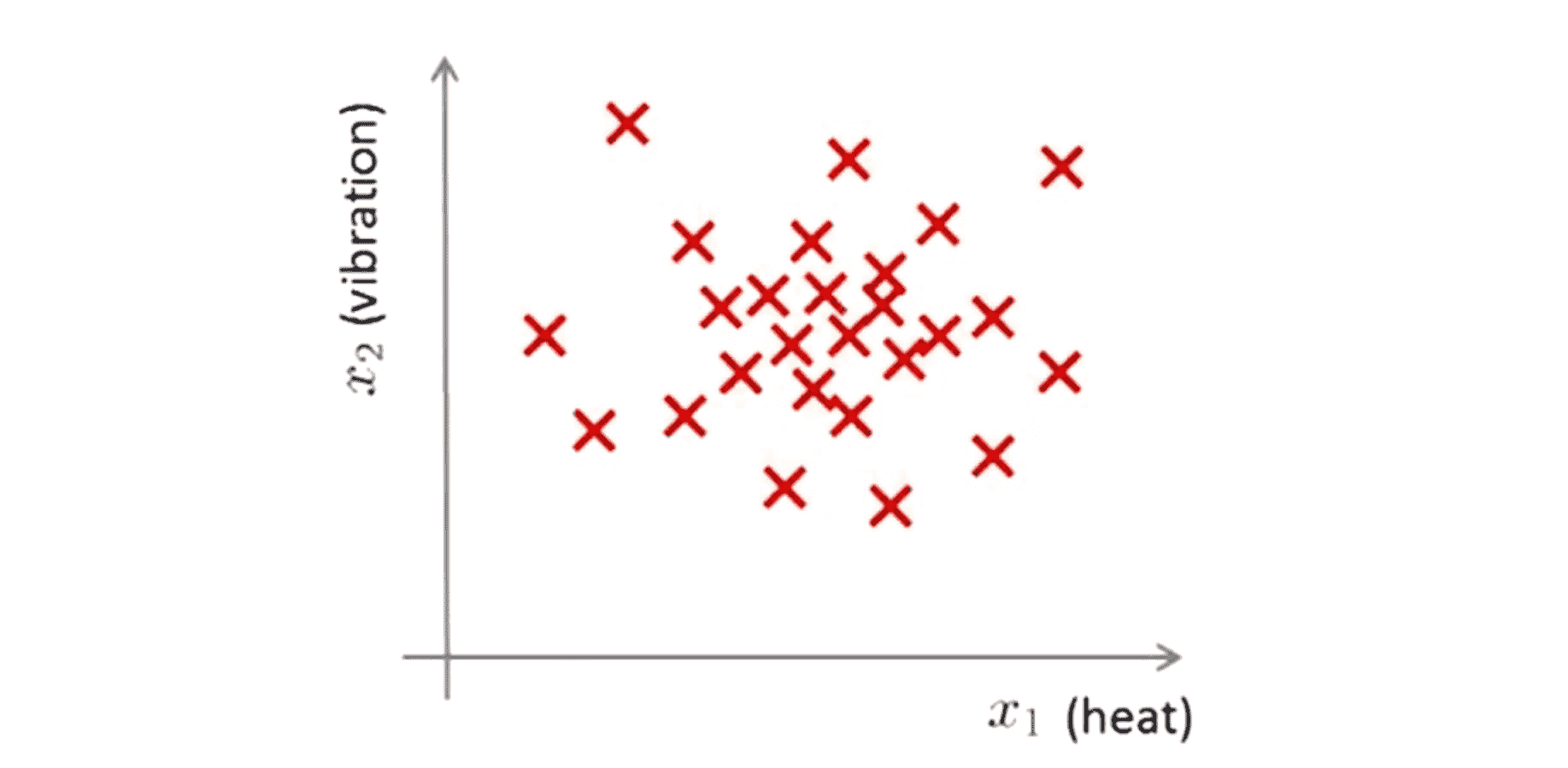
这里的任一个叉都是代表一个引擎的无标签数据。这样异常检测问题可以定义如下,我们假设后来有一天我们拿到一个新的从生产线上流出的飞机引擎其特征变量为x-test,所谓的异常检测问题就是我们希望知道这个新的飞机引擎是否有某种异常:
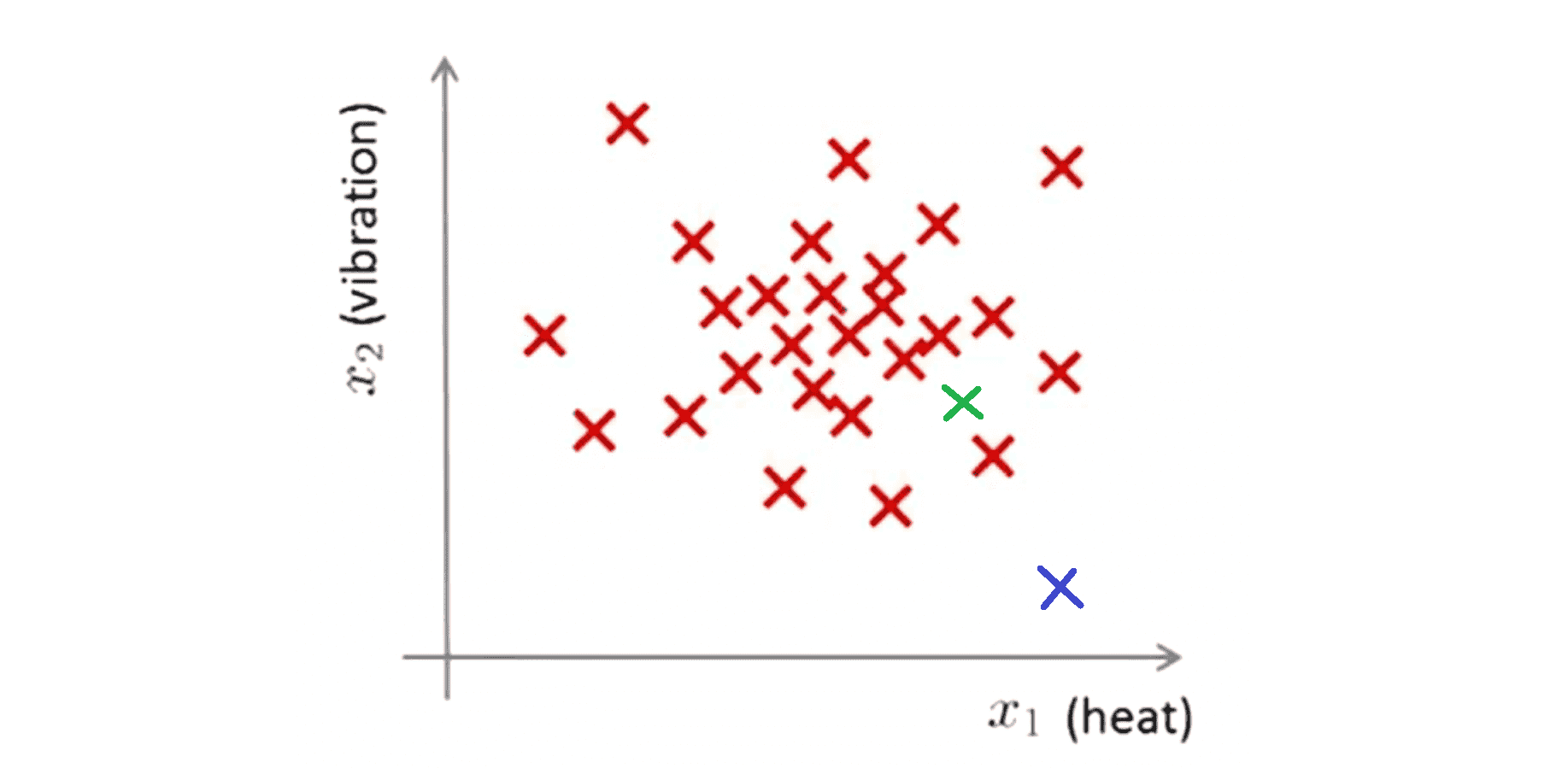
比如说 对于上图,如果我们的新引擎是绿色的叉,它看起来像我们之前见过的引擎,因此我们就可以认为它是正常的。然而如果我们的新飞机引擎是蓝色的叉,那么我们可以很自然地认为这是一个异常引擎,或许我们需要在向客户发货之前进一步检测这个引擎,因为它和我们之前见过的其他飞机引擎看起来不一样。
让我们来更正式的定义异常检测问题,如果我们有大小为 m 的代表正常数据的数据集x(1)……x(m),我们需要一个算法通过学习正常样本的特征来告诉我们对于一个新的样本数据 x-test 是否是异常,这就是异常检测问题。
那我们该如何设计这个算法呢?我们可以采取的方法是对于给定无标签的训练集,我们将对数据集建一个模型函数 p(x),也就是说我们将对 x 的分布概率建模。其中 x 是这些特征变量例如引擎运转时产生的热量(x1)和引擎的振动(x2)。当我们建立了 x 的概率模型之后,我们就会可以对于新的飞机引擎的特征也就是x-test,通过函数模型p(x)计算出p(x-test)后,如果p(x-test) < ε,即代表在我们根据训练数据得到的 p(x) 模型中x-test出现的可能概率非常低,所以我们就将其标记为异常。反之如果p(x-test) ≥ ε 我们就认为它是正常的。
因此在刚刚那个例子中,如果我们建立了一个模型,我们将很可能发现模型 p(x) 在中心区域的这些点有很大的概率被认为是正常的,而稍微远离中心区域的点概率会小一些,更远的地方的点它们的概率将更小,最外面的点就将成为异常点:
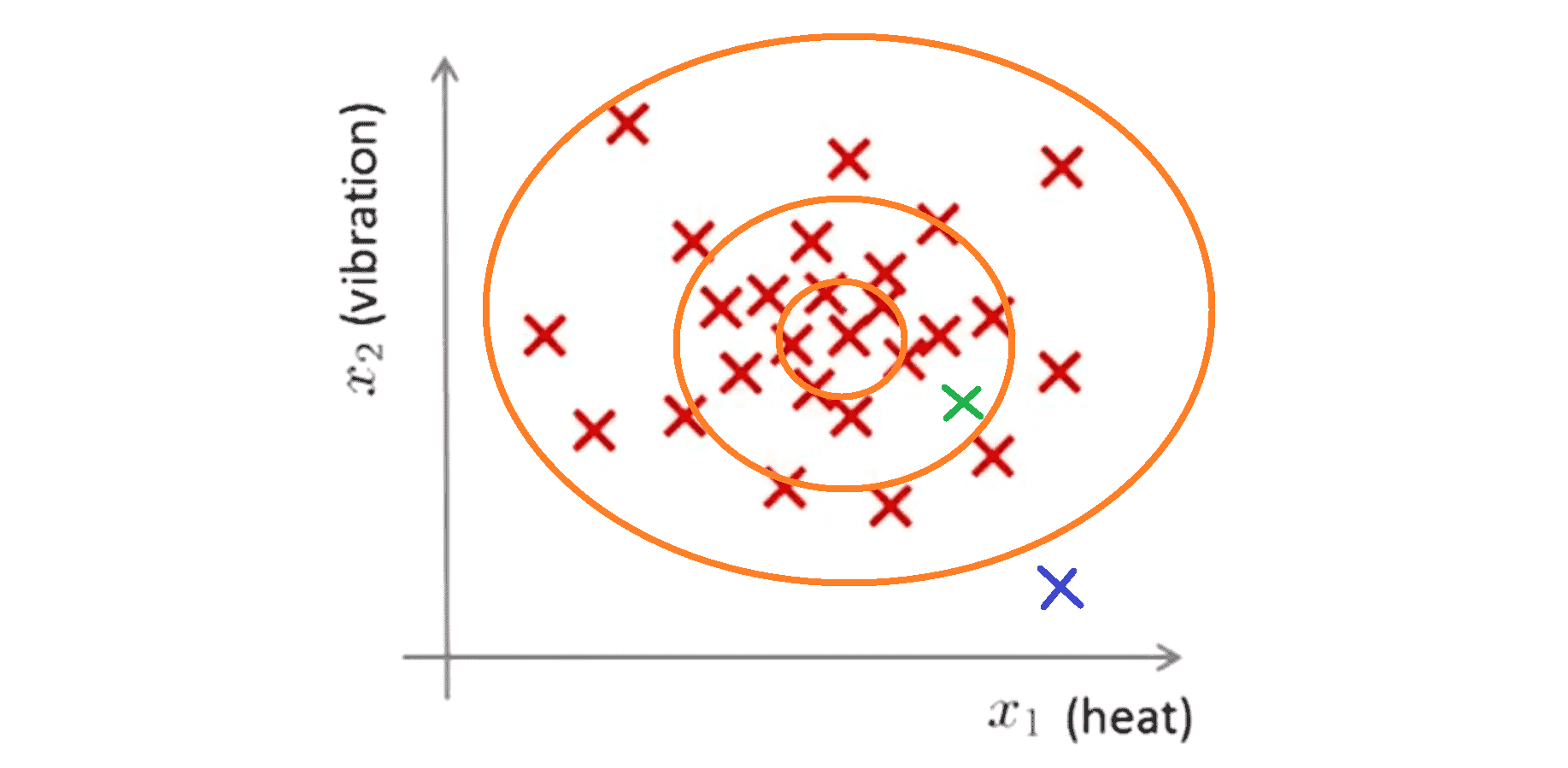
那异常检测只能拿来检测加工零件吗?当然不是,异常检测算法还有很多应用案例,其中最知名的要数欺诈检测。什么是欺诈检测呢?假设我们开了一个网站,有很多用户,我们就可以对不同的用户活动计算特征变量来建立一个模型,用来表示用户表现各种行为的可能性。比如假设 x1 是用户登陆的频率 ,x2 是用户的交易次数,x3 是用户在论坛上发贴的次数,x4 是用户的打字速度;接着我们就可以根据这些数据建一个模型 p(x) ,然后我们可以用它来发现网站上的一些行为奇怪的用户,比如打字速度异于常人的之类的。为了达到这个目的,我们只需要看哪些用户的p(x) < ε。 接下来我们就可以拿来这些用户的档案做进一步筛选或者要求这些奇怪的用户验证身份从而让你的网站防御异常行为或者欺诈行为。这样的技术将会找到行为不寻常的用户,其中不只是有欺诈行为的用户,也有被盗号的用户,还有滑稽行为的用户之类的。这就是许多在线购物网站常用来识别异常用户的技术。
异常检测的另一个例子数据中心的计算机监控,如果我们在管理一个计算机集群或者一个数据中心,其中有许多计算机,那么我们可以为每台计算机计算特征变量,也许某些特征是衡量计算机的内存消耗或者硬盘访问量或者CPU负载又或者一些更加复杂的特征。给定正常情况下数据中心中计算机的特征变量,我们就可以建立p(x)模型。接着如果我们发现有一个计算机它的正常概率 p(x) 非常小,那么我们就可以认为这个计算机运行不正常,或许我们应该将他停机维护。而目前这种技术实际上也正在被各大数据中心使用,用来监测大量计算机可能发生的异常。
好啦这就是异常检测算法的大致实现流程和实现动机,接下来让我们看看如何实现异常检测算法吧!。
高斯分布
在来推导异常检测算法前,让我们先来学习一个前置知识——高斯分布。什么是高斯分布呢?假设 x 是一个实数随机变量,如果x的概率分布服从高斯分布,那么我们一般记为x~N(μ, σ^2),其中数据的平均值为 μ,方差为 σ^2,如果我们将高斯分布的概率密度函数绘制出来,它看起来将是下面这样一个钟形的曲线:
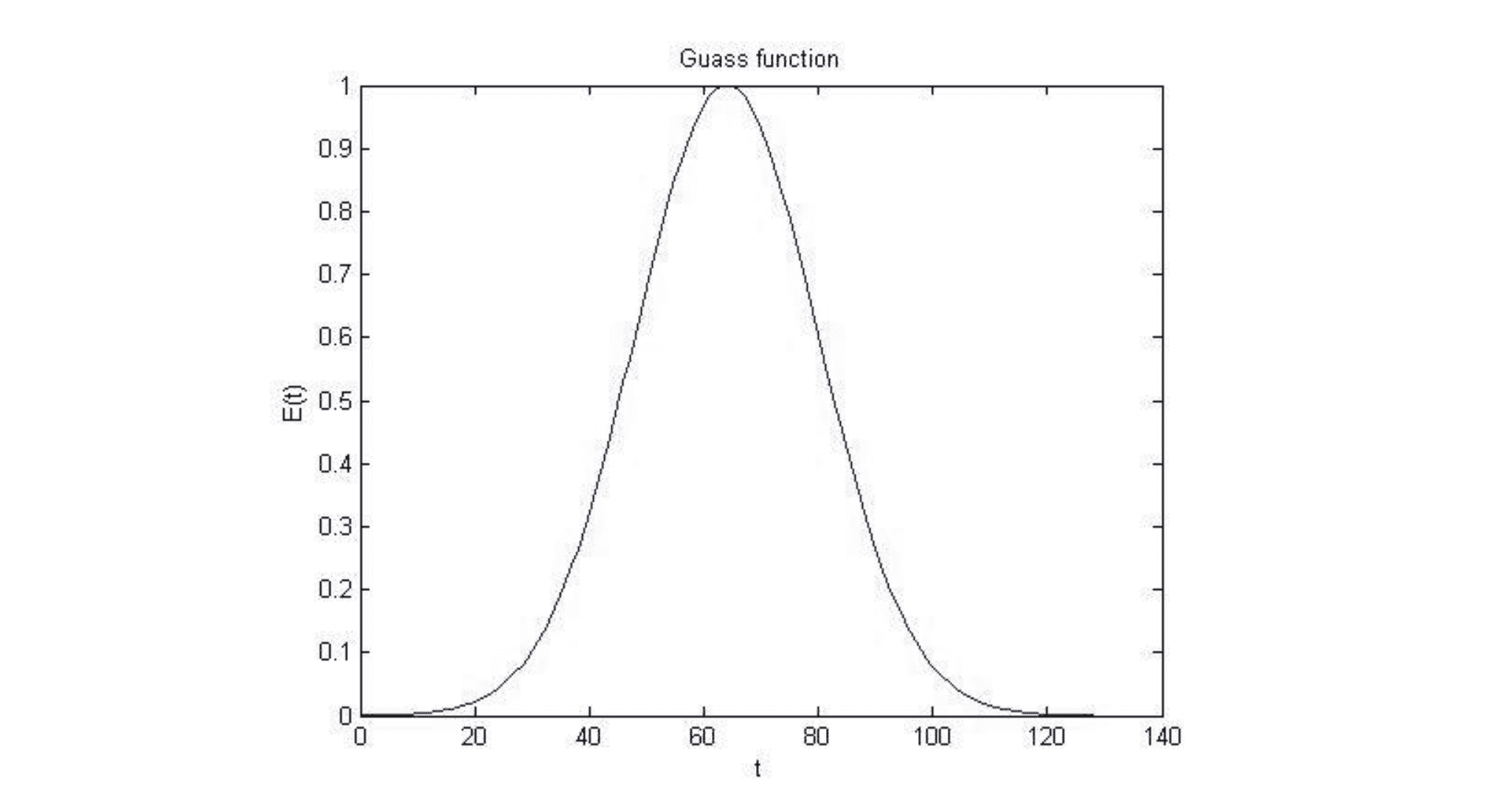
你在之前可能就见过这种钟形曲线,还记得高斯分布的两个参数 μ 和 σ 吗?体现在图像中,μ 控制的是这个钟形曲线的中心位置,而 σ 控制的是这个钟形曲线的宽度,因此参数 σ 有时也称作标准差。值得一提的是不管 μ 和 σ 取何值,曲线与 x 轴围城图像的面积都是 1 。这条钟形曲线决定了 x 取不同数值的概率密度分布,其具体计算公式是:
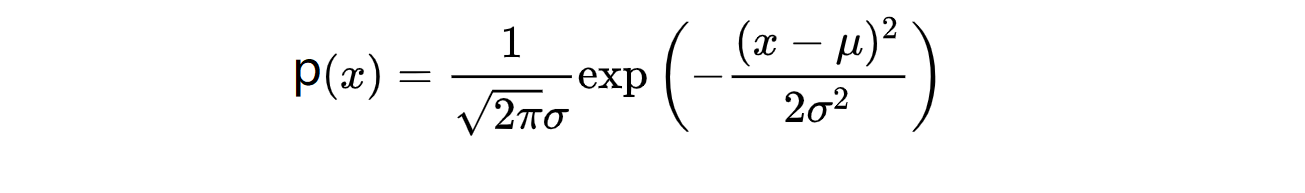
我们可以看到 x 取中心这些值的概率相当大,但在左右更远处数值的概率将逐渐降低直至消失。
也许上面的解说太过于硬核,没事让我们看几个高斯分布的图像来具体理解一下。如果 μ 取 0 ,σ 取 1,那么我们的高斯分布将以 0 为中心。这时因为 μ = 0 ,所以曲线的中心就在 x = 0,而图像宽度又由 σ 决定,故图像大致如下:
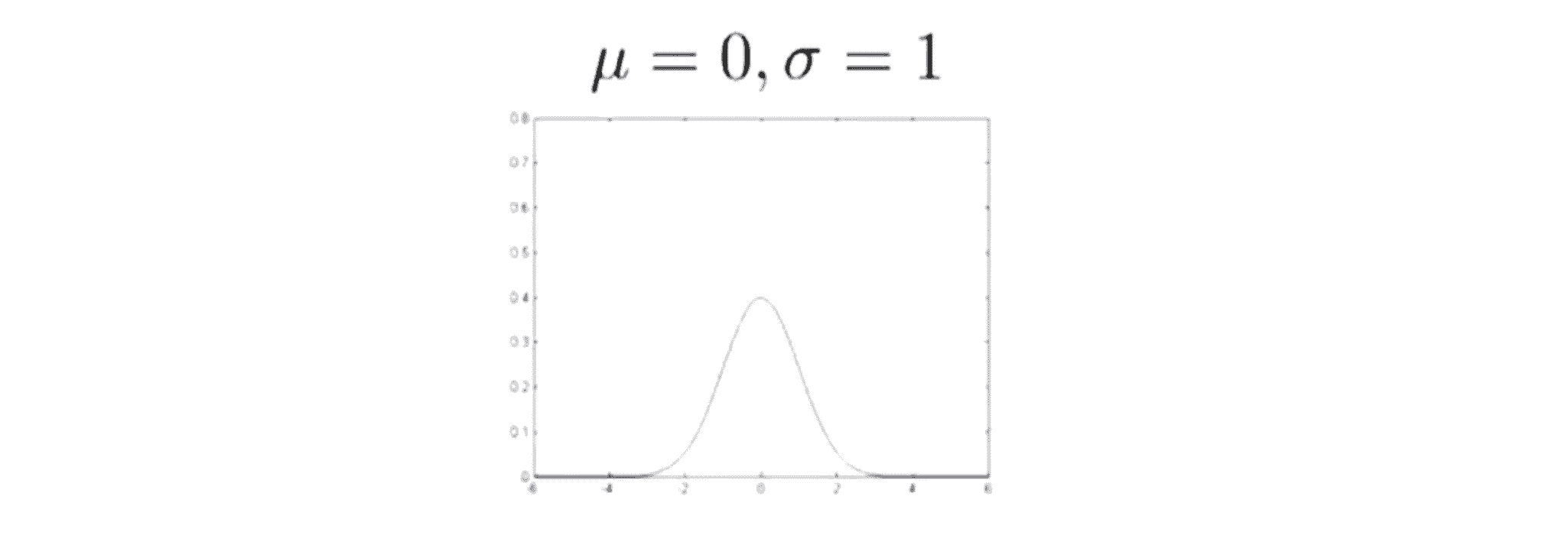
来看另一个例子,如果 μ 取 0, σ 取 0.5,这时候高斯分布的概率密度函数曲线会是下面这样的,仍然以 x = 0 为中心,但是现在它的宽度小了许多,因标准差变小了一半,导致高斯密度函数的宽度大约是之前的一半:
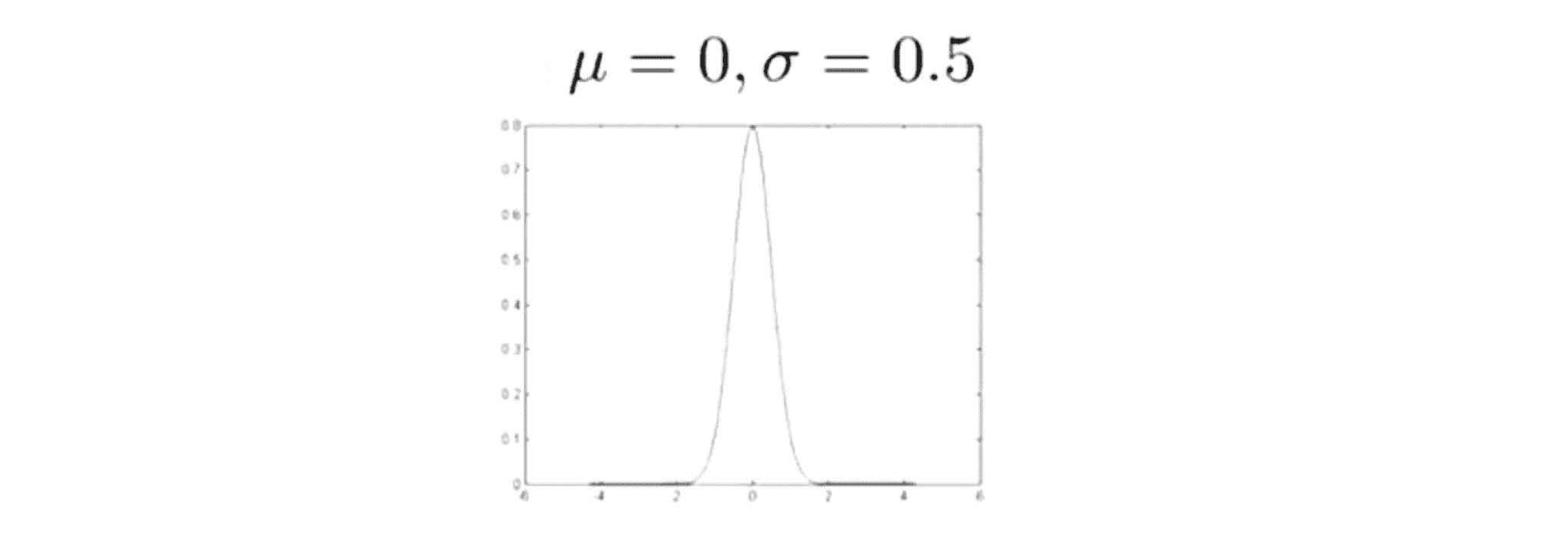
由于曲线下的面积是一定的,导致我们的图像也比原来高了一些。
再看一个例子,如果 μ 取 0, σ 取 2,那么我们将得到一个更胖更宽的高斯密度曲线:
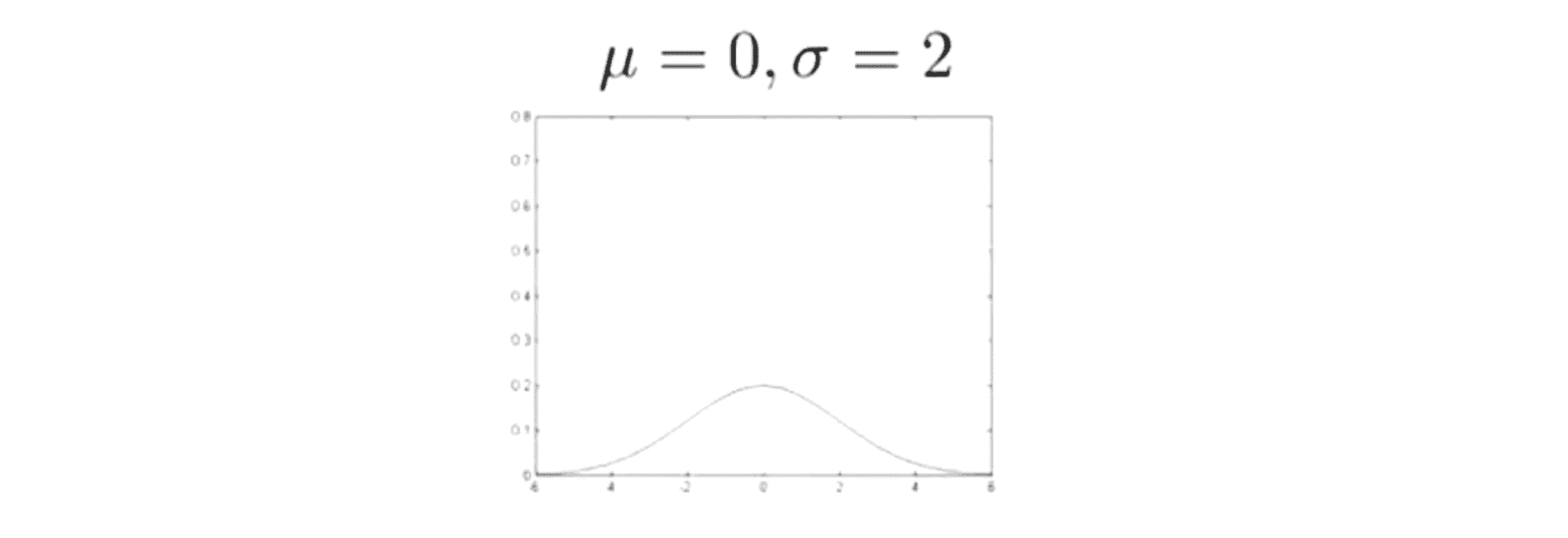
最后一个例子,如果我们也改变参数 μ ,那么曲线将不再以 x = 0 为中心,比如当 μ 取 3 的时候,曲线就以 x = 3 为中心,相当于整个高斯分布被平移了:
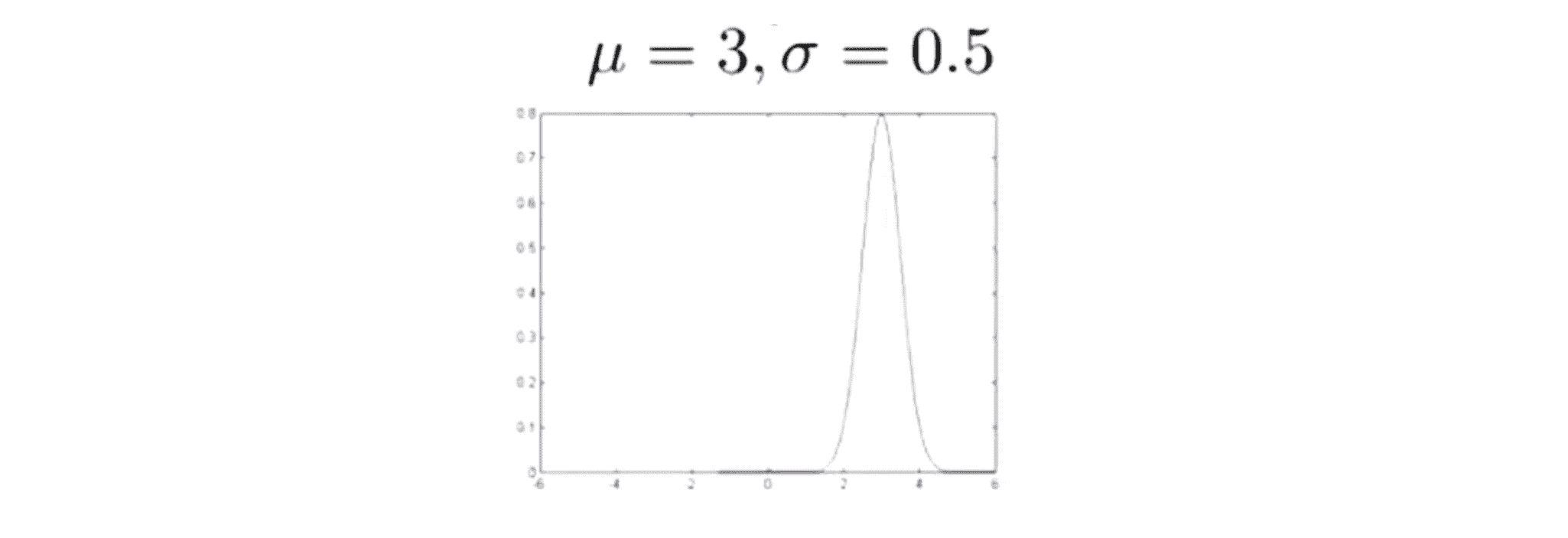
接下来让我们来看参数估计问题。什么是参数估计问题?假设我们有一个数据集其中有 m 个样本 x(1) …… x(m),比如下图:
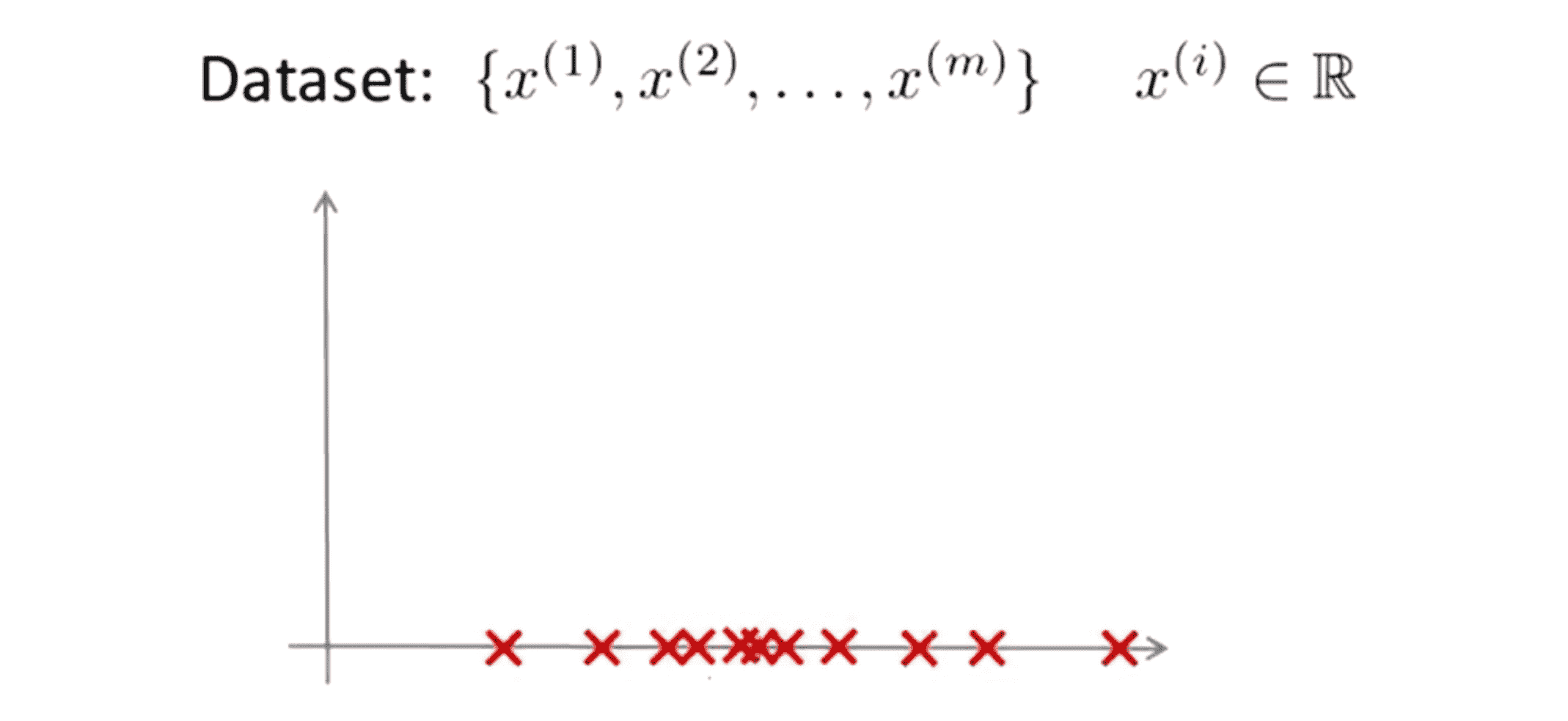
参数估计问题就是假设我猜测这些样本来自一个高斯分布的总体,我们如何估算出 μ 和 σ^2 的值:
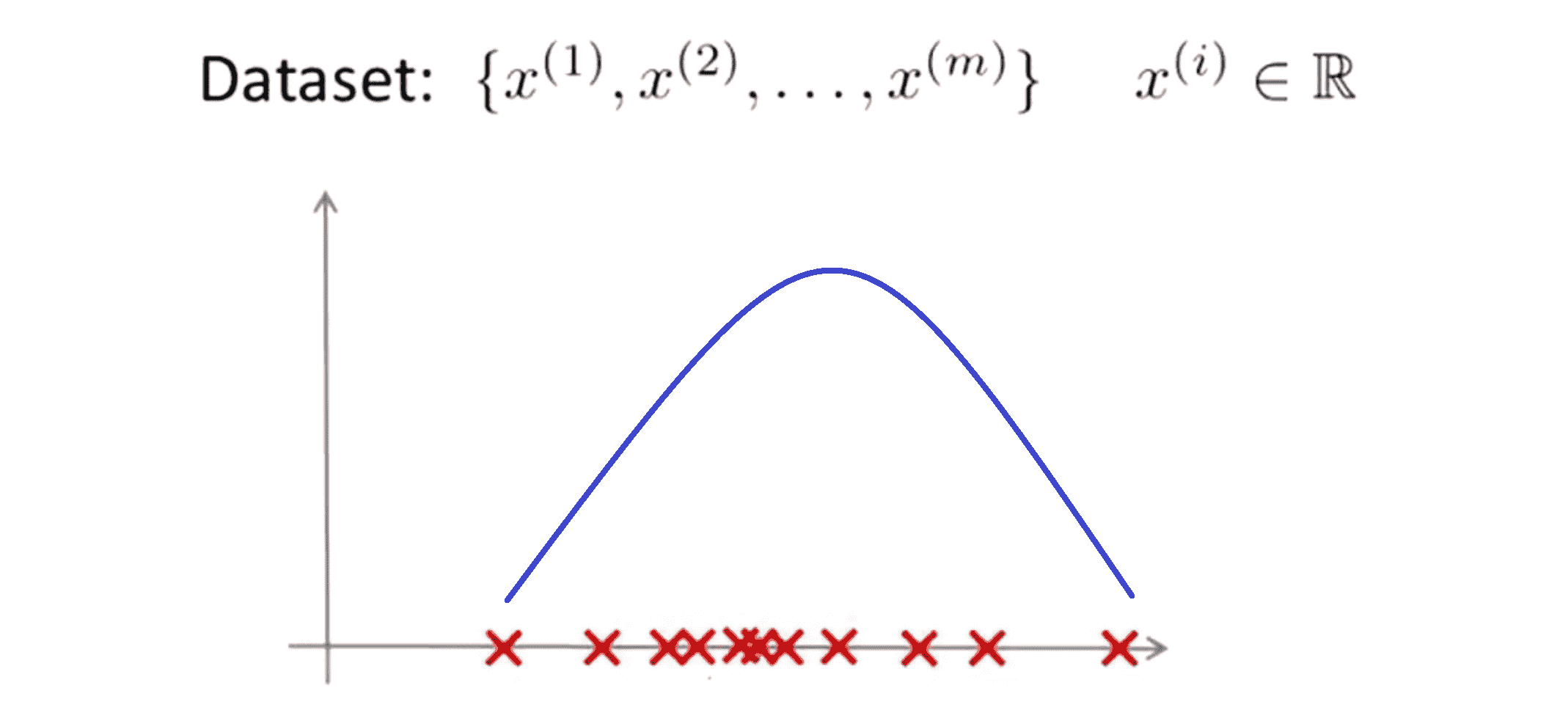
我们估计 μ 的方法是对我们的所有样本求平均值,μ 就是平均值参数而 σ^2 表示方差,故计算公式如下:
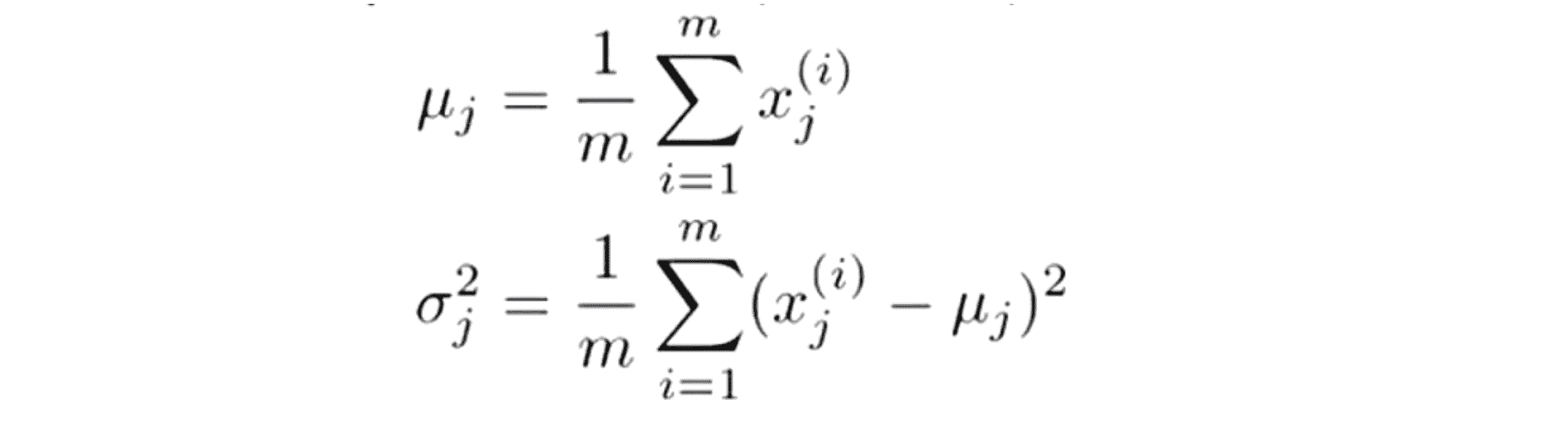
这里顺便提一下,你们有些人可能精通统计学,如果你是统计方面的专家应该听说过极大似然估计,而这里的估 实际就是对 μ 和 σ^2 的极大似然估计。最后再提一句,同样是针对那些学习过统计课程的人,如果你以前上过统计课程 你们可能会见过这么一个公式,在求方差的时候,乘以的不是 1/m 而是 1/(m - 1),其实在实际使用中到底是选择使用 1/m 还是 1/(m - 1) 其实区别很小,只要我们有一个还算大的训练集就基本察觉不出来。但是在机器学习领域大部分人更习惯使用 1/m 这个版本的公式。
在这一部分,相信你已经充分了解了高斯分布的细节。下一部分,我们将利用这些知识推导出异常检测算法的具体实现。
算法实现
在这一部分,我们将应用高斯分布开发异常检测算法。假如说我们有一个无标签的训练集,共有 m 个训练样本并且这里的训练集里的每一个样本都是 n 维的特征,因此我们的训练集应该是 m 个 n 维的特征构成的样本矩阵。现在我们解决异常检测的方法是从数据中建立一个 p(x) 概率模型来尝试计算出这些哪些特征出现的概率比较高,哪些特征的概率较低。很显然对于每一个样本,他的特征都可以写成向量 x ,x包含m个元素x1……xm。很显然对于不同的特征我们要分别计算出现概率,所以我们的概率应该写成p(x) = p(x1) p(x2) …… p(xm)。接着我们要做的是假定特征 x1 ……xm都服从高斯正态分布,那我们的式子就可以写成:

这就是我们要说的模型。顺便说一下对那些擅长统计的同学来说,实际上我们刚刚写的式子就对应于一个从 x1 到 xn 上的独立的假设。但实际中结果是无论这些特征是否独立这些算法的效果都还不错 。让我把这些式子写得紧凑点并带入之前正态分布下p(x)的计算公式我们就得到了上图中的第二行。
顺便再说一下估计 p(x) 的分布问题通常也被称为密度估计问题,下面我们的来看看异常检测算法的具体步骤。
第一步便是选择特征,我们可以尝试找出能看出数据集中存在异常的一些特征,比如引擎运转时产生的热量和引擎的振动。但更为普遍的是我们取尽可能尝试选择所有能够描述数据相关的属性的特征就可以了。
第二步时给出一组 m 个无标签数据构成的训练集x(1) …… x(m),我们对于特征x1……xn分别拟合出期望 μ1 …… μn 以及方差值 (σ1)^2 …… (σn)^2 ,这里同样可以使用向量化进行优化。
第三步,当给出一个新样本时比如当有一个新的飞机引擎时,我们想要知道这个飞机引擎是否出现异常要做的就是 计算出 p(x) 的值来,我们知道 p(x) 的值等于这个下面乘积式:

然后看看如果这个概率值很小,那么我们就将这一项标注为异常。
下面我们结合具体例子来说明吧。假如说我们有一系列数据,然后我们发现对于特征 x1 如其均值是5,标准差为2;然后你再来看第二个特征其平均值是 3 且其标准差值为 1,所以 σ1^2 = 4,σ1^2 = 1。如果绘制 p(x) 的图像也就是 这两个特征值分布概率值的乘积:
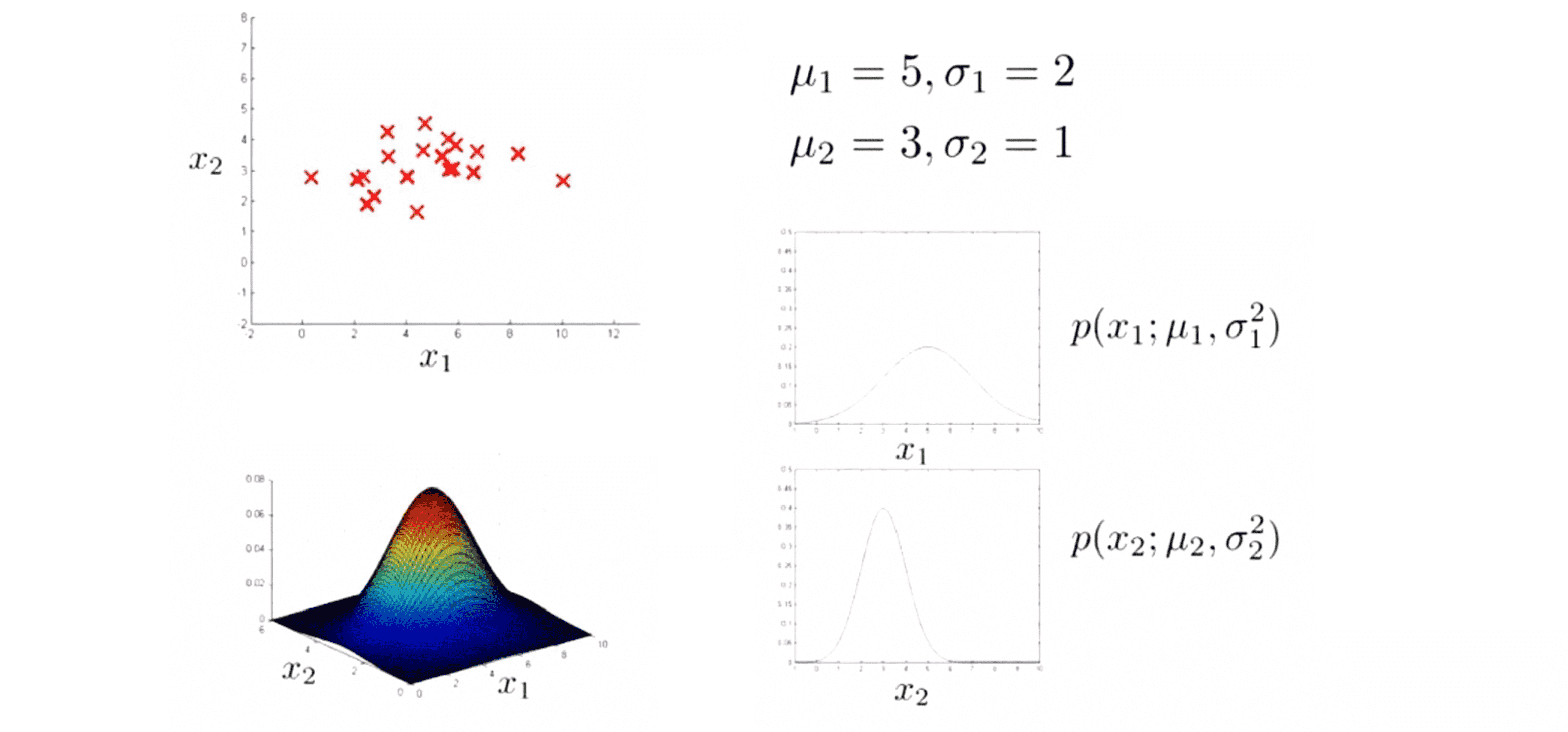
事实上我们会得到上图这样的立体图像,这就是 p(x) 值的图像。其中具体的某一点对应的高度值就表示 p(x) 值。其中 p(x) = p(x1; μ1,σ1^2) * p(x2; μ2,σ2^2)。 现在 我们就知道了如何从数据拟合参数,让我们看看一些新的样本。假如在这里我们有了一个新样本,我要知道这个样本是否异常:
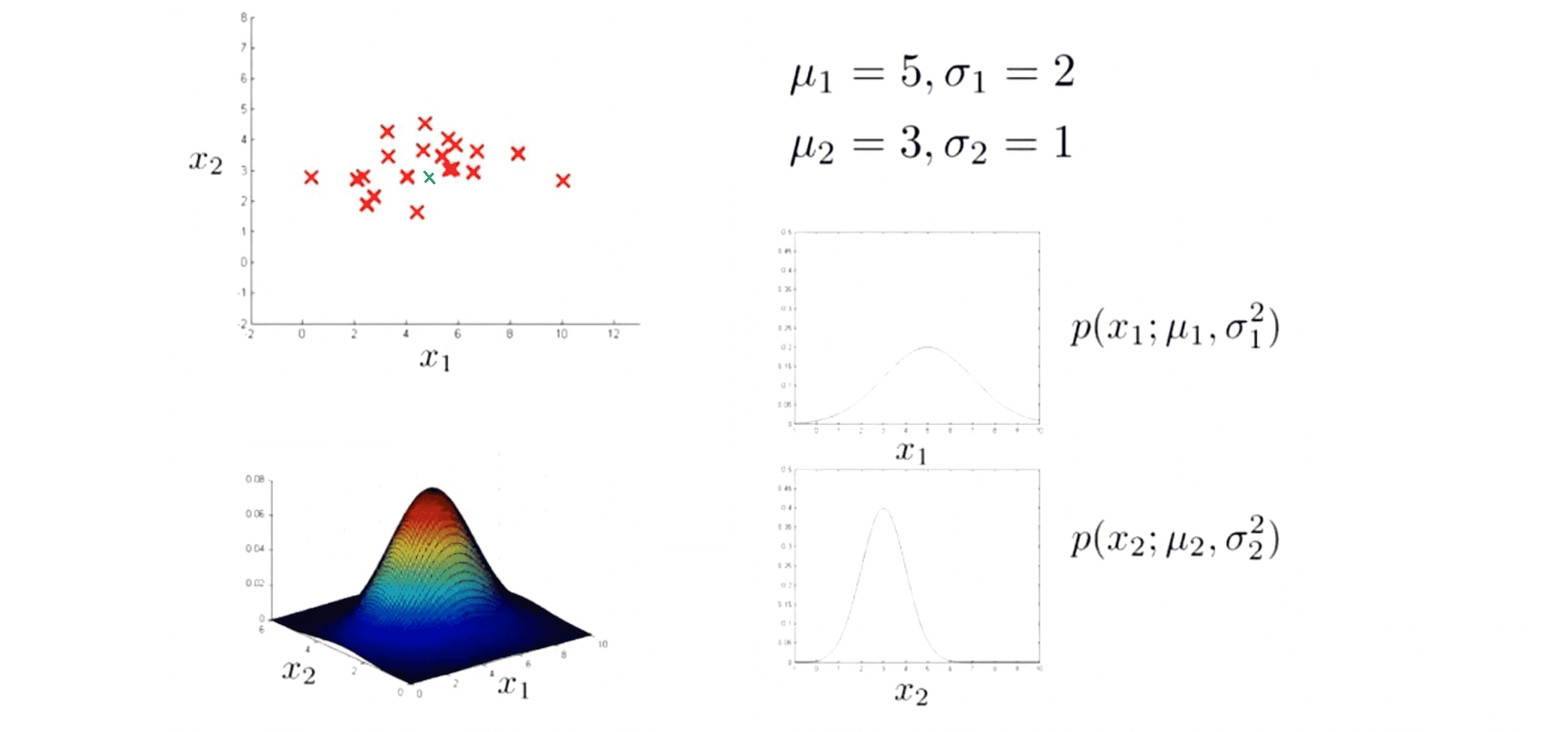
要回答这个问题,我们可以先给计算机设某个无穷小量ε的数值,假如我设置的 无穷小量ε数值为0.02,那么对于绿色的样本,我们称其为 x(1)test,不难发现这是一个相当大的数,具体地 这个值计算得到是0.0043,是大于等于 ε 值的,也就是代表这是一个正常的样本。
同时对于另一个蓝色的测试样本我们称其为 x(2)test:
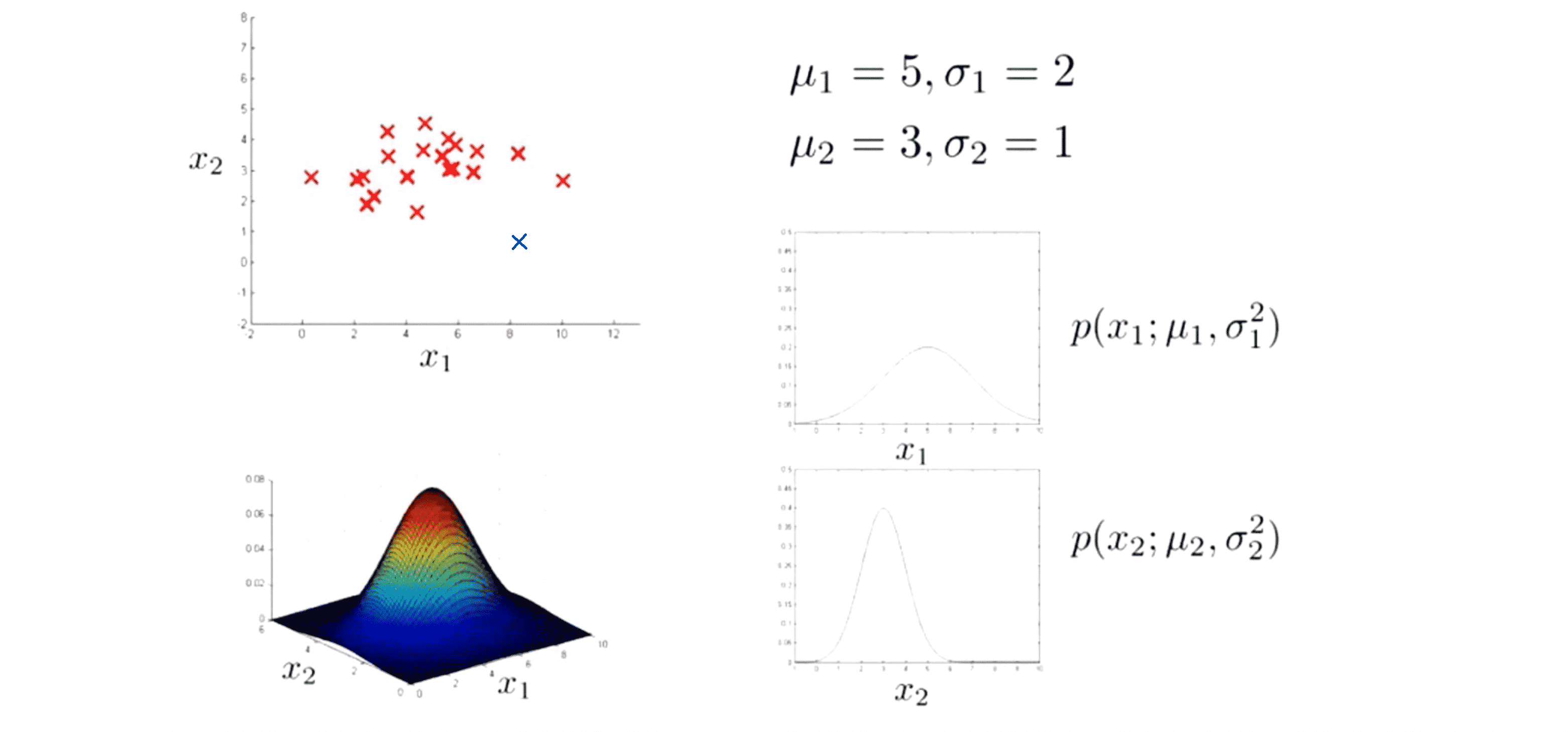
我们现在要做的是计算 p(x(2)test) ,接着我们发现p(x(2)test)=0.002,是一个比 ε 还要小很多的数,那么我们会说 x2 确实是一个异常数值。
除了这个方法外,我们也可以对这个方法进行改进。看这个三维表面图从图上不难发现在这个图的中间部分的 x1 x2 通常都对应于一个比较高的p(x)值,预示着非异常样本;而在周围边缘的点对应的概率值都是非常小的,因此我们会标记这些点为异常样本区域。所以我们也许可以定义某个区域,如下图中橙色线为分割线。在这个分割线里面的可以标记为非异常区表示无异常的样本,而外面的就是异常区域:
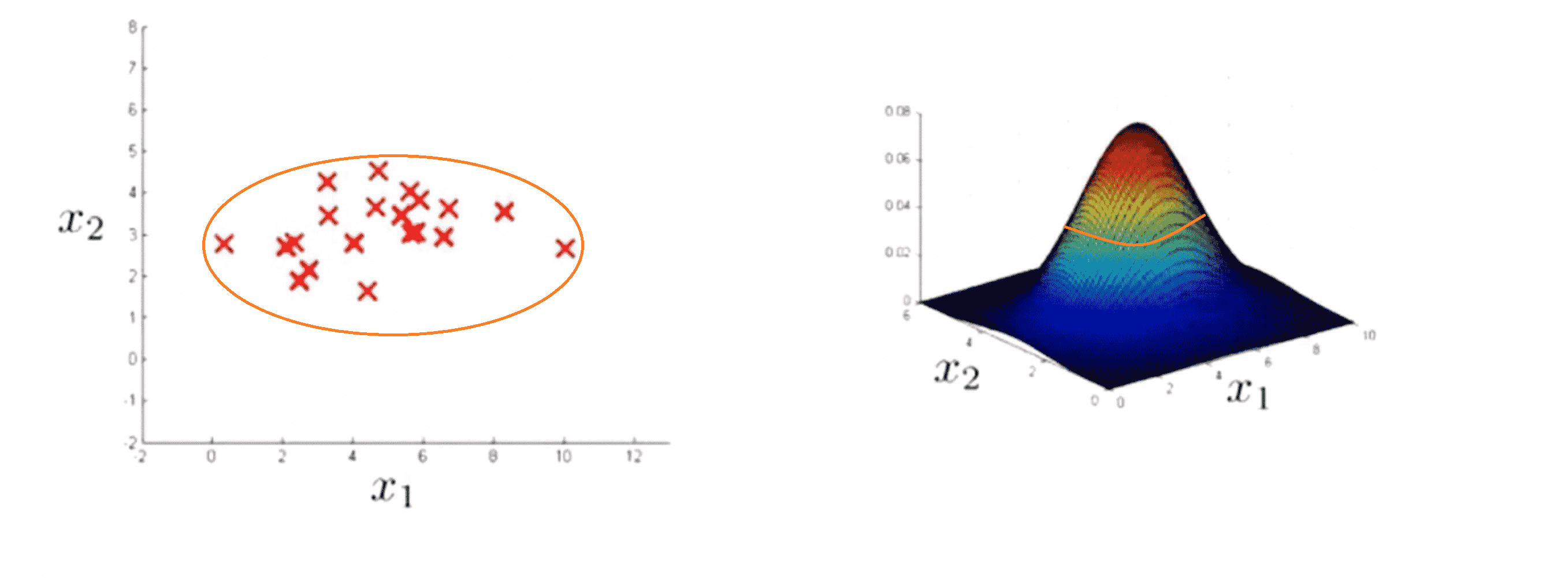
是不是有非监督学习内味了?关于异常检测算法和非监督学习的关系,我们在之后的BLOG也会重点提及。
结语
通过这篇BLOG,我们一同学习了如何拟合 p(x) 也就是 x 的概率值以共同开发出了一种异常检测算法。同时我们也学会了如何通过给出的数据集拟合参数进行参数估计得到参数 μ 和 σ 并检测新的样本是否是异常。在接下来的BLOG中,我们将继续深入研究这一算法同时更深入地学习怎样让算法工作地更加有效。最后希望你喜欢这篇BLOG!