对于降维问题来说,目前最流行且最常用的算法是主成分分析法 (Principal Componet Analysis, PCA),这篇BLOG就让我们手把手学习并实现PCA算法吧。
了解PCA算法
在这一部分,我想首先开始讨论 PCA 问题的公式描述。也就是说我们尝试用公式准确地精确地描述我们想让 PCA 来做什么。
假设我们有下图这样的一个数据集,这个数据集含有二维实数空间内的样本 X:
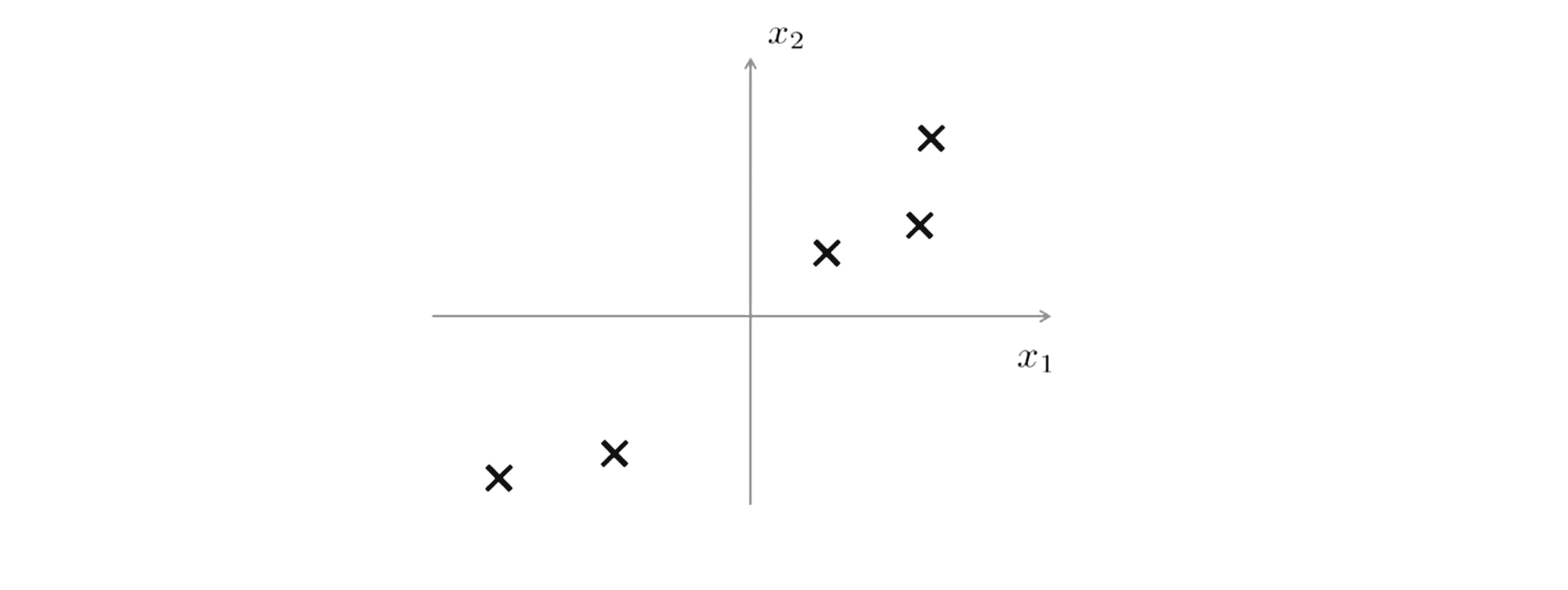
假设我们想对数据进行降维,像将其从二维降到一维。也就是说我们想找到 一条直线将数据投影到这条直线上。那怎么找到一条好的直线来投影这些数据呢?下图这样的一条直线也许是个不错的选择:
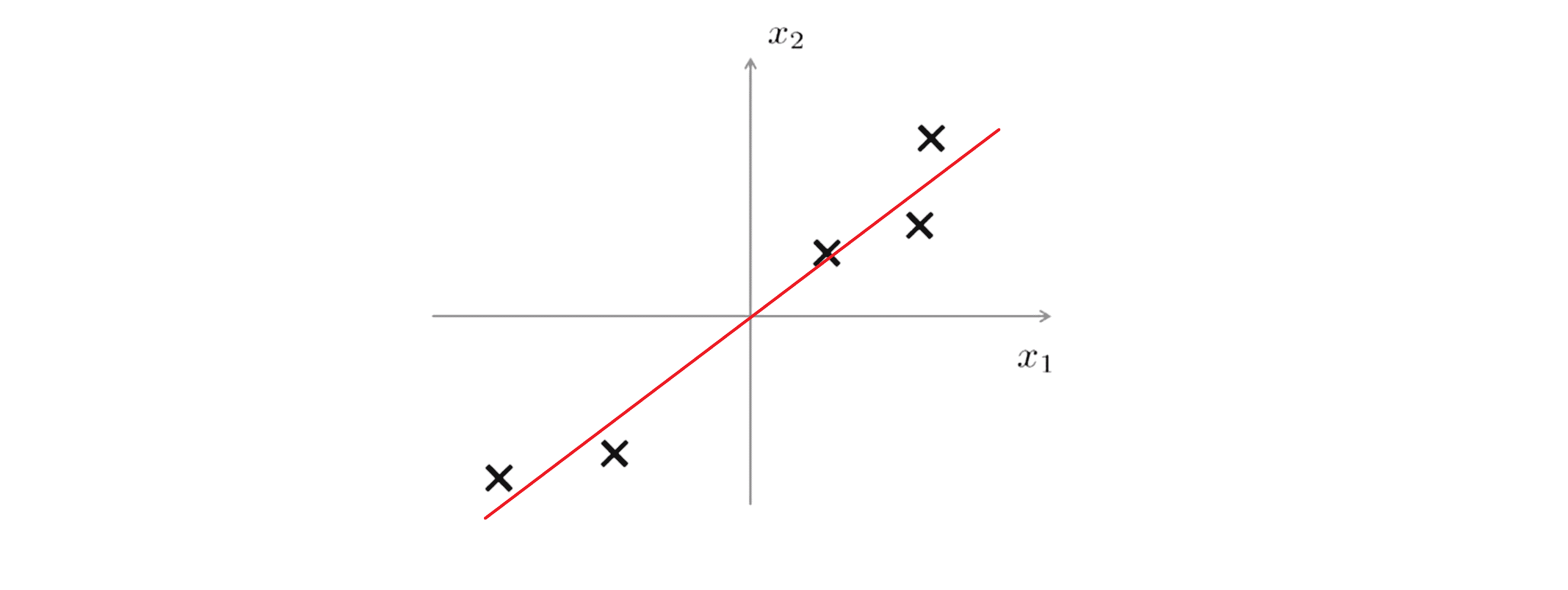
我们认为这是一个不错的选择的原因是每个点到它们对应的 投影到直线上的点之间的距离非常小,也就是说这些蓝色的 线段的长度总和非常的短,这些蓝色的线段也叫做投影误差:

所以其实正式的说 PCA 所做的就是寻找一个低维的面,我们将数据投射在低维的面上,使得这些蓝色小线段的平方和 达到最小值,即每个点到其投影点的距离的平方的累加和要最小。这就是我们PCA要做的事情。
回到这个例子,对比我们刚刚画好的红线,另一条对数据进行投影的粉红色直线看起来是一个非常糟糕的方向:
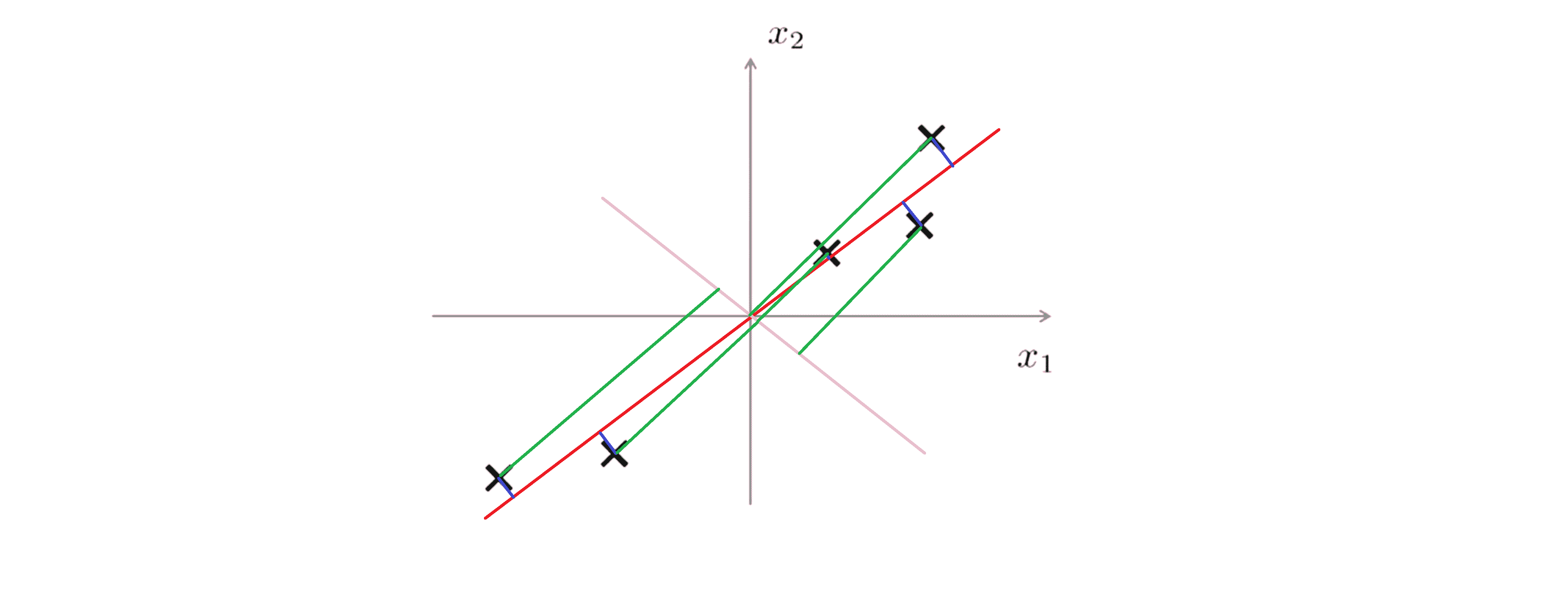
因为如果我将数据投影到这条粉红色的直线上,那么投影误差,就是这些绿色的线段将会很大,所以这些点将会移动很长一段距离才能投影到这条′红色直线上。根据我们之前分析的PCA的做法,我们知道主成分分析法会选择红色的这条直线而不是粉红色的那条。
另外在应用PCA之前,我们通常要先进行均值归一化和特征规范化,使得特征发均值为 0 且数值在可比较的范围之内。让我们正式一点地写出 PCA 问题的目标,如果我们对于下面这个数据集:
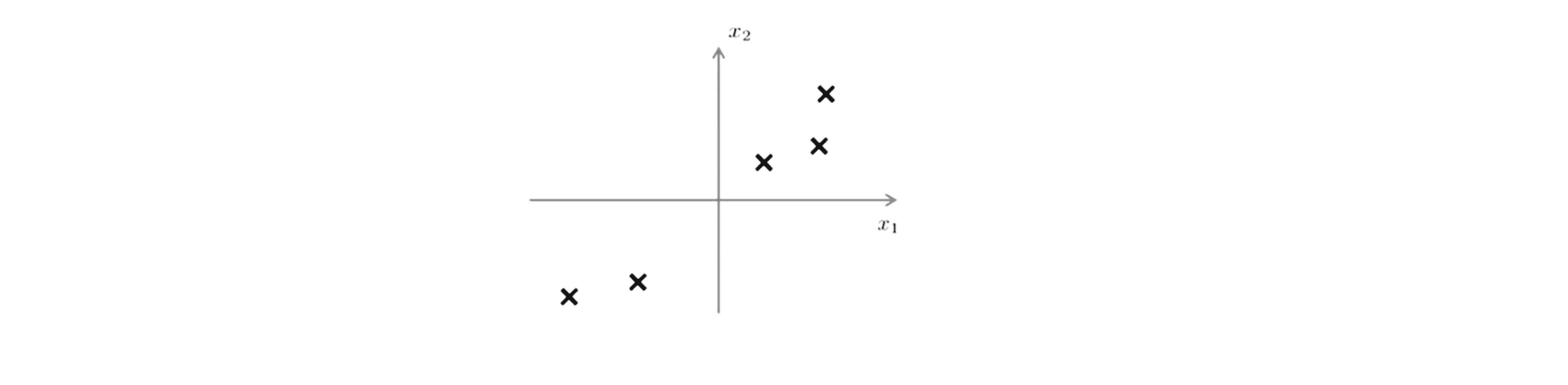
我们想将数据从二维降到一维的话,我们将试着寻找一个向量 u(i) 属于 n 维空间中的向量,即我们将寻找一个对数据进行投影的方向,使得投影误差能够最小。在这个例子里我们希望 PCA 寻找到下图这样的一个向量 u(1):
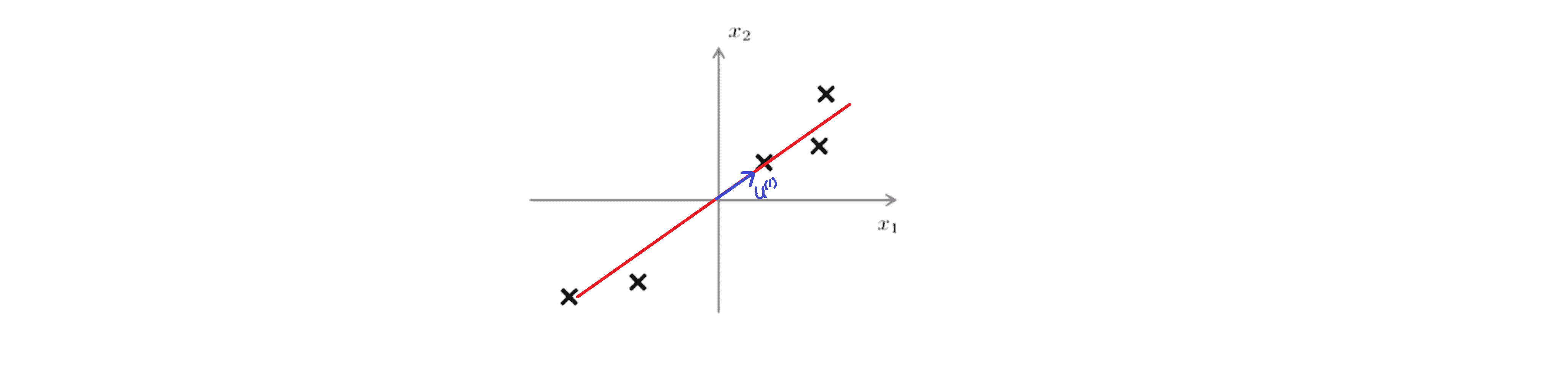
当我们把数据投影到这条直线上时,其投影误差能够最小:
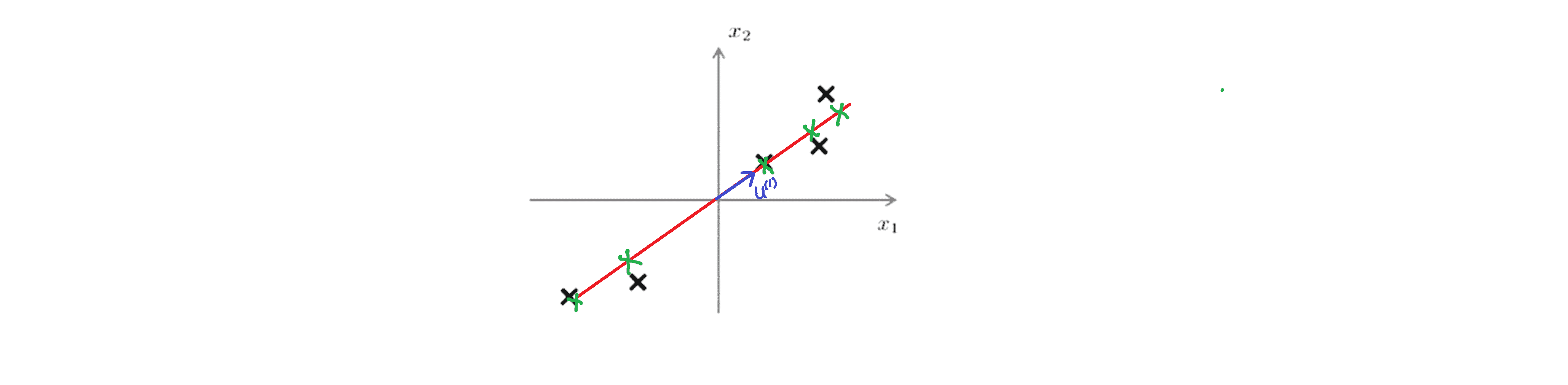
这就是将二维数据降到一维的例子。更一般的情况是我们有 n 维的数据想降到 k 维,在这种情况下我们不仅仅只寻找单个的向量来对数据进行投影,而是要找到 k 个方向来对数据进行投影从而最小化投影误差。
下面是一个例子,如果我们有一些三维数据点:

我们要做的是是寻找两个不共线的向量,比如叫做 u(1) 和 u(2),这两个向量一起定义了一个平面,或者说定义了一个二维面:
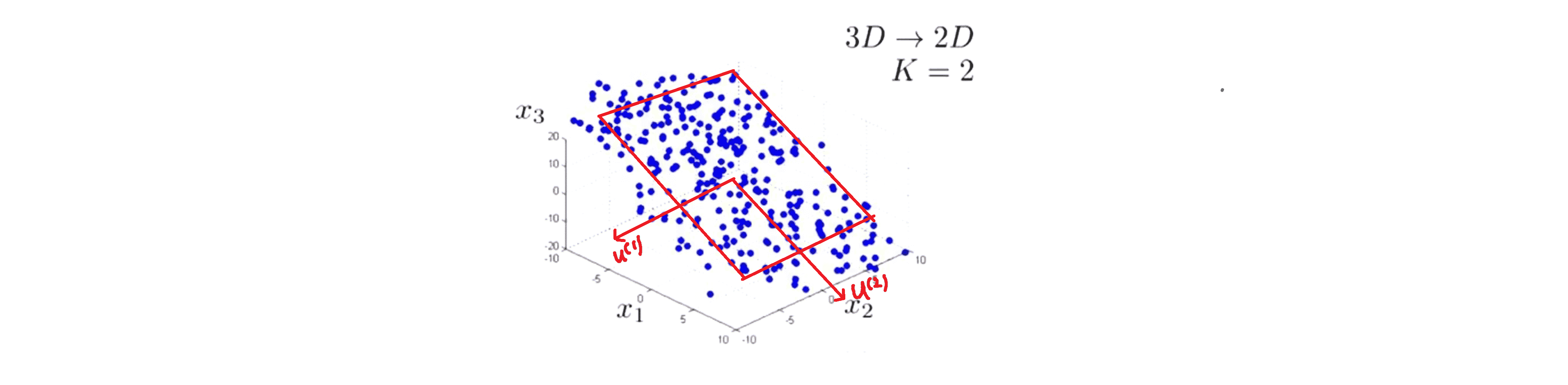
然后我们就将把数据投影到上面,并计算投影误差:
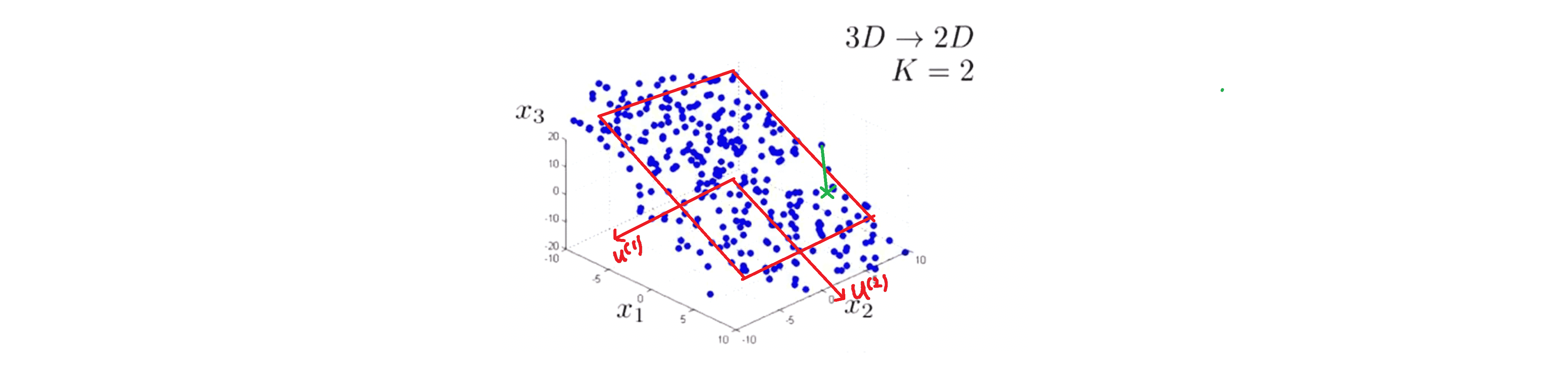
对于一些熟悉线性代数的人来说,你们应该知道对这个正式的定义是我们将寻找一组线性无关的向量 u(1) u(2) …… u(k),我们将要做的是将数据投影到这 k 个向量张成的子空间上。
因此更正式一点的说,在PCA中我们想做的就是寻找到某种方式对数据进行投影进而最小化投影距离。最后提一下一个蛮令人疑惑的问题就是 PCA 和线性回归有怎么样的关系?因为当我们理解 PCA 的时候我们画出的图看上去有点像线性回归有点类似。但是事实是 PCA不是线性回归,尽管看上去有一些相似但是它们确实是两种不同的算法。
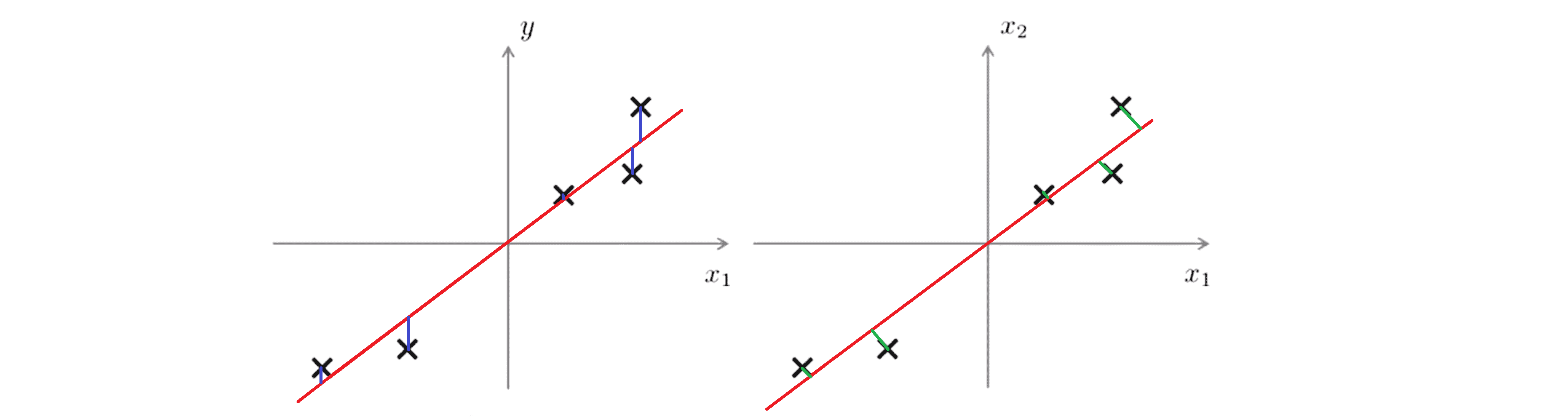
如果我们做线性回归,我们做的是下图左边这样,在给定某个输入特征 x 的情况下,预测某个变量 y 的数值。因此对于线性回归我们想做的是拟合一条直线来最小化点和直线之间的平方误差,所以我们要最小化的是这些蓝线幅值的平方; 与此想反PCA要做的是最小化这些绿色直线的幅值:
更更一般的是当我们做线性回归的时候,总会有一个特别的变量 y 是我们将要预测的,在线性回归中我们要用所有的 x 来预测 y;然而在 PCA 中,没有这么一个特别的或者特殊的变量 y 是我们要预测的,我们所拥有的是 特征x1 x2 等一直到xn,所有的这些特征都是被同样地对待。比如在刚刚的例子中,如果我有三维数据:

我们有3个特征 x1 x2 x3,所有的这些都是被同样地对待,没有特殊的变量 y 需要被预测。因此 PCA 不是线性回归,尽管有一定程度的相似性使得它们看上去是有关联的,但它们实际上是非常不同的算法。
因此通过这一部分希望你们能理解 PCA 是做什么的,你应该已经清楚地了解到PCA是寻找到一个低维的平面对数据进行投影以便最小化投影误差的平方。在下一部分中我们将开始讨论如何真正地找到这个低维平面来对数据进行投影。
实现PCA算法
这一部分就让我们来具体看看主成成分分析(PCA)的算法的实现过程,并且应用 PCA 来给进行数据降维了。
在之前提到过,使用 PCA 之前我们通常会有一个数据预处理的过程,比如我们在拿到某组有 m 个无标签样本的训练集后,我们一般先进行均值归一化 (mean normalization)处理,然后还可以进行特征缩放 (feature scaling)。这根据我们的数据而定跟我们之前 在监督学习中提到的均值归一和特征缩放本质上是一样的,只不过现在我们针对的是一系列无标签的数据 x(1) 到 x(m):

根据代码我们知道,对于均值归一我们首先应该计算出每个特征的均值 μ 然后我们用 x - μ 来替换掉 x 这样就使得所有特征的均值为0。然后由于不同特征的取值范围都很不一样,我们可以把每个特征进行缩放使其处于同一可比的范围内。所以对于某个数据 x(i)j ,我们设平均值为μj,我们就可以用 x(i)j - μj / sj 来替换掉第 j 个特征x(i)j,其中这里的 sj 表示特征 j 的某个量度范围,因此它可以表示最大值减最小值。
进行完以上这些数据预处理后,接下来就正式进入 PCA 的算法部分。在上一部分中,我们已经学习了 PCA 的原理,PCA 是在试图找到一个低维的子空间然后把原数据投影到子空间上并且最小化平方投影误差的值或者说投影误差的平方和,也就是这些绿色线段长度的平方和:
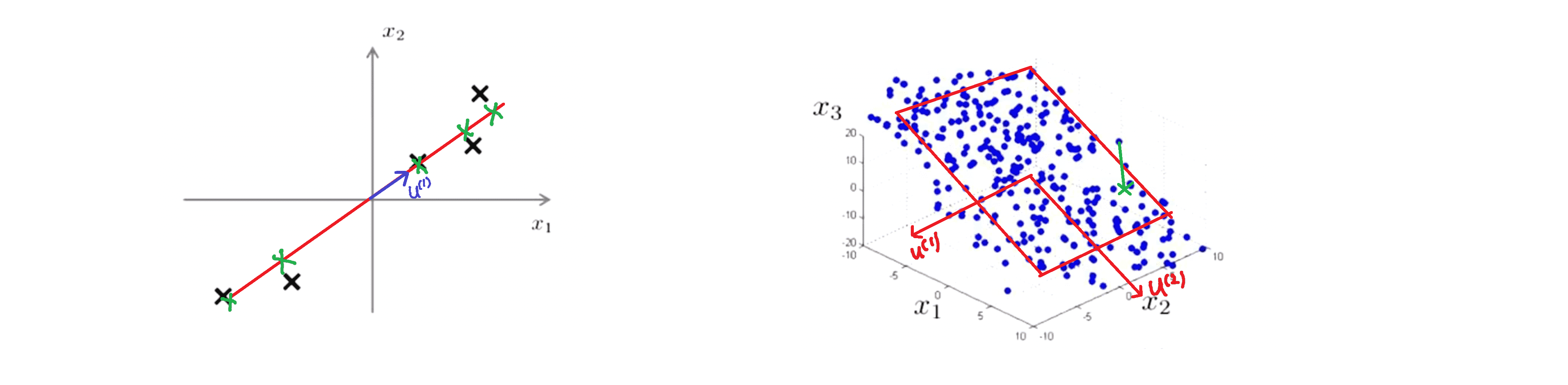
因此我们想要做的是在降维到 1D 的情况下找到某个具体的向量 u(1) 指定这条投影线的方向,或者在降维到 2D 的情况下找到两个向量 u(1) 和 u(2) 来定义一个投影平面对数据进行投影。
我们再来回忆一下降低数据的维度是什么意思,对于上图中左边这个例子,我们的数据是二维实数 x(i) 我们想要做的 是找到一系列一维实数 z(i) 来表示我们的数据,因此这就是从二维降低到一维的意思。具体来说就是要把数据投影到这条红线上,这样我们就只需要一个数来指明点在线上的位置 ,把这个数称为 z 或者 z1。这里的 z 就是一个实数等于是一个一维向量。
所以总的来说 PCA 要做的事就是就是要得到一种方法来计算两个东西:其一是计算这些向量比如上图中左边的 u(1) 和右边的 u(1) u(2);其二是计算出这些数据点在新的变量上的表示,即z1,z2……是多少,也就是我们如何用 u(1) u(2)…… 来计算这些值。
实际上这个问题有它在数学上的推导或者说有完整的数学证明来解释什么才是 u(1) u(2) z1 z2 的正确值,在折柳就不做推导了,感兴趣的同学可以自行学习线性代数相关知识。我们现在只简单学习一下要实现 PCA 要如何计算向量 u(1) u(2) 以及每个点投影后的坐标值 z 。
假如说我们想要把数据从 n 维降低到 k 维,我们要做的首先就是下面这段代码:

可以看到我们首先要做的是计算出这个协方差矩阵,通常我们用希腊字母大写的 ∑ 来表示,假如我们把它存为 Octave 中的一个叫 Sigma 的变量 ,我们接下来需要做的是计算出 Sigma 矩阵的特征向量 (eigenvectors)。 在 Octave 中我们可以使用如下命令 来实现这一功能 [U,S,V] = svd(Sigma); 顺便说一下 svd 表示奇异值分解 (singular value decomposition) ,其将矩阵 ∑ 分解出 U,S,V 这三个矩阵。其实我们有很多种方法来计算矩阵 ∑ 的特征向量,如果你线性代数学得很好或者你之前听说过特征向量的话,你就知道矩阵 ∑ 其实是个正定矩阵,所以我们也可以用 Octave 中的另一个 eig 命令来计算特征向量。实际上 svd 命令和 eig 命令将得到相同的结果,但 svd 的数值其实要更稳定一些,所以我们一般会选择用 svd 。
我们再来看几个细节问题,这个协方差矩阵 ∑ 显然是一个 n×n 的矩阵,然后 svd 将输出三个矩阵 U S V 中我们真正需要的是 U 矩阵, U 矩阵实际上也是一个 n×n 矩阵:

如果我们看 U 矩阵的列,实际上 U 矩阵的列元素就是我们需要的 u(1) u(2) ……如果我们想 将数据的维度从 n 降低到 k 维的话,我们只需要提取矩阵 U 的前 k 列向量,这样我们就得到了 u(1) …… u(k),也就是我们用来投影数据的 k 个方向:

剩下的步骤就很简单了通过这个 svd 我们得到了矩阵 U 我们把它的列向量叫做 u(1) 到 u(n),然后我们取出矩阵 U 矩阵的前 k 列,得到一个新的矩阵Ureduce包含 u(1) 到 u(k) 这 k 个列向量。接着我们计算 m 个数据点在降维后的坐标 z 的方法是让 z = Ureduce^T * x就可以了:

这就是 PCA 的全过程,是不是很简单呢?如果你愿意的话也可以自己推导一下这个方法的数学原理。如果你亲自实现这个算法的话你就得到了这个非常有用的降维算法,你能发现它确实能够很好地最小化平方投影误差的值。
结语
通过这篇BLOG,相信你已经掌握了如何通过PCA对数据进行降维。在接下来的BLOG里,我们还将继续看看PCA的更多细节。最后希望你喜欢这篇BLOG!