在之前的BLOG中,我们完成了对监督学习算法的学习,从这篇BLOG开始就让我们迈入无监督学习的殿堂,开始学习无监督学习的相关算法吧!
无监督学习
首先,让我们来复习一下什么是无监督学习?所谓无监督学习,就是我们要从未标记的数据中进行学习, 而不是从已标记的数据中进行学习。现在我想将无监督学习算法与监督学习算法做个对照。
下图是一个典型的监督学习例子:
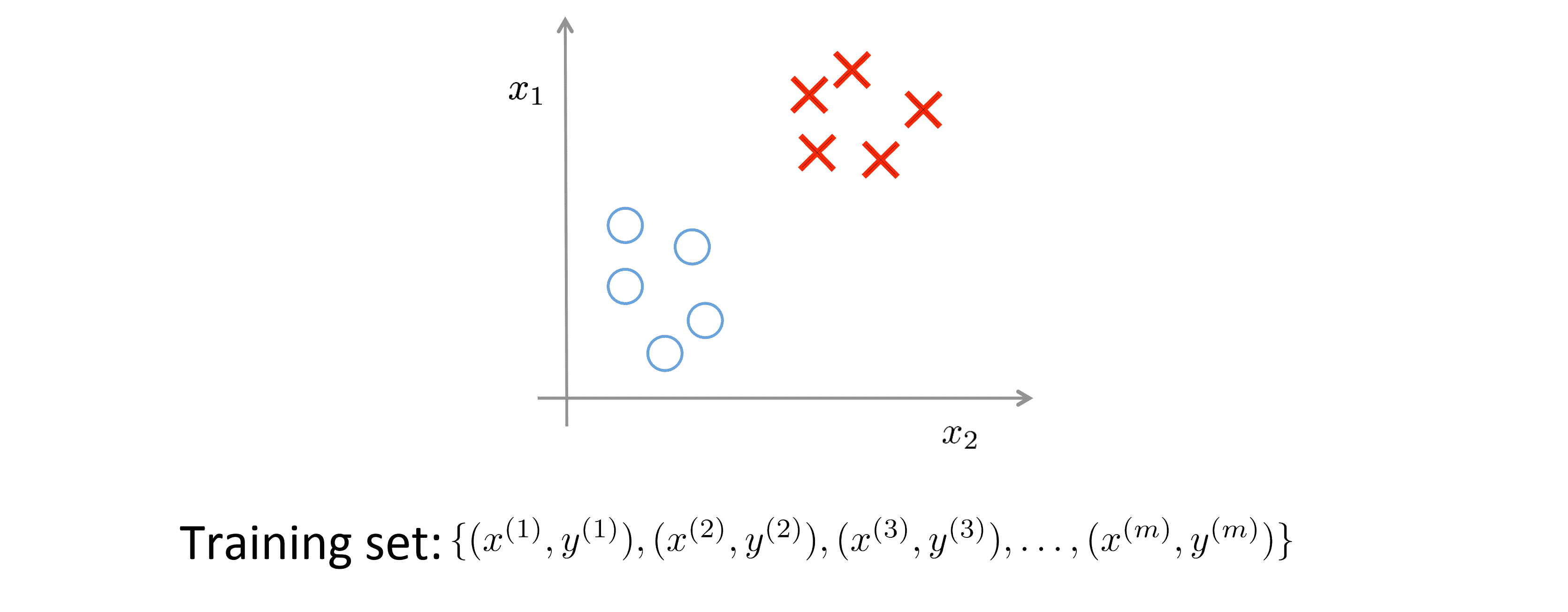
在监督学习中,我们有一组附标记的训练数据集,我们想要找出决策边界,藉此区分开正(positive)或负(negative)标记数据。在这种监督式学习案例中。我们针对一组附标记的训练数据提出一个适当的假设:
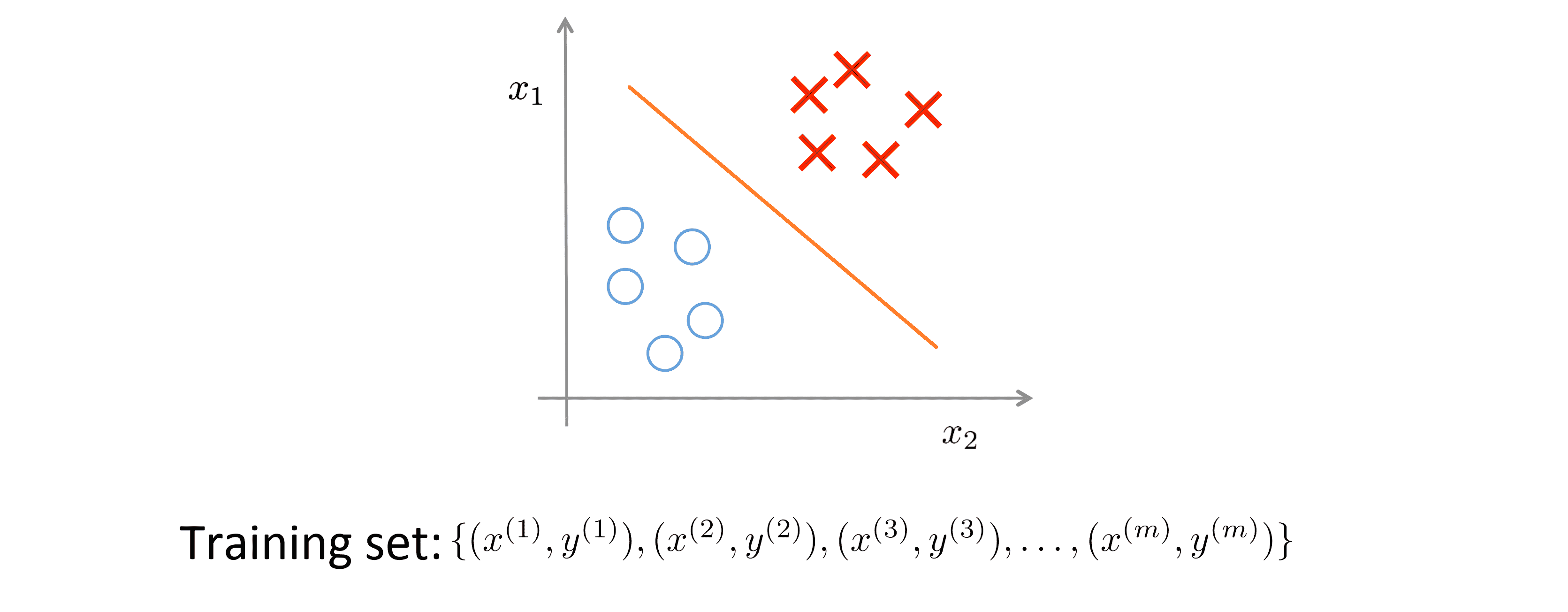
相比之下,在无监督学习案例中我们面对的是一组无标记的训练数据, 数据之间不具任何相关联的标记。 所以我们得到的数据看起来像下图这样:
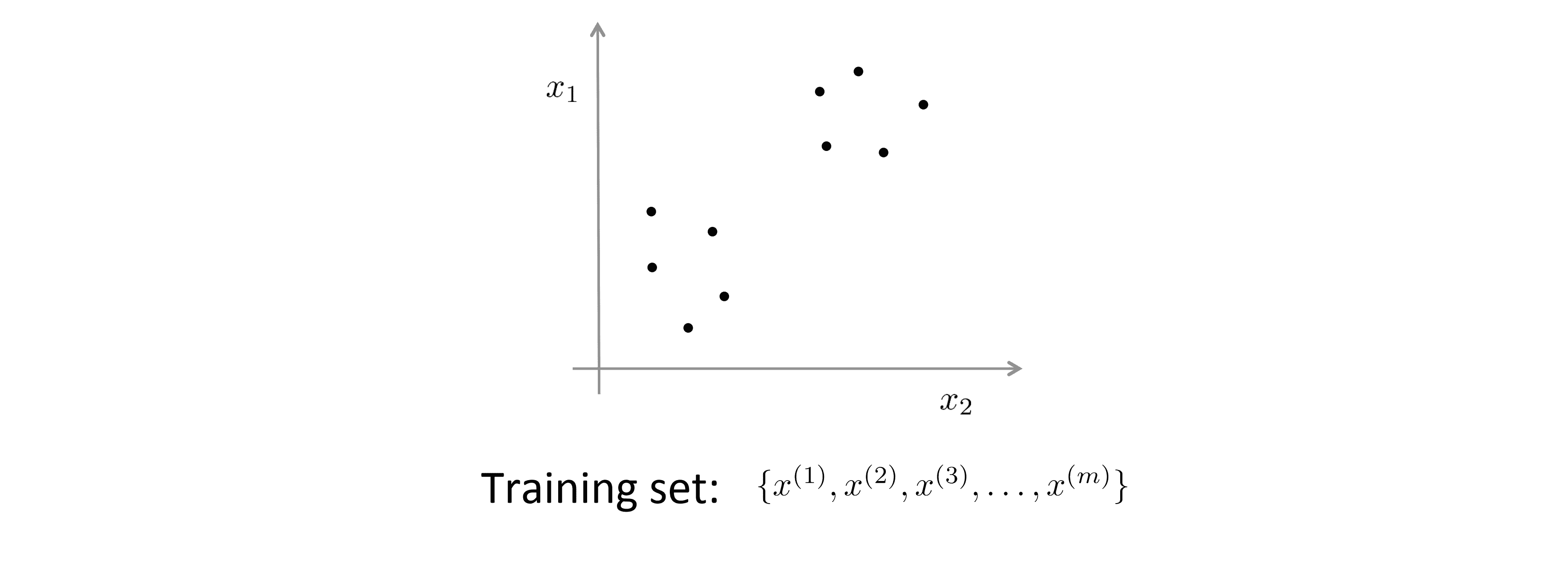
我们拿到的数据集只有一堆数据点,但没有任何标记以供参考。所以从训练数据中,我们只能看到 x1、 x2 …… x(m),但没有任何标记 y 供参考。 所以在无监督学习中, 我们将这种未标记的训练数据送入特定的算法,然后我们要求算法替我们分析出数据的内在联系。就此数据而言,其中一种可能的结构是所有的数据可以大致地划分成 两个类或组:
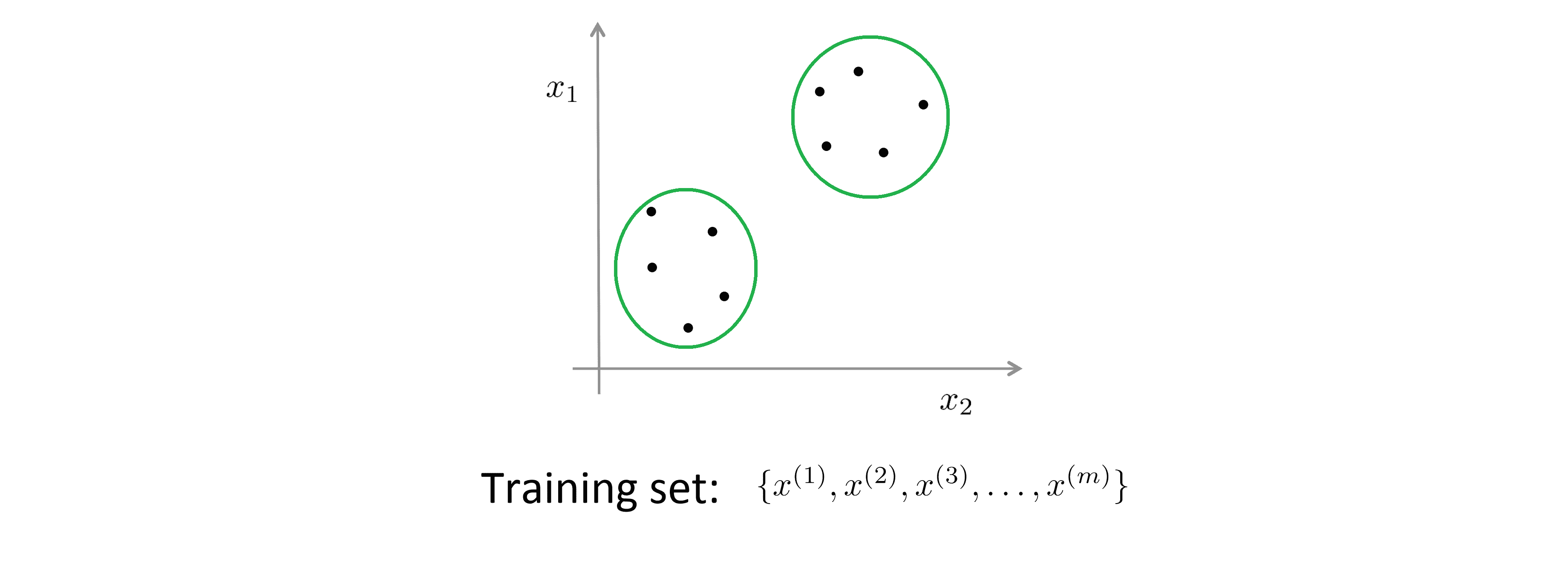
这种划分组的算法一般被称为聚类算法。这是我们现在所见到的第一种无监督学习算法。除此之外,无监督学习还包含 其他各式各样算法,用以寻找其他类型的结构,在之后的BLOG中我们将一一提及。但在目前阶段,我们只需要聚焦于聚类算法。
那么聚类到底有什么什么用呢?在之前的BLOG中我们已经提到几个应用实例:
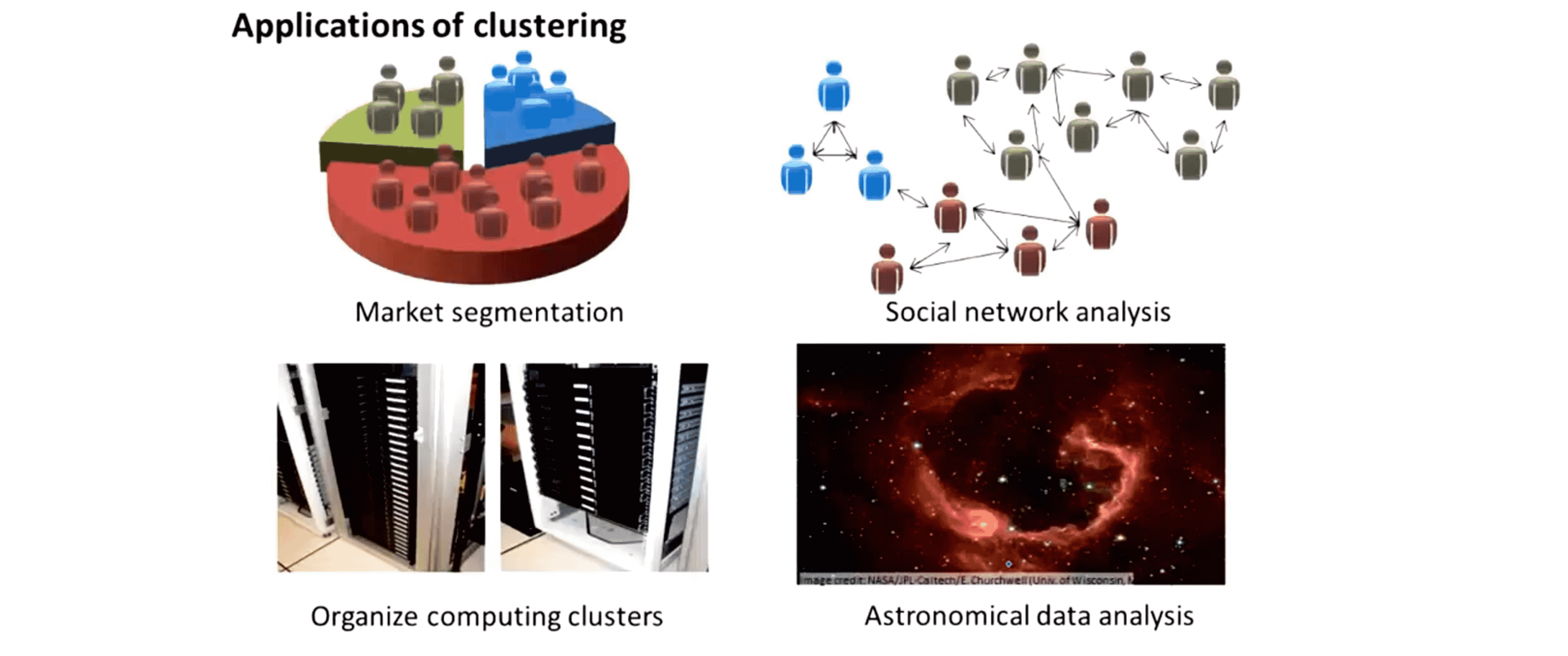
一是细分市场。假设有一个客户数据库,我们想要将所有客户划分至不同的细分市场组, 以便于营销或服务。二是社交划分,即在社交分析体系中,可以查找出一群相互有联系的人。三是在在集群中去看哪些计算机的数据中心倾向于一起工作,你可以用它重新组织您的资源和网络的布局以及数据中心和通信。最后是尝试使用聚类算法去试图理解星系的形成和其中的天文的细节。
总而言之聚类算法是我们无监督学习算法的第一个例子。在下一部分,我们将具体学习一种聚类算法——K-Means算法。
K-Means算法
在聚类问题中,我们的训练集都是未加标签的数据,我们希望能有一个算法去自动地把这些数据分成有紧密关系的子集或是簇。 K-Means 算法(也叫K均值算法)是现在最为广泛使用的聚类方法,在这一部分,我们会一同学习什么是K均值算法以及它是怎么运作的。
K-Means 算法的具体实现步骤最好用图来表达。如图所示假设现在我们有一些没加标签的数据,而我们想将这些数据分成两个簇:
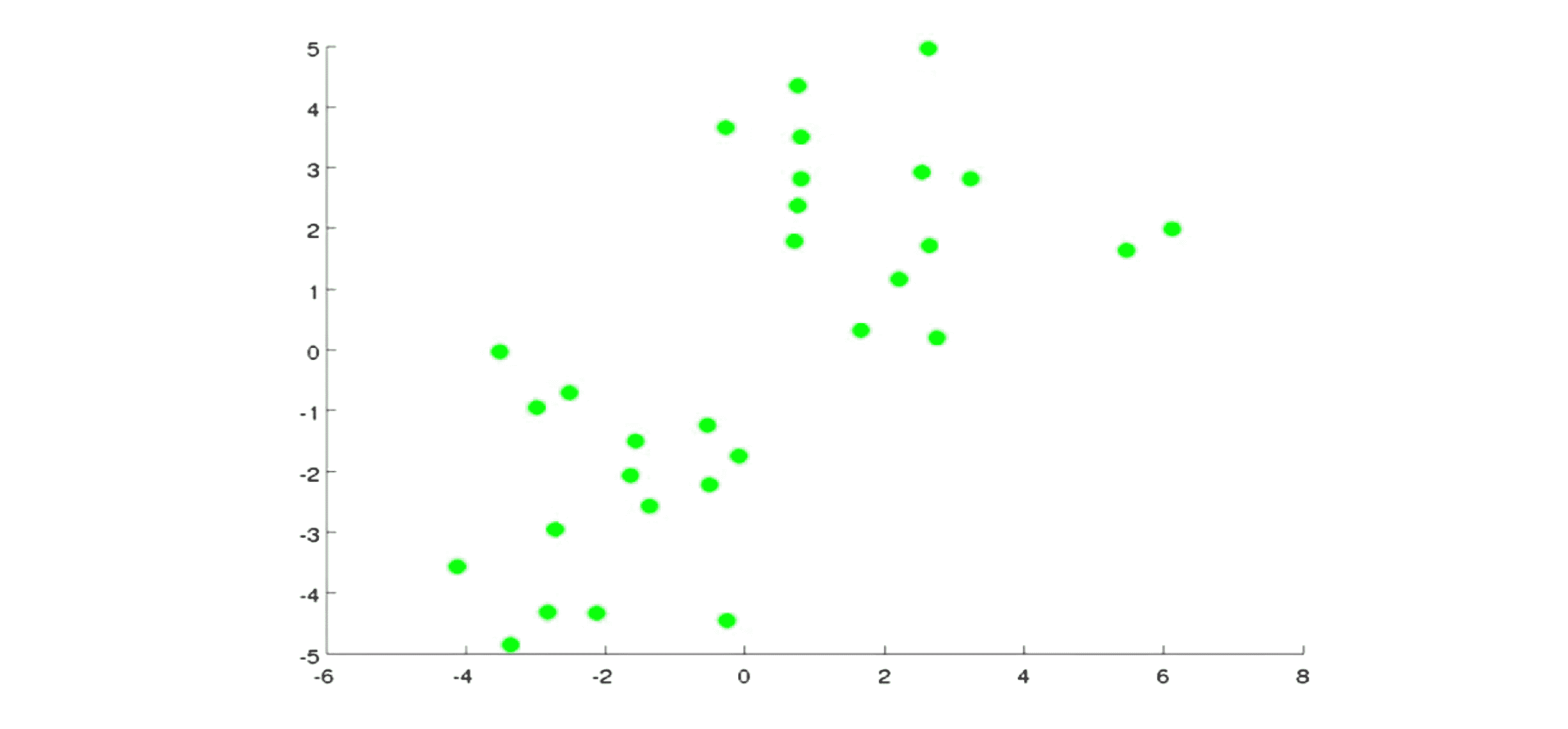
现在我执行 K-Means 算法,方法是这样的:首先我选择两个点(可以直接随机选择),这两个点叫做聚类中心 (cluster centroids),就是下图中的两个叉:
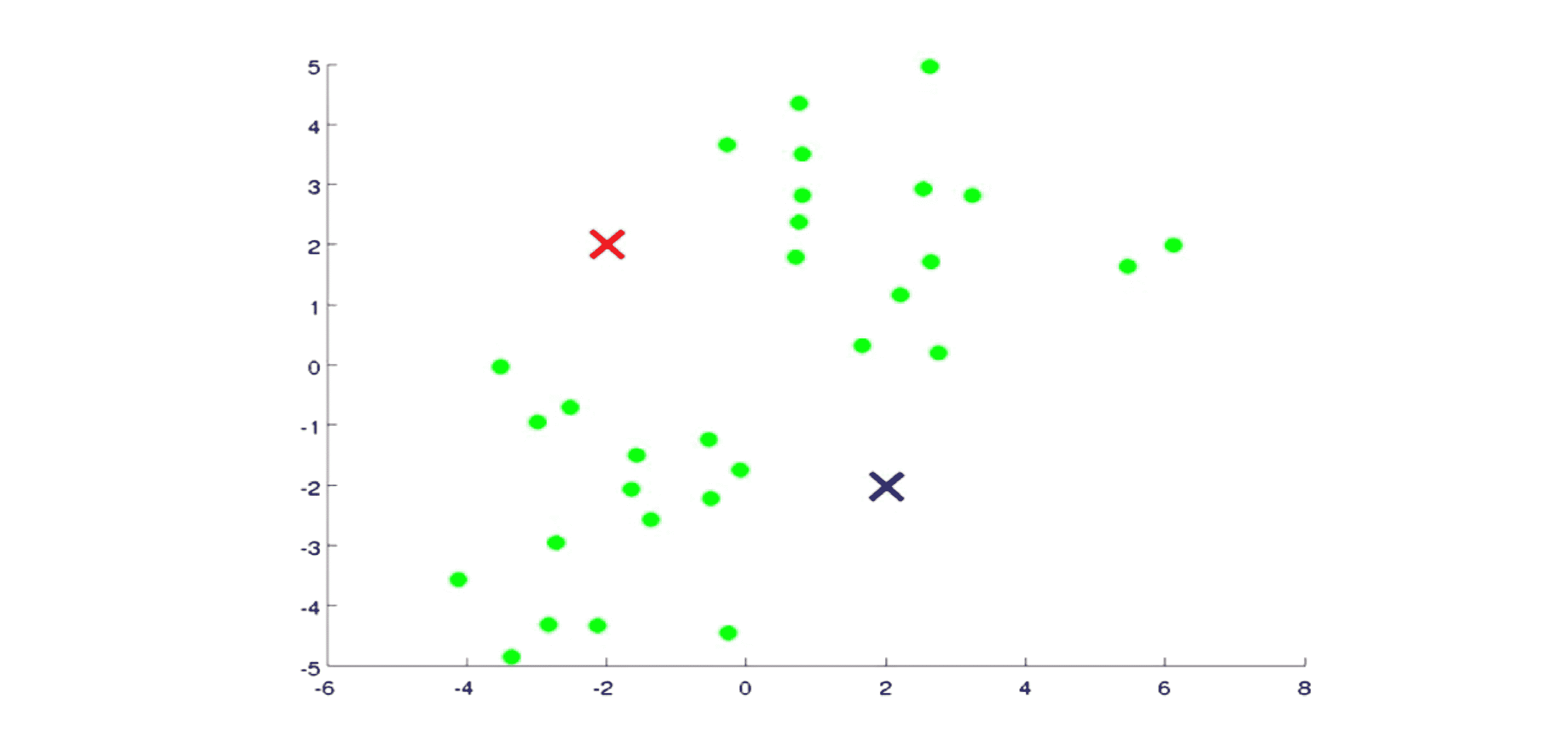
为什么要两个点呢?因为我希望聚出两个类。也就是说想要分成多少类,我们就选择多少个聚类中心。K-Means算法是一个迭代算法,它的每一步迭代都要去做两件事情:第一个是簇分配,第二个是移动聚类中心。
现在我们来具体看看两步是干什么的。在K均值算法的每次迭代中,第一步是要进行簇分配。这就是说我们要遍历所有的样本,也就是我们要把图上所有的绿色的点依据每一个点 是更接近红色的这个中心还是蓝色的这个中心来将每个数据点分配到两个不同的聚类中心中。具体来讲我们对数据集中的所有点依据他们更接近红色这个中心还是蓝色这个中心进行染色。染色之后的结果如图所示:
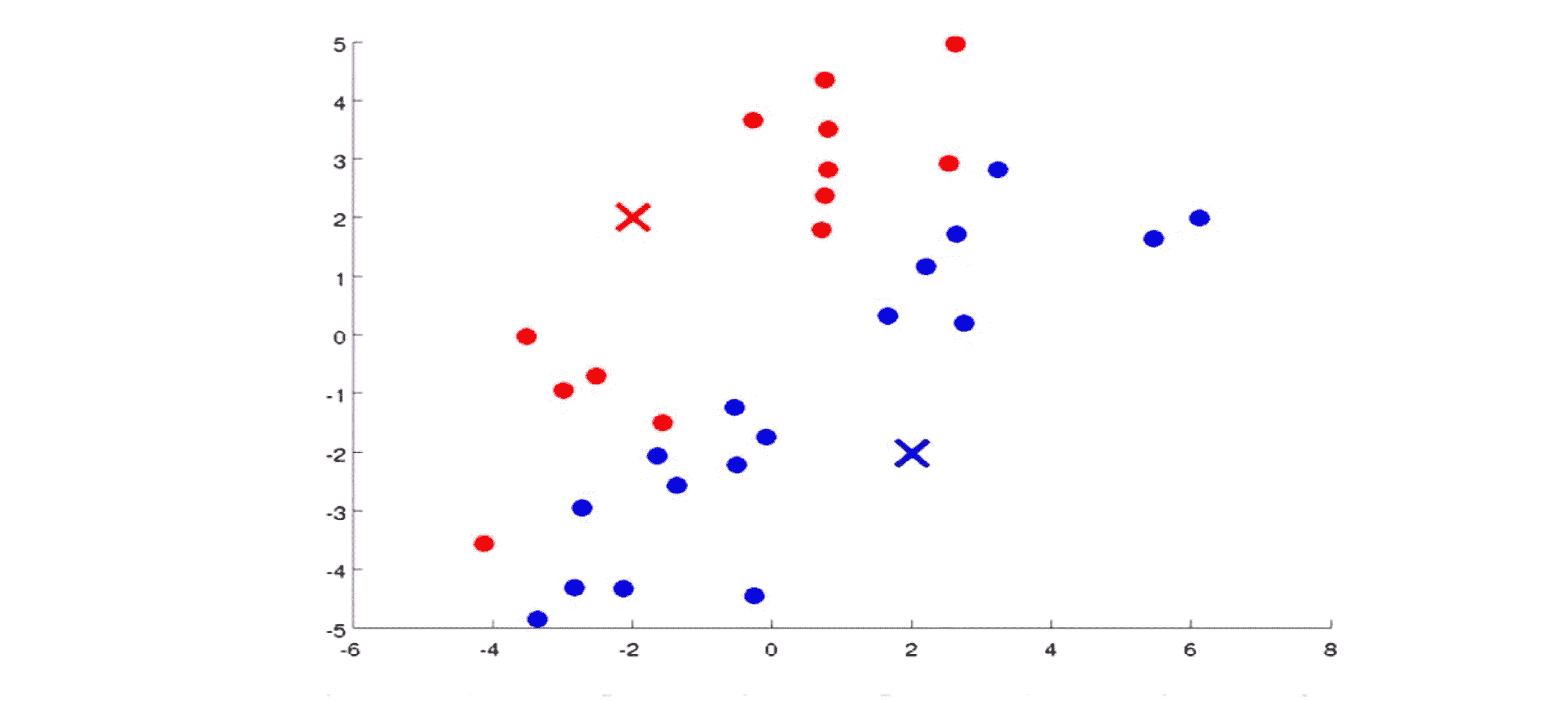
第二步是要移动聚类中心。具体的操作方法是这样的:我们将两个聚类中心也就是说红色的叉和蓝色的叉移动到和它一样颜色的那堆点的平均值处。也就是说我们要做的是找出所有红色的点,计算出它们的平均值,然后我们就把红色点的聚类中心移动到那里。对于蓝色的点也是这样,我们找出所有蓝色的点并计算它们的均值,接着把蓝色的叉放到那里。所以现在两个中心都已经移动到新的均值那里了:
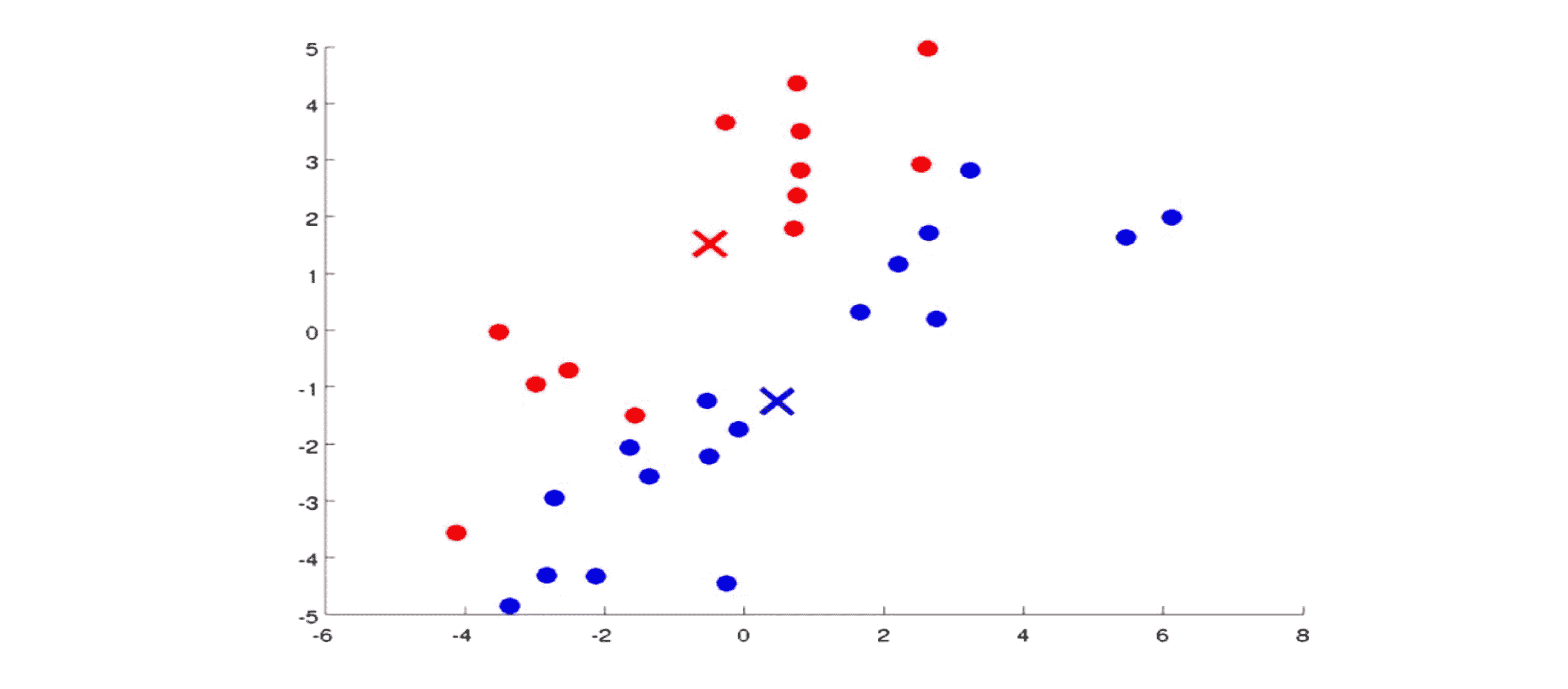
两步都完成后,我们就会进入下一步的迭代。我们重新检查 所有没有标签的样本依据它离红色中心还是蓝色中心更近一些将它染成红色或是蓝色:
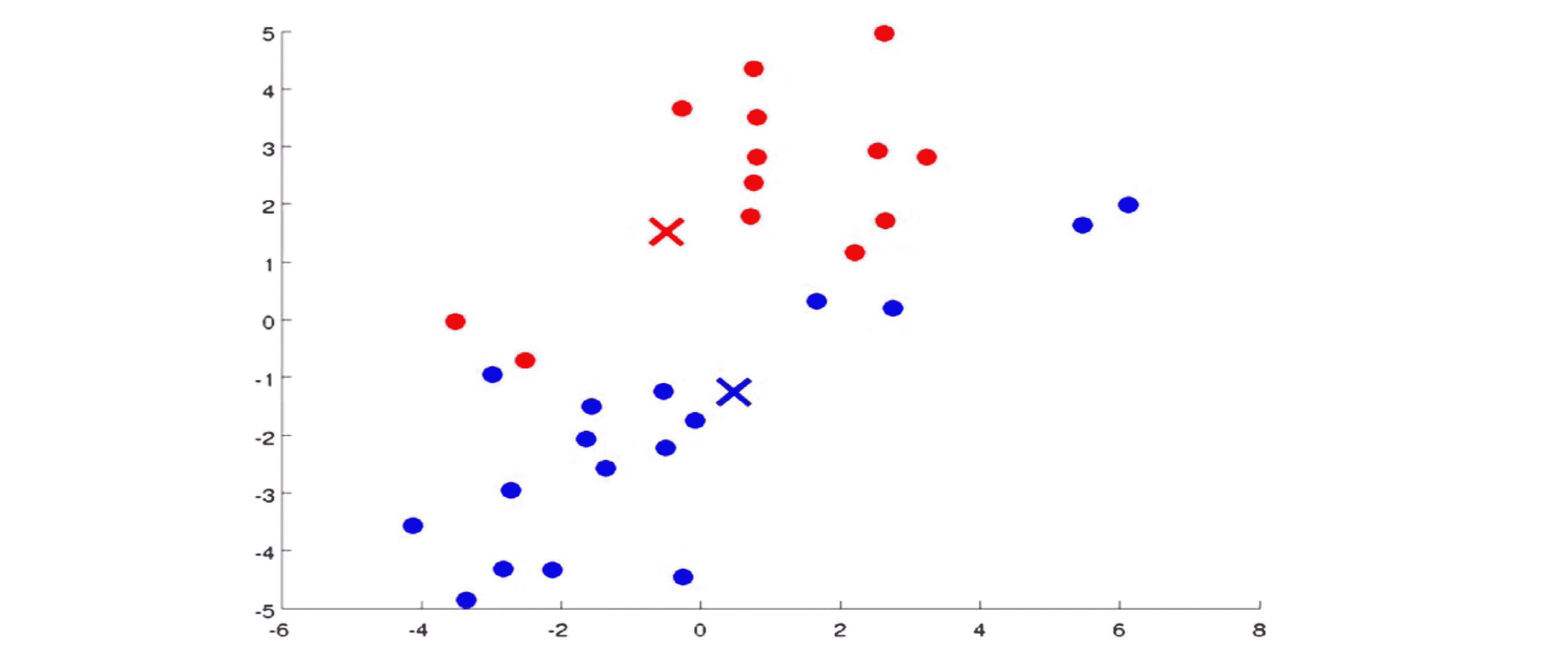
你看某些点的颜色变了,然后我们又要移动聚类中心,也就是我们要计算蓝色点的均值和红色点的均值然后就像图上所表示的一样去移动两个聚类中心:
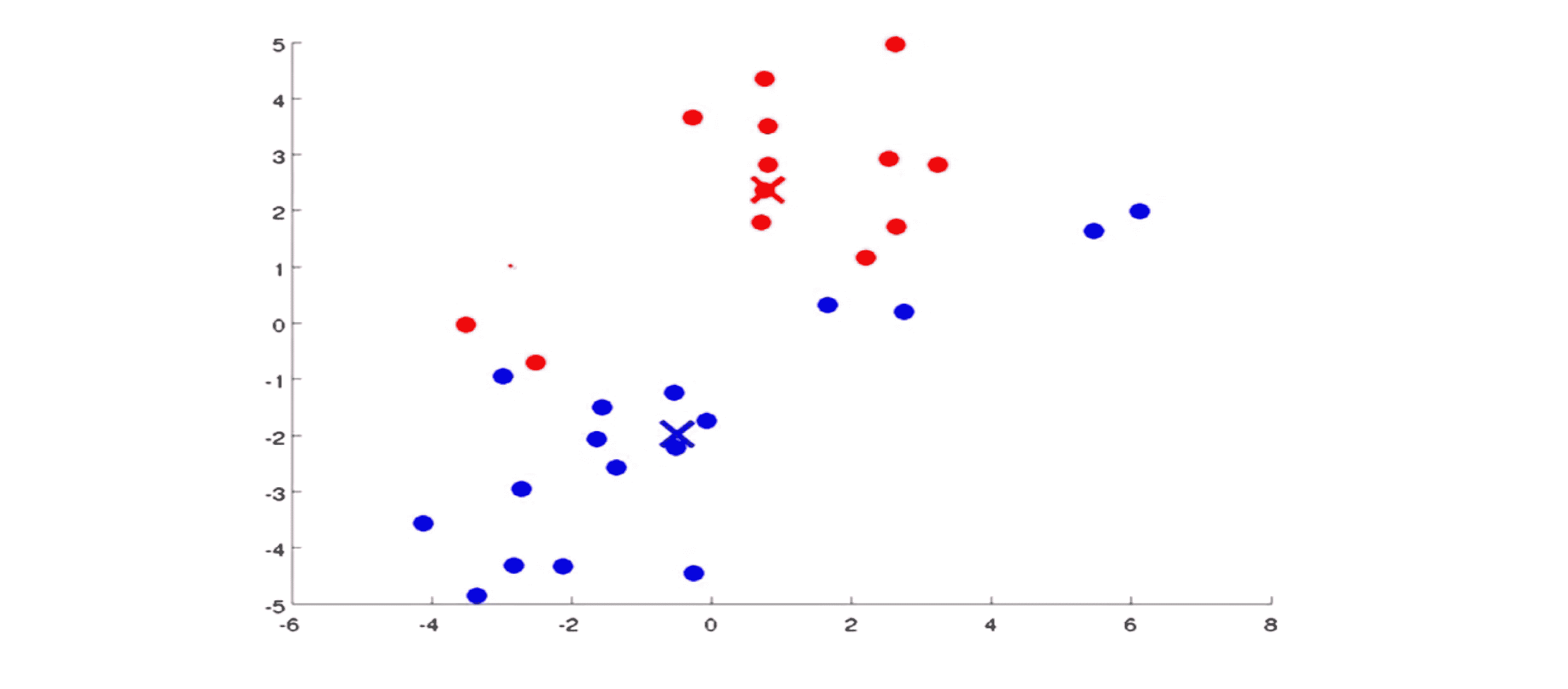
我们再来一遍迭代。我们还是依然根据每个点离哪个中心近将每个点染成红色或是蓝色:
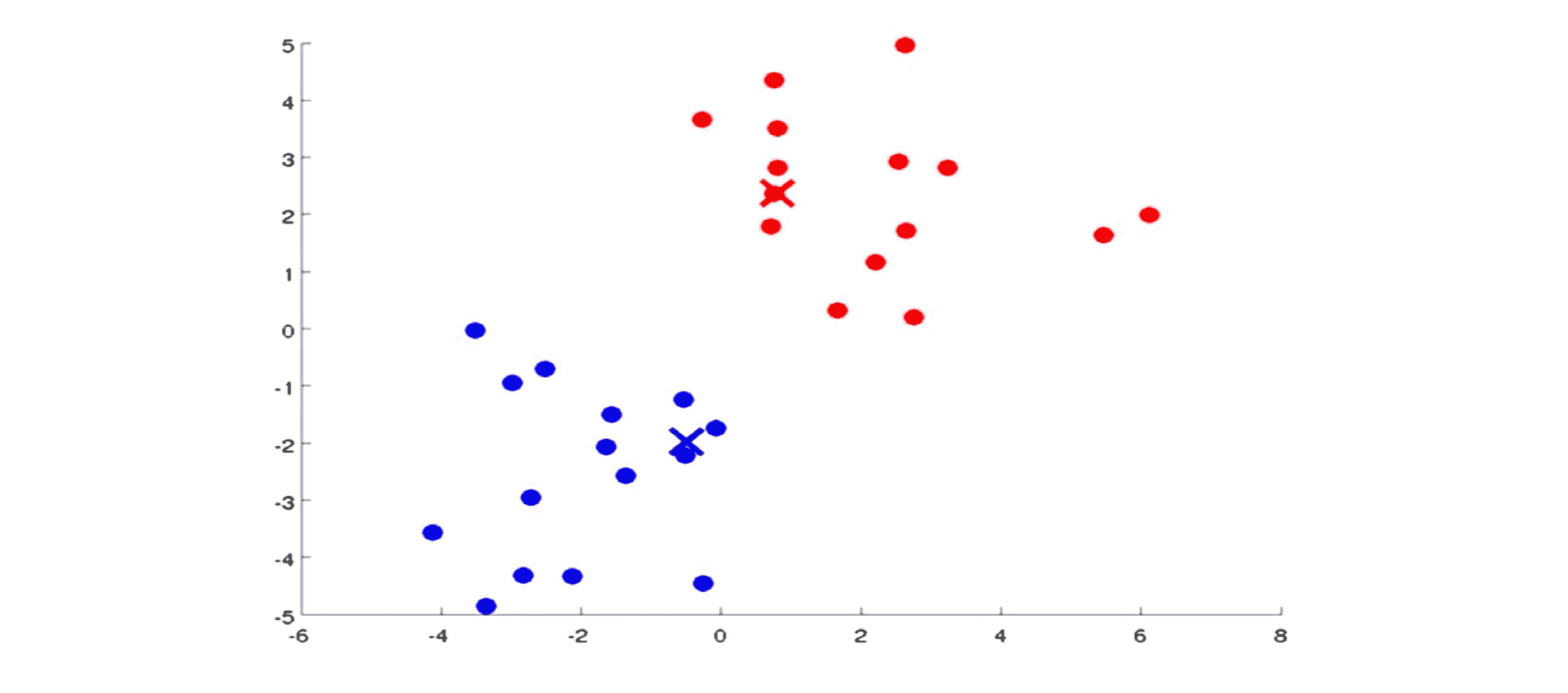
接着我们移动中心:
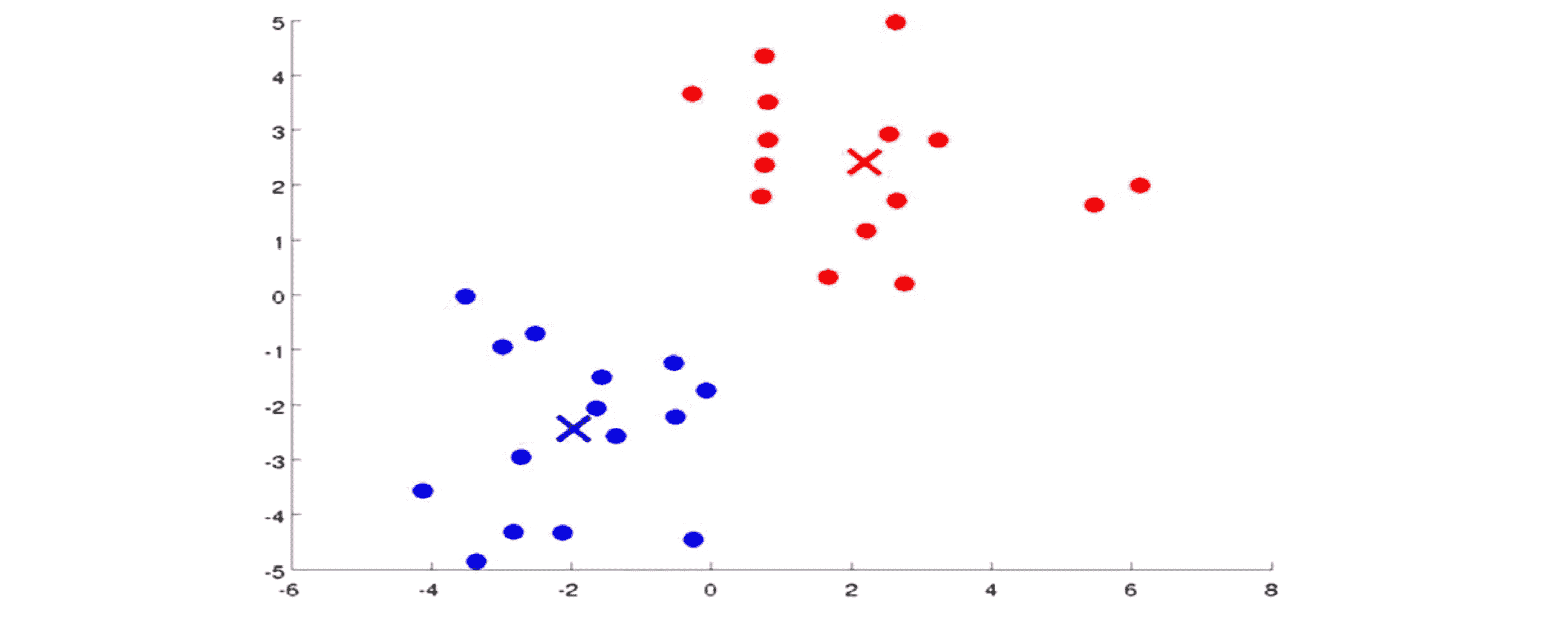
实际上如果我们从这一步开始一直迭代下去聚类中心是不会变的,并且那些点的颜色也不会变。在这时我们就能说 K-Means 算法已经收敛了,它成功地在这些数据中找到两个簇。
让我们用更加规范的格式描述 K-Means 算法。首先 K-Means 算法需要两个输入:第一个是参数 K 表示你想从数据中聚类出的簇的个数;另外一个输入就是只有 x 的没有标签 y 的训练集,因为这是非监督学习我们用不着 y。同时在非监督学习的 K-Means 算法里我们约定 x(i) 是一个 n维向量,也就是我们不需要恒等于 1 的 x0了。
接下来我们来看看 K-Means 算法的代码实现:

我们算法的第一步是随机初始化 K 个聚类中心,记作 μ1, μ2 …… μk。就像之前图中所示聚类中心对应于红色叉和蓝色叉所在的位置。
接下来我们进入 K-Means 算法的内部循环。其中具体实现是这样的:首先第一个 for 循环时对于每个训练样本,我们用变量 c(i) 表示 K 个聚类中心中最接近 x(i) 的那个中心的下标,这就是簇分配的步骤。所以 c(i) 是一个在 1到 K 之间的数。具体来说如果我们想要计算 c(i),那么我要计算出第i个样本 x(i)距离所有K个聚类中心的距离,然后取一个最小值所对应的中心点。接着我们要移动聚类中心,这是说对于每个聚类中心,也就是说在第二个 for 循环中,我们将 μk,也就是第 k 个簇的聚类中心赋值为这个簇的平均值。举个栗子,假如一个聚类中心 μ2 被分配了一些训练样本,像是1,5,6,10 这个表明 c(1) = c(5) = c(6) = c(10) = 2,然后在移动聚类中心这一步中我们要做的是,计算出这四个的平均值即计算 (x(1)+x(5)+x(6)+x(10))/4 然后将其赋值到 μ2 上。假如 x(1) x(5) x(6) x(10) 是 n 维的向量,那 μ2 也是 n 维的向量。既然我们要让μk移动到分配给它的那些点的均值处,那么如果存在一个没有点分配给它的聚类中心 那怎么办? 通常在这种情况下,我们就直接移除,如果这么做了,我们最终将会得到K-1个簇而不是K个簇。但如果就是一定要 K 个簇 不多不少,但是有个没有点分配给它的聚类中心,那我们所要做的是重新随机找一个聚类中心然后一出掉现在这个没有分配点的中心。不过在实际过程 这个问题不会经常出现。
这就是 K-Means 算法,在这个部分结束之前,我们还要一同学习 K-Means 算法的另外一个常见应用来应对没有很好分开的簇。比如说到目前为止我们的 K-Means 算法都是基于一些像下图所示的数据:
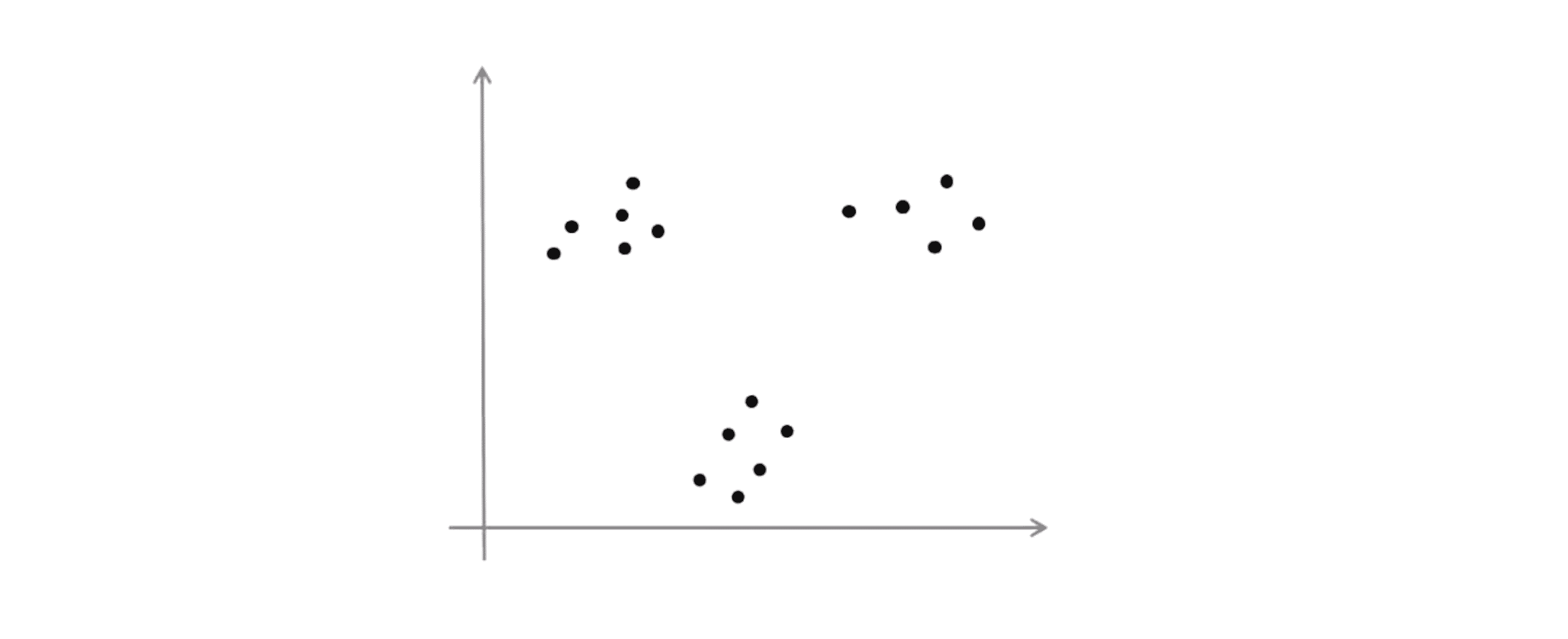
在这组数据中我们有明显的隔离开来的三个簇,然后我们就用这个算法找出三个簇:
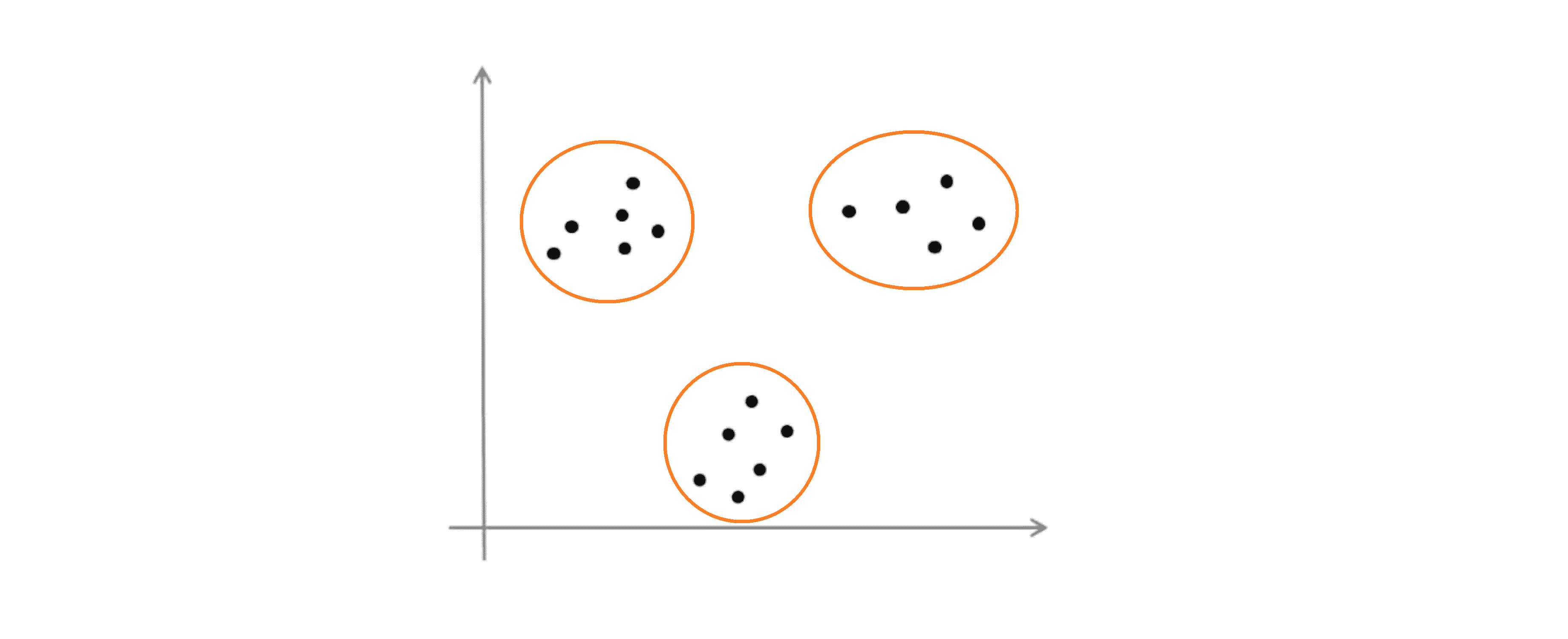
但是事实是 K-Means 算法经常会用于一些这样的数据看起来并没有很好的分来的几个簇。下图一个应用的例子,关于T恤的大小,假设你是T恤制造商,你找到了一些人想把T恤卖给他们,然后你搜集了一些这些人的身高和体重的数据,接着你想确定一下T恤的大小,比如我们要设计三种不同大小的t恤 小号 中号 和大号,那么小号应该是多大的? 中号呢? 大号呢?
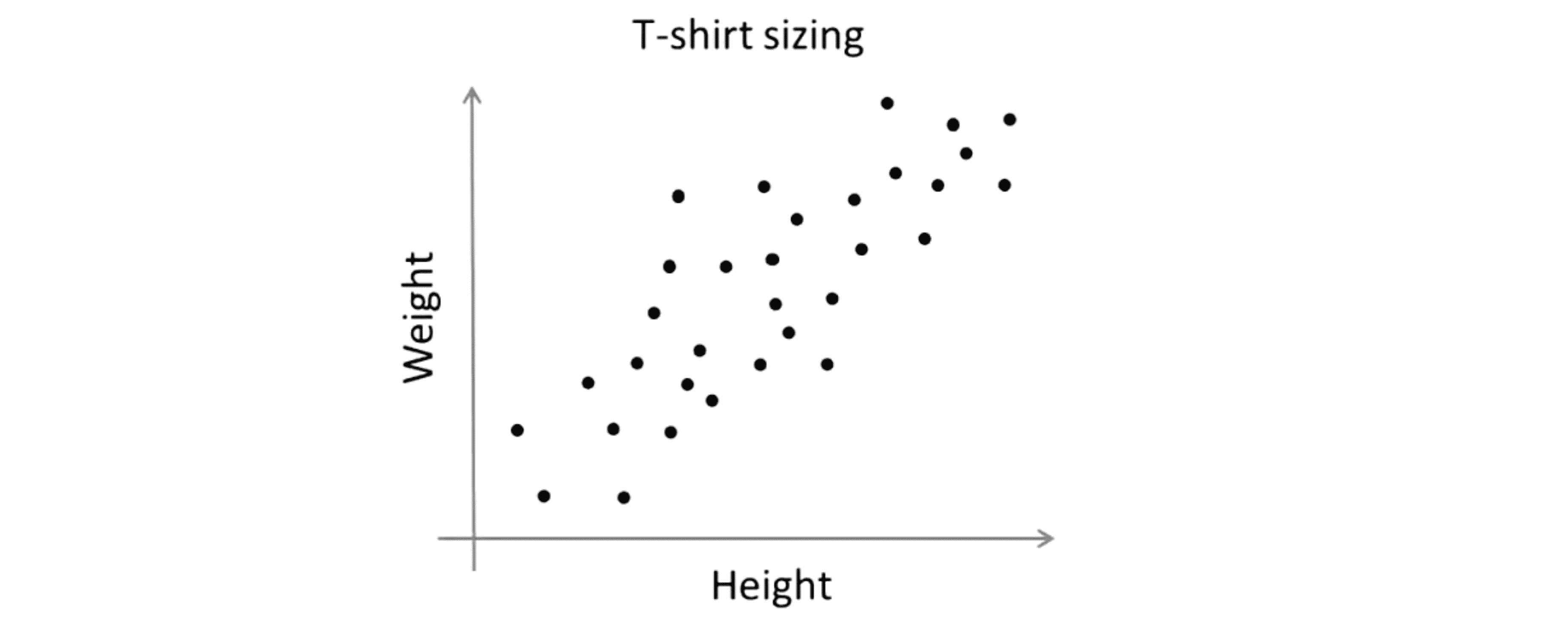
有一种简单的方法就是直接在这样的数据上使用 K-Means 算法进行聚类:
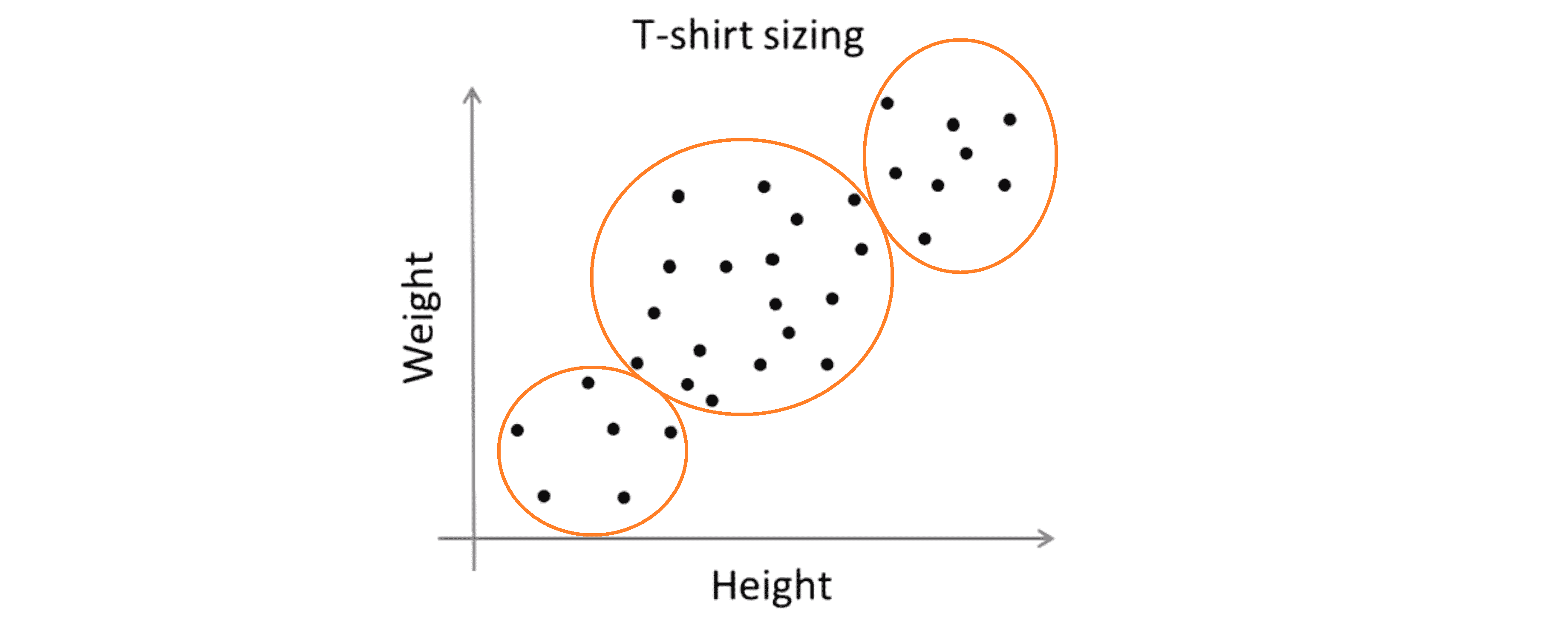
所以说尽管这些数据原本看起来并没有三个分开的簇,但是从某种程度上讲 K-Means 算法仍然能将数据分成几个类。所以你能做的就是对这着人群的分类来设计比较合身的小号衣服,中号的衣服和大号的衣服。这就是一种市场细分的例子,K-Means 算法将你的市场分为三个不同的部分让你就能够区别对待这三类不同的顾客群体来更好的适应他们不同的需求,就像大中小三种不同大小的衣服那样。
以上就是 K-Means 算法的大致步骤。相信现在你应该已经知道如何去实现 K-Means 算法并且利用它解决一些问题。
结语
通过这篇BLOG,相信你已经初步了解了K-Means算法,再接下来的BLOG中,我们将从细节入手,谈谈K-Means算法的实现上的一些细节问题来让其表现得更好。最后希望你喜欢这篇BLOG。