在在之前的BLOG里，我们一同学习了非监督学习的一种主流聚类算法——K-Means算法，在这篇BLOG中，就让我们来一同学习K-Means算法的实现细节吧。

优化目标

在大多数我们已经学到的监督学习算法中，每一个学习算法算法都有一个优化目标函数或者有某个代价函数需要通过算法进行最小化。事实上K-Means算法也有一个优化目标函数或者所是需要最小化的代价函数。在这一部分，就让我们一同学习K-Means算法的优化目标的相关知识吧。

当K-Means算法正在运行时，有几组变量是值得跟踪跟踪的。首先是 c(i) 它表示的是当前的样本 x(i) 所归为的那个簇的索引或者序号；另外一组变量我们用 μk 来表示，其表示的是第 k 个簇的聚类中心 (cluster centroid)的向量坐标。顺便再提一句，在K-Means算法中我们用大写 K 来表示簇的总数，用小写 k 来表示聚类中心的序号。因此小写 k 的范围就应该是 1 到大写 K 之间。除此以外还有另一组变量，我们用 μc(i) 来表示 x(i) 所属的那个簇 的聚类中心。举个例子吧，假如说 x(i) 被划为了第5个簇 这是什么意思呢？ 这个意思是 x(i) 的序号也就是 c(i) = 5 ，因此 μc(i) = μ5 ，因为这里的 μc(i) 就是第5个簇的聚类中心，而也正是我的样本 x(i) 所属的第5个簇。

有了这样的符号表示，现在我们就能写出K-Means算法的优化目标了，以下便是K-Means算法需要最小化的代价函数：

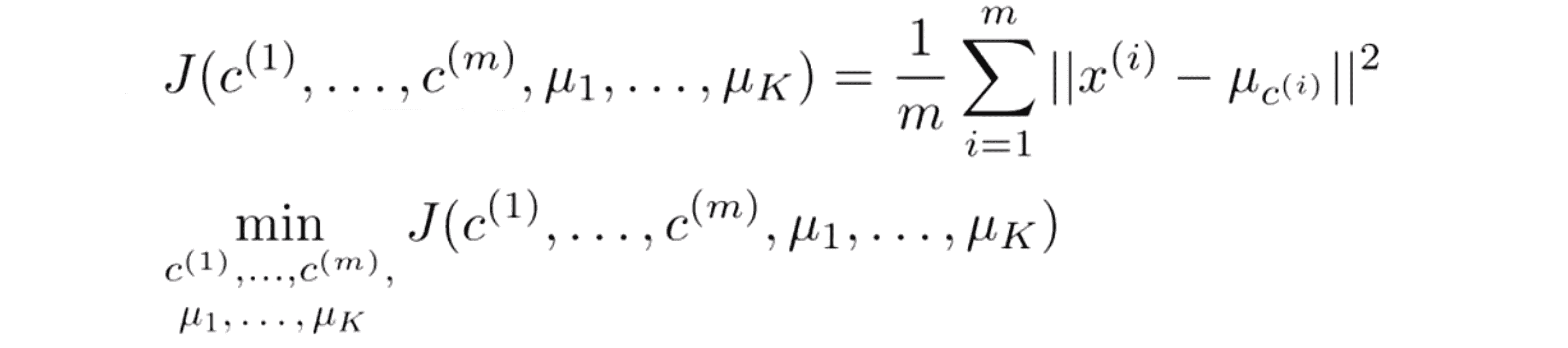
J的参数是 c(1) 到 c(m) 以及 μ1 到 μk，随着算法的执行过程这些参数将不断变化。右边给出了优化目标也就是所有样本 x(i) 到 x(i) 所属的聚类簇的中心距离的平方值的平均数。顺带一提，在K-Means算法中，有时候这个代价函数也叫做 失真代价函数(distortion cost function)。

接下来让我们结合K-Means算法代码进行讲解：

可以用数学证明这个迭代过程实际上就是在对代价函数 J 进行最小化。下面我们来具体看看原因。首先对于迭代的第一步要做的其实不是改变聚类中心的位置去重新选择 c(1) c(2) …… c(m)，这个过程就是把我们的数据点划分到离它们最近的那个聚类中心，因为这样才会使得点到对应聚类中心的距离的和最短，所以第一步有效地使代价函数变小了，也就是说最小化代价函数 J 关于所有点的染色 c(1) 到 c(m)的值。；然后K-Means算法迭代的第二步的任务是让聚类中心的的移动到其染色点的平均值处，在数学上可以轻易地证明这一步是选择了能够最小化 J 的 μ 的值，也就是说最小化代价函数 J 关于所有聚类中心的位置 μ1 到 μK的值。因此K-Means算法实际上是把这两组变量在迭代的两部分中分割开来考虑分别最小化 J。首先是 c 作为变量然后是 μ 作为变量。这就是K-Means算法。

在这一部分我们已经理解了K-Means算法的原理，其运算的目的就是去最小化代价函数 J ，我们也可以用这个原理来试着调试我们的学习算法，保证我们K-Means算法的实现过程是正确的。

随机初始化

在这一部分就让我们聚焦如何在K-Means算法中进行初始化，更重要的是这将引导我们讨论如何避开局部最优来构建K-Means算法的据类。

上图是我们之前就看过很多次的K-Means算法代码，其中我们之前没有讨论得太多的是第一步随机选择聚类中心点的那一步。其实初始化聚类中心有几种常用的的方法，比如像我们之前那样直接随机初始化聚类中心……但是事实证明有一种方法比其他大多数可能考虑到的方法更加被推荐，接下来我们就来重点了解这个方法。

当运行K-Means算法时，我们开始时需要初始化K个聚类中心，K值一般要比训练样本的数量 m 小，因为如果运行一个 K均值聚类中心数量等于或者大于样本数的K-Means算法会很奇怪。人们通常初始化K-Means算法聚类的方法是随机挑选K个训练样本，将它们作为聚类中心设定μ1 到 μk。

让我们来看一个具体的例子，对于下面这样一组数据点：

假设 K = 2， 那么为了初始化聚类中心我们要做的是随机挑选两个个样本作为初始化的聚类中心：

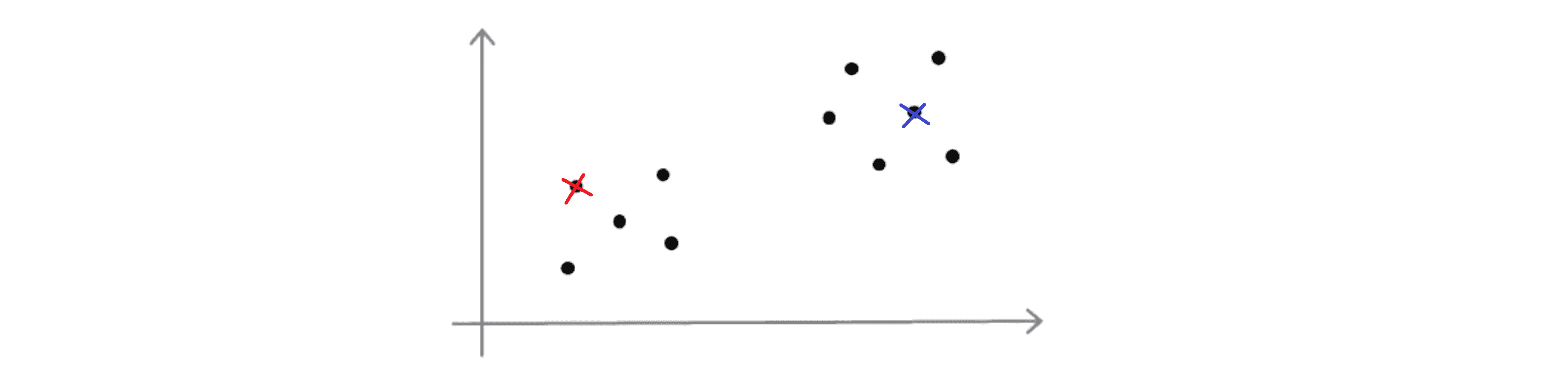
刚刚我们画的看上去是相当不错的一个例子，但是有时候我们可能不会那么幸运也许我最后会挑选下面这两个聚类中心：

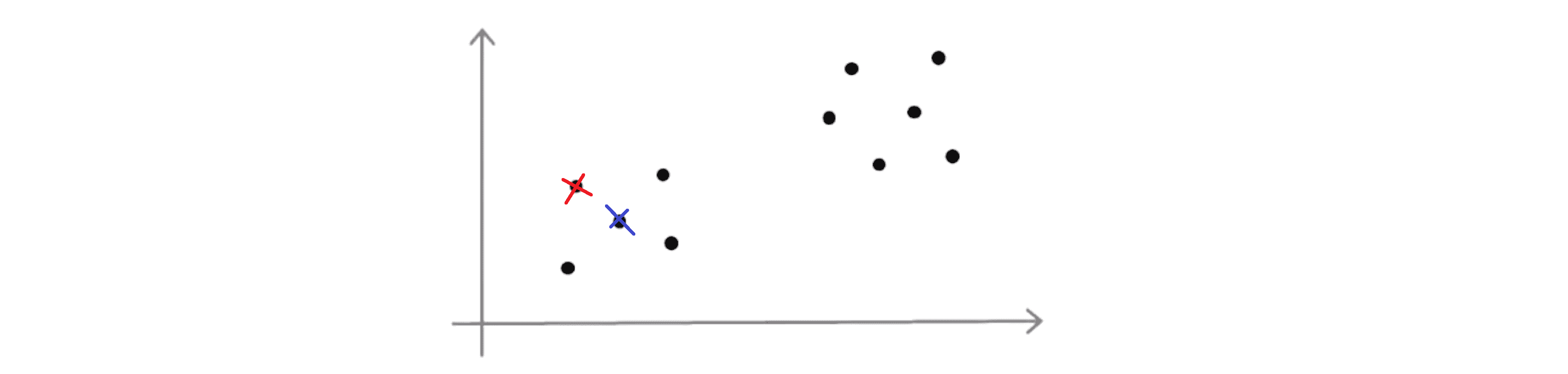
这就是如何随机初始化聚类中心。也许通过上面的两幅图，你已经猜到采用K-Means算法进行聚类最终可能会得到不同的结果。其最终结果往往取决于聚类簇的初始化方法，因此也就取决于随机的初始化。K-Means算法最后可能得到不同的结果，尤其是如果K-Means算法最后收敛在局部最优的时候。

举个栗子吧，假如我们有下面这样的一些数据：

这些看起来好像有 3 个聚类，那么如果我们运行K-Means算法，它最后得到一个局部最优，这可能刚好是真正的全局最优，这样你就会得到下面这样的聚类结果：

但是如果你运气特别不好，随机初始化K-Means算法也可能会卡在不同的局部最优上面，比如下面这两种：

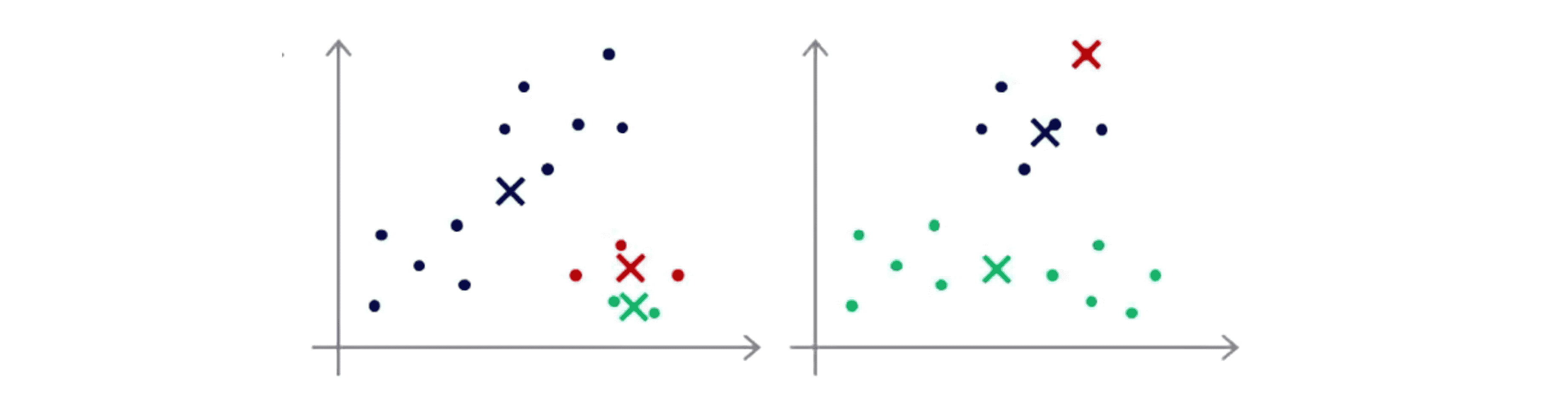
因此如果你担心K-Means算法会遇到局部最优的问题，如果你想提高K-Means算法找到最有可能的聚类的几率的话，就像这上面所展示的，我们能做的就是尝试多次随机的初始化，而不是仅仅初始化一次K均值方法，这样就比较容易得到很好的结果。

具体到代码：

我们能做的是初始化K-Means很多次，并运行K-Means算法很多次，通过多次尝试来保证我们最终能得到一个足够好的结果，一个尽可能局部或全局最优的结果。具体地我们一般执行这个循环 100次，这是一个相当典型的次数数字，有时会是从50到1000之间，最后完成整个过程100次之后，我们会得到这个100种聚类数据的结果，最后我们要做的是在所有这100种聚类的结果中，选取能够给我们代价最小的一个结果。

事实证明，如果我们运行K-Means算法时，如果所用的聚类数相当小比如是从2到10之间的任何数的话，做多次的随机初始化通常能够保证我们得到一个较好的局部最优解，即保证我们能找到非常好的聚类数据。但是如果K非常大的话，那么多个随机初始化就不太可能会有太大的影响，更有可能我们的第一次随机初始化就会给我们相当好的结果，做多次随机初始化可能会给我们稍微好一点的结果，但是不会好太多。

这就是随机初始化的K-Means初始化方法，下一部分我们将聚焦聚类数量继续进行讨论。

聚类数量

在这一部分，让我们来讨论一下K-Means算法的最后一个细节——如何去选择 K 的值。

说实话在这个问题上没有一个非常标准的解答或者能自动解决它的方法。目前用来决定聚类数目的最常用的方法仍然是通过看可视化的图或者看聚类算法的输出结果或者其他一些东西来手动地决定聚类的数目。但我们看看现在人们对这个问题的思考。

尽管最为常见的方法实际上仍是手动选择聚类的数目，选择聚类的数目可能不总是那么容易，大部分原因是数据集中有多少个聚类通常是模棱两可的。比如看到下面这样一个数据集：

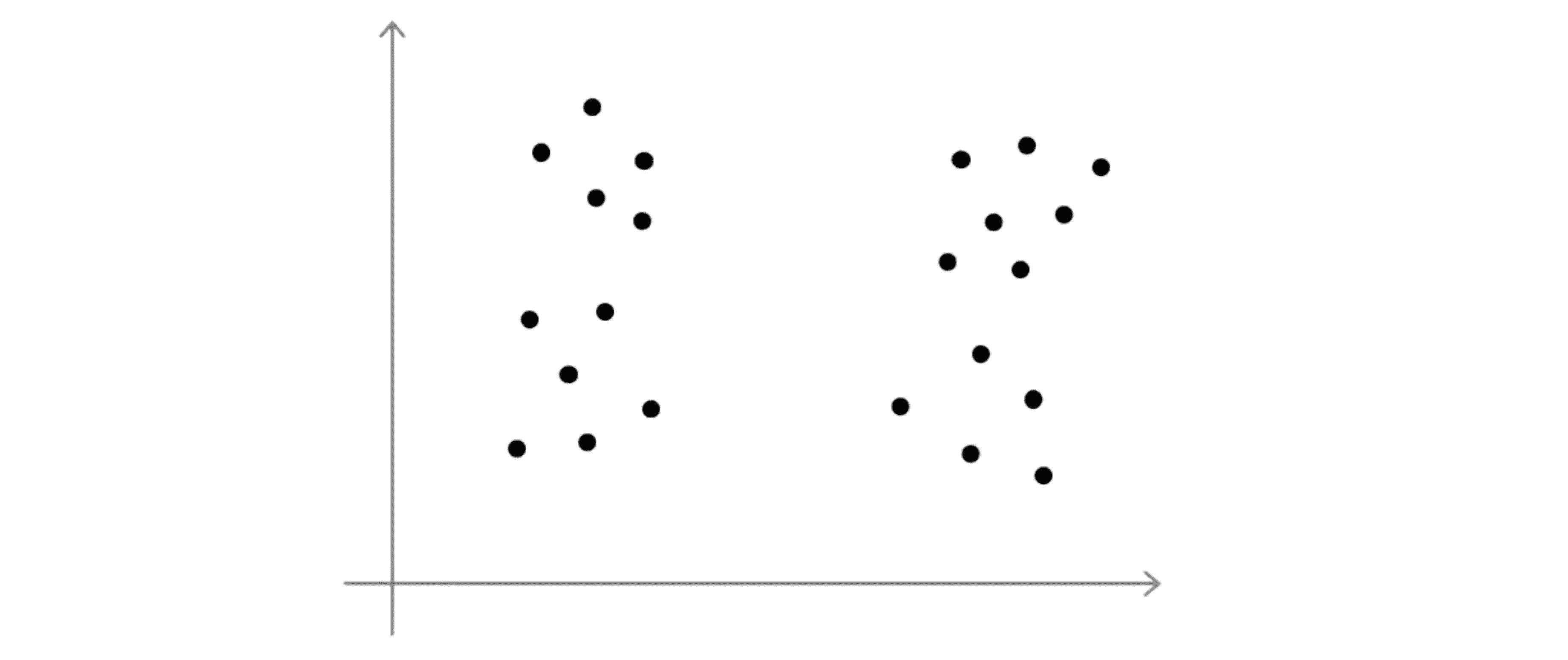
有些人可能会看到四个聚类，那么这就意味着需要使用 K=4：

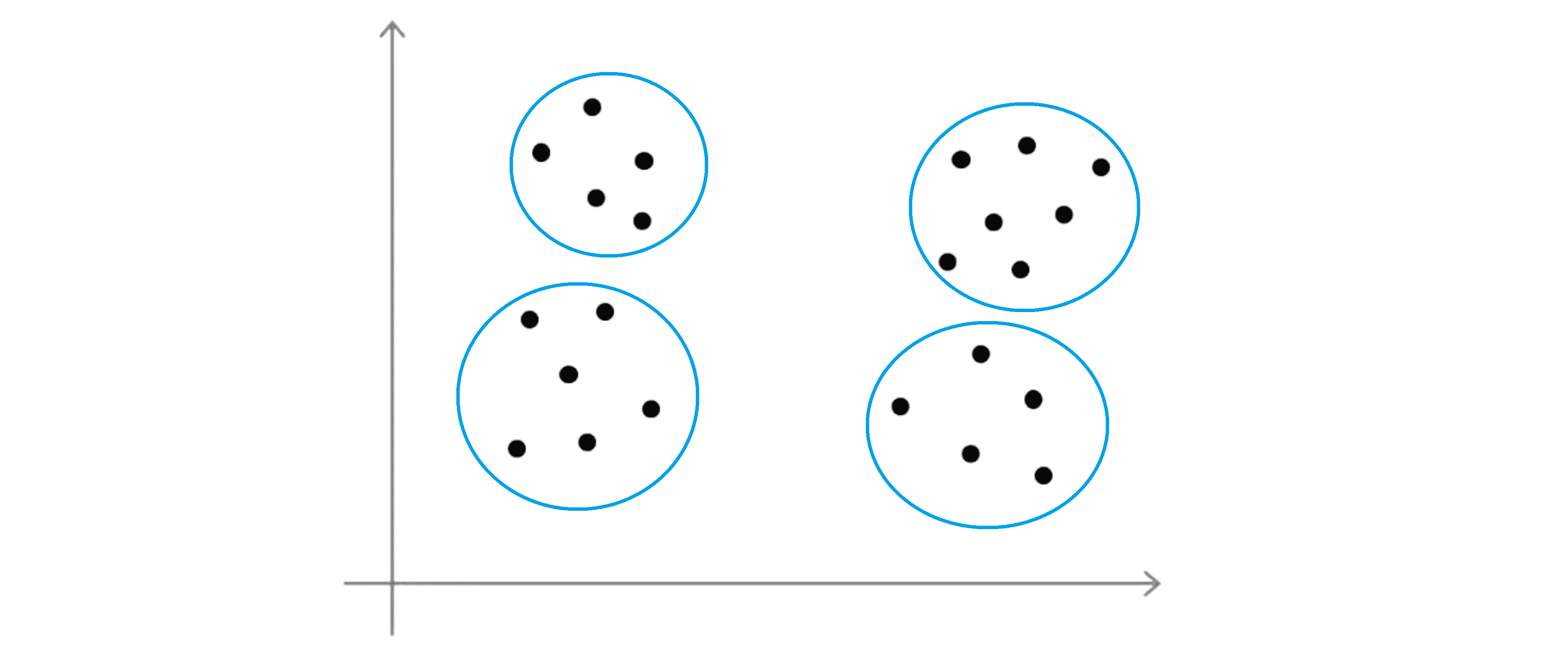
或者有些人可能会看到两个聚类这就意味着 K=2：

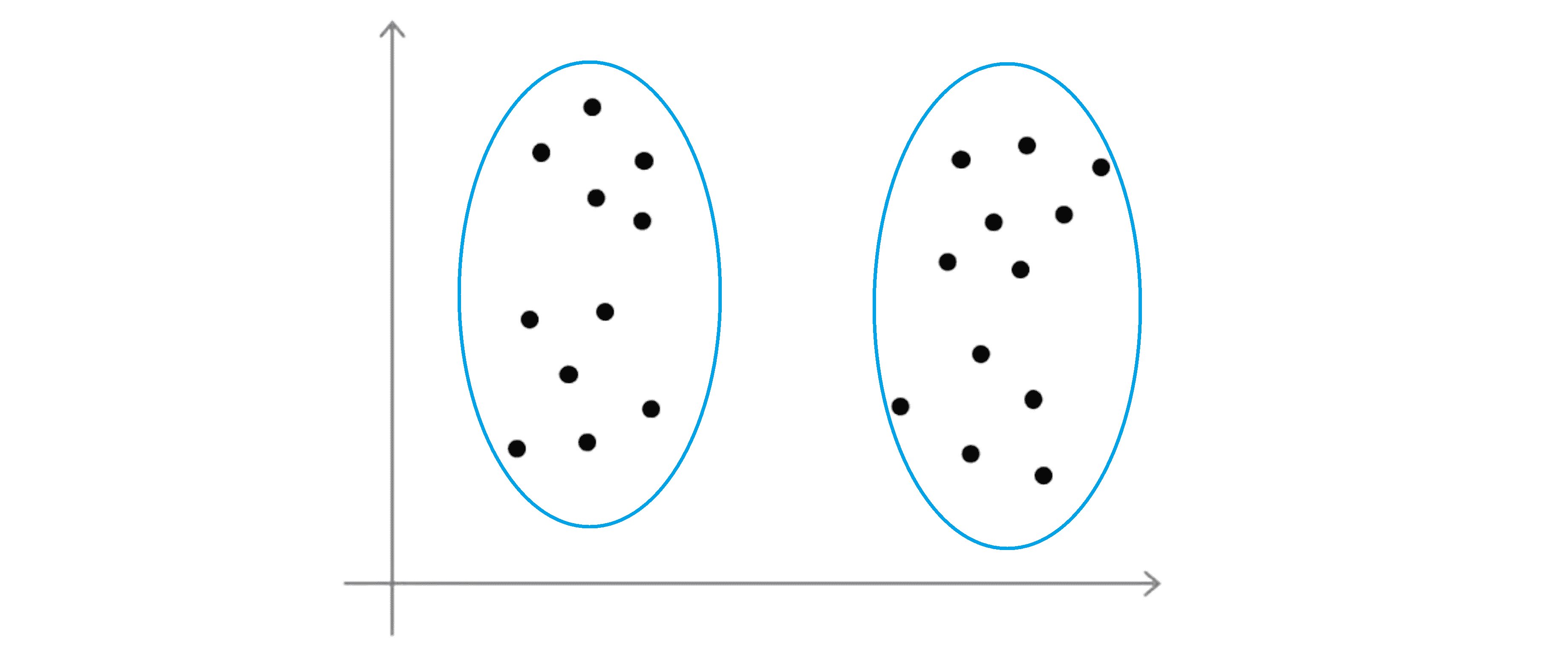
那么看到这样一个数据集，在我看来它的真实的类别数实际上确实是模棱两可的，所以我并不认为这里有一个正确答案。这就是无监督学习的一部分，没有给我们标签所以不会总有一个清晰的答案，这是为什么做一个能够自动选择聚类数目的算法是非常困难的原因之一。

当人们讨论选择聚类数目的方法时可能会提及一个叫做肘部法则 (Elbow Method) 的方法，现在让我们一起来了解一下它，之后会提及到它的一些优点和缺点。那么对于肘部法则，我们所需要做的是改变K的值也就是聚类类别的总数来运行K-Means算法这就意味着，然后计算代价函数 J并将其画在图中。最后我们就能得到一条曲线，它展示了随着聚类数量的增多，我们的代价J是如何下降的。

我们可能会得到下面一条这样的曲线：

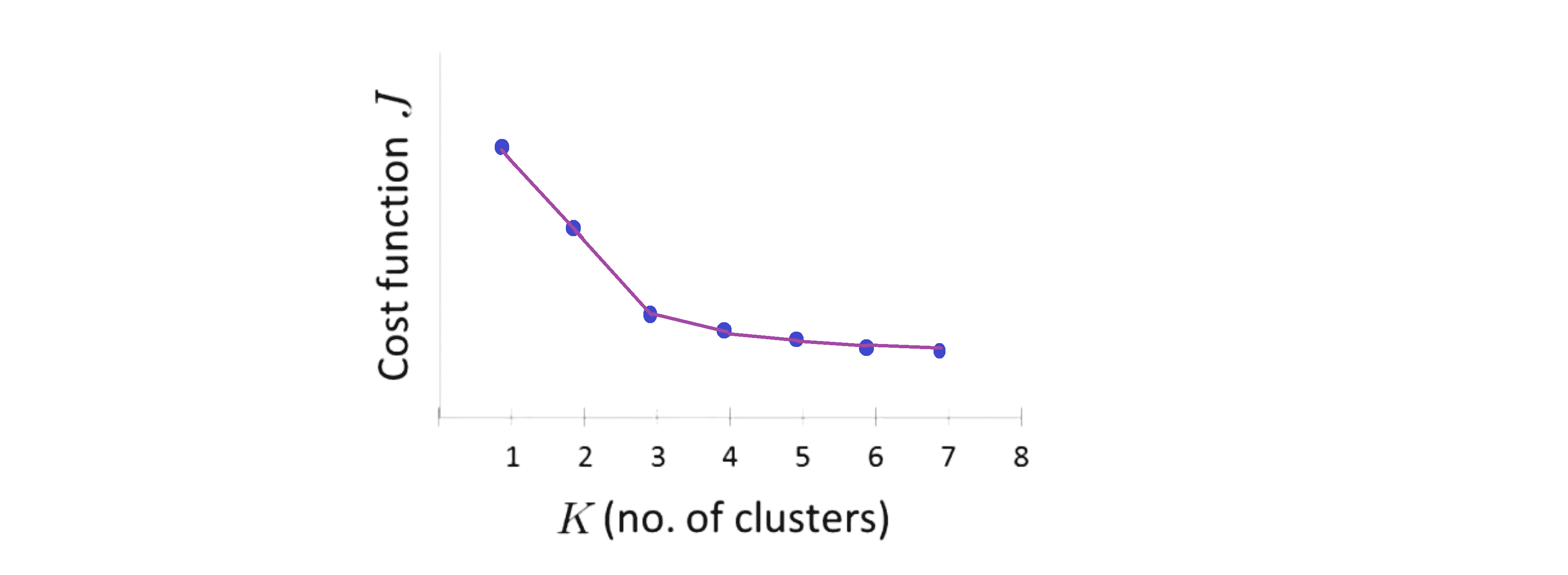
看到这条曲线，肘部法则会说 “我们来看这个图，在 K = 3的位置看起来是一个很清楚的肘点” 对吧。这就类比于人的手臂，K = 3就是肘关节，我们的手就在右边这里：

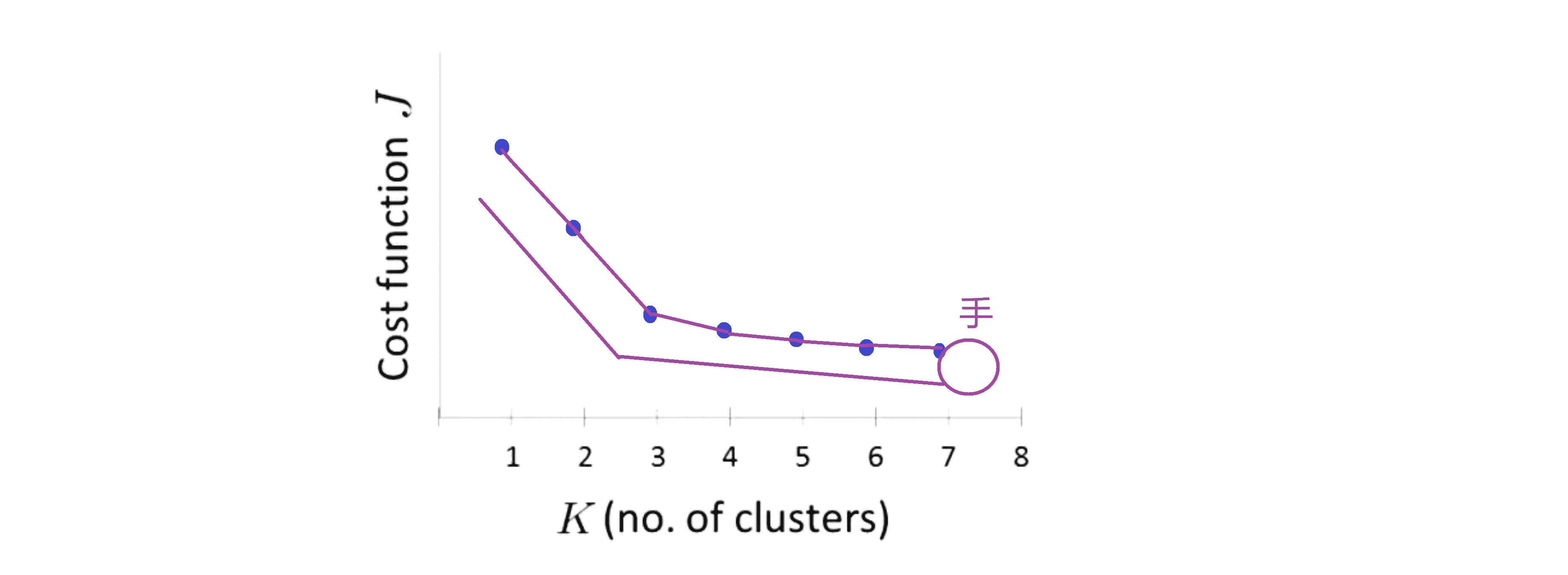
这就是肘部法则。你会发现这样一种模式，K从1变化到2 再从2到3时代价迅速下降，然后在3的时候到达一个肘点后， 此后代价值就下降得非常慢。这样看起来也许使用3个类是聚类数目的正确选择，这是因为那个点是曲线的肘点。如果我们得到了一个像上面那样的图，那么这非常好的。

而事实证明肘部法则并不那么常用，其中一个原因是如果你把这种方法用到一个聚类问题上，事实上你最后得到的曲线通常看起来是更加模棱两可的，也许就像下图这样：

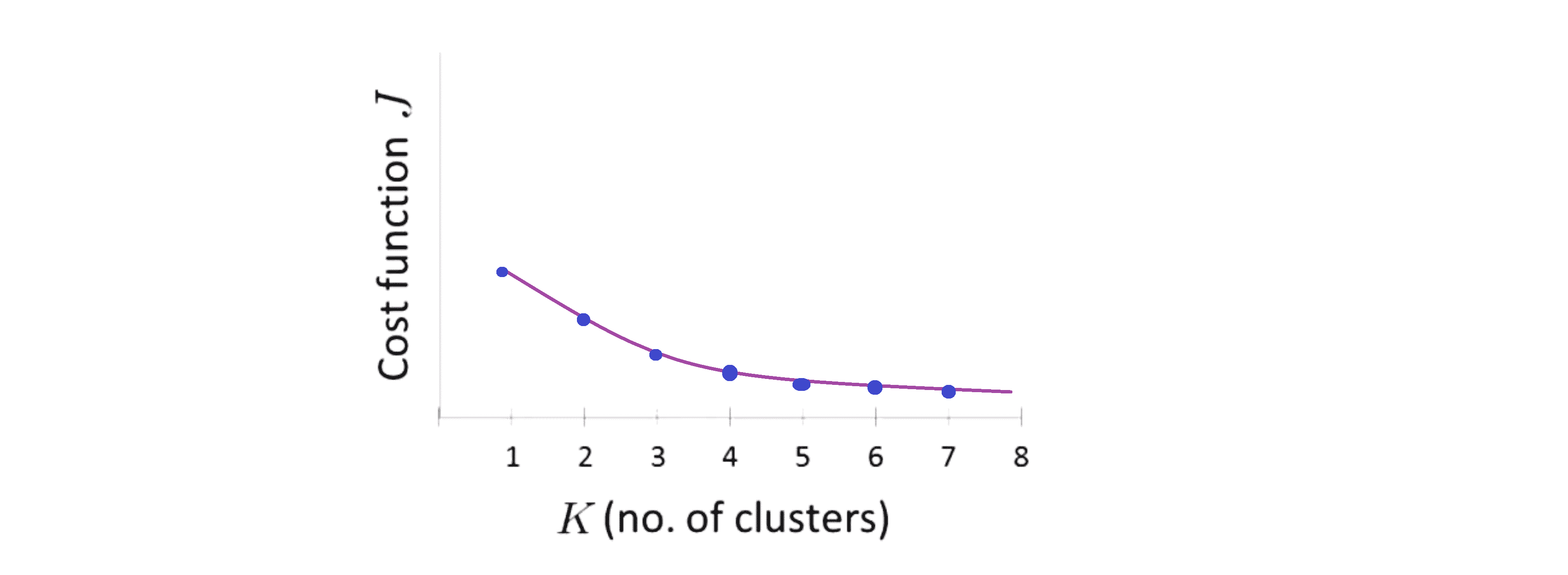
如果你看这条曲线也许没有一个清晰的肘点，而代价值像是连续下降的，也许3是一个好选择吗，也许4是一个好选择，也许5也不差……在这种情况下肘部法则就发挥不了它的作用了。

简单小结一下肘部法则，它是一个值得尝试的方法，但是我们不要过度期待它在任何问题上都有很高的表现。

最后有另外一种方法来考虑如何选择K的值。通常人们使用 K-均值聚类算法是为了某些后面的用途或者说某种下游的目的而要求得一些聚类。也许你会用K-Means算法来做市场分割，比如我们之前谈论的T恤尺寸的例子等等，或者可能为了某些别的目的学习聚类等等，如果那个后续或者说下游的目的比如市场分割能给我们一个评估标准，那么通常来说决定聚类数量的更好的办法 看不同的聚类数量能为后续下游的目的提供多好的结果。

我们来看一个具体的例子，我们再看一下T恤尺寸这个例子：

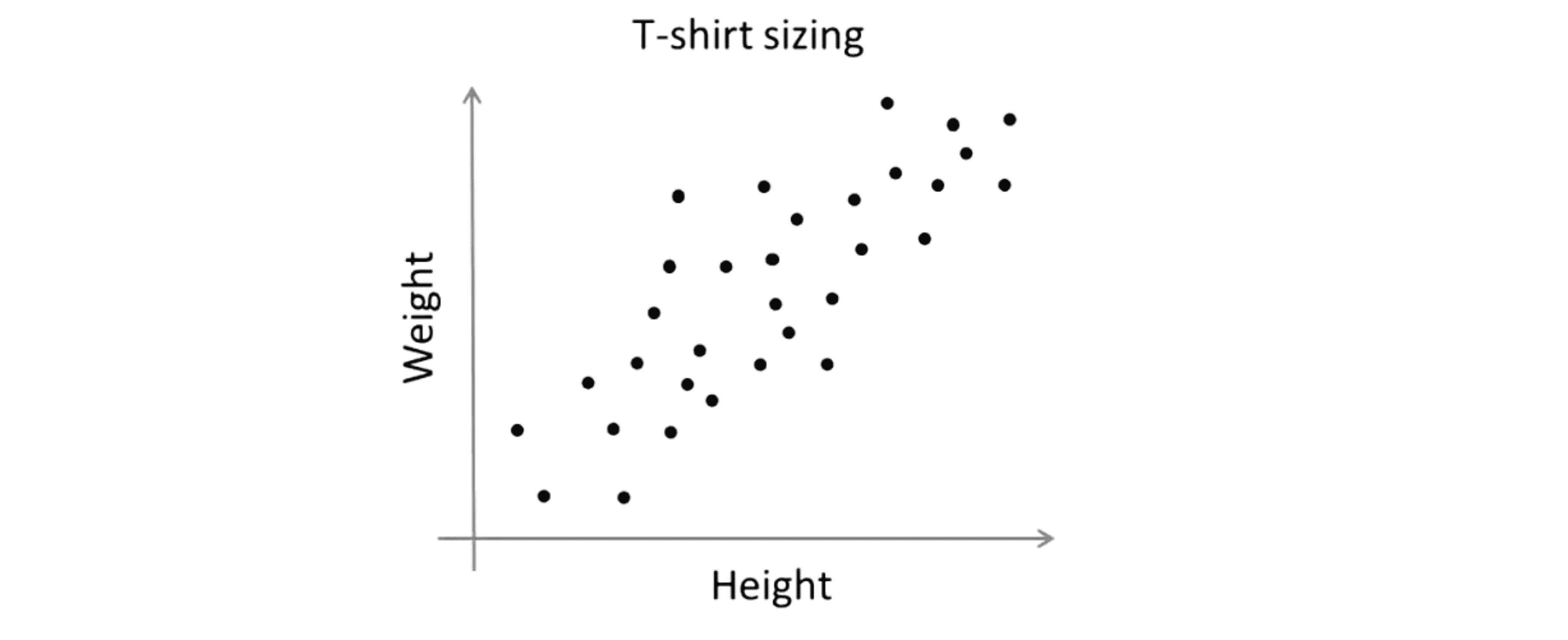
假如，我想要决定我是需要3种T恤尺寸，那我选择 K=3 我可能有小号 中号 大号三类T恤：

或者我可以选择 K=5 或者我可以选择需要5种T恤尺寸，此时 K=5 那么我可能有 特小号 小号 中号 大号 和特大号尺寸的T恤：

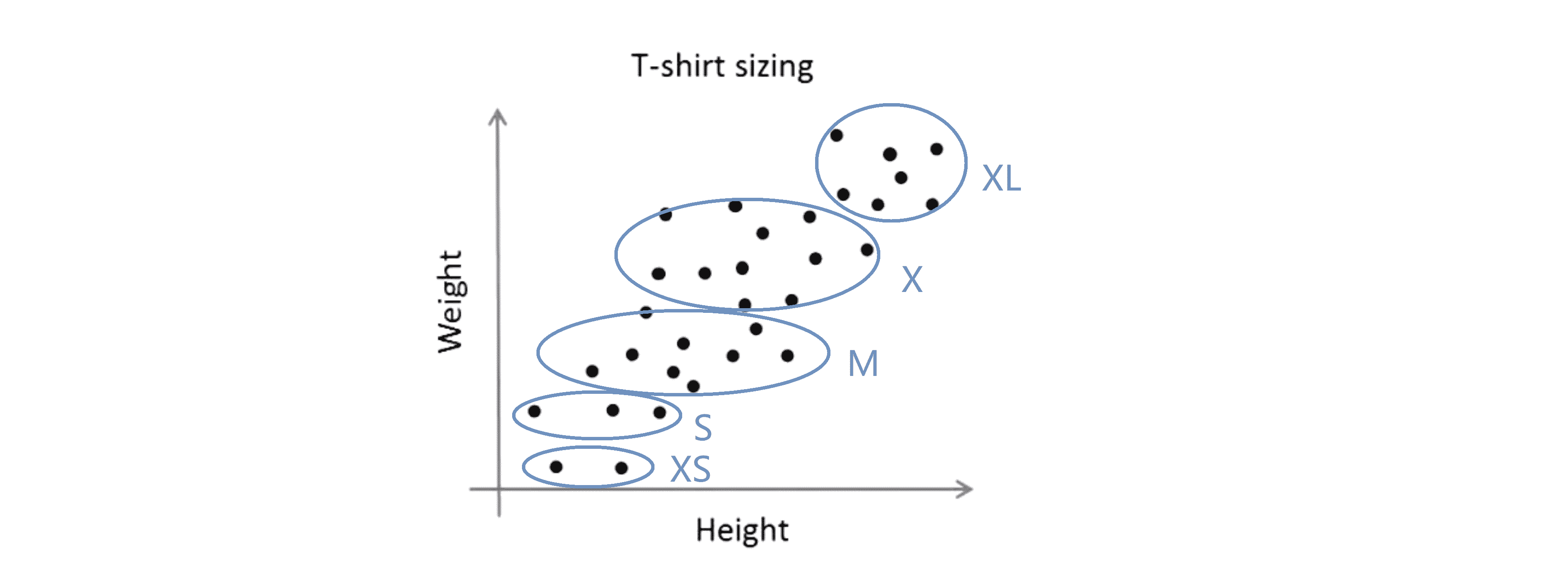
这个例子的好处是它会给我们选择聚类数目是 3 还是 5 的另一种方法。具体来说我们要做的是从T恤生意的角度来思考这个事情，然后问 “如果我有5个分段，那么我的T恤有多适合我的顾客？我可以卖出多少T恤？我的顾客将会有多高兴呢？” 从T恤生意的角度去考虑其中真正有意义的是 也就是我是需要更多的T恤尺寸来更好地满足我的顾客还是说我需要更少的T恤尺寸，但是我制造的T恤尺码就更少我就可以将它们更便宜地卖给顾客。因此T恤的销售业务的观点可能会提供给你一个决定采用3个类还是5个类的方法。

以上就是一个后续下游目的决定 K 的一个例子。

总结一下大部分时候聚类数目仍然是通过手动人工输入或我们的洞察力来决定；一种可以尝试的方法是使用肘部法则，但是我们不会总是期望它能表现得好；我想选择聚类数目的更好方法是去问一下自己运行K-Means算法是为了什么目的？然后想一想聚类的数目是多少才适合你运行K-Means算法的后续目的。

实现代码

思路在上面已经很清楚的介绍了，下面给我自己用CPP实现的二维K-Means算法代码，供大家交流学习：

#include <ctime> 
#include <cmath>
#include <cstdio> 
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
double testx[1100], testy[1100];//训练集点的下标 
double centrex[1100], centrey[1100];//聚类中心坐标 
int color[1100];//训练集点对应的颜色
int ans_color[1100];//记录答案颜色 
int num[1100];//记录每个聚类有多少个点 
double ans_J = -1, J;//记录最优的代价函数和现在的代价函数 
int K, m;

void read() {
    printf("请输入聚类数量K:");
    scanf("%d", &K);

    printf("请输入样本数量m:");
    scanf("%d", &m);

    printf("请输入m行，每行一个坐标x和y代表一个训练样本：\n");
    for(int i = 1; i <= m; i++) {
        scanf("%lf%lf", &testx[i], &testy[i]);
    }

    return; 
} 

double calc_dis(int x, int y) {
    double ans = 0;
    ans = (testx[x] - centrex[y]) * (testx[x] - centrex[y]) + (testy[x] - centrey[y]) * (testy[x] - centrey[y]);
    return(ans);
}

void K_Means() {
    int visit[1100];//标记第i个点是否已经作为中心 
    for(int o = 1; o <= 100; o++) {
        memset(visit, 0, sizeof(visit));
        memset(color, 0, sizeof(color));

        for(int i = 1; i <= K; i++) {
            int k = rand() % m + 1;
            while(visit[k]) k = rand() % m + 1;

            visit[k] = 1; 
            centrex[i] = testx[k];
            centrey[i] = testy[k];
        }//初始化聚类中心 

        int flag = 1;
        while(flag) {
            flag = 0;
            memset(num, 0, sizeof(num));
            for(int i = 1; i <= m; i++) {
                int now_color = 1;
                double min_dis = calc_dis(i, 1);

                for(int j = 2; j <= K; j++) {
                    double dis = calc_dis(i, j);
                    if(dis < min_dis) {
                        now_color = j;
                        min_dis = dis;
                    }
                }

                if(now_color != color[i]) {
                    flag = 1;
                    color[i] = now_color;
                }
            }//将点染色成离他最近的聚类的样子 

            memset(centrex, 0, sizeof(centrex));
            memset(centrey, 0, sizeof(centrey));
            for(int i = 1; i <= m; i++) {
                num[color[i]]++;
                centrex[color[i]] += testx[i];
                centrey[color[i]] += testy[i];
            }

            for(int i = 1; i <= K; i++) {
                if(!num[i]) {
                    int k = rand() % m + 1;
                    centrex[i] = testx[k];
                    centrey[i] = testy[k];
                }
                else {
                    centrex[i] = centrex[i] / (double)num[i];
                    centrey[i] = centrey[i] / (double)num[i];
                }
            }
        }

        J = 0;
        for(int i = 1; i <= m; i++) {
            J = J + calc_dis(i, color[i]);
        }

        if(ans_J == -1 || J < ans_J) {
            ans_J = J;
            for(int i = 1; i <= m; i++) {
                ans_color[i] = color[i];
            }
        }

    }

    return ;
}

void print() {
    for(int i = 1; i <= m; i++) {
        printf("第%d个点属于第%d簇\n", i, ans_color[i]);
    }

    return;
}
void work() {
    srand(int(time(0)));
    read();
    K_Means();
    print();
}
int main() {
    work();
    return 0;
}

结语

通过这篇BLOG，相信你已经对K-Means算法有所掌握。这时我们一同学习的第一个无监督学习算法，在之后的BLOG里，我们还会一同学习更多更强大的算法。最后希望你喜欢这篇BLOG！