今天在训练的时候，我在做题打表的时候意外发现我们的三角函数和710这个数字有着千丝万缕的不解之缘。查阅资料无果后经过推导我发现了背后的奥妙。今天就让我们来看看关于三角函数和710的那些事吧。

先从一道题目开始

这是ICPC 2019-2020 North-Western Russia Regional Contest的B题，题目大意如下：

Treap是一种在二叉搜索树中存储一组结构体的数据结构。树的每个节点都是一对包含（x，y）的结构体。

节点的 x 值是存储的是数据的 key 值。在Treap中，x 值遵循“二叉搜索树规则”：即对于任意一个节点，节点的左子树中的所有 x 值小于其 x 值，节点右子树中的所有 x 值大于其 x 值。

节点的 y 值遵循“堆规则”：即对于任意节点，节点的 y 值小于或等于其父节点的 y 值。一般来说 y 值都是直接随机出来的.Treap的结构如下图：

SJ1.png

现在我们规定，对于给定的 key 值也就是 x 值，其节点的 y 值为 y = sin x

给定你n（n ≤ 5e4），让你输出 n 个整数的 x 值（在int范围内），使得这棵Treap呈现链状。

这题乍一看好像是神仙题，但仔细一想在什么情况下我们的Treap会轻而易举的形成链状呢？显然如果当我们把我们n个x 值排序后，如果我们的 y 值也具有单调性，那么我们的Treap一定呈现链状，如果我们假设a1 < a2 < …… < an，那么我们就有：

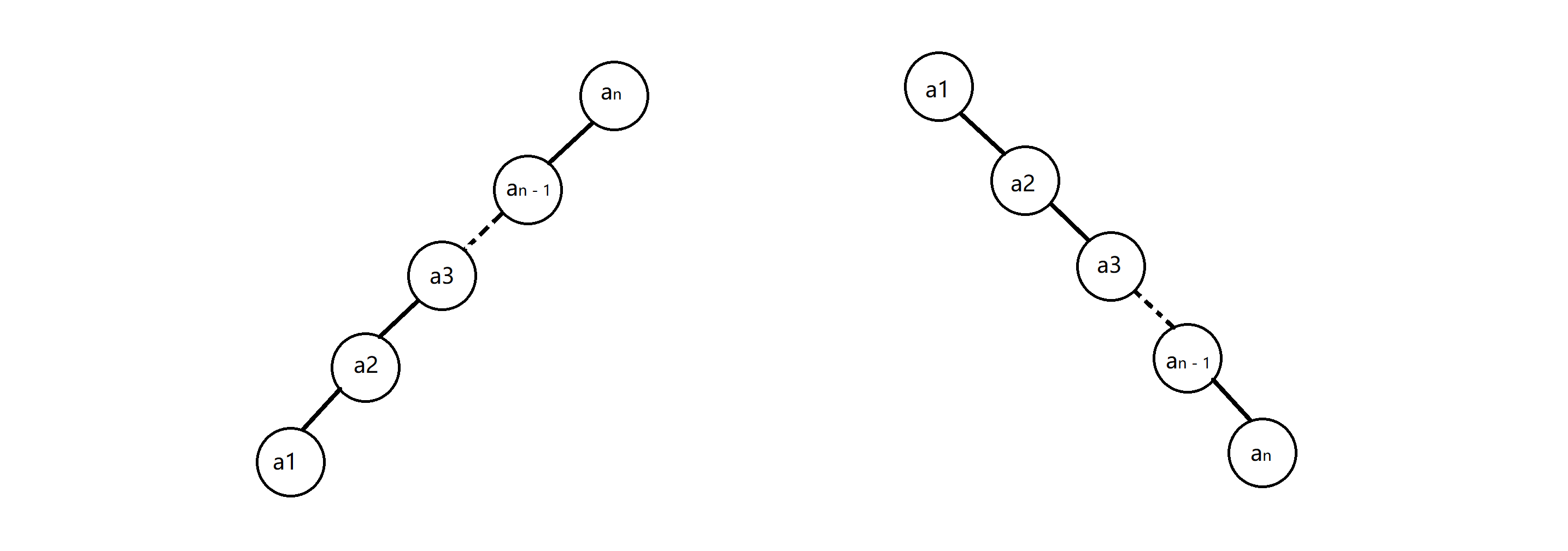
SJ2.png

如上图，当 x 单调递增时， y 也单调递增时，我们就会得到左边这条链；而当 x 单调递增时， y 单调递减时，我们这会得到有边这条链。

那我们如何构造出 n 个int范围内的整数x[i]，使他们从小到大排列后sin(x[i])也具有单调性呢？毫无头绪的情况下我重拾旧业，开始打表：

既然sinx是关于原点对称的，所以我就假定在y轴左边找到n/2个，在y轴右边找到n/2个，再加上原点就完美实现了。但是一个一个数枚举还是不现实，所以我们假设最后得到的答案的任意相邻两数的间隔是一定的，最后决定在1000以内枚举间隔。接着我打了下面这样一个表：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
long long num, n, flag;
double ans[22000];
int main() {
    n = 1000;
    num = 0;
    for(int i = 1; i <= 10000; i++) { //寻找间隔 
        flag = 0;
        for(long long j = 1; j <= n; j++) {
            ans[j] =  sin((long long)i * j - n * i / 2);//关于y轴对称 
            if(j >= 3) {
                if(ans[j] > ans[j - 1] && ans[j - 1] < ans[j - 2]){
                    flag = 1;
                    break;
                }
                if(ans[j] < ans[j - 1] && ans[j - 1] > ans[j - 2]){
                    flag = 1;
                    break;
                }
            }//判断单调性 
        }
        if(!flag) printf("%d\n", i);//如果具有单调性 
    }

    return 0;
}

输出结果710，没错今天的主角登场了：

SJ3.png

接着我就提交了酱紫一个程序：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
long long num, n;
int main() {
    scanf("%lld", &n);
    num = 0;
    for(long long i = 1; i <= n; i++) printf("%lld\n", (long long)710 * i - (long long)710 * (long long)n/ (long long) 2);//关于y轴对称 
    return 0;
}

就直接AC了……接着报着好奇的心理，我输出了n = 20时的情况：

SJ4.png

现在可能还看不出什么，我再输出他对应的正弦值：

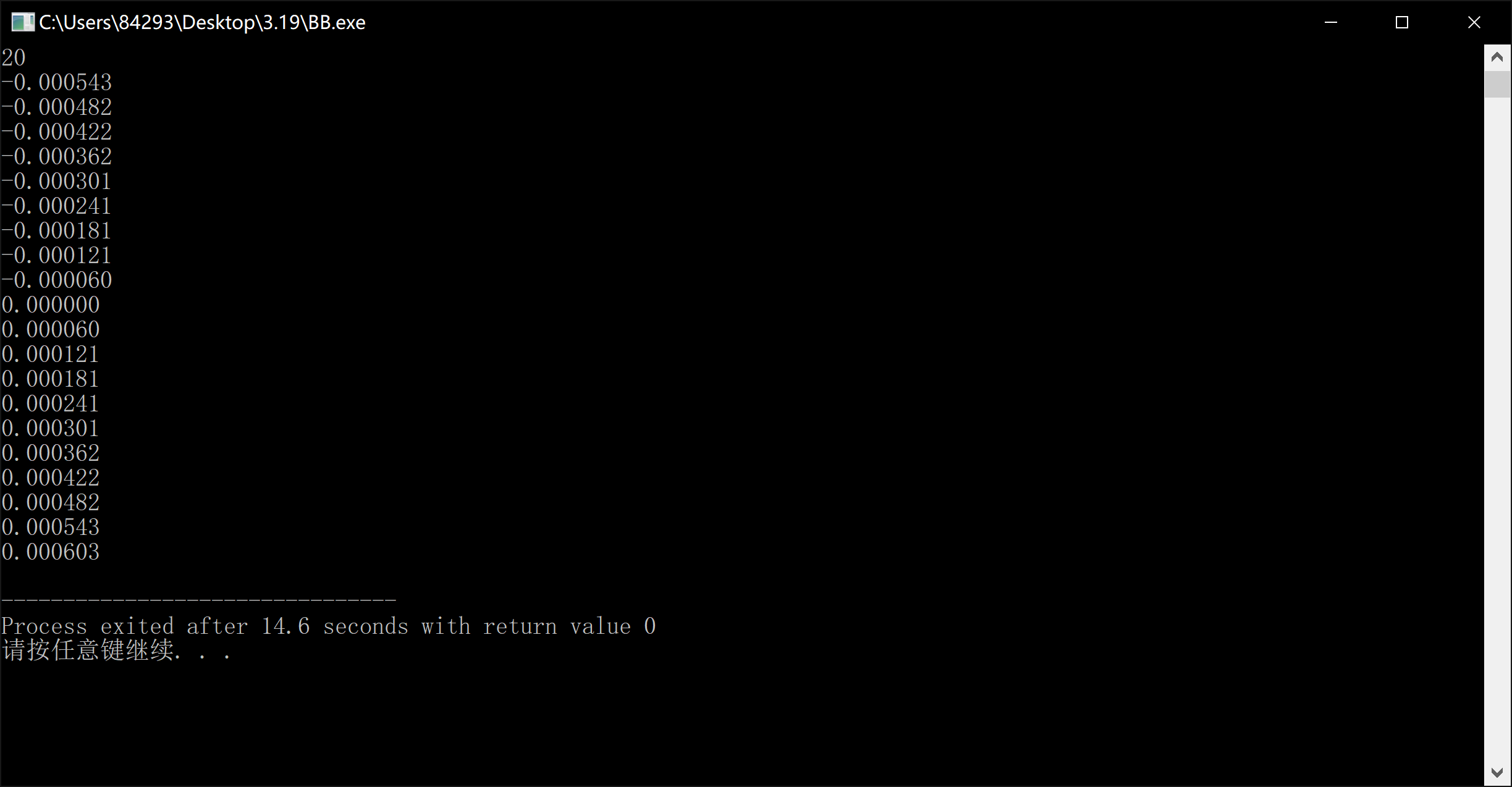
SJ5.png

可见它生成了较为密集且具有单调递增性质的sin值。可能这还看不出来，我们看一下50000的：

SJ6.png

可见生成的sin值基本涵盖[-1, 1]且相当密集。

换言之，对于x是整数的情况，sin(710 * x)可以生成密集的具有单调性的正弦函数。这就非常有意思了啊：

SJ7.png

我们的sin（710 * x）的图像难道会是上图这样的吗？

只有710吗

在好奇心的驱使下我开始探究，如果对于整数 x ，当x递增时，想让 sin(c * x) 也具有单调性，那么 c 一定要是 710 吗？

所以我把之前的打表程序的范围进行了修改，把搜索范围扩大到了一万：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
long long num, n, flag;
double ans[22000];
int main() {
    n = 1000;
    num = 0;
    for(int i = 1; i <= 10000; i++) { //寻找间隔 
    //间隔的搜寻范围扩大到10000 
        flag = 0;
        for(long long j = 1; j <= n; j++) {
            ans[j] =  sin((long long)i * j - n * i / 2);//关于y轴对称 
            if(j >= 3) {
                if(ans[j] > ans[j - 1] && ans[j - 1] < ans[j - 2]){
                    flag = 1;
                    break;
                }
                if(ans[j] < ans[j - 1] && ans[j - 1] > ans[j - 2]){
                    flag = 1;
                    break;
                }
            }//判断单调性 
        }
        if(!flag) printf("%d\n", i);//如果具有单调性 
    }

    return 0;
}

一看输出结果，哟 710 的倍数一家都来了呢：

SJ8.png

换言之只要是710的倍数都具有类似的性质。那么为什么是710呢？

为什么是710

我苦苦搜寻了一大圈的资料，但却无果。没办法只好自己手动去推导了。

首先第一个问题是，既然710的倍数可以，那它的一半355为什么不可以呢？

我修改了一下之前的提交程序：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
long long num, n;
int main() {
    scanf("%lld", &n);
    num = 0;
    for(long long i = 1; i <= n; i++) printf("%lf\n", sin((long long)355 * i - (long long)355 * (long long)n / (long long) 2));
    return 0;
}

输出结果我们发现：

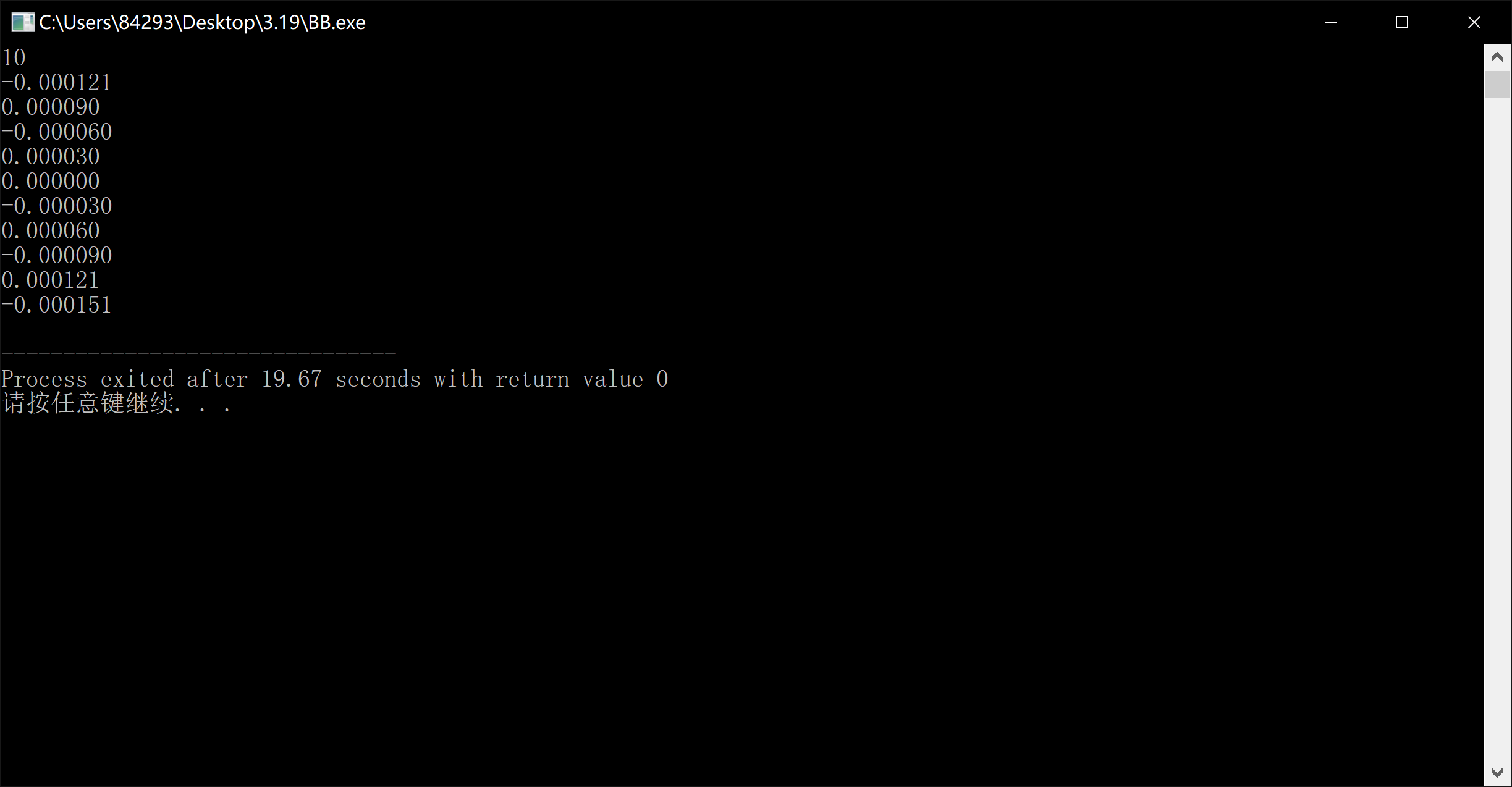
SJ9.png

但看绝对值还是和刚刚一样都是先下降再上升，但是这次1符号却不是0的左边全是负号，右边全是正号，而是正号负号交叉进行。那可能是什么原因呢？

“周期性”，对于sinx，如果让他变化一个很小的数 λ ，并且加上一些周期我们就会发现 sin(x + λ) = sin(x + λ + 2Π) = -sin(x + λ + Π)

换言之，加上半个周期，符号就会改变，再加上半个周期，其符号就会变回来。是不是发现了什么？

没错我们可以把355看成是半个周期，而710就是一个周期，这样就解释的通为什么710的倍数也具有一样的性质。

接下来又回归到了最开始的问题，为什么是710？

接下来我试探性的打了下面这样一个程序，去寻找10000内距离距离它最近的Π的倍数最小的七个数和他们分别的距离：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
const double pi = asin(1) * 2;
double a[1100000];

double check(double x) {
    return(min(ceil(x) - x, x - floor(x)));
} 

int main() {
    int n = 10000;
    for(int i = 1; i <= n; i++) a[i] = check(i / pi);//寻找距离 
    sort(a + 1, a + n + 1);

    for(int o = 1; o <= 7; o++) {
        for(int i = 1; i <= n; i++) {
            if(check(i / pi) == a[o]) {
                printf("%d %lf\n", i, a[o]);
                break;
            }
        }
    }
    return 0;
}

最后发现果不其然，还是710那一家老小：

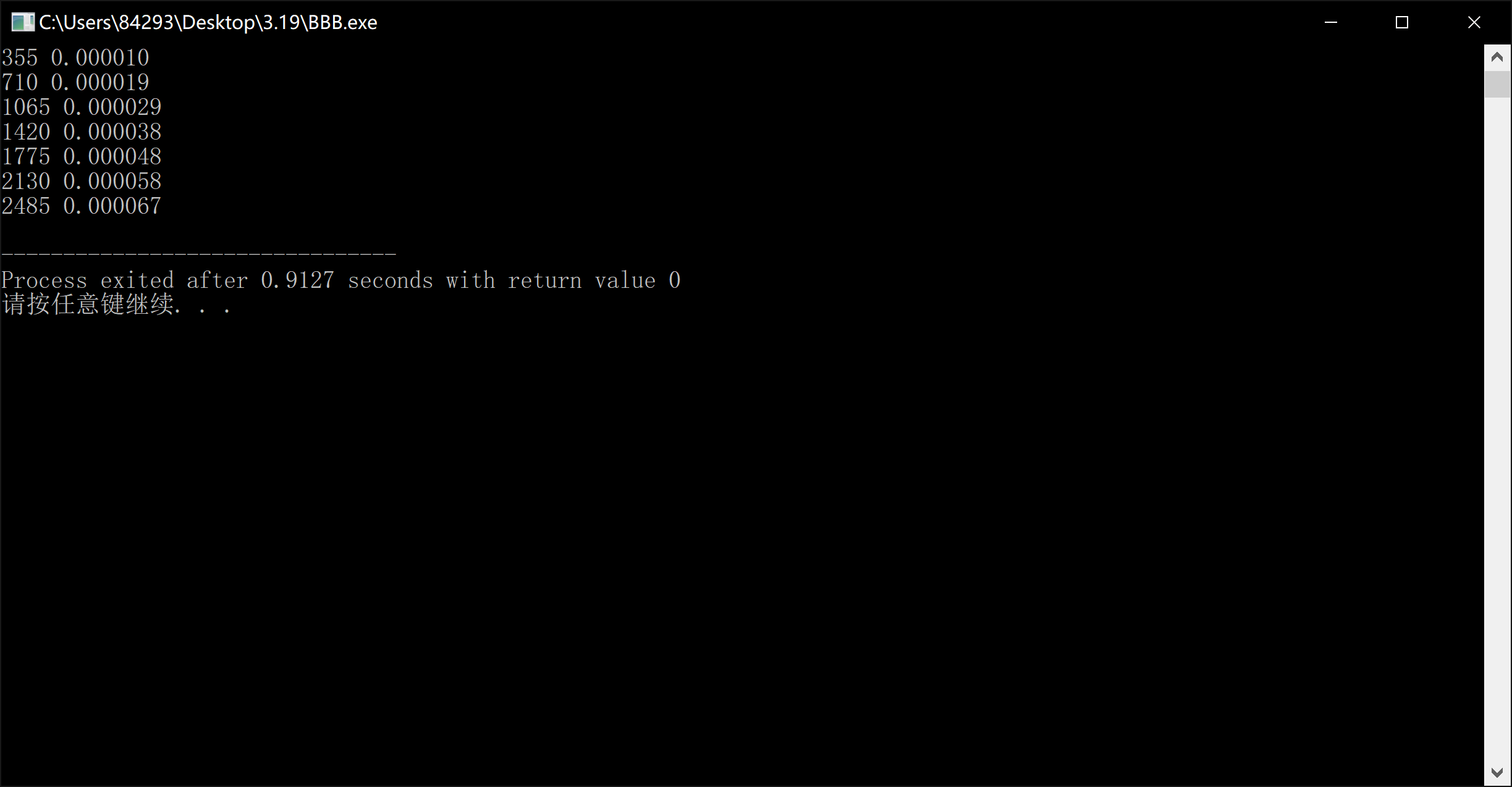
SJ10.png

那道理就很好解释了，710/Π≈226，误差在小数点后第五位，也就是说我们可以把710近似地看成226Π，那么如果是sin(c x) = sin(x 226Π)的话，那么sin这个结果会一直是0对吧。但是这个1e-5的误差虽然很小，但是依然存在，这个误差就提供了一丝偏移，每一次我们的sin 都在加上了226个周期后都朝着同一个方向偏移了很小很小的一点点，所以这就是我们能用sin(710 * x)在int范围内生成单调的sin值的原因。

所以我们真正的sin(710*x)的图像应该是这样：

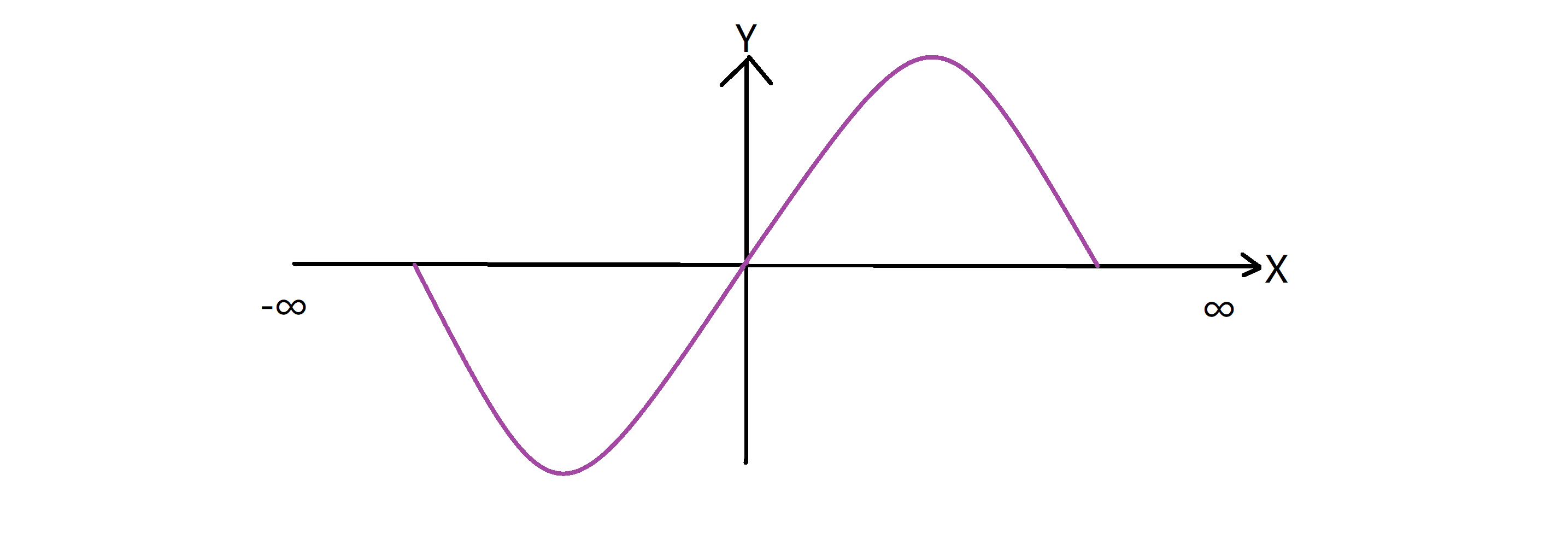
SJ7.5.png

其一个周期大概为1000000左右，换句话说如果题目数据范围再大，我们直接输出710的倍数就可能跨过单调区间，不输出的答案就一定是单调的了。

这也进一步解释了为什么sin(355 x)会出现一个正一个负的情况。其原因就是335 / Π = 113，是个奇数。所以即便是sin(x 113Π)，原本的符号就是+1,-1,+1,-1的，所以恰好出现了正负号交叉进行的情况。

到这里关于关于正弦函数和七百一十的那些事就基本梳理出来了。那只有710的倍数有这样的性质吗？当然不是，当我们的生成范围变成long long，搜索范围变成1000000时：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
const double pi = asin(1) * 2;
double a[1100000];

double check(double x) {
    return(min(ceil(x) - x, x - floor(x)));
} 

int main() {
    int n = 1000000;//扩大范围
    for(int i = 1; i <= n; i++) a[i] = check(i / pi);//寻找距离 
    sort(a + 1, a + n + 1);

    for(int o = 1; o <= 7; o++) {
        for(int i = 1; i <= n; i++) {
            if(check(i / pi) == a[o]) {
                printf("%d %lf\n", i, a[o]);
                break;
            }
        }
    }
    return 0;
}

我们就发现这次的主力军变成了10348一家老小：

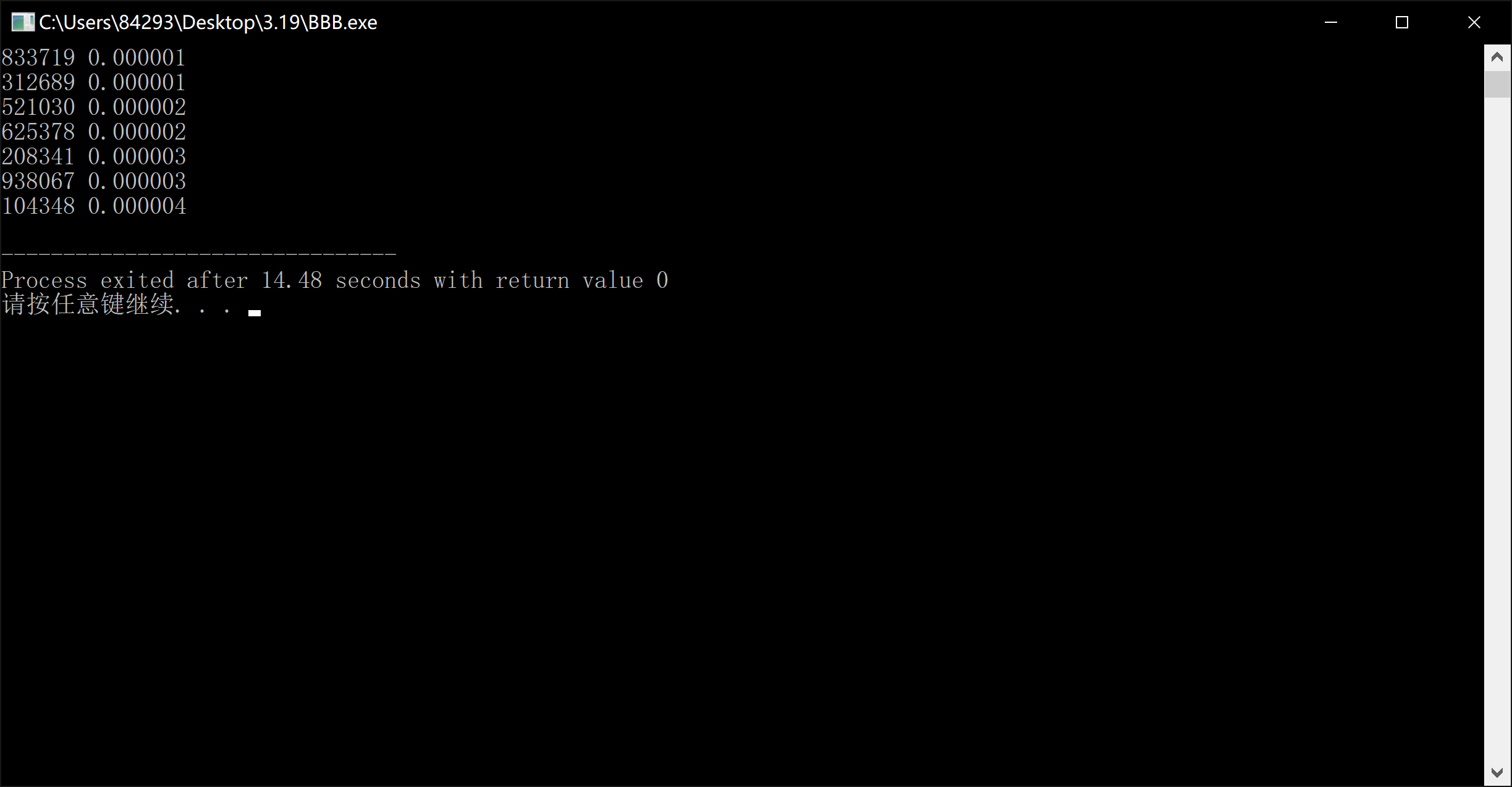
SJ11.png

它们与kΠ之间的差距达到了1e-6，也就是说用它们来当sin(c * x)中的c，可以生成出更加稠密的具有单调性的sin序列。更小的误差值带来的是更大的周期，这就解决了当 n 更大时，使用710构造输出序列的正弦值不是单调的问题。

那其他三角函数呢

那这次题目是x单调，要求正弦函数单调，那下次搞个余弦或者正切怎么办？没事我们一个一个搞定。

正切函数

首先是正切，正切是很好搞定的，因为在关于0对称的一个单调区间内，正切的单调性和正弦是基本相一致的，所以直接抄正弦的生成就好了：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
long long num, n;
int main() {
    scanf("%lld", &n);
    num = 0;
    for(long long i = 1; i <= n; i++) printf("%lld\n", (long long)710 * i - (long long)710 * (long long)n/ (long long) 2);//关于y轴对称 
    return 0;
}

此时若输出20个数对应的tan值：

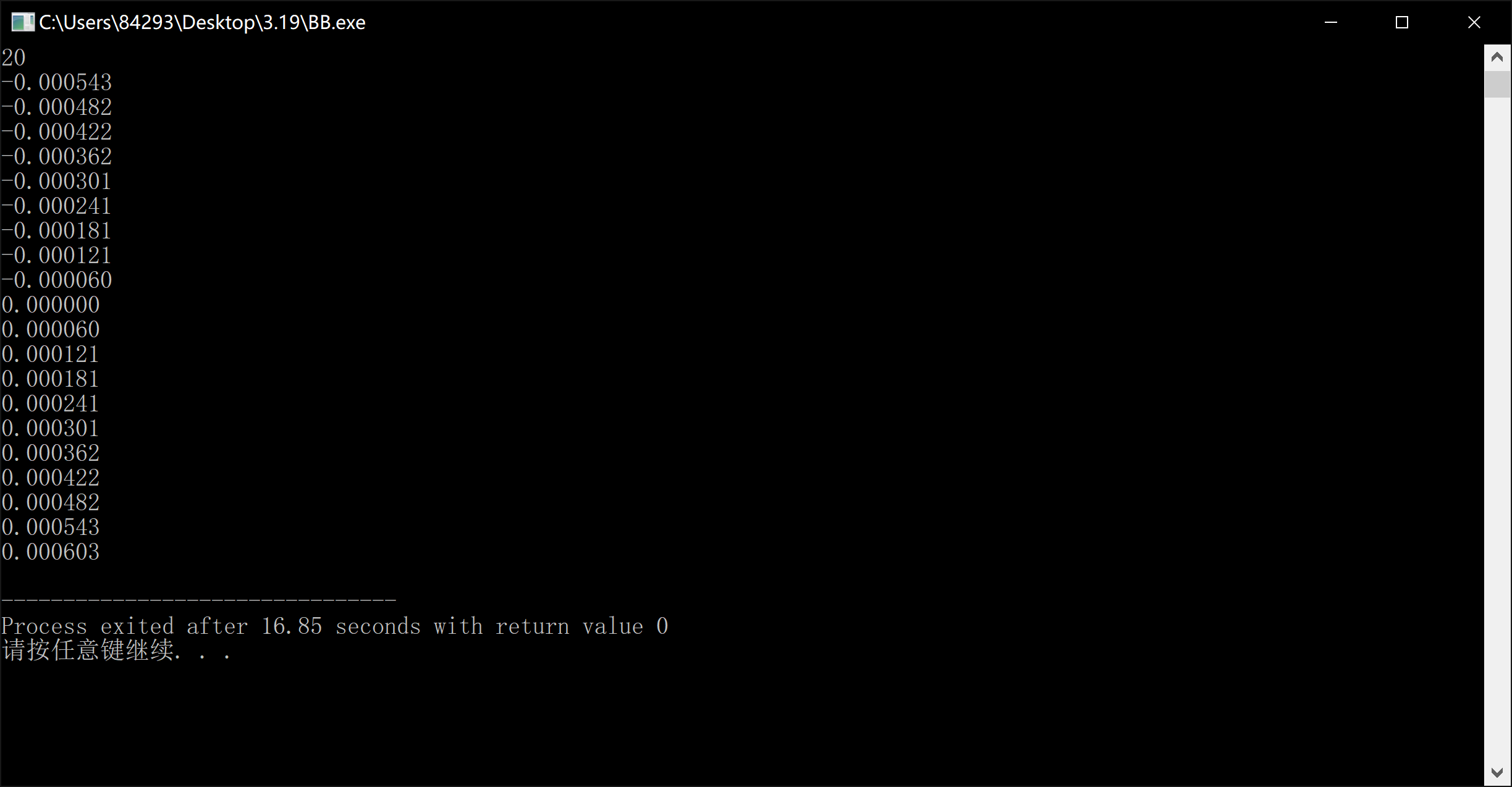
SJ12.png

就可以发现其和sin一样单调且密集。

余弦函数

余弦函数比较特殊，它的单调区间并不关于y轴对称，所以我们考虑只要y轴右半部分的单调区间即可：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
long long num, n;
int main() {
    scanf("%lld", &n);
    num = 0;
    for(long long i = 1; i <= n; i++) printf("%lld\n", (long long)710 * i);//只要y轴右半边 
    return 0;
}

此时若输出20个数对应的cos值，而由于开始时导数值较小，所以区间取到7100时才有比较明显的下降，可以在具体操作时可以视情况选择间距（在此输出以7100间距为例）：

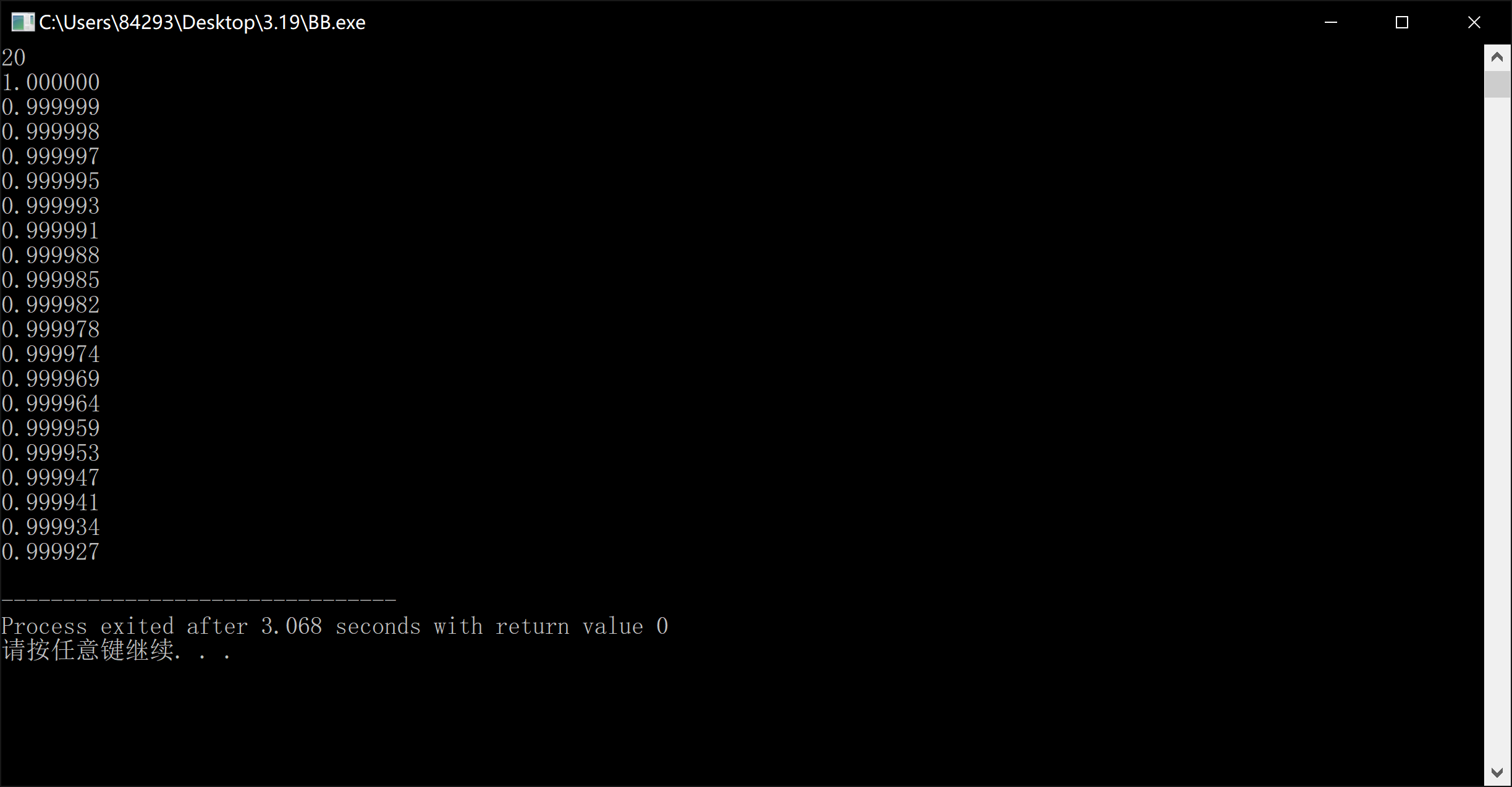
SJ13.png

就可以发现也是单调且密集。若想要随着x的递增单调递增的可以选取y轴的左半部分，这里就不赘述了。

结语

通过这篇BLOG，相信你已经完全了解了三角函数和七百一十的那些事，希望能在今后的学习生活中对你有所启发。最后希望你喜欢这篇BLOG！

Last modification：March 21st, 2020 at 12:17 am
© 允许规范转载
If you think my article is useful to you, please feel free to appreciate