终于到图论部分了，图论我是真心弱啊QwQ。今天复习了一下tarjan，总结了一下其基本用法，希望对你有帮助吧。

什么是tarjan？

tarjan算法又称“塔尖”算法，是解决图联通问题的一种神奇算法。换句话说，tarjan就是基于DFS算法，对每个点进行标记处理的一种基本图论算法。

tarjan有什么用？

由于tarjan是解决图联通的一种算法(:з」∠)，所以我们很自然的可以想到可以用来求强联通分量，割点，割边以及很经典的tarjan缩点。下面我们就一个一个来介绍这些经典的运用。这篇博客我们就先来求解强连通分量。

求强连通分量

强连通和强连通图

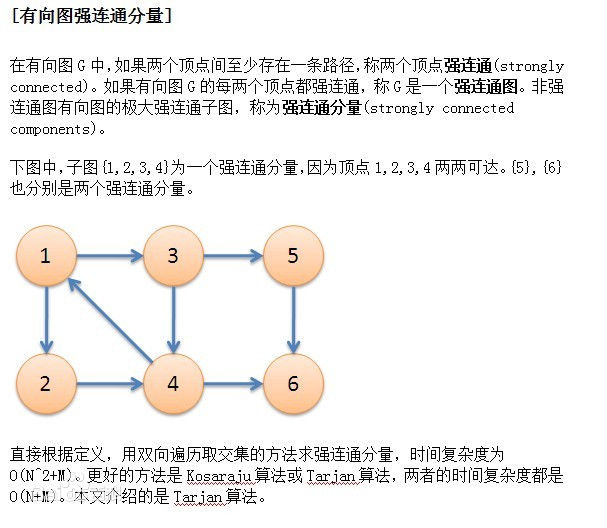
在一个有向图G里，设两个点x.y。若由x有一条路可以走到y，由y又有一条路可以走到x，我们就叫这两个顶点（x，y）强连通。

同理，如果 在一个有向图G中，任意两个点都强连通，我们就叫这个图，强连通图，特殊的，每一个单独的点都是一个强连通子图。

强联通分量

算法详解

首先我们要知道几个数组的含义：

struct node
{
    int x,y,next;
}a[110000];
int last[110000];
//数组a，last用前向星存储这幅图
int dfn[110000],low[110000],visit[110000],stack[110000],heads[110000];
//dfn【i】代表第i个点的搜索次序，也就是时间戳，换句话说，就是记录这个点是第几个被找到的，所以显然每个点的dfn都不一样。
//low【i】代表从这个点，可以到达时间戳最小的点。由于是这一幅图而不是一棵树，所以某个点的叶子节点可以是他的祖先，详细见下面的伪代码。
//visit数组和表面意思一样，就是记录某个点是否被访问过，若第i个点被访问，则visit【i】=1，反正为0.
//*stack数组顾名思义，是一个操作中栈，存储的是还没有确定归属于哪个强连通的点，是非常重要的数组，下文会详细讲解。
//head记录的是每个强连通分量的头结点（就是时间戳最小的那一个）。

我们来看看伪代码：

tarjan(u){

　　dfn[u]=low[u]=++Index 
  // 为节点u设定次序dfn【u】编号和low【u】初值，其中刚开始时，low【u】的值就为dfn【u】的值

　　Stack.push(u)   // 将节点u压入栈中

　　for each (u, v) in E // 枚举每一条边

　　　　if (v is not visted) // 如果节点v未被访问过

　　　　　　　　tarjan(v) // 继续向下找

　　　　　　　　Low[u] = min(Low[u], Low[v])

　　　　else if (v in S) // 如果节点u还在栈内

　　　　　　　　Low[u] = min(Low[u], LOW[v])
        //就是如果他的儿子节点是他的祖先，那么他最先能到达的点就是他这个祖先最先能到达的点。

　　if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根
    head[++]=u;// u号点为该强连通分量的头节点
　　repeat v = S.pop  // 将v退栈，为该强连通分量中一个顶点

　　print v

　　until (u== v)//当退栈推完u点，也就是这个强连通分量的头顶点时，就可以停止了。

}

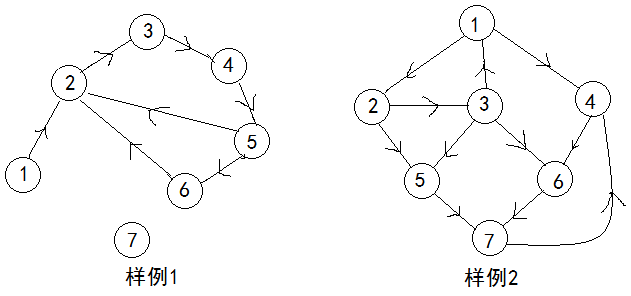
没看懂？没关系，下面我们就用一个很热门的图来讲解一下：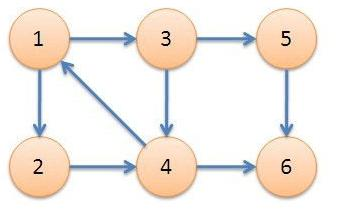
首先1号点入栈，时间戳为1；dfn[1]=low[1]=1;

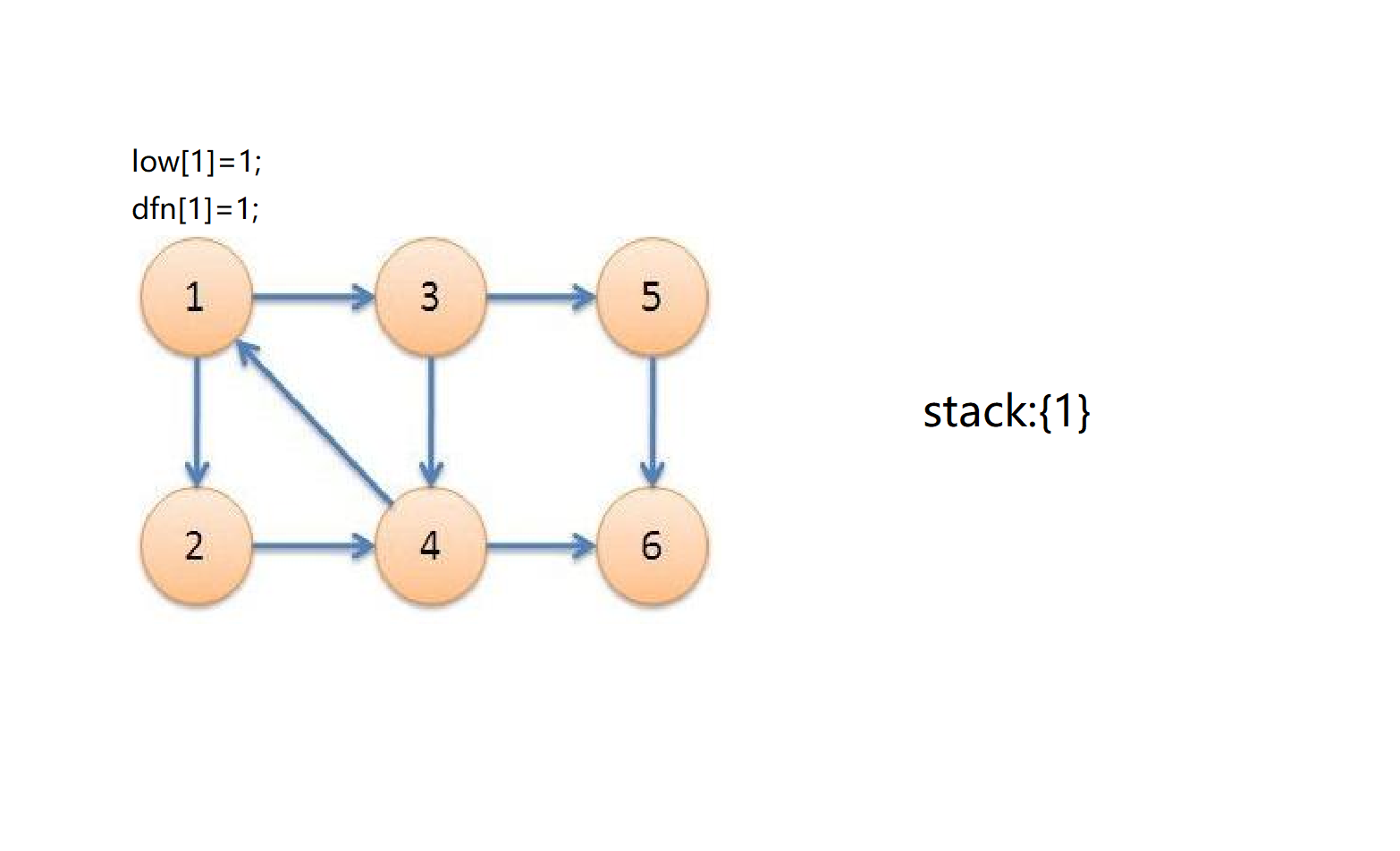
接着从1号点开始深搜，首先发现3号点，3号点入栈，时间戳为2，dfn[3]=low[3]=2;

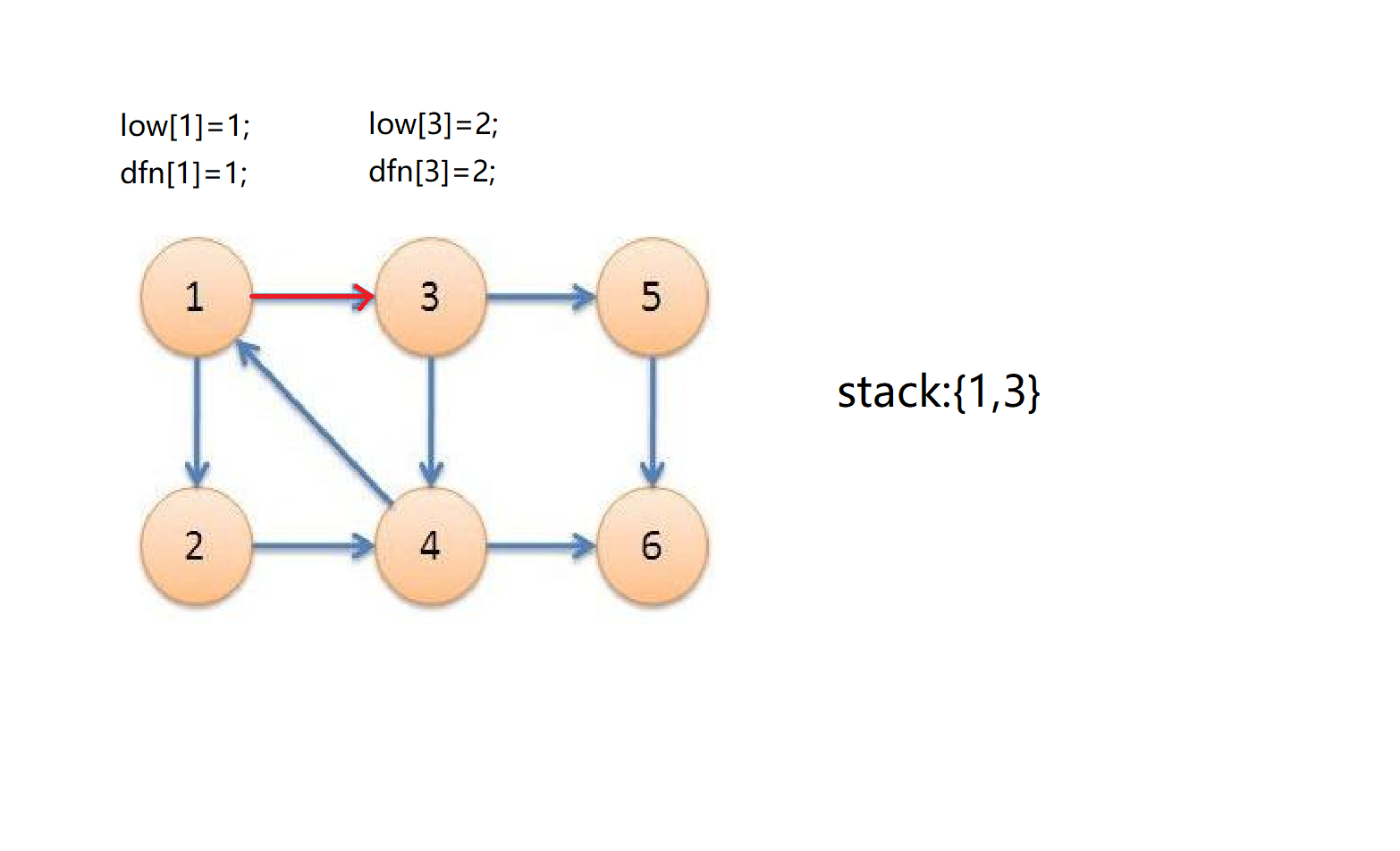
接着从3号点开始深搜，首先发现5号点，5号点入栈，时间戳为3，dfn[5]=low[5]=3；
;
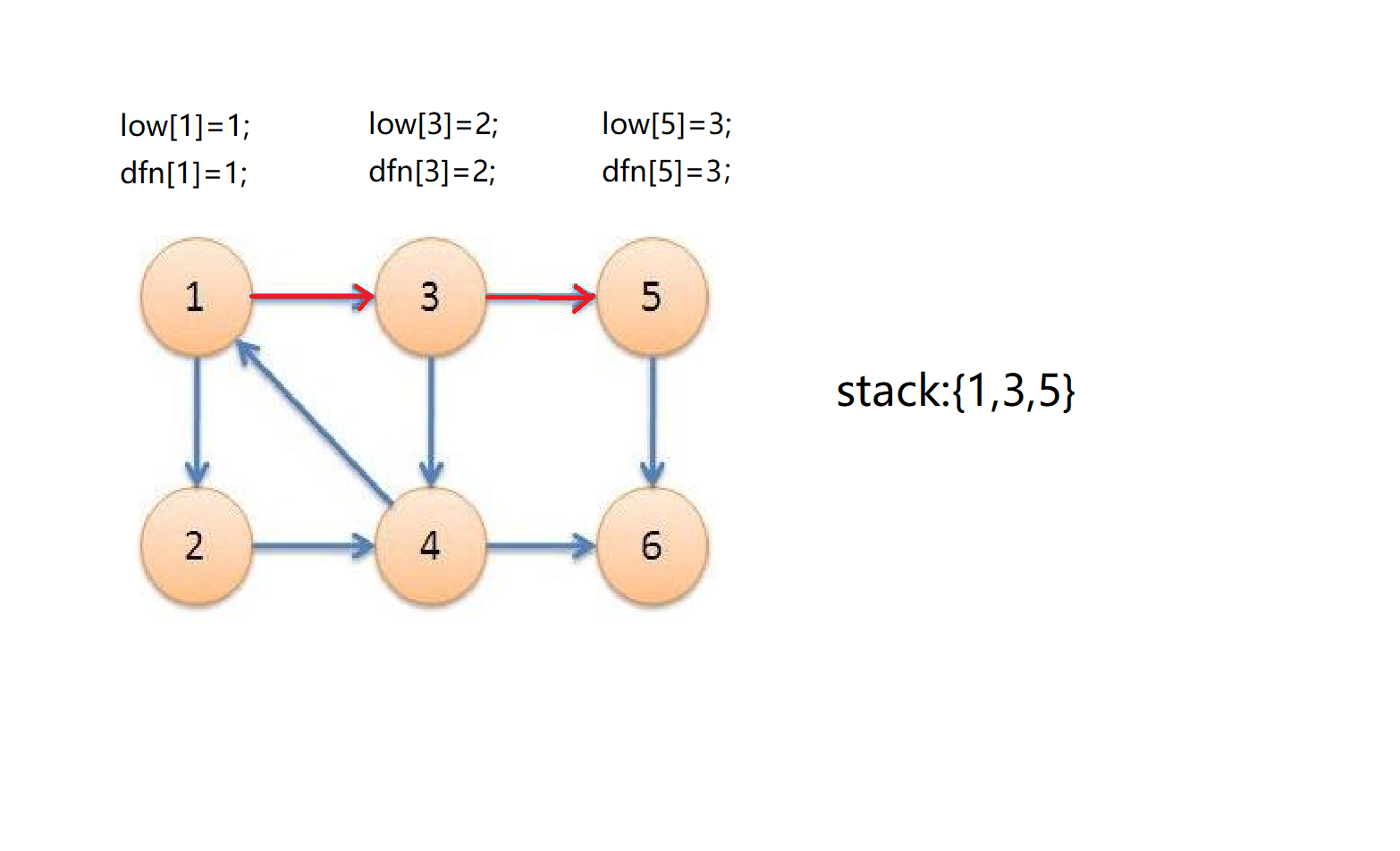同理接着从5号点开始深搜，发现6号点，6号点入栈，时间戳为4，dfn[6]=low[6]=4；

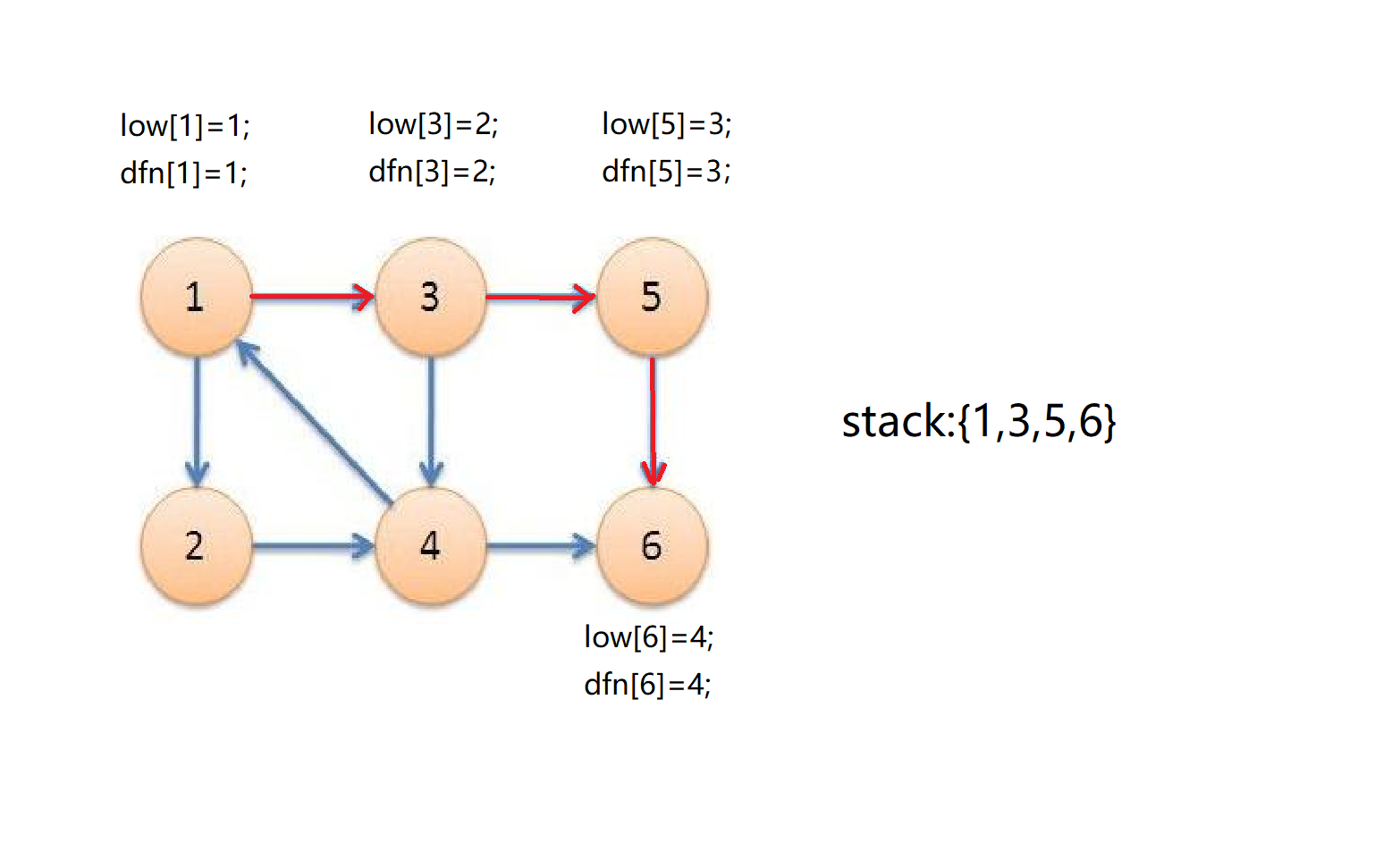
我们发现6号没有子节点，无法拓展，又发现dfn[6]==low[6]，所以我们已经找到了以6为头元素的第一个强连通分量。我们把栈中6及6后面所有的元素退栈（只有6），head中加一个6，它们（只有6）构成一个强连通分量。

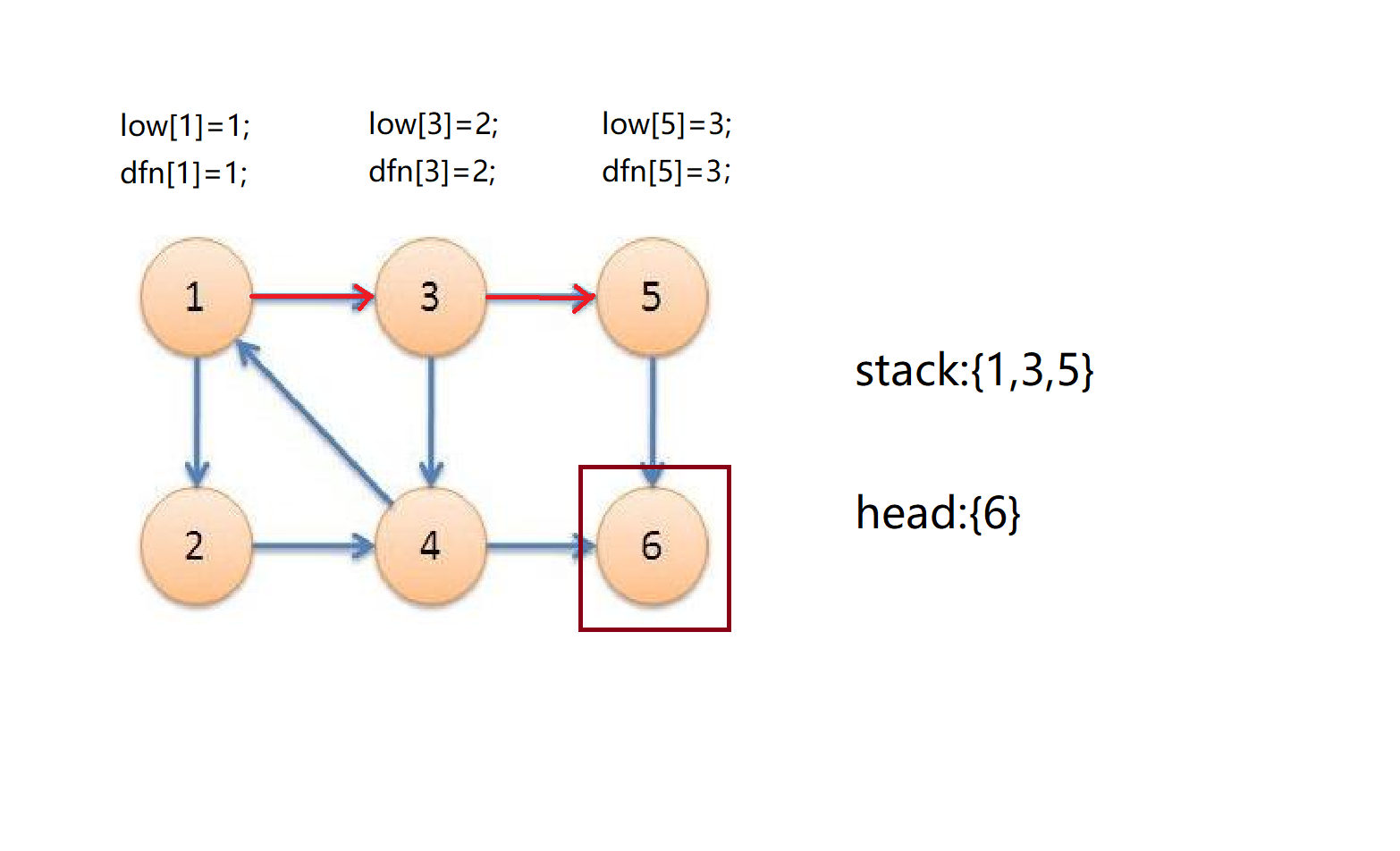
接着我们退回到5号节点，发现5号也没有其他子节点了，且dfn[5]==low[5]，所以我们已经找到了以5为头元素的又一个强连通分量。我们把栈中5和5后面所有的元素退栈（只有5），head中加一个5；

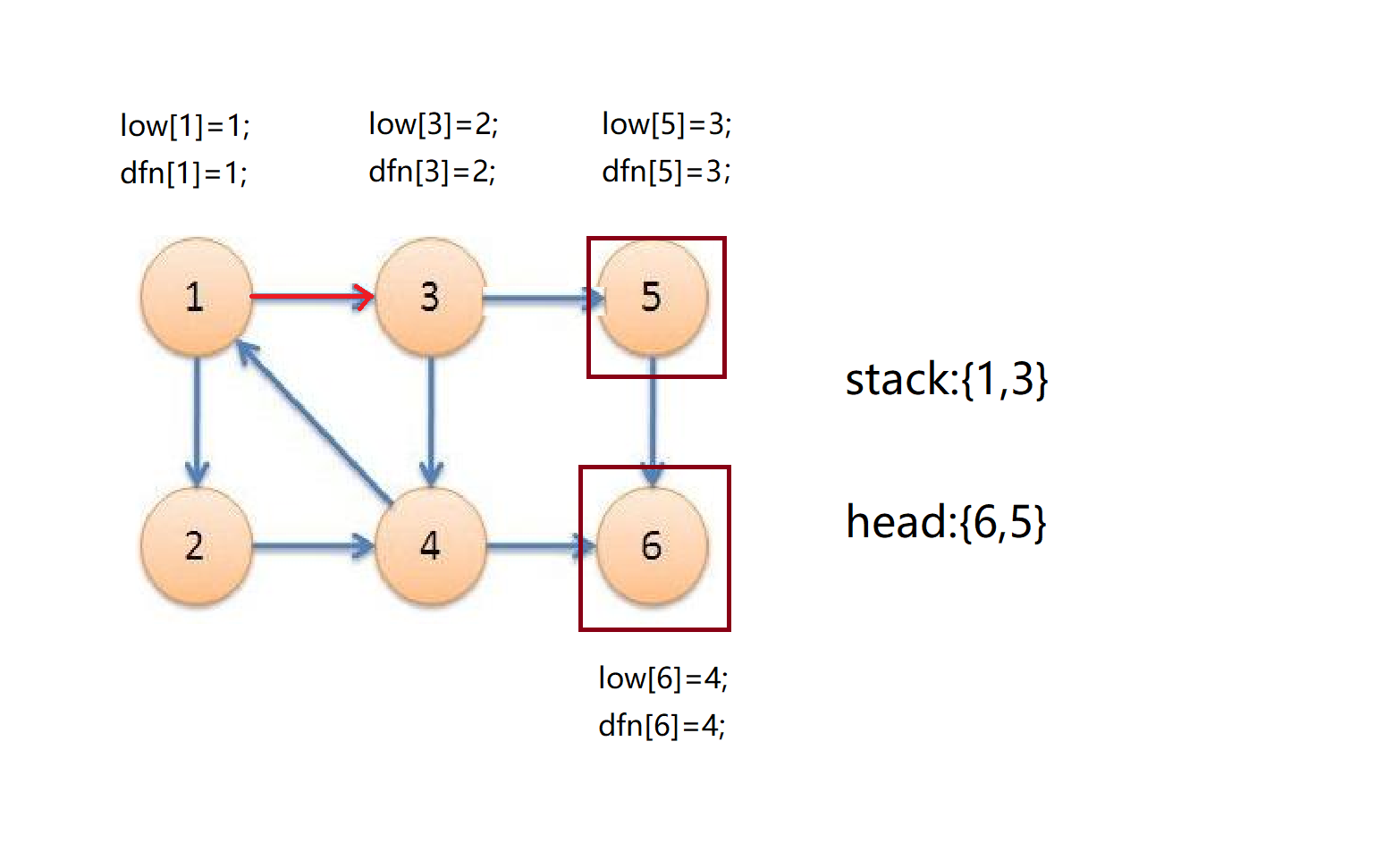
接着我们退回到3号节点，发现还有一个子节点4，4入栈，时间戳为5，dfn[4]=low[4]=5;

然后我们从4号点开始深搜，发现6号点，6号已经被访问过了且不在stack数组里，所以不用理他。接着我们发现4的另一个子节点1，1号点被访问过，且在stack里所以我们用low[1]来替换low[4];

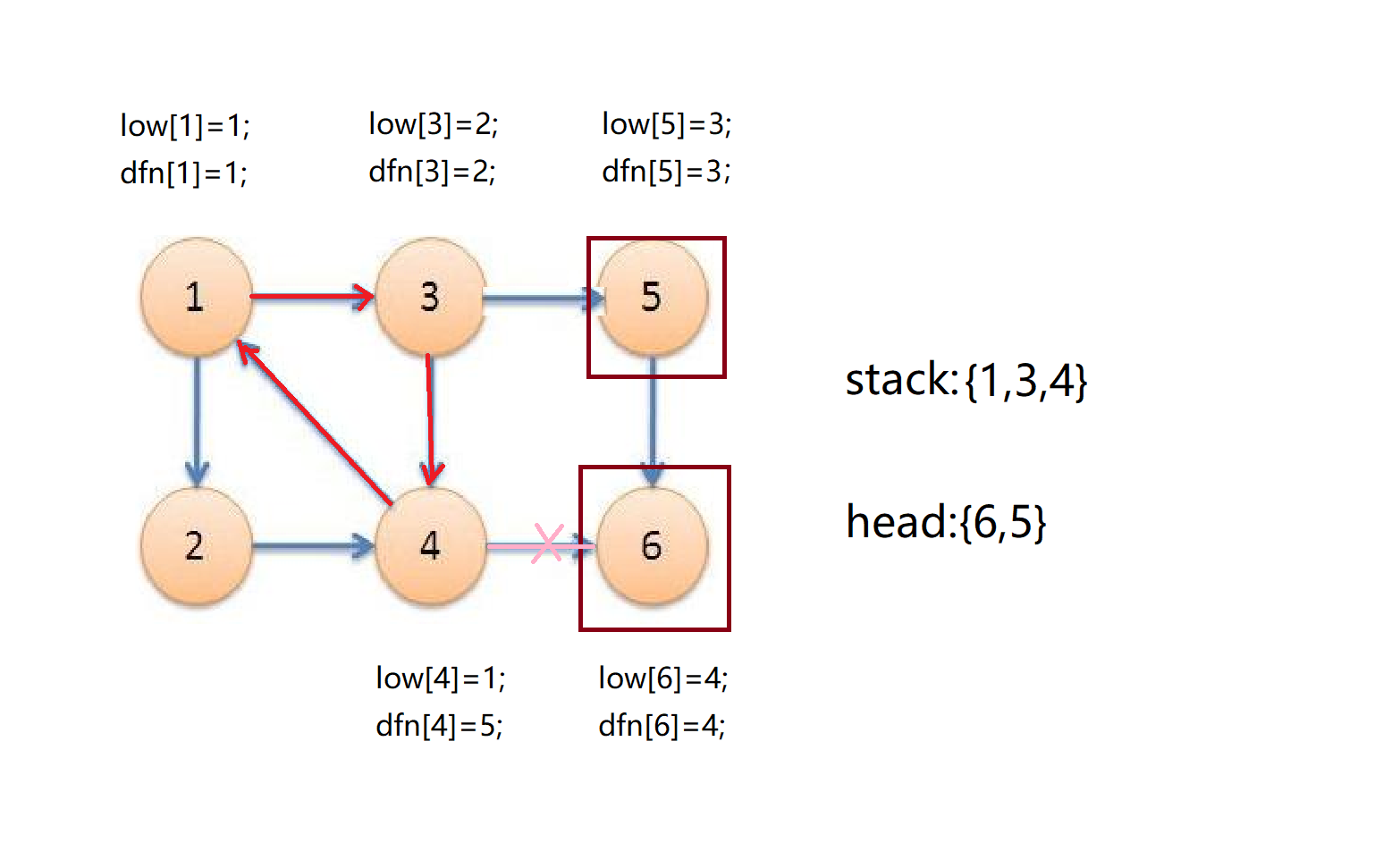
接着我们发现4号点已经没有子节点了，但是dfn[4]!=low[4],所以4号点不是某个强连通分量的头节点，我们直接退回3号点。我们发现low[4]小于low[3]所以用low[4]来替换low[3];

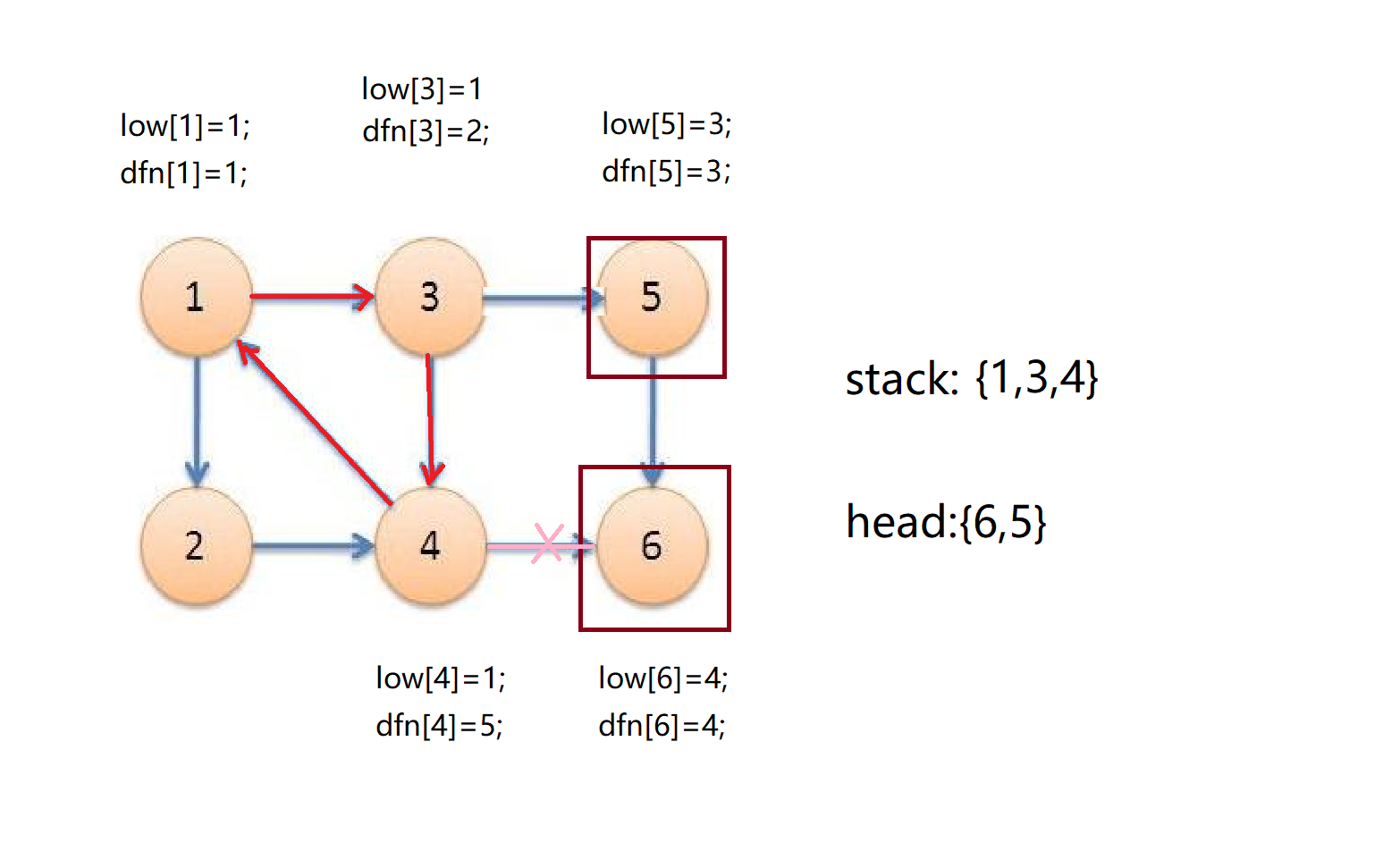
然后我们退回到1号点，发现1号点还有一个没有被发现过的儿子2，于是2入栈，时间戳为6，dfn[2]=low[2]=6;

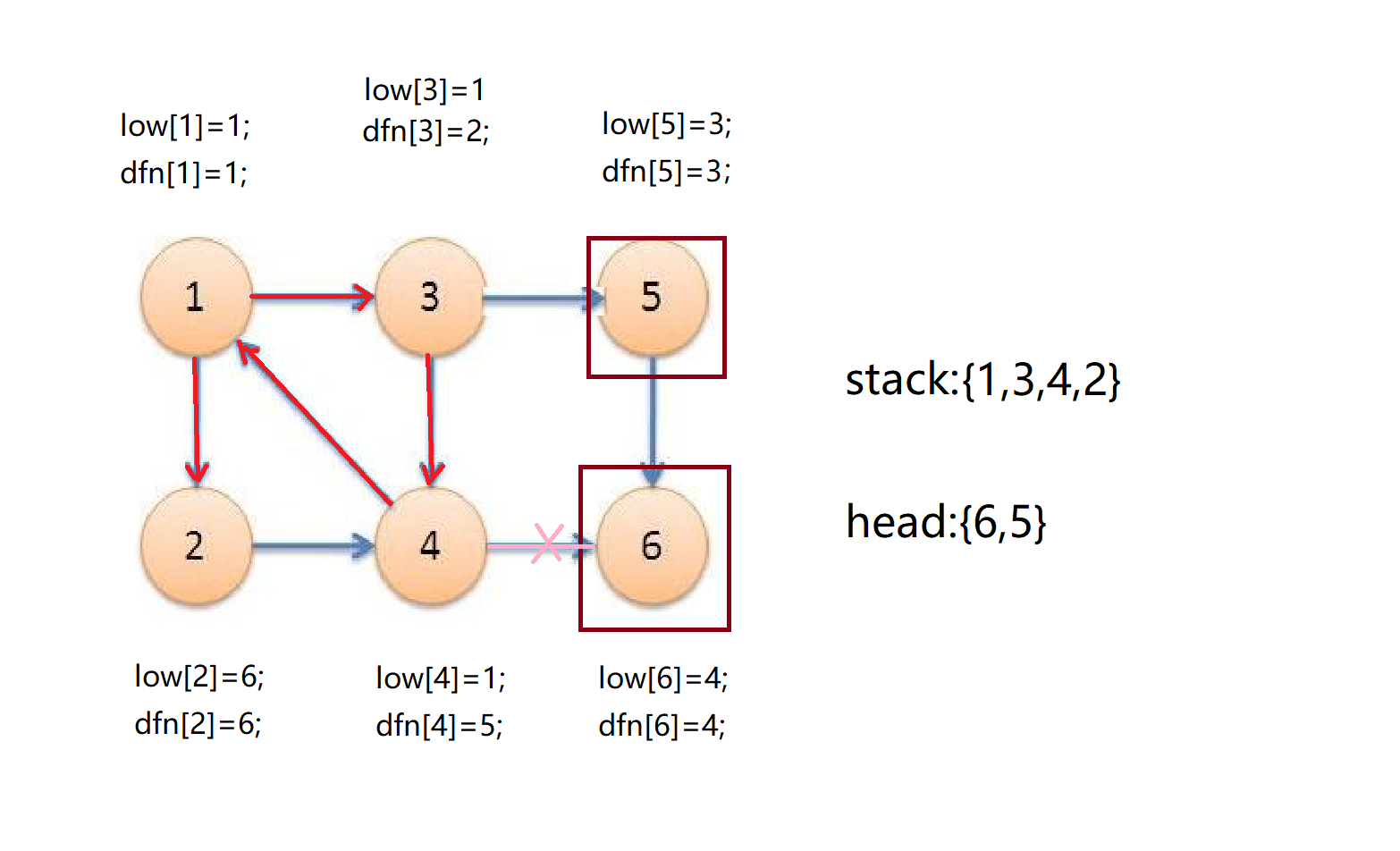
然后我们发现2只有一个儿子4，且4号点被访问过且在stack里，并且low[4]小于low[2]，所以用low[4]来替换low[2];

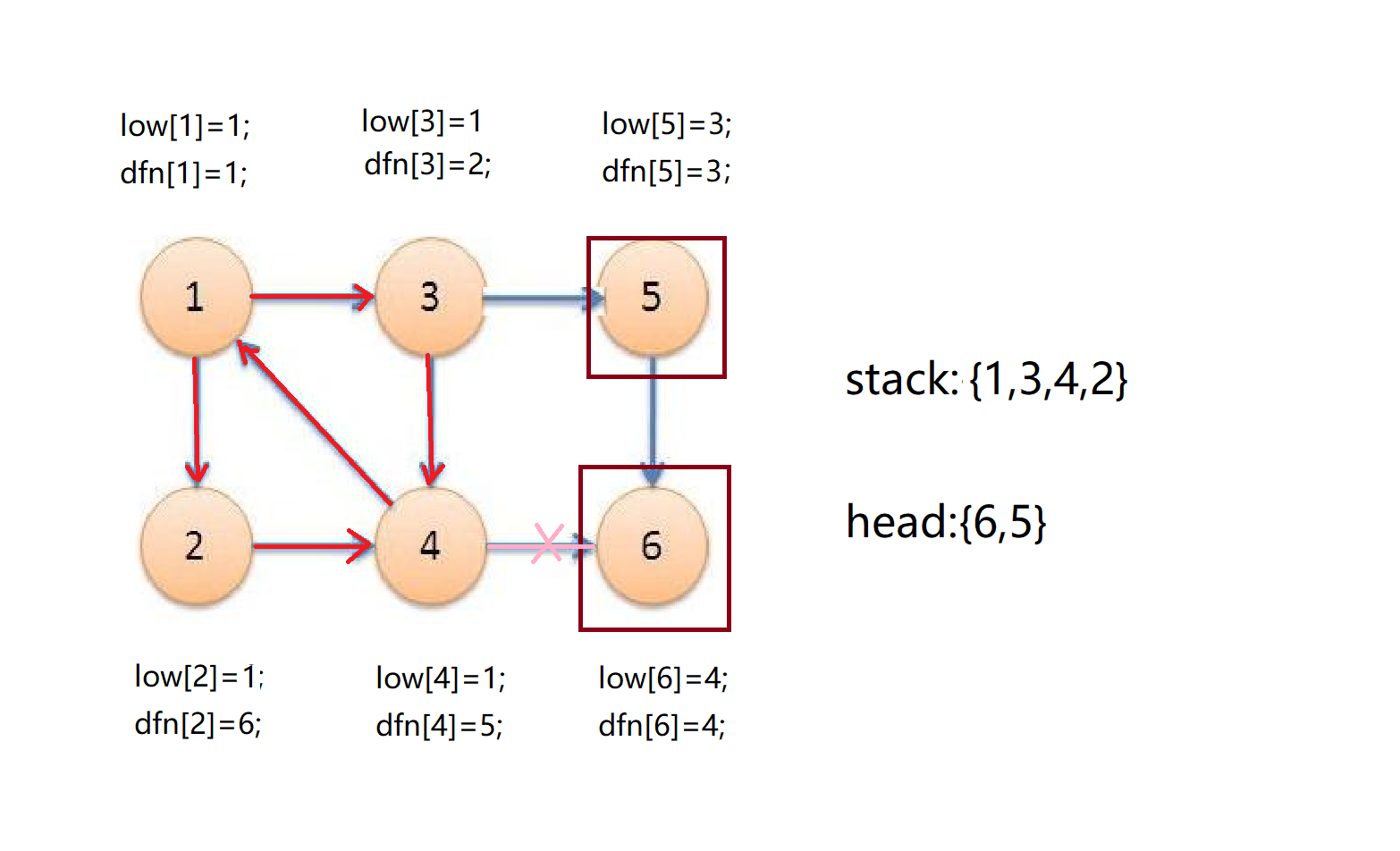
2号点没有其他儿子可以访问了，dfn[2]!=low[2],所以2号点不是某个强连通分量的头节点，我们直接退回1号点。
接着我们发现1号点也没有其他儿子可以访问了，且dfn[1]==low[1]，所以1是一个强连通分量的头元素，于是head中加一个1，把stack中1和1之后的元素退栈（有1，3，4，2），这四个点构成强连通分量。

然后我们发现全部点都被访问过了，tarjan就结束了。
【PS 若是还有点没被访问过怎么办？那就从那个点开始再跑一次tarjan，直到所以点都被遍历过】

代码实现

模板就很简单了QwQ

int tarjan(int x)
{
    tot++;dfn[x]=tot;low[x]=tot;
    stack[++indexx]=x;
    visit[x]=1;

    for(int k=last[x];k;k=a[k].next)
    {
        int y=a[k].y;
        if(dfn[y]==0)
        {
            tarjan(y);
            low[x]=my_min(low[x],low[y]);
        }
        else
if(visit[y]==1)low[x]=my_min(low[x],low[y]);

    }

    if(dfn[x]==low[x])
    {
        head[hk++]=u;
        do
        {
            fprintf(fout,"%d ",stack[indexx]);  
            visit[stack[indexx]]=0;  
            indexx--;  
        }
        while(x!=stack[indexx+1]);

        fprintf(fout,"\n"); 

    }
    return 0;

}

模板题

【caioj 1147】强连通

【题目描述】
给出一个有向图有n个点和m条有向边，输出连通分量的数量。
概念：

1. 什么是连通分量？
   答：一个有向图中，选出某些点组成一个团体，这个团体中的任意两点都可互相到达。那么：选出来的这些点+这些点之间原有的边=叫做 连通分量。
2. 只适合有向图
   答：如果是无向图，那么并查集就可以解决了（还记得“家族”吗？）
   附加1：什么是强连通图？
   答：如果有向图G的任意两个顶点都可以互相到达，称G是一个强连通图。
   附加2：什么是强连通分量？
   答：比如GG是G的最大的强连通子图，称为G的强连通分量（可能不止一个，这个不重要）
   
   比如输入样例1，有3个连通分量：（1）、（2,3,4,5,6）、（7）
   比如输入样例2，有3个连通分量：（1,2,3）、（4,6,7）、（5）
   【输入格式】
   第一行n和m（1<=n<=20000,1<=m<=20 0000），表示有向图总共n个点，点的编号由1~n。m表示m条有向边。
   下来m行，每行两个整数x和y，表示一条有向边从点x出发到点y。
   【输出格式】
   一行一个整数，表示连通分量的个数。
   【样例1输入】
   7 7
   1 2
   2 3
   3 4
   4 5
   5 6
   6 2
   5 2
   【样例1输出】
   3
   【样例2输入】
   7 11
   1 2
   1 4
   2 3
   2 5
   3 1
   3 5
   3 6
   4 6
   5 7
   6 7
   7 4
   【样例2输出】
   3

很明显就是要求强连通分量的数量，直接套模板就好了。

#include<cstdio>
#include<cstring>
#include<algorithm>
struct node
{
    int x,y,next;
}a[210000];
int last[210000];

int dfn[210000],low[210000],visit[210000],stack[210000],heads[210000];
int i,j,k,m,n,o,p,js,jl,tot,indexx,len,u,v;
using namespace std;

int my_min(int x,int y)
{
    if(x<y)return(x);
    else return(y);
}
int ins(int x,int y)
{
    len++;
    a[len].x=x;a[len].y=y;
    a[len].next=last[x];
    last[x]=len;
}

int tarjan(int x)
{
    tot++;dfn[x]=tot;low[x]=tot;
    stack[++indexx]=x;
    visit[x]=1;

    for(int k=last[x];k;k=a[k].next)
    {
        int y=a[k].y;
        if(dfn[y]==0)
        {
            tarjan(y);
            low[x]=my_min(low[x],low[y]);
        }
        else if(visit[y]==1)low[x]=my_min(low[x],low[y]);

    }

    if(dfn[x]==low[x])
    {
        js++;
        do
        {  
            visit[stack[indexx]]=0;  
            indexx--;  
        }
        while(x!=stack[indexx+1]);

    }
    return 0;

}

int main()
{
    scanf("%d%d",&n,&m);
    memset(dfn,0,sizeof(dfn));
    len=0;tot=0;indexx=0;js=0;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&u,&v);
        ins(u,v);
    }
    for(int i=1;i<=n;i++)
    {
        if(dfn[i]==0)
        tarjan(i);
    }
    printf("%d\n",js);
    return 0;
}

结语

是不是很浅显易懂呢？下篇博客我们将从tarjan其他的应用入手，带你走进你也许早已学会的tarjan算法。