在前面的很长一段时间里，我都一直在更新机器学习的内容。现在机器学习的大致内容也已过半，所以我计划利用这段时间，学习复习一些经典算法。这篇BLOG，就让我们一同来看看三种并查集算法吧！

普通并查集

并查集的概念

什么是并查集呢？并查集，是在一些有 N 个元素的集合应用问题中，体现点归属类别的树状集合。我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。

并查集是一种树型的数据结构，用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常在使用中以森林来表示。

光看概念还是下面我们来举个过年走亲戚的例子来说明一下说明是并查集。

过年了，你从大学回到家，客厅里早已坐满了人。由于你的家族人员过于庞大，要判断你和一个坐在客厅里的人是否是亲戚，确实还很不容易，所以为了拿到红包你要做足功课。通过调查，你知道了一系列的亲戚关系，比如 A 和 B 是亲戚， C 和 D 是亲戚等等…………我们约定如果 A 和 B 是亲戚， B 和 C 是亲戚， 那么 C 和 D 是亲戚。现在你想知道客厅里的有谁与你有亲戚关系？

那么我们为了简化例子，假设客厅包括你一共十个人吧，开始时你什么情报也没有掌握，所以每个人的亲戚只有他自己，我们定义同属于一棵树的就是一族亲戚：

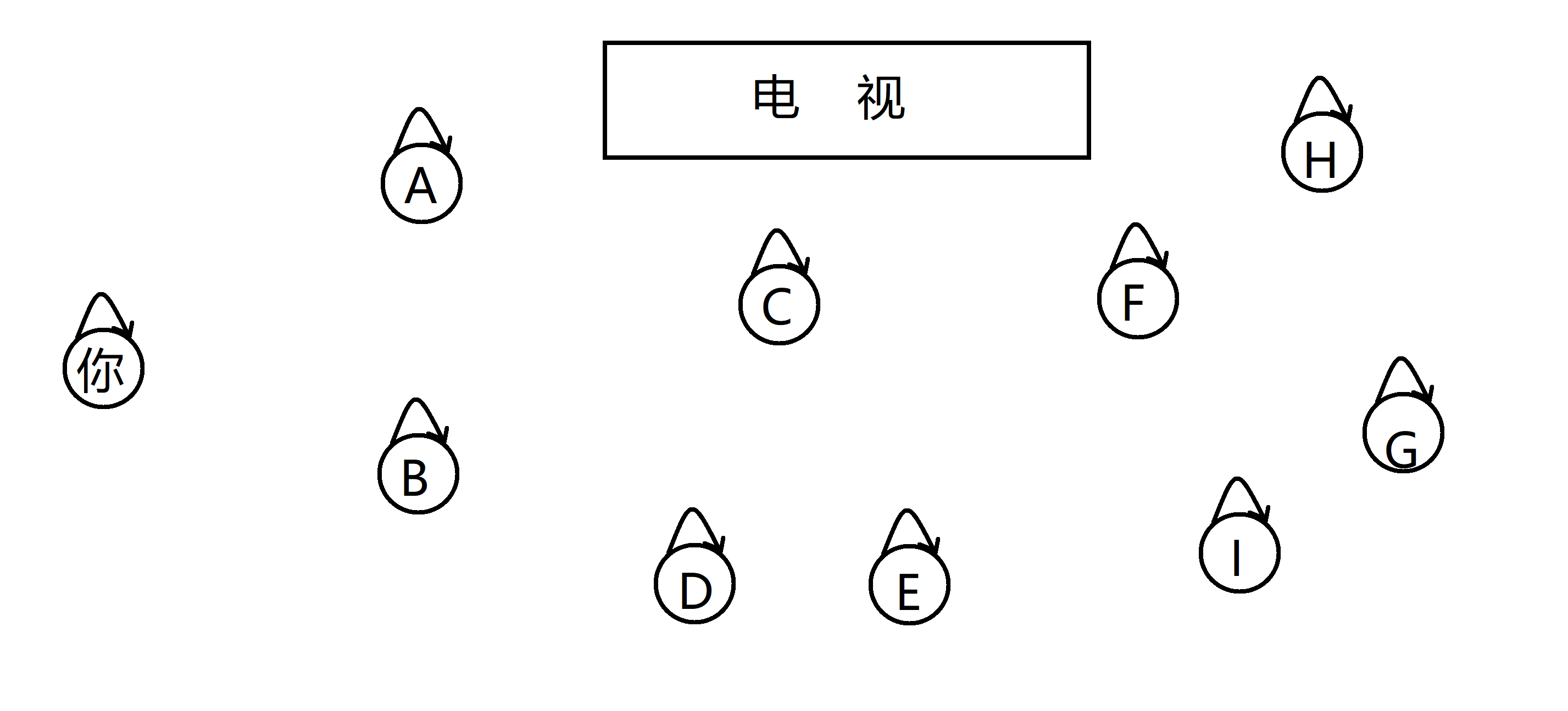
所以我们的图看起来就是一共有十棵树，每棵树只有一个点，就是他本身。接下来我们掌握到了第一条情报：C 和 E是亲戚关系，由于 C 和 E 都只是单个节点，所以我们将 C 指向 E，这样 C 和 E 就同属于一棵树，即代表他们是一族亲戚了：

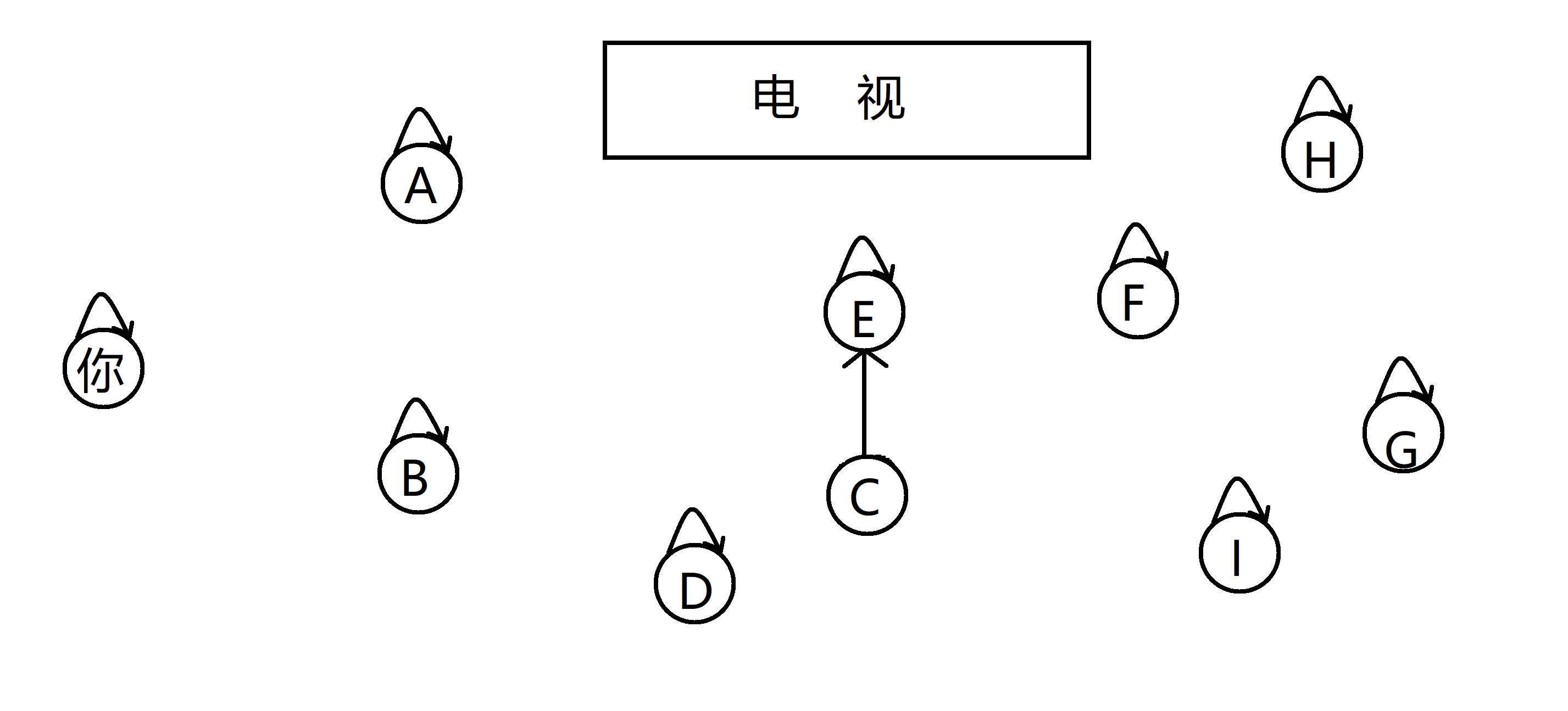
接下来你又获得了新的情报： G 和 F 是亲戚，由于 F 和 G 都只是单个节点，所以我们就直接让 G 指向 F ，让他们在同一棵树中，成为同族亲戚：

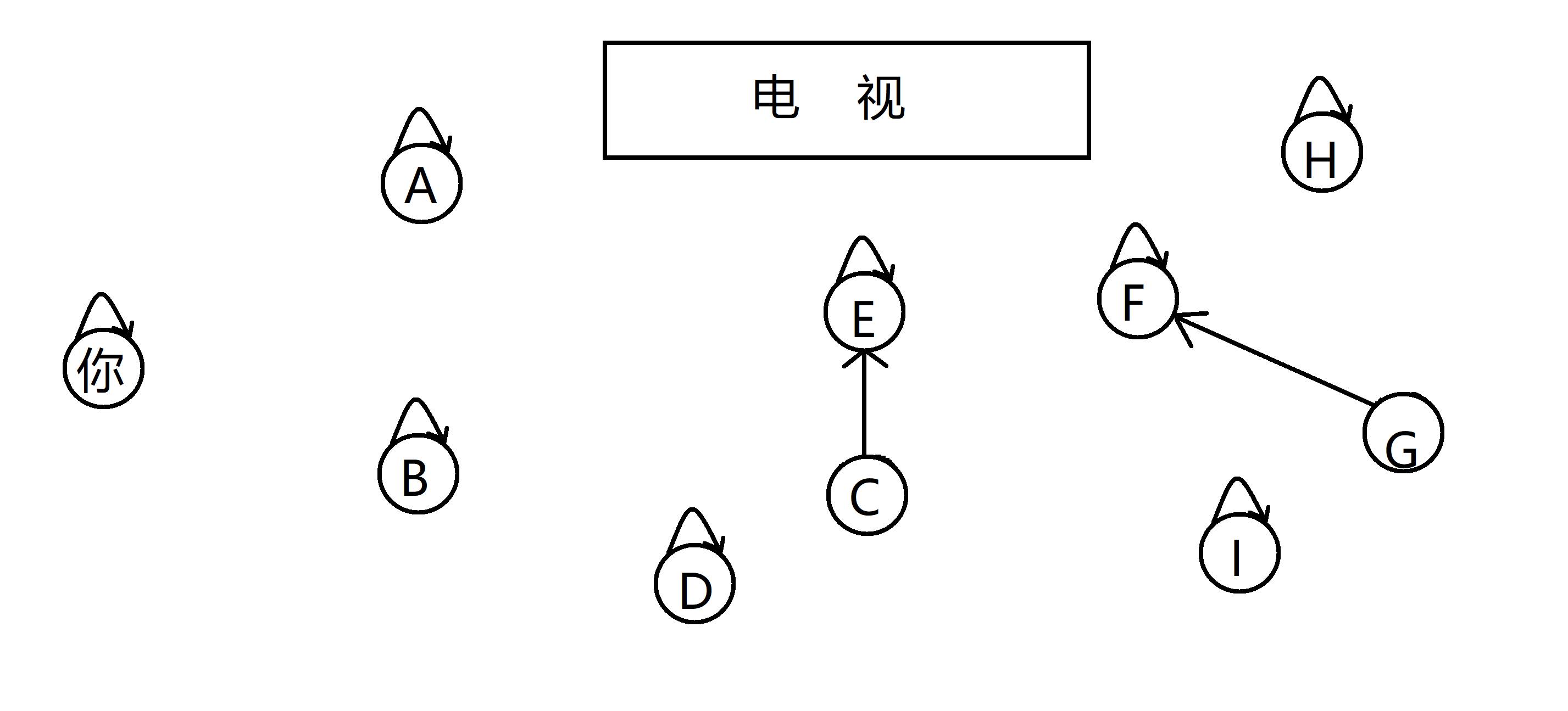
然后你发现 E 就是那个资助你上大学的舅舅，那毫无疑问他肯定是你的亲戚了，所以你指向他，加入了他的亲戚树：

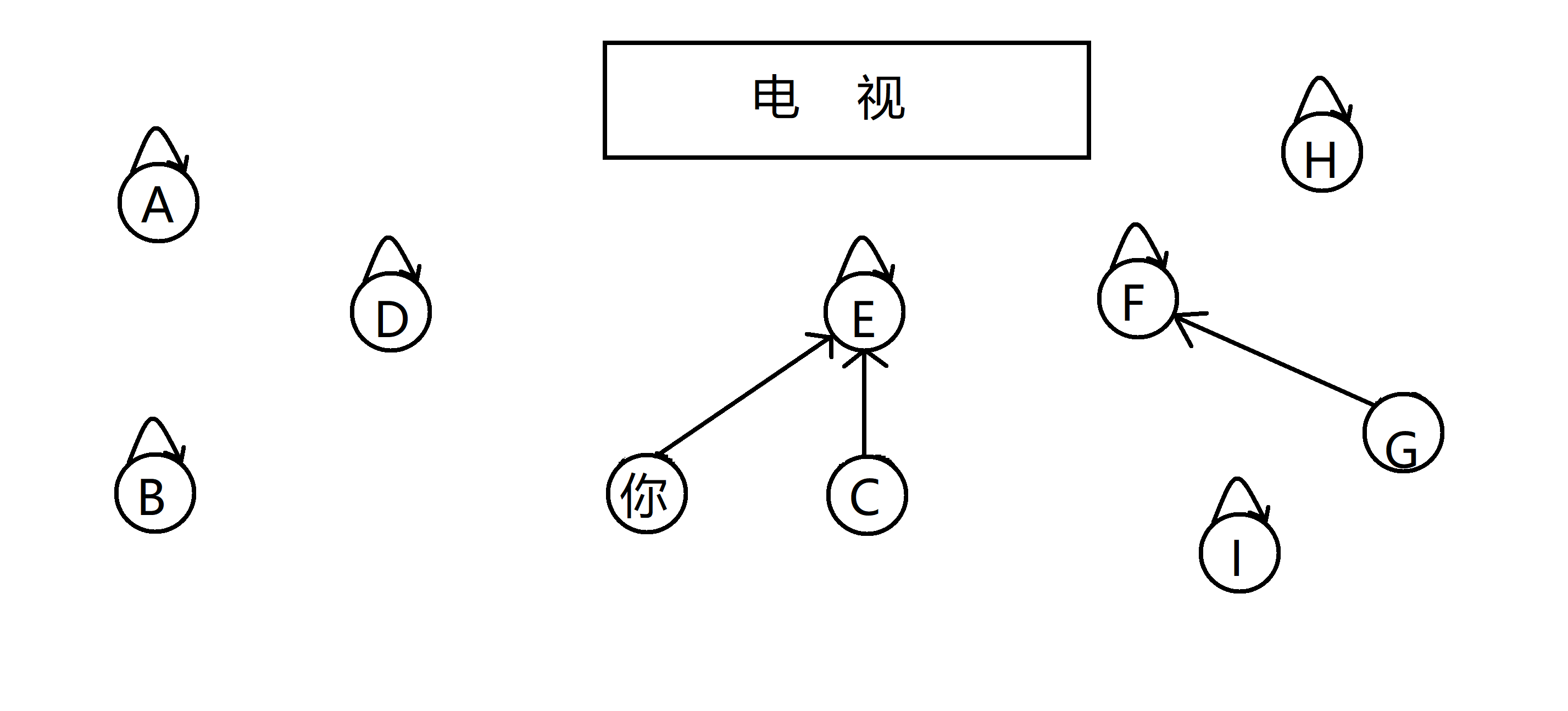
随着亲戚们聊天的深入，你发现 C 和 G 也是亲戚！但是 C 和 G都已经指向了其他节点，如果直接 C 指向 G， 那 C 和 E 的亲戚关系就无法保存了，那怎么办呢？很简单我们顺着 C 和 G 的指向，一路找到这颗亲戚树的根，也就是这个亲戚族最强大的人。比如C， 他指向 E ，我们跳到 E
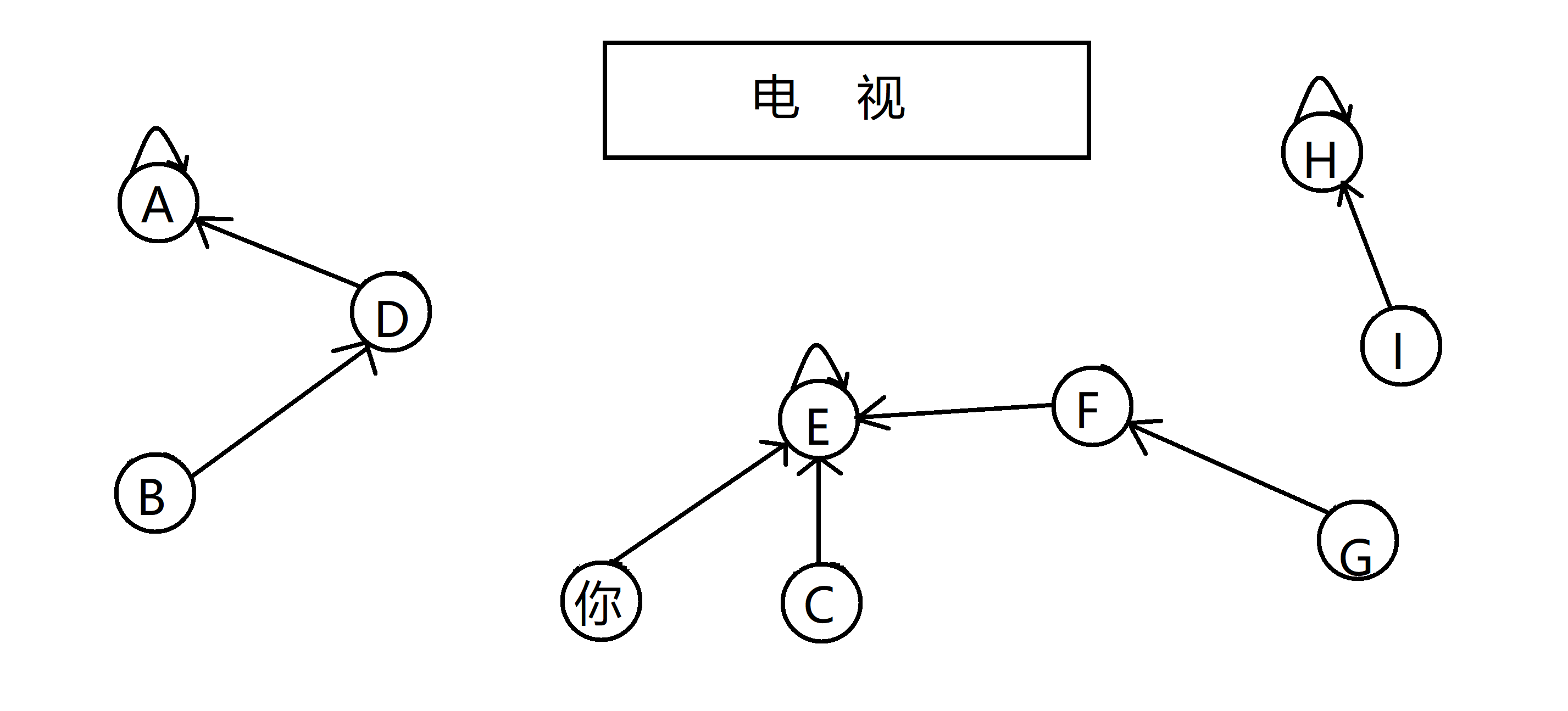
,然后发现 E 指向自己，那代表比他辈分高的人只有他自己了，换句话说 E 就是这个亲戚族群最强大的人，所以选他作为代表；同理 G 那边也选 F 作为代表，因为家族的代表开始时肯定是指向自己的，所以接着直接让 F 指向 E ，将G 所在的亲戚树合并到 C 所在的亲戚树就好了，这样他们就同处在同一棵亲戚树下了：

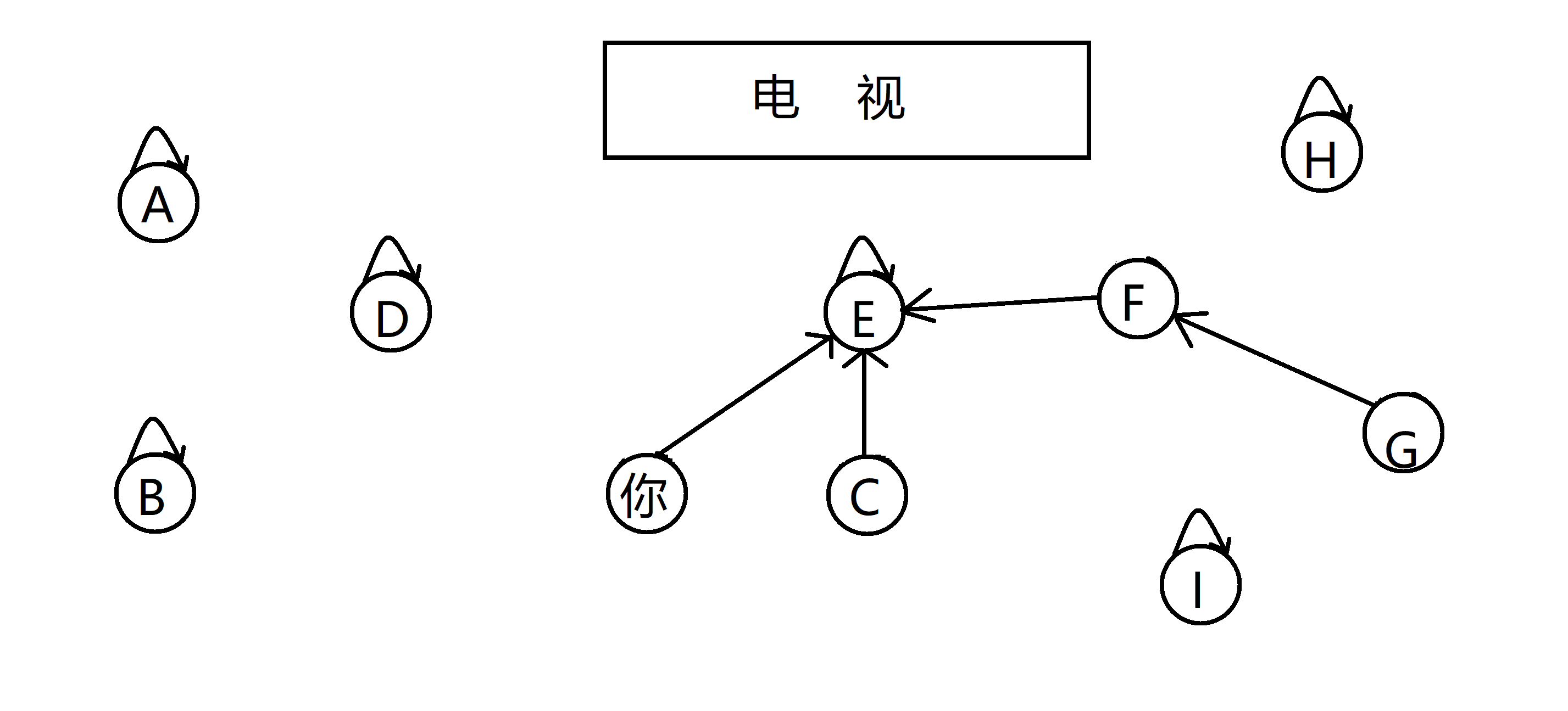
通过多次合并，你发现，客厅里其实就是由这三个族群组成的，而与你有亲戚关系的人就是和你在同一棵树的 C E F G：

这样我们就完成了并查集这个算法，是不是很简单呢。

代码实现

下面我们来看看并查集的具体实现，其实主要就分为三个部分：初始化，寻找根节点和合并操作，下面我们一个一个来看看吧。

初始化

在上面那个例子中，我们看到，在最开始的时候，每个集合都只有他自己一个人，每个家族也只有一个人。换句话说，自己就是自己这个家族的代表，所以初始化所有人都指向他自己，也可以看成所有人的父亲节点都是他自己：

for(int i = 1; i <= n; i++) {
    fa[i] = i;
}

寻找根节点

普通的实现方法

按照我们刚刚的思路，要找到点 u 所属的那棵亲戚树的代表人，也就是要找到这棵树的根节点，我们只需要从 u 开始一直想父亲节点迈进，直到找到一个点的父亲节点是他本身就可以了，所以我们可以通过递归实现：

int find(int u) {
    if(fa[u] == u) return(u);
    else return(find(fa[u]));
}

路径压缩的实现

但是刚刚这个算法有个致命的弱点，虽然是树状结构，但可能由于多次合并退化成链，所以导致每次查询都非常慢：

所以为了解决这个问题，我们有一种叫做路径压缩的方法。其思想就是将我们链状的路径压缩成扫把装。其实现方法就是每次查询点 u 所在树的根节点的时候，在递归返回的时候，把 u 到根节点链上的说有点的父亲节点都设置成这个根节点，这样我们最后就会得到一个扫把状的树，在上个例子中压缩后这条链的深度从 5 变成了 2 ，查询效率大大增加：

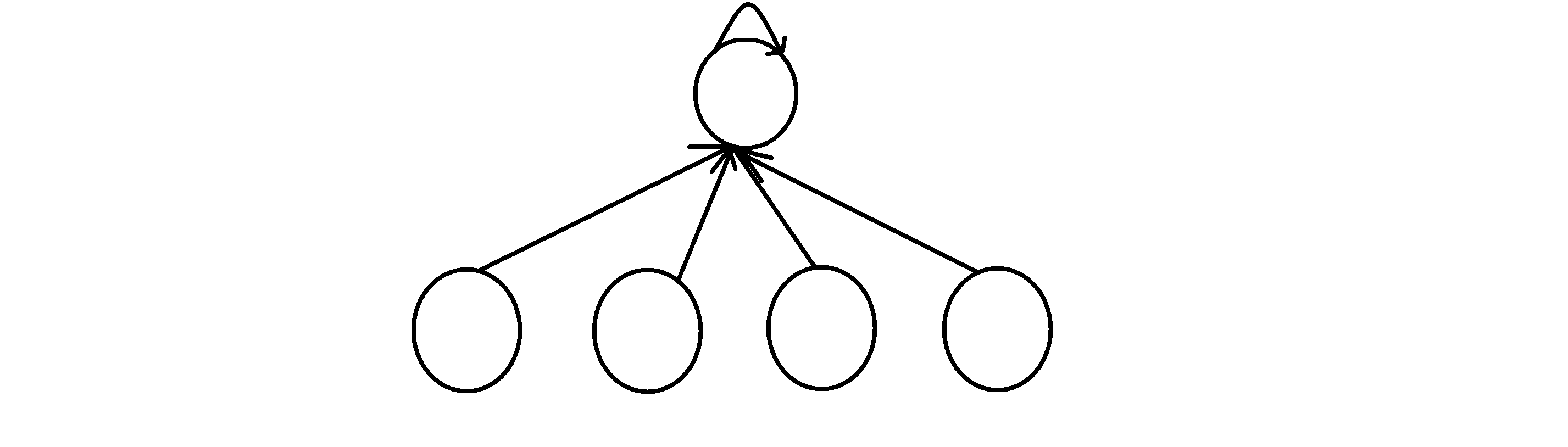
具体的代码实现也很简单，就如下：

int find(int u) {
    if(fa[u] == u)return(u);
    else {
        fa[u] = find(fa[u]);
        return(fa[u]);
    }
}

合并两个集合树

合并的思想也很简单，对于两个点 u 和 v ，先找到 u 和 v 所在并查集的根节点 fau 和 fav，然后进行如下判断。如果 fau == fav，就说明他们本身就在一个并查集，也就是同一棵树下，所以不需要再合并了；反之则将 fau 指向 fav，即把 fau 的父亲设置为 fav。代码实现也很简单：

void merge(int u, int v) {
    int fau = find(u);
    int fav = find(v);
    if(fau != fav) fa[fau] = fav;
    return ;
}

经典例题

Luogu[p3367 并查集]

题目描述
如题，现在有一个并查集，你需要完成合并和查询操作。

输入格式
第一行包含两个整数 N,M ,表示共有 N 个元素和 M 个操作。

接下来 M 行，每行包含三个整数 Xi,Yi,Zi.当 Zi = 1时，将 Xi 与 Yi 所在的集合合并。

当 Zi = 2 时，输出 Xi 与 Yi 是否在同一集合内，是的输出 Y ；否则输出 N 。

输出格式
对于每一个 Zi = 2 的操作，都有一行输出，每行包含一个大写字母，为 Y 或者 N 。

输入输出样例
输入 #1
4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4
输出 #1
N
Y
N
Y

其实这道题就是并查集的模板题了，和我们之前亲戚的例子有异曲同工之妙，下面直接贴出模板：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
int fa[11000];
int n, m ,k, u, v, fau, fav;
int find(int u) {
    if(fa[u] == u)return(u);
    else {
        fa[u] = find(fa[u]);
        return(fa[u]);
    }
}//寻找并查集根节点
int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++)fa[i] = i;
    for(int i = 1; i <= m; i++) {
        scanf("%d%d%d", &k, &u, &v);
        if(k == 1) {
            fau = find(u);
            fav = find(v);
            if(fau != fav) fa[fau] = fav;
            //相当于merge函数
        }
        else {
            fau = find(u);
            fav = find(v);
            if(fau != fav)printf("N\n");
            else printf("Y\n");
        }
    }
    return 0;
}

带权并查集

算法原理

带权并查集顾名思义就是带有权值的并查集，一般我们见到的都是带有边权的带权并查集，那带权并查集有什么用呢？下面我们就来通过一个例子看看吧！

有一个一个长为N（N ≤ 1e9）的 01 串，给你 M（M ≤ 1e4）条区间信息，每条信息给定一个区间[l, r]，告诉你[l, r]中 1 的个数的奇偶性，问那句话最先和前面的话起冲突？

这道题既然归纳在带权并查集这个框体，那就一定可以用带权并查集解决。先不管带权并查集到底是个啥，我们的主要思想就是，假如第 k 句话是和之前有冲突的的，那我们就要通过前 k - 1 句话去建立一个并查集一样的图，去推翻我们的第 k 句话。

接下来我们来分析一下题目。首先我们看到 N 很大， M 挺小，并查集又离不开 fa[] 数组，如果直接存 N 范围内所有点的 fa[] 数组肯定要爆内存，所以我们想到的第一件事就是离散化，每条信息给我们左右两个端点，离散化下来最多就剩下 2e4 个点，这是可以接受的。

那离散化后我们怎么处理呢？我们继续分析题目，每条信息都会告诉我们一个区间的 1 的数量的奇偶性。那看到奇偶性，我们就很自然的想到奇偶性的一些性质：偶数 + 偶数 = 偶数，奇数 + 奇数 = 偶数，奇数 + 偶数 = 奇数。所以看到这样的奇偶性，我们就可以考虑前缀和，用 sum[i] 来表示前 i 个数中 1 的个数。

为什么是前缀和呢？我们看下图，我们假设一个线段表示一个数，假如我们得到情报说这段蓝色区间[l, r]中 1 的个数是偶数，那就代表紫色区间减去绿色区间这两个前缀和相减得到的是偶数，即sum[r] - sum[l - 1] = 偶数，换句话说这两个前缀和奇偶性相同：

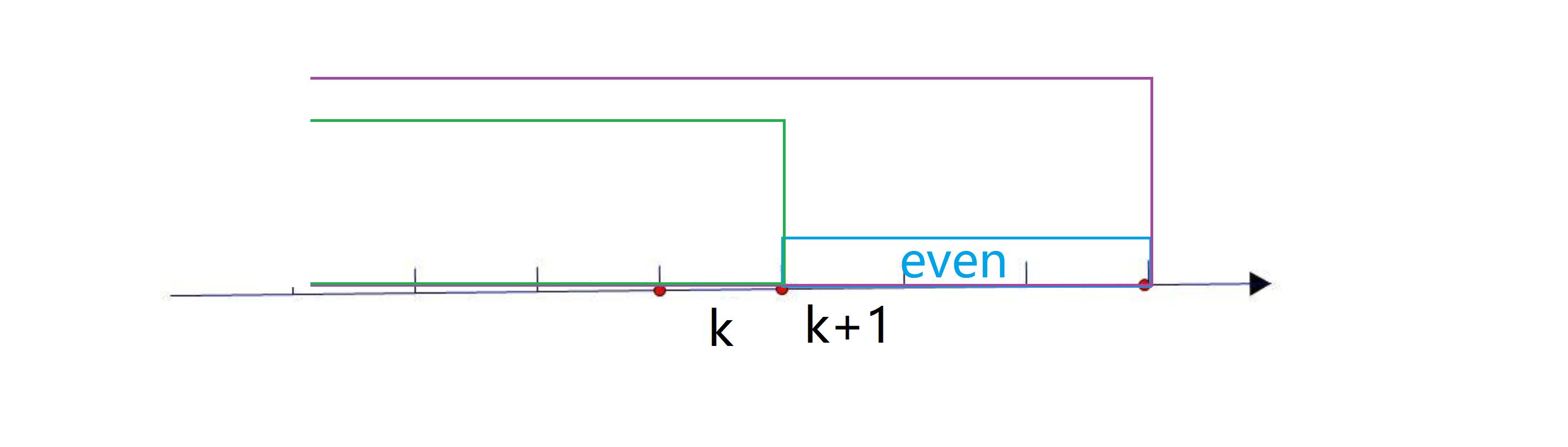
同理如果我们得到情报说这段蓝色区间[l, r]中 1 的个数是奇数，那就代表紫色区间减去绿色区间这两个前缀和相减得到的是奇数，，即sum[r] - sum[l - 1] = 奇数，换句话说这两个前缀和奇偶性相反：

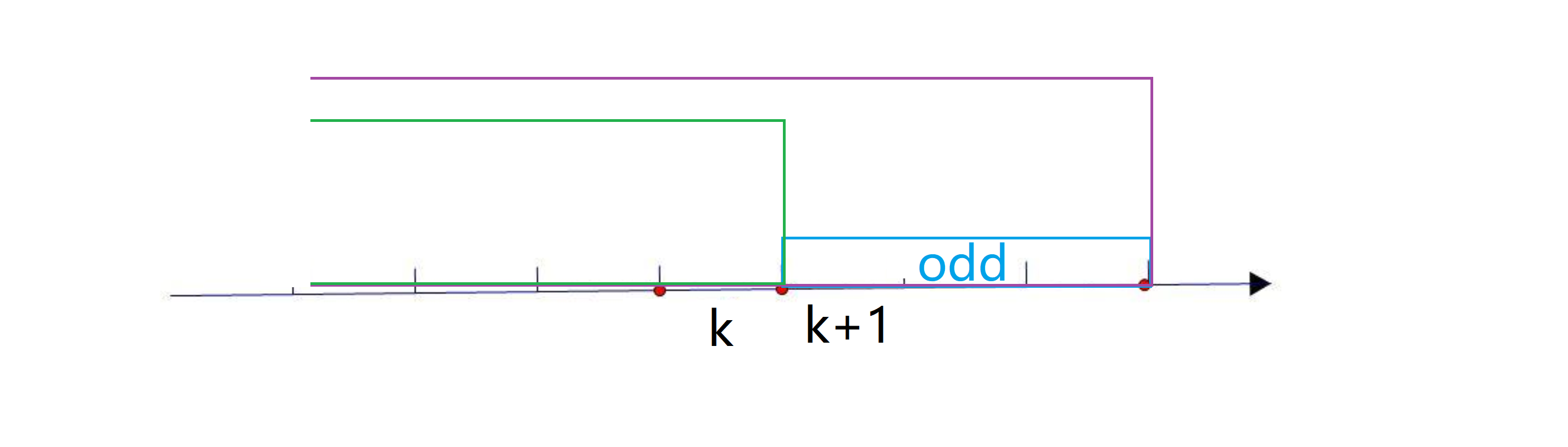
所以我们就可以利用 sum[r] 和 sum[l - 1] 的奇偶的相同或相反性建立并查集。我们通过设计并查集边权的形式来表示几个前缀和的相对奇偶性，我们设 dis[i] 为点 i 到其父亲节点 fa[i] 边上的边权。我们约定，如果一个点 i 所代表的前缀和 sum[i] 和其父亲点 fa[i] 所代表的前缀和 sum[fa[i]] 的奇偶性相同，那边权就为 0；若奇偶性相反，边权就为 1：

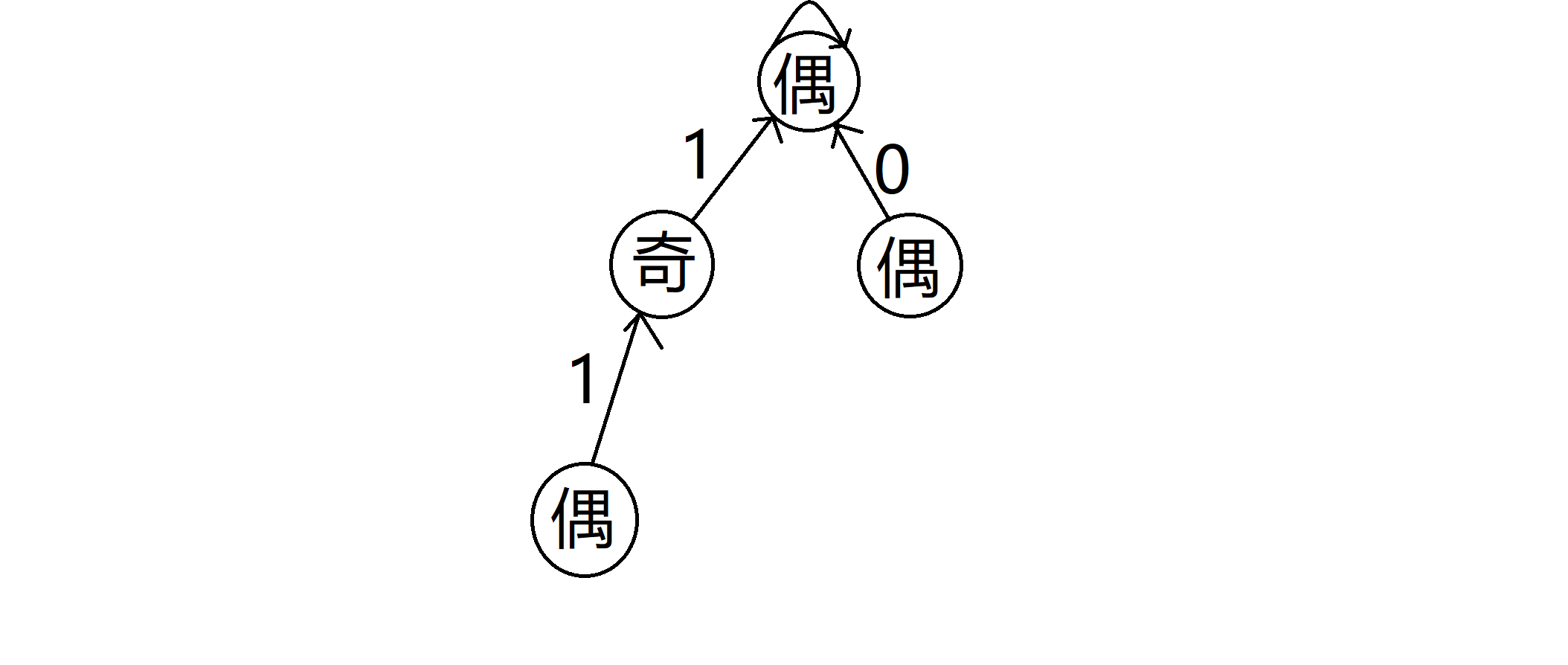
而这样做有什么好处呢？这样做我们可以利用异或的性质去判断一个并查集上的任意两两点的奇偶性是否相等。我们找到一个点 X，一个点 Y，我们把并查集上 X 到 Y 上的所有边权异或起来。若为 0，则两点奇偶性相同；若为 1 ，则奇偶性不同：

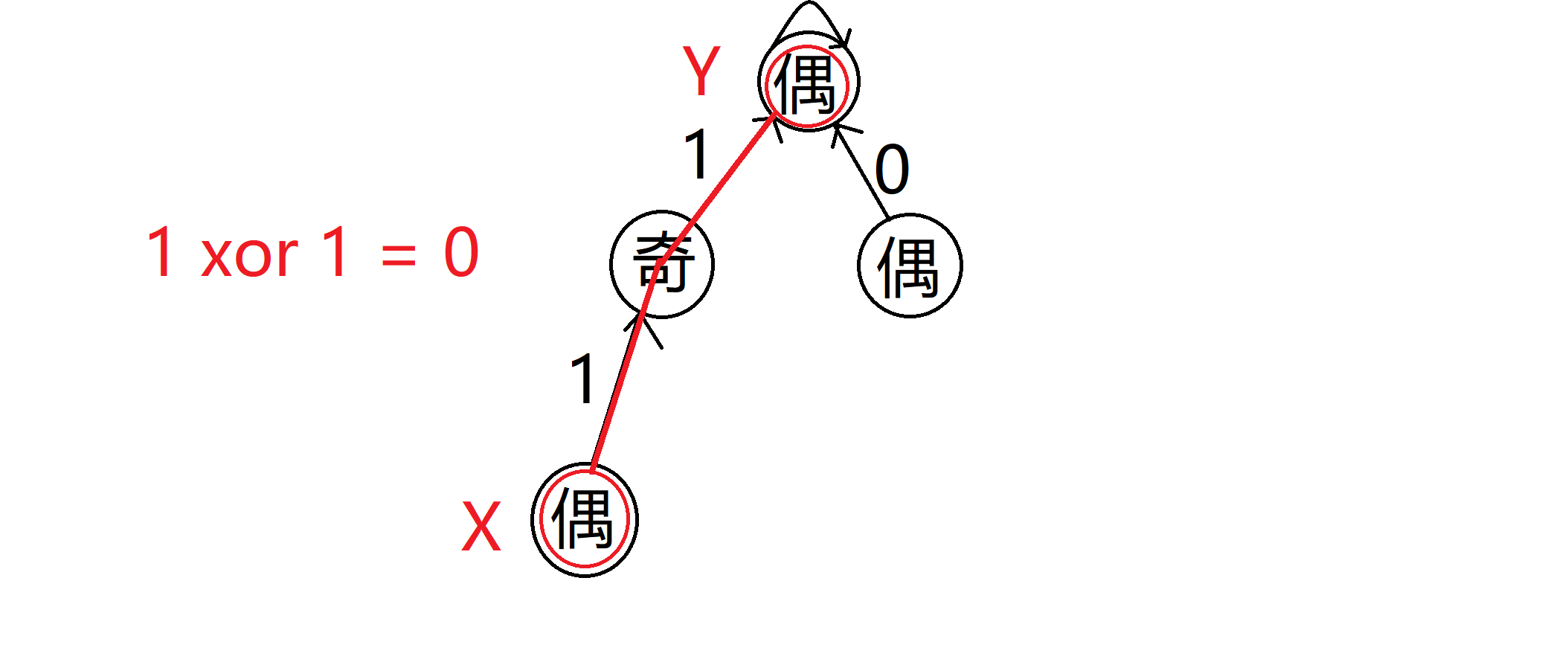
所以我们的维护方法就很明朗了。每次读入一个区间信息，我们首先先判断一下两个区间端点是否在同一个并查集上。换句话说我们要先 find(l - 1) 和 find(r)，顺便进行路径压缩，看看祖先是不是同一个节点。但是由于我们此时的并查集是带边权的，所以这个路径压缩就是有讲究的了。在路径压缩 x 点的时候，它会直接指向祖先节点，那边权怎么确定呢？其实很简单，因为在路径压缩 x 之前，他的父亲节点一定压缩好了，所以他的深度就是 3 ，就是我们上面这个例子的 X 点，Y 就是祖先节点结合上面那个例子，你就知道他指向根节点时，dis[i] = dis[fa[i]] xor dis[i];就可以了。

那如果此时我们发现 l - 1 和 r 这两个点是位于同一棵并查集上，那我们接着就要判断这条信息给出的奇偶性的真假。通过之前的 find 操作，我们的 l - 1 和 r 都时祖先的直接孩子了，设边权分别为 dis[l - 1] 和 dis[r]:

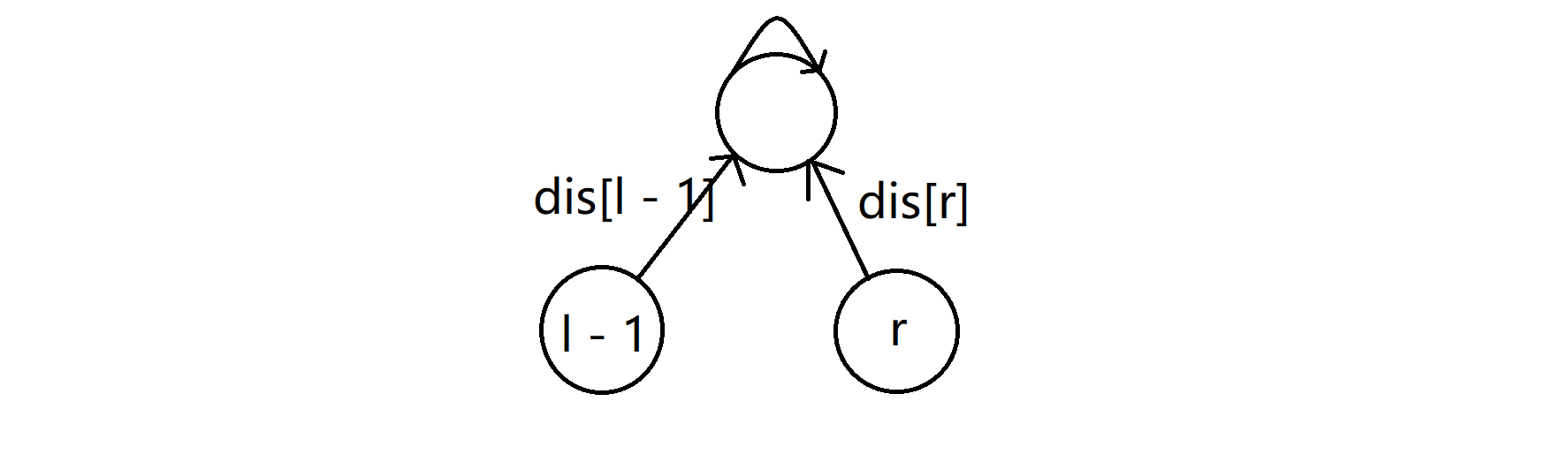
那我们就可以很显然地运用dis[l - 1] xor dis[r]来判断 l - 1 和 r 的奇偶性，若结果是 0 ，则两者奇偶性相同，若结果是 1，则两者奇偶性相反。

那如果 l - 1 和 r 不在同一个并查集上，那我们就要合并两棵并查集。接下来我们来考虑如何合并两棵并查集。由于经过了路径压缩，我们的 l - 1 号点和 r 号点都是他们祖先的孩子：

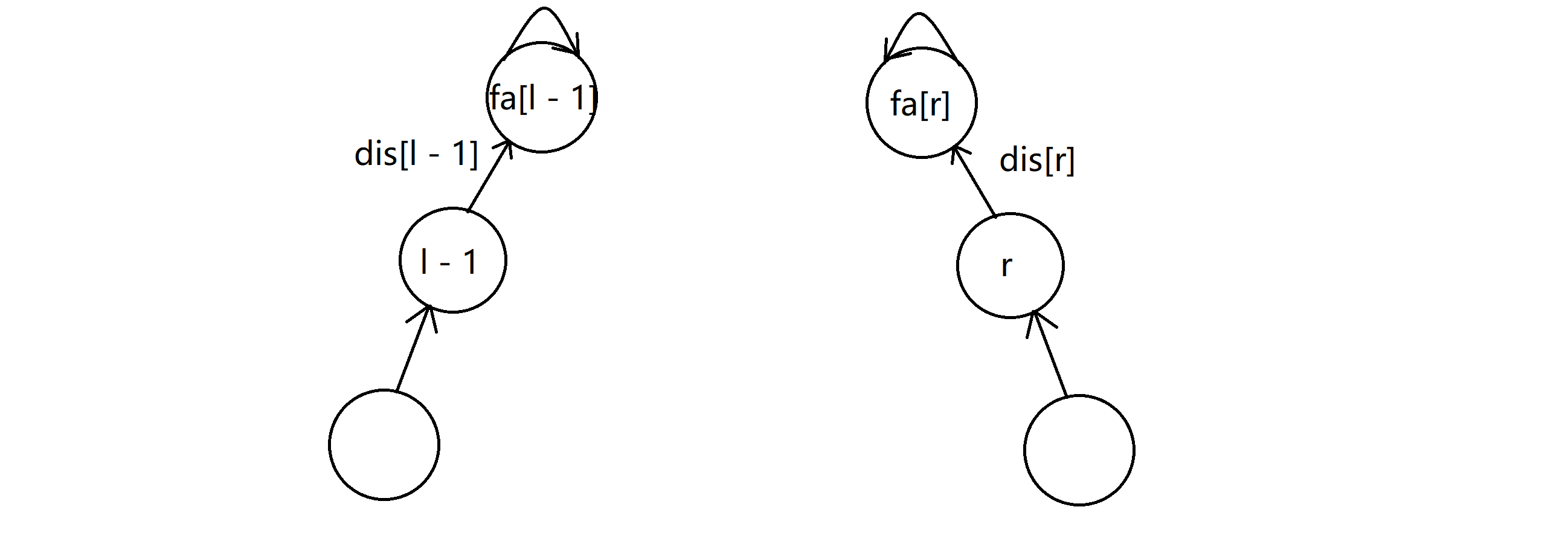
那首先根据普通并查集的合并方法，我们肯定先让 fa[l - 1] 指向 fa[r];换句话说就是设置 fa[fa[l - 1]] = fa[r]，那剩下的问题就是，新增的这条边的边权 v 怎么确定？

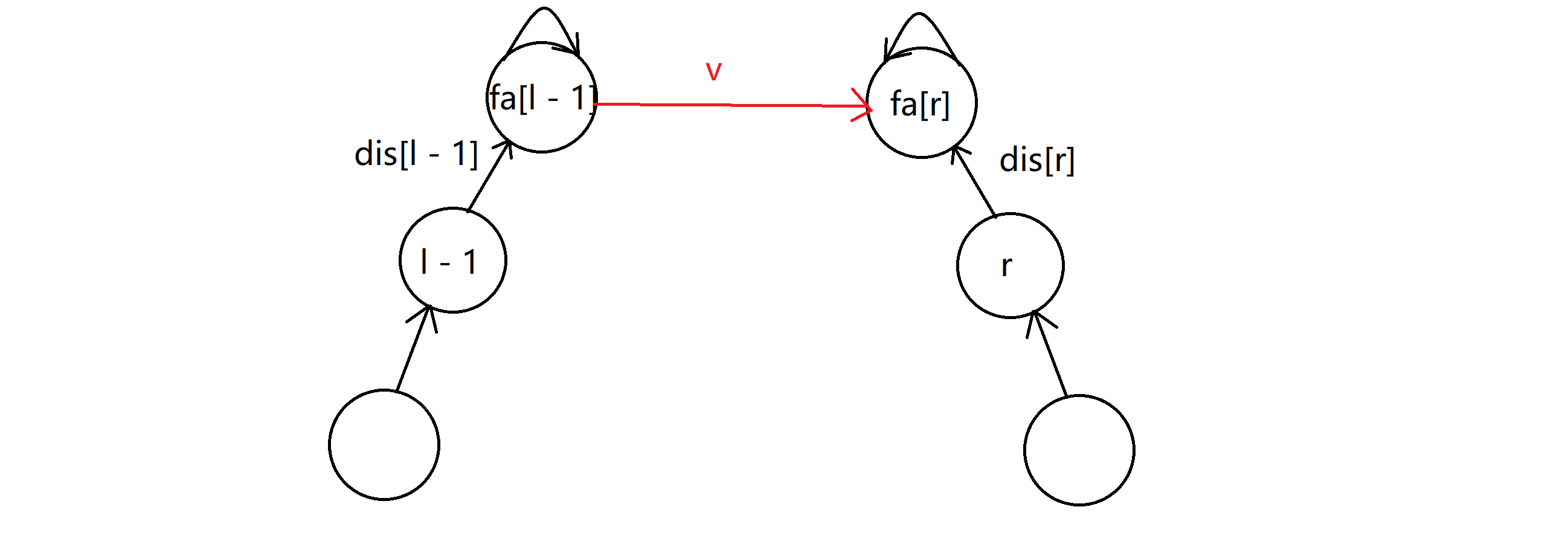
我们来分情况看看，如果我们得到情报说 l - 1 和 r 的奇偶性相同，那就是 l - 1 到 e 的路径上的边异或起来要等于 0 ，即dis[l - 1] xor v xor dis[r] = 0，根据异或的性质，我们可以把除了 v 以外的项都移动到右边，得到v = dis[l - 1] xor dis[r] xor 0;同理当 l - 1 和 r 的奇偶性相反时，我们有v = dis[l - 1] xor dis[r] xor 1。为了把上面两条式子统一起来，我们可以设 e[i] 代表第 i 条情报信息，若情报显示两者奇偶性相同，则 e[i] = 0;反之 e[i] = 1。

这样我们就完成了带权并查集对这道问题的解决。

算法实现

具体思路在上面已经基本介绍清除了，下面我们来看看这个问题的实现方法。下面是带权并查集的模板：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
struct node {
    int num, site, rank;
}a[11000];
int fa[11000], dis[11000], e[11000];
int n, m, tot = 0, rankk = 0, fax, fay, x, y;
char s[10];
bool compa(node x, node y) {
    if(x.num < y.num)return(true);
    else return(false);
}
bool compb(node x, node y) {
    if(x.site < y.site)return(true);
    else return(false);
}

int find(int x) {
    if(fa[x] == x) return(x);
    else {
        find(fa[x]);
        dis[x] = dis[x] xor dis[fa[x]];
        fa[x] = fa[fa[x]];
        return(fa[x]);
    }
}//寻找祖先 
int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= m; i++) {
        tot++; scanf("%d", &a[tot].num); a[tot].site = tot; a[tot].num--;//l - 1
        tot++; scanf("%d", &a[tot].num); a[tot].site = tot;//r
        scanf("%s", s + 1);
        if(s[1] == 'e') e[i] = 0;
        else e[i] = 1;
    }
    sort(a + 1, a + tot + 1, compa);
    a[0].num = a[1].num - 1;
    for(int i = 1; i <= tot; i++) {
        if(a[i].num > a[i - 1].num) rankk++;
        a[i].rank = rankk;
    }//离散化 
    sort(a + 1, a + tot + 1, compb);

    for(int i = 1; i <= rankk; i++) {
        fa[i] = i;
        dis[i] = 0;
    }//初始化 

    for(int i = 1; i <= m; i++) {
        x = a[i * 2 - 1].rank; y = a[i * 2].rank;
        fax = find(x); fay = find(y);

        if(fax == fay) {
            if((dis[x] xor dis[y]) != e[i]) {
                printf("%d\n", i - 1);
                exit (0);
            }//如果这句话和之前矛盾 
        }
        else {
            fa[fax] = fay;
            dis[fax] = dis[x] xor dis[y] xor e[i];
            //合并两棵并查集 
        }
    }
    printf("%d\n", m);
    return 0;
} 

扩展域并查集

算法原理

接下来我们来看并查集中的一种奇淫异巧，叫做扩展域并查集。那什么是扩展域并查集呢？我们还要用上面这个题目作为例子。

有一个一个长为N（N ≤ 1e9）的 01 串，给你 M（M ≤ 1e4）条区间信息，每条信息给定一个区间[l, r]，告诉你[l, r]中 1 的个数的奇偶性，问那句话最先和前面的话起冲突？

但这次我们的做法有些不同，我们在离散化过后，我们开两倍的节点。换句话说，我们每个位置 i 都开两个节点，一个代表 sum[i] 是奇数，一个代表 sum[i] 是偶数：

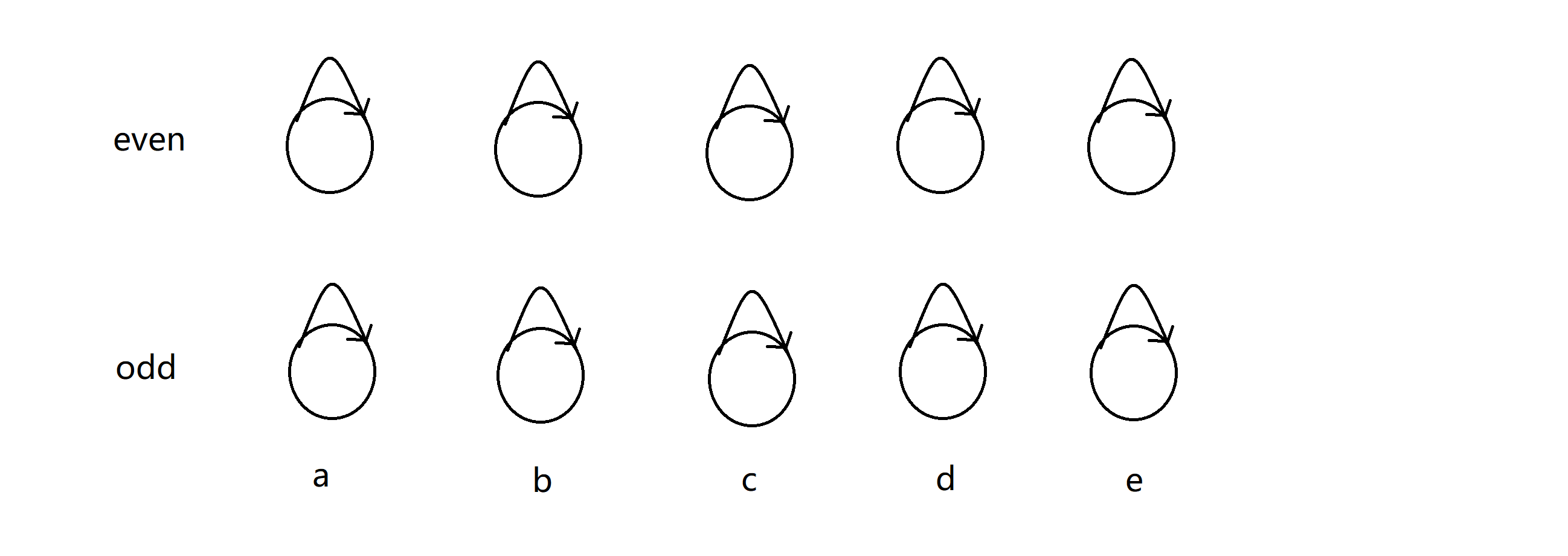
在之前的并查集中，身处同一棵并查集的元素我们把它们看成同一类。但是在扩展域并查集中，身处同一棵并查集下的 x 和 y 表示的则是 x 成立则 y 一点成立，反之亦然。比如 x 是偶数的话， y 一定是奇数之类的。

所以我们应该怎么维护呢？就对于上面这幅图吧。假如我们知道 sum[a] 和 sum[b] 奇偶性相同，首先我们先查找 a 和 b 的奇偶性相反的点是否在一个并查集，如果是那就代表之前的证据表明，如果 sum[a] 与 sum[b] 的奇偶性相反!如果没有，就看看 a 和 b 奇偶性相同的点在不在一棵并查集上，如果不在，插入以下边，合并到一棵并查集上。也就是说如果 sum[a] 是奇数， sum[b]就是奇数；sum[a] 是偶数， sum[b]就是偶数：

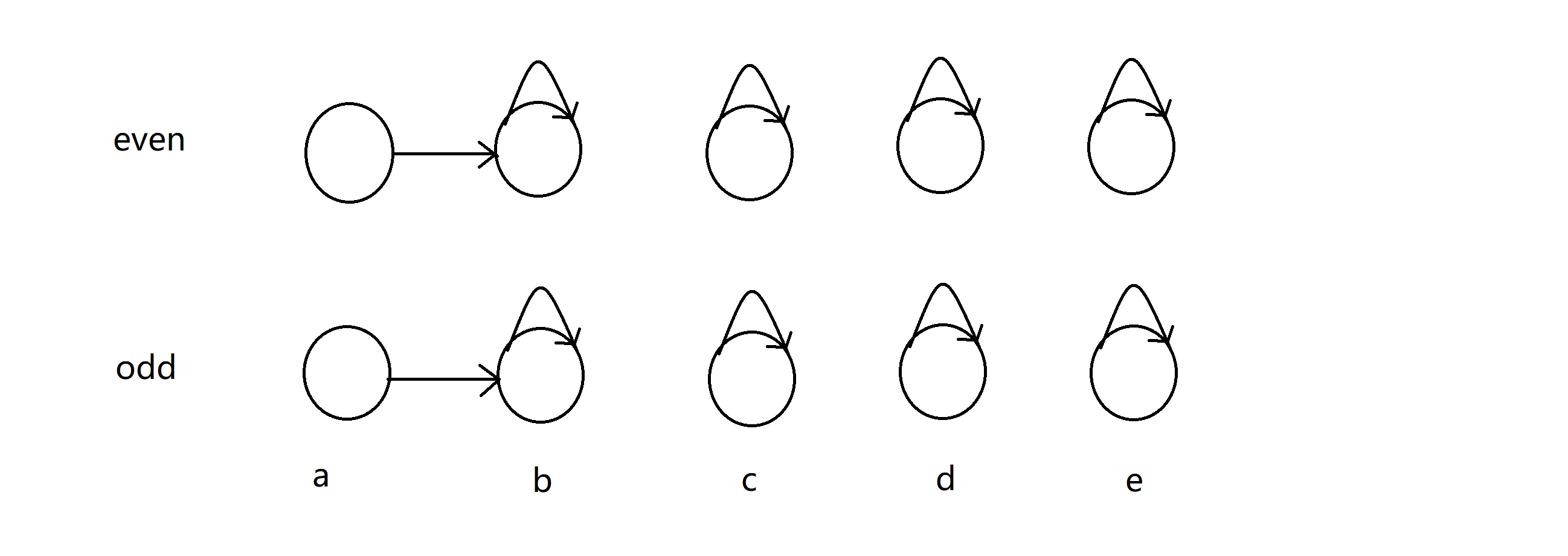
接着我们知道 sum[b] 和 sum[c] 的奇偶性相反，类似地，我们验证了他们不冲突后，就添加如下边，代表如果 sum[a] 是奇数， sum[c]就是偶数；sum[a] 是偶数， sum[c]就是奇数：

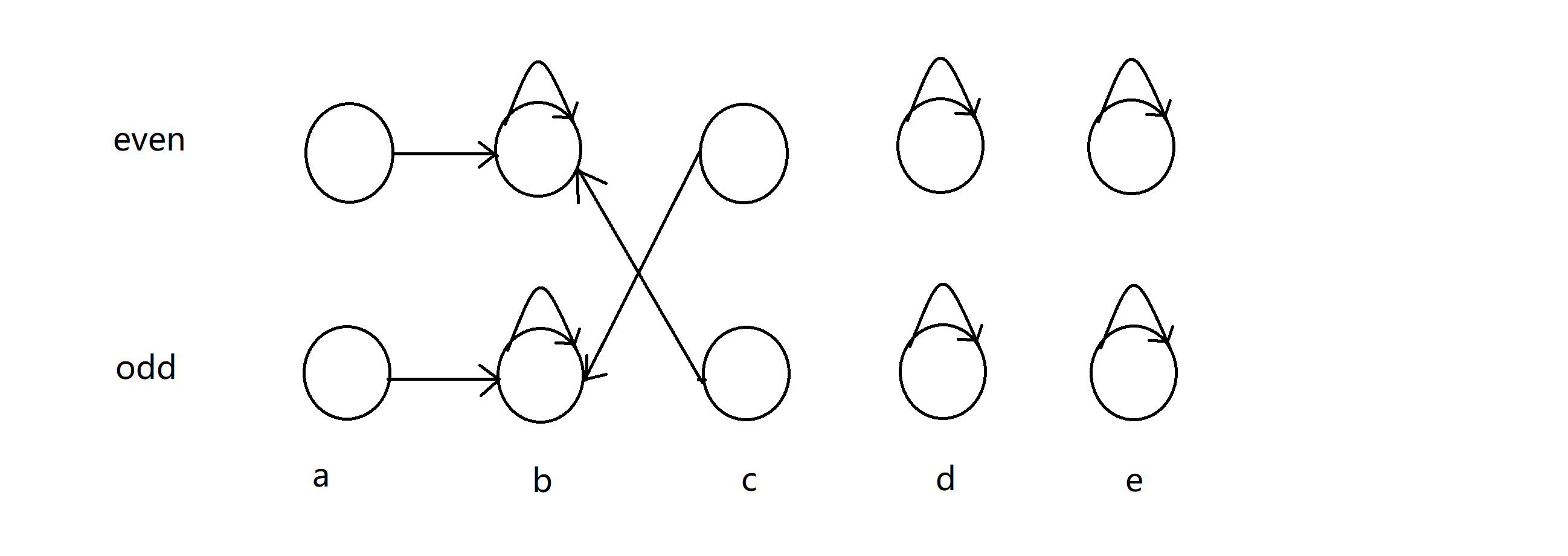
好这时，如果我们知道 sum[a] 和 sum[c] 奇偶性相同，那我们首先验证，a 和 c 奇偶性相反的点是否在一个并查集上，我们一看，完了出事了！在一个并查集上（下图中蓝色点和绿色点），那这就证明这句话是假话，输出即可。

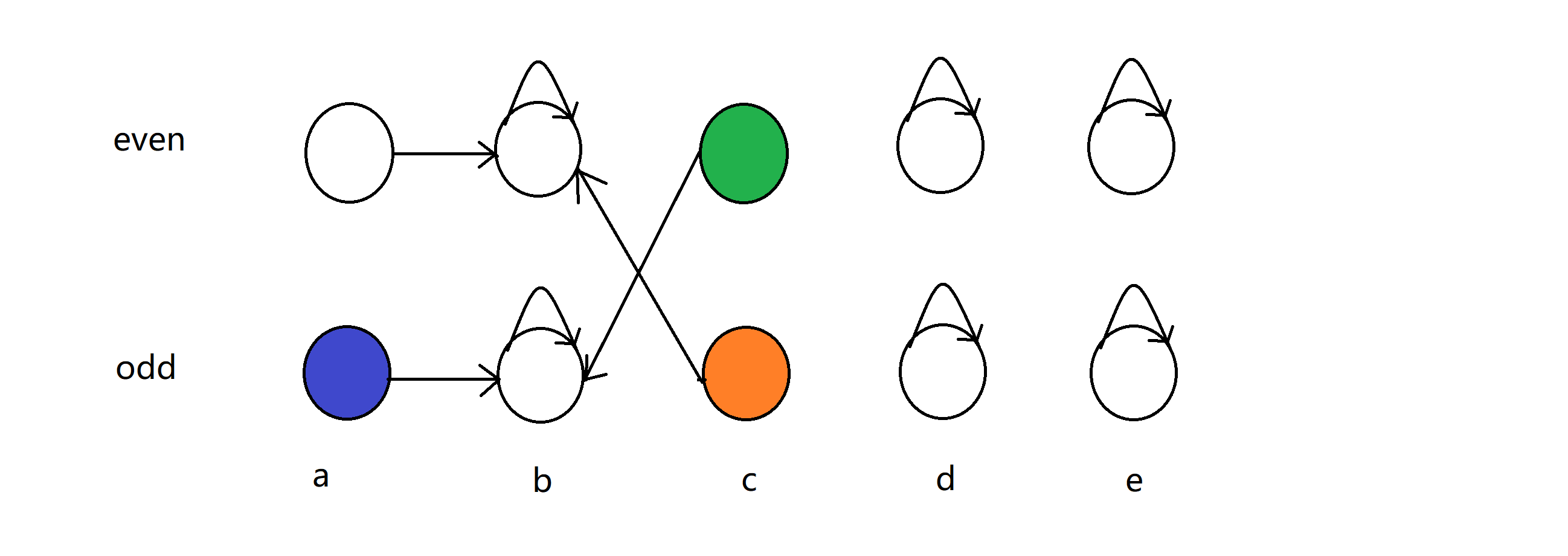
以上就是我们扩展域并查集的维护方法，是不是更加简单呢？

算法实现

思路如此简洁，算法的实现也很简单。上面那题的模板见下：

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
struct node {
    int num, site, rank;
}a[11000];
int fa[22000],  e[11000];

int n, m, tot = 0, rankk = 0, fax, fay, x, y;
char s[10];
bool compa(node x, node y) {
    if(x.num < y.num)return(true);
    else return(false);
}
bool compb(node x, node y) {
    if(x.site < y.site)return(true);
    else return(false);
}

int find(int x) {
    if(fa[x] == x) return(x);
    else {
        fa[x] = find(fa[x]);
        return(fa[x]);
    }
}//寻找祖先 
int main() {
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= m; i++) {
        tot++; scanf("%d", &a[tot].num); a[tot].site = tot; a[tot].num--;//l - 1
        tot++; scanf("%d", &a[tot].num); a[tot].site = tot;//r
        scanf("%s", s + 1);
        if(s[1] == 'e') e[i] = 0;
        else e[i] = 1;
    }
    sort(a + 1, a + tot + 1, compa);
    a[0].num = a[1].num - 1;
    for(int i = 1; i <= tot; i++) {
        if(a[i].num > a[i - 1].num) rankk++;
        a[i].rank = rankk;
    }//离散化 
    sort(a + 1, a + tot + 1, compb);

    for(int i = 1; i <= 2 * rankk; i++) fa[i] = i;//初始化 
    //fa[i]表示sum[i]是奇数, fa[i + rankk]表示sum[i]是偶数 

    for(int i = 1; i <= m; i++) {
        x = a[i * 2 - 1].rank; y = a[i * 2].rank;

        if(e[i] == 0) {//奇偶性相同 
            fax = find(x); fay = find(y + rankk);//看之前是否相反 
            if(fax == fay) {
                printf("%d\n", i - 1);
                exit(0);
            }
            fax = find(x); fay = find(y);
            if(fax != fay) {
                fa[fax] = fay;
            }
            fax = find(x + rankk); fay = find(y + rankk);
            if(fax != fay) {
                fa[fax] = fay;
            }
            //添加两条边 
        }
        else {//奇偶性相反 
            fax = find(x); fay = find(y);//看之前是否相同 
            if(fax == fay) {
                printf("%d\n", i - 1);
                exit(0);
            }
            fax = find(x); fay = find(y + rankk);
            if(fax != fay) {
                fa[fax] = fay;
            }
            fax = find(x + rankk); fay = find(y);
            if(fax != fay) {
                fa[fax] = fay;
            }
            //添加两条边 
        }

    }
    printf("%d\n", m);
    return 0;
} 

结语

通过这篇BLOG，相信你已经对并查集——这个熟悉的算法有了一点新的认识。最后希望你喜欢这篇BLOG！